Javaで二分探索を実装する基本的な方法（コード付き）

この記事の内容は Java での二分探索の基本的な実装方法 (コード付き) です。必要な方は参考にしていただければ幸いです。

二分探索は、毎回中央の数値とターゲットの数値を比較して決定する、クイック ソートとマージで使用される分割統治の考え方に似ています。それが大きいか小さいかで、間隔は半分になります。

例:

シャオ ホンが 1 ～ 100 の数字を選択し (この数字は 56)、シャオ ミンに推測するように依頼すると、次のダイアログが表示されます:

シャオ明 最初の推測: 68

シャオホン: 大きすぎます

シャオ ミンの 2 番目の推測: 35

シャオホン: 小さすぎます

シャオ ミンの 3 番目の推測 最初の推測: 58

Xiaohong: 大きすぎます

Xiao Ming の 4 番目の推測: 49

Xiaohong: 小さすぎる

Xiao Ming の 5 番目の推測 :54

小红：小红

シャオミンの 6 番目の推測: 56

小红: ビンゴ! ！ ！

上記の会話では、Xiao Ming が正解するまで推測するたびに範囲を狭めることができることがわかります。

たとえば、配列 8 は次のようになります。 、 11、 19 、 23、 27、 33、 45、 55、 67、 98 の場合は、以下に示すように二分探索を使用します。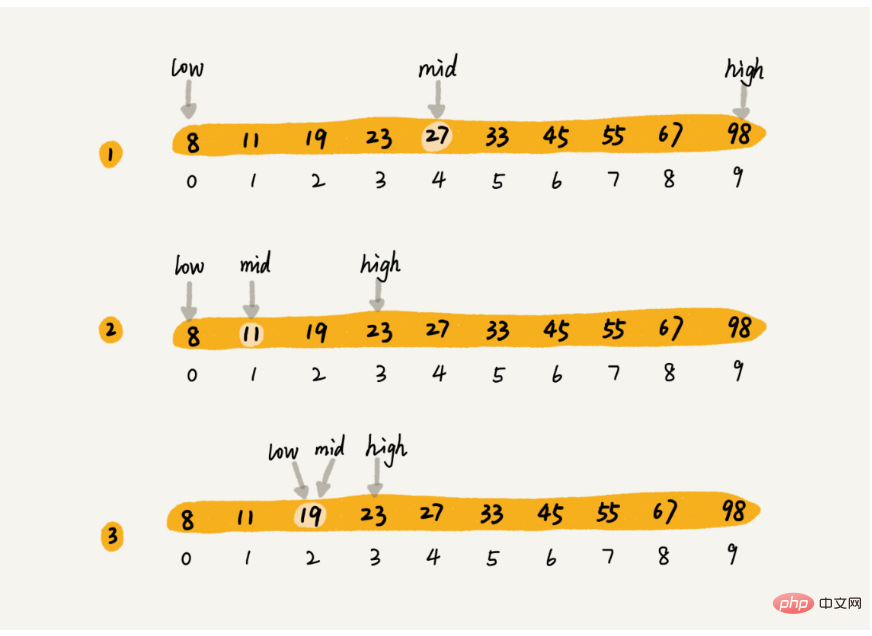

間隔を半分に減らすことができるたびに、間隔は次のように変化します。

間隔サイズが 1 に限りなく近い場合、k = log2n となるため、時間計算量は O(logn) になります。

特に理解しやすいでしょうか? 以下は、私が Java で実装した単純な二分探索です (注: これは最も単純な実装ですが、二分探索のバリエーションは非常に複雑で、私はまだ使いこなしていません)

package com.structure.search;

/**
 * 二分查找法
 *
 * @author zhangxingrui
 * @create 2019-02-15 21:29
 **/
public class BinarySearch {

    public static void main(String[] args) {
        int[] nums = new int[]{4, 6, 9, 19, 30, 40, 500, 3450, 50004, 4334343};
        System.out.println(binarySearch(nums, 0, nums.length - 1, 30));
        System.out.println(binarySearch(nums, 50004));
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-递归方式实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int p, int r, int k){
        if(p > r)
            return -1;

        int mid = (p + r) / 2;
        if(nums[mid] == k)
            return mid;

        if(k > nums[mid])
            return binarySearch(nums, mid + 1, r, k);
        else
            return binarySearch(nums, p,  mid - 1, k);
    }

    /**
     * @Author: xingrui
     * @Description: 二分查找法（针对有序数组且不存在重复元素-循环实现）
     * @Date: 21:37 2019/2/15
     */
    private static int binarySearch(int[] nums, int k){
        int p = 0;
        int r = nums.length - 1;
        while (p <= r){
            int mid = (p + r) / 2;

            if(nums[mid] == k)
                return mid;

            if(k > nums[p])
                p = mid + 1;
            else
                r = mid - 1;
        }
        return -1;
    }

}

コードは非常に単純ですが、注意する必要があるのは境界条件 p<=r です。

コードからも、単純な実装には大きな制限があり、重複データのない順序付けされた配列にのみ適用できることがわかります。

そして、二分探索は小規模なデータ クエリには適していません (小規模なデータ クエリが必要ないため)。これは理解しやすいですが、同時に大規模なデータにも適していません。質問、なぜこれが毛織物なのでしょうか？

これは、上記の理由によるものです。二分探索は、配列を使用する基になるデータに適していますが、配列は連続したメモリ空間であるため、データが大きい場合は、二分探索を使用する必要があります。データの実装 Just

配列しか使用できませんが、これはあまり良くありません。私のデータにGがあるとすると、1Gの連続メモリ空間を申請しなければなりません。ああ、もういっぱいになってしまいそうです。

以上がJavaで二分探索を実装する基本的な方法（コード付き）の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。