主要メーカーからの典型的なフロントエンド面接の質問のセレクション (回答付き)

[関連する推奨事項: フロントエンドのインタビューの質問(2020)]
1. React を書く理由/Vue プロジェクト コンポーネントにキーを書き込む機能は何ですか?
key の機能は、diff アルゴリズムの実行時に対応するノードをより速く見つけ、diff 速度を向上させることです。
Vue と React はどちらも diff アルゴリズムを使用して古い仮想ノードと新しい仮想ノードを比較し、ノードを更新します。 vue の diff 関数内。まず diff アルゴリズムを理解することができます。
相互比較中に、新しいノードと古いノードの間で相互比較の結果がない場合、古いノード配列内のキーが新しいノードのキーに従って比較され、対応する古いノードが検索されます。ノード (ここで対応するのは、キー => インデックスを持つマップです)。見つからない場合は、新しいノードとみなされます。キーがない場合は、トラバーサル検索メソッドを使用して、対応する古いノードが検索されます。 1 つはマップ マッピング、もう 1 つは横断検索です。比較において。マップマッピングが高速になります。
vue のソースコードの一部は次のとおりです:
// vue 项目 src/core/vdom/patch.js -488 行
// oldCh 是一个旧虚拟节点数组,
if (isUndef(oldKeyToIdx)) oldKeyToIdx = createKeyToOldIdx(oldCh, oldStartIdx, oldEndIdx)
idxInOld = isDef(newStartVnode.key)
? oldKeyToIdx[newStartVnode.key]
: findIdxInOld(newStartVnode, oldCh, oldStartIdx, oldEndIdx)マップ関数の作成:
function createKeyToOldIdx (children, beginIdx, endIdx) {
let i, key
const map = {}
for (i = beginIdx; i <= endIdx; ++i) {
key = children[i].key
if (isDef(key)) map[key] = i
}
return map
}トラバースして検索:
// sameVnode 是对比新旧节点是否相同的函数
function findIdxInOld (node, oldCh, start, end) {
for (let i = start; i < end; i++) {
const c = oldCh[i]
if (isDef(c) && sameVnode(node, c)) return i
}
}2. Parse ['1', '2', '3'].map(parseInt)
初見 この質問に関して私の頭に浮かぶ答えは [1, 2, 3] ですが、本当の答えは [1, NaN, NaN] です。
まず、map 関数の最初のパラメーター コールバックを確認してみましょう。
var new_array = arr.map(function callback(currentValue[, index[, array]]) { // Return element for new_array }[, thisArg])このコールバックは合計 3 つのパラメーターを受け取ることができます。最初のパラメーターは現在処理されている要素を表し、2 番目のパラメーターは要素のインデックス。
そして、parseInt は文字列を解析するために使用され、文字列を指定された基数を持つ整数にします。
parseInt(string, radix) は 2 つのパラメータを受け取ります。1 つ目は処理される値 (文字列) を表し、2 つ目は解析中の基数を表します。
これら 2 つの関数を理解した後、操作状況をシミュレーションできます;
parseInt('1', 0) //基数が 0 で、文字列パラメーターが次で終わらない場合「0x」、「0」で始まる場合は10を基準に処理します。このとき、1 が返されます;
parseInt('2', 1) // 基数 1 (基数 1) で表される数値のうち、最大値が 2 未満であるため解析できません。 NaN が返される;
parseInt('3', 2) // 基数 2 (バイナリ) で表される数値のうち、最大値が 3 未満であるため解析できず、NaN が返されます。
map 関数は配列を返すため、最終結果は [1, NaN, NaN] になります。
3. 手ぶれ補正とスロットリングとは何ですか?違いは何ですか?どのように達成するか?
1) アンチシェイク
この関数は、高頻度イベントがトリガーされた後、n 秒以内に 1 回だけ実行されます。 n 秒以内に高頻度イベントが再度発生すると、時間が再計算されます。
アイデア:
イベントがトリガーされるたびに、前の遅延呼び出しメソッドをキャンセルします:
function debounce(fn) {
let timeout = null; // 创建一个标记用来存放定时器的返回值
return function () {
clearTimeout(timeout); // 每当用户输入的时候把前一个 setTimeout clear 掉
timeout = setTimeout(() => { // 然后又创建一个新的 setTimeout, 这样就能保证输入字符后的 interval 间隔内如果还有字符输入的话,就不会执行 fn 函数
fn.apply(this, arguments);
}, 500);
};
}
function sayHi() {
console.log('防抖成功');
}
var inp = document.getElementById('inp');
inp.addEventListener('input', debounce(sayHi)); // 防抖2) スロットル
高頻度のイベントがトリガーされますが、n 秒以内に 1 回しか実行されないため、スロットリングにより関数の実行頻度が低くなります。
アイデア:
イベントがトリガーされるたびに、実行を待っている遅延関数があるかどうかが判断されます。
function throttle(fn) {
let canRun = true; // 通过闭包保存一个标记
return function () {
if (!canRun) return; // 在函数开头判断标记是否为 true,不为 true 则 return
canRun = false; // 立即设置为 false
setTimeout(() => { // 将外部传入的函数的执行放在 setTimeout 中
fn.apply(this, arguments);
// 最后在 setTimeout 执行完毕后再把标记设置为 true(关键) 表示可以执行下一次循环了。当定时器没有执行的时候标记永远是 false,在开头被 return 掉
canRun = true;
}, 500);
};
}
function sayHi(e) {
console.log(e.target.innerWidth, e.target.innerHeight);
}
window.addEventListener('resize', throttle(sayHi));4. Set、Map、WeakSet、WeakMap の違いを紹介します。
1)Set
メンバーは一意で、順序付けされておらず、繰り返しもありません。
[値、値]、キー。 value キー名と一致します (またはキー名なしでキー値のみ)。メソッドは add、delete、および has です。
2)WeakSetメンバーはすべてオブジェクトであり、
メンバーはすべて弱参照であり、ガベージ コレクション メカニズムによってリサイクルでき、使用できます。 DOM ノードを保存する場合、メモリ リークを引き起こすのは簡単ではありません。
を通過することはできず、メソッドには add、delete、has が含まれます。
3)Mapは本質的にキーと値のペアのコレクションであり、コレクションと同様に走査でき、多くのメソッドがあります。さまざまなデータ形式の変換に関連付けることができます。
4)WeakMapオブジェクトのみをキー名として受け入れます (null を除く)。他のタイプの値はキー名として受け入れません。 ##キー名 キー値は任意です。現時点では、キー名は無効です。メソッドには、get、set、has、および delete が含まれます。
5. 深さ優先トラバーサルと幅優先トラバーサルを紹介し、その実装方法を教えてください。
深さ優先探索 (DFS)深さ優先探索は、ツリーのノードを探索する一種の検索アルゴリズムです。木の枝をできるだけ深く探して、木の深さまで。ノード v のすべてのエッジが探索されると、ノード v が見つかったエッジの開始ノードまでバックトラックが実行されます。このプロセスは、ソース ノードから他のすべてのノードが探索されるまで続行されます。未検出のノードがまだある場合は、未検出のノードの 1 つをソース ノードとして選択し、すべてのノードが探索されるまで上記の操作を繰り返します。 简单的说,DFS 就是从图中的一个节点开始追溯,直到最后一个节点,然后回溯,继续追溯下一条路径,直到到达所有的节点,如此往复,直到没有路径为止。 DFS 可以产生相应图的拓扑排序表,利用拓扑排序表可以解决很多问题,例如最大路径问题。一般用堆数据结构来辅助实现 DFS 算法。 注意:深度 DFS 属于盲目搜索,无法保证搜索到的路径为最短路径,也不是在搜索特定的路径,而是通过搜索来查看图中有哪些路径可以选择。 步骤: 访问顶点 v; 依次从 v 的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和 v 有路径相通的顶点都被访问; 若此时途中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到所有顶点均被访问过为止。 实现: 测试: 测试成功。 广度优先遍历(BFS) 广度优先遍历(Breadth-First-Search)是从根节点开始,沿着图的宽度遍历节点,如果所有节点均被访问过,则算法终止,BFS 同样属于盲目搜索,一般用队列数据结构来辅助实现 BFS。 BFS 从一个节点开始,尝试访问尽可能靠近它的目标节点。本质上这种遍历在图上是逐层移动的,首先检查最靠近第一个节点的层,再逐渐向下移动到离起始节点最远的层。 步骤: 创建一个队列,并将开始节点放入队列中; 若队列非空,则从队列中取出第一个节点,并检测它是否为目标节点; 若是目标节点,则结束搜寻,并返回结果; 若不是,则将它所有没有被检测过的字节点都加入队列中; 若队列为空,表示图中并没有目标节点,则结束遍历。 实现: 测试: 测试成功。 6. 异步笔试题 请写出下面代码的运行结果: 题目的本质,就是考察setTimeout、promise、async await的实现及执行顺序,以及 JS 的事件循环的相关问题。 答案: 7. 将数组扁平化并去除其中重复数据,最终得到一个升序且不重复的数组 8.JS 异步解决方案的发展历程以及优缺点。 1)回调函数(callback) 缺点:回调地狱,不能用 try catch 捕获错误,不能 return 回调地狱的根本问题在于: 缺乏顺序性: 回调地狱导致的调试困难,和大脑的思维方式不符; 嵌套函数存在耦合性,一旦有所改动,就会牵一发而动全身,即(控制反转); 嵌套函数过多的多话,很难处理错误。 优点:解决了同步的问题(只要有一个任务耗时很长,后面的任务都必须排队等着,会拖延整个程序的执行)。 2)Promise Promise 就是为了解决 callback 的问题而产生的。 Promise 实现了链式调用,也就是说每次 then 后返回的都是一个全新 Promise,如果我们在 then 中 return ,return 的结果会被 Promise.resolve() 包装。 优点:解决了回调地狱的问题。 缺点:无法取消 Promise ,错误需要通过回调函数来捕获。 3)Generator 特点:可以控制函数的执行,可以配合 co 函数库使用。 4)Async/await async、await 是异步的终极解决方案。 优点是:代码清晰,不用像 Promise 写一大堆 then 链,处理了回调地狱的问题; 缺点:await 将异步代码改造成同步代码,如果多个异步操作没有依赖性而使用 await 会导致性能上的降低。 下面来看一个使用 await 的例子: 对于以上代码你可能会有疑惑,让我来解释下原因: 首先函数 b 先执行,在执行到 await 10 之前变量 a 还是 0,因为 await 内部实现了 generator ,generator 会保留堆栈中东西,所以这时候 a = 0 被保存了下来; 因为 await 是异步操作,后来的表达式不返回 Promise 的话,就会包装成 Promise.reslove(返回值),然后会去执行函数外的同步代码; 同步代码执行完毕后开始执行异步代码,将保存下来的值拿出来使用,这时候 a = 0 + 10。 上記の説明では、await が内部でジェネレーターを実装していると述べましたが、実際には、await はジェネレーターの構文糖に Promise を加えたもので、内部でジェネレーターの自動実行を実装しています。 co に精通している場合は、そのような糖衣構文を実際に自分で実装できます。 9. TCP の 3 ウェイ ハンドシェイクと 4 ウェイ ウェーブについての理解について話してください Graph.prototype.dfs = function() {
var marked = []
for (var i=0; i<this.vertices.length; i++) {
if (!marked[this.vertices[i]]) {
dfsVisit(this.vertices[i])
}
}
function dfsVisit(u) {
let edges = this.edges
marked[u] = true
console.log(u)
var neighbors = edges.get(u)
for (var i=0; i<neighbors.length; i++) {
var w = neighbors[i]
if (!marked[w]) {
dfsVisit(w)
}
}
}
}graph.dfs()
// 1
// 4
// 3
// 2
// 5
Graph.prototype.bfs = function(v) {
var queue = [], marked = []
marked[v] = true
queue.push(v) // 添加到队尾
while(queue.length > 0) {
var s = queue.shift() // 从队首移除
if (this.edges.has(s)) {
console.log('visited vertex: ', s)
}
let neighbors = this.edges.get(s)
for(let i=0;i<neighbors.length;i++) {
var w = neighbors[i]
if (!marked[w]) {
marked[w] = true
queue.push(w)
}
}
}
}graph.bfs(1)
// visited vertex: 1
// visited vertex: 4
// visited vertex: 3
// visited vertex: 2
// visited vertex: 5
// 今日头条面试题
async function async1() {
console.log('async1 start')
await async2()
console.log('async1 end')
}
async function async2() {
console.log('async2')
}
console.log('script start')
setTimeout(function () {
console.log('settimeout')
})
async1()
new Promise(function (resolve) {
console.log('promise1')
resolve()
}).then(function () {
console.log('promise2')
})
console.log('script end')script start
async1 start
async2
promise1
script end
async1 end
promise2
settimeout
Array.from(new Set(arr.flat(Infinity))).sort((a,b)=>{ return a-b})setTimeout(() => {
// callback 函数体
}, 1000)ajax('XXX1', () => {
// callback 函数体
ajax('XXX2', () => {
// callback 函数体
ajax('XXX3', () => {
// callback 函数体
})
})
})ajax('XXX1')
.then(res => {
// 操作逻辑
return ajax('XXX2')
}).then(res => {
// 操作逻辑
return ajax('XXX3')
}).then(res => {
// 操作逻辑
})function *fetch() {
yield ajax('XXX1', () => {})
yield ajax('XXX2', () => {})
yield ajax('XXX3', () => {})
}
let it = fetch()
let result1 = it.next()
let result2 = it.next()
let result3 = it.next()async function test() {
// 以下代码没有依赖性的话,完全可以使用 Promise.all 的方式
// 如果有依赖性的话,其实就是解决回调地狱的例子了
await fetch('XXX1')
await fetch('XXX2')
await fetch('XXX3')
}let a = 0
let b = async () => {
a = a + await 10
console.log('2', a) // -> '2' 10
}
b()
a++
console.log('1', a) // -> '1' 1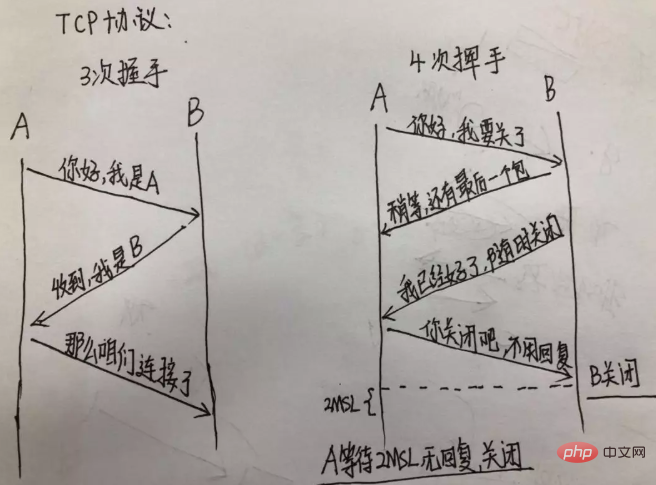

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7489
7489
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 41
41


