
Python のデータ構造とアルゴリズムの理解: Python のデータ構造はデータ要素間の関係の静的な記述を指し、アルゴリズムは問題を解決するための方法または手順を指します。言い換えれば、アルゴリズムは実際的な問題を解決するように設計されています。設計上、データ構造は、アルゴリズムが対処する必要がある問題を伝達します。
データ構造とアルゴリズムはプログラム開発者にとって必須の基礎スキルなので、率先して学び、蓄積していく必要があります。次に、この記事でこの 2 つの知識について詳しく紹介します。皆さんのお役に立てれば幸いです。

#[おすすめコース: Python チュートリアル #]
概念の紹介
最初に質問を見てみましょう:If a b c=1000, and a2 b2=c^2 (a, b, cは自然数です)、a、b、c のすべての可能な組み合わせを見つけるにはどうすればよいですか?まずは試してみましょう
import time
start_time = time.time()
# 注意是三重循环
for a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()
print("elapsed: %f" % (end_time - start_time))
print("complete!")a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 1066.117884 complete!
アルゴリズムの提案
アルゴリズムの概念
アルゴリズムはコンピュータ処理情報 コンピュータ プログラムの本質は、指定されたタスクを実行するための正確な手順をコンピュータに指示するアルゴリズムであるということです。一般に、アルゴリズムが情報を処理するとき、入力デバイスまたはデータのストレージ アドレスからデータを読み取り、後で呼び出せるように結果を出力デバイスまたはストレージ アドレスに書き込みます。アルゴリズムは、問題を解決するための独立した方法およびアイデアです。
アルゴリズムの場合、実装言語は重要ではなく、重要なのはアイデアです。
アルゴリズムにはさまざまな言語記述実装バージョン (C 記述、C 記述、Python 記述など) が存在しますが、現在は Python 言語を使用して記述および実装しています。
アルゴリズムの 5 つの特徴
入力: アルゴリズムには 0 個以上の入力があります出力: アルゴリズムには少なくとも 1 つ以上の出力があります有限性: アルゴリズムは、無限にループすることなく、限られた数のステップの後に自動的に終了し、各ステップは許容可能な時間内に完了できます。決定性: アルゴリズムの各ステップはすべて明確な意味を持ち、曖昧さはありません実現可能性: アルゴリズムのすべてのステップが実行可能です。つまり、各ステップの実行回数が制限されています2 回目の試行#
import time
start_time = time.time()
# 注意是两重循环
for a in range(0, 1001):
for b in range(0, 1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c: %d, %d, %d" % (a, b, c))
end_time = time.time()print("elapsed: %f" % (end_time - start_time))print("complete!")a, b, c: 0, 500, 500 a, b, c: 200, 375, 425 a, b, c: 375, 200, 425 a, b, c: 500, 0, 500 elapsed: 0.632128
アルゴリズム効率の測定
実行時間応答アルゴリズム効率
同じ問題に対して 2 つの解決アルゴリズムを与え、2 つのアルゴリズムの実装においてプログラムの実行時間を測定しました。2 つのプログラムの実行時間は大きく異なることがわかりました。このことから、アルゴリズム プログラムの実行時間はアルゴリズムの効率、つまりアルゴリズムの品質を反映できるという結論を導き出すことができます。時間の値だけが絶対に信頼できるのでしょうか?
古い構成でパフォーマンスが低いコンピューターでアルゴリズムの 2 回目の試行を実行したらどうなるでしょうか?おそらく、実行時間は、コンピューターでアルゴリズム 1 を実行するよりもそれほど速くはなりません。実行時間だけに基づいてアルゴリズムの長所と短所を比較することは、必ずしも客観的かつ正確であるとは限りません。
プログラムの実行は、コンピューター環境 (ハードウェアやオペレーティング システムを含む) から切り離すことはできません。これらの客観的な理由は、プログラムの実行速度に影響を与え、プログラムの実行時間に反映されます。では、アルゴリズムの品質を客観的に判断するにはどうすればよいでしょうか?時間計算量と「ビッグ O 記法」
コンピュータがアルゴリズムの各基本演算を実行するのにかかる時間は固定時間単位であると仮定します。次に、基本操作の数は、それにかかる時間単位を表します。正確な単位時間はマシン環境によって異なりますが、アルゴリズムによって実行される基本演算の数 (つまり、それにかかる時間単位の数) は桁違いに同じであるため、マシン環境の影響は次のとおりです。無視され、客観的な反応アルゴリズムの時間効率。 アルゴリズムの時間効率を高めるために、「ビッグ O 表記法」を使用してアルゴリズムを表現できます。 「ビッグ O 表記法」: 単調整数関数 f の場合、整数関数 g と実定数 c>0 が存在する場合、十分に大きな n に対して常に f(n)<; が存在します。 =c* g(n) の場合、関数 g は f (定数を無視した) の漸近関数であると言われ、 f(n)=O(g(n)) と記録されます。つまり、無限大に向かう極端な意味では、関数 f の成長率は関数 g によって制約される、つまり関数 f と関数 g の性質は似ています。 時間計算量: アルゴリズム A がサイズ n の問題例を処理するのにかかる時間が T(n)=O(g(n)) であるような関数 g があると仮定します。 O(g(n)) と呼ばれるアルゴリズム A の漸近時間計算量は時間計算量と呼ばれ、T(n) で表されます「ビッグ O 表記法」を理解する方法
对于算法进行特别具体的细致分析虽然很好,但在实践中的实际价值有限。对于算法的时间性质和空间性质,最重要的是其数量级和趋势,这些是分析算法效率的主要部分。而计量算法基本操作数量的规模函数中那些常量因子可以忽略不计。例如,可以认为3n2和100n2属于同一个量级,如果两个算法处理同样规模实例的代价分别为这两个函数,就认为它们的效率“差不多”,都为n2级。
最坏时间复杂度
分析算法时,存在几种可能的考虑:
算法完成工作最少需要多少基本操作,即最优时间复杂度
算法完成工作最多需要多少基本操作,即最坏时间复杂度
算法完成工作平均需要多少基本操作,即平均时间复杂度
对于最优时间复杂度,其价值不大,因为它没有提供什么有用信息,其反映的只是最乐观最理想的情况,没有参考价值。
对于最坏时间复杂度,提供了一种保证,表明算法在此种程度的基本操作中一定能完成工作。
对于平均时间复杂度,是对算法的一个全面评价,因此它完整全面的反映了这个算法的性质。但另一方面,这种衡量并没有保证,不是每个计算都能在这个基本操作内完成。而且,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算。
因此,我们主要关注算法的最坏情况,亦即最坏时间复杂度。
时间复杂度的几条基本计算规则
基本操作,即只有常数项,认为其时间复杂度为O(1)
顺序结构,时间复杂度按加法进行计算
循环结构,时间复杂度按乘法进行计算
分支结构,时间复杂度取最大值
判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略
在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
算法分析
第一次尝试的算法核心部分
or a in range(0, 1001):
for b in range(0, 1001):
for c in range(0, 1001):
if a**2 + b**2 == c**2 and a+b+c == 1000:
print("a, b, c: %d, %d, %d" % (a, b, c))时间复杂度:
T(n) = O(n * n * n) = O(n³)
第二次尝试的算法核心部分
for a in range(0, 1001):
for b in range(0, 1001-a):
c = 1000 - a - b
if a**2 + b**2 == c**2:
print("a, b, c: %d, %d, %d" % (a, b, c))时间复杂度:
T(n) = O(n * n * (1+1)) = O(n * n) = O(n²)
由此可见,我们尝试的第二种算法要比第一种算法的时间复杂度好多的。
常见时间复杂度
| 执行次数函数举例 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n + 3 | O(n) | 线性阶 |
| 3n² +2n + 1 | O(n²) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n³ +2n² +3n + 1 | O(n³) | 立方阶 |
| 2n | O(2n) | 指数阶 |
注意,经常将log2n(以2为底的对数)简写成logn
常见时间复杂度之间的关系
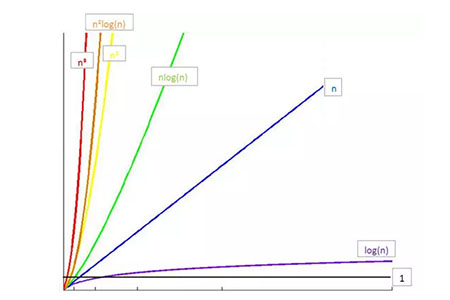
所消耗的时间从小到大
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
Python内置类型性能分析
timeit模块
timeit模块可以用来测试一小段Python代码的执行速度。
class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)
Timer是测量小段代码执行速度的类。
stmt参数是要测试的代码语句(statment)
setup参数是运行代码时需要的设置
timer参数是一个定时器函数,与平台有关。
timeit.Timer.timeit(number=1000000)
Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数,默认为1000000次。方法返回执行代码的平均耗时,一个float类型的秒数。
list的操作测试
def test1():
l = [] for i in range(1000):
l = l + [i]def test2():
l = [] for i in range(1000):
l.append(i)def test3():
l = [i for i in range(1000)]def test4():
l = list(range(1000))from timeit import Timer
t1 = Timer("test1()", "from __main__ import test1")
print("concat ",t1.timeit(number=1000), "seconds")
t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")
t3 = Timer("test3()", "from __main__ import test3")
print("comprehension ",t3.timeit(number=1000), "seconds")
t4 = Timer("test4()", "from __main__ import test4")
print("list range ",t4.timeit(number=1000), "seconds")
# ('concat ', 1.7890608310699463, 'seconds')
# ('append ', 0.13796091079711914, 'seconds')
# ('comprehension ', 0.05671119689941406, 'seconds')
# ('list range ', 0.014147043228149414, 'seconds')pop操作测试
x = range(2000000)
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = range(2000000)
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")
# ('pop_zero ', 1.9101738929748535, 'seconds')
# ('pop_end ', 0.00023603439331054688, 'seconds')测试pop操作:从结果可以看出,pop最后一个元素的效率远远高于pop第一个元素
可以自行尝试下list的append(value)和insert(0,value),即一个后面插入和一个前面插入???
list内置操作的时间复杂度

dict内置操作的时间复杂度
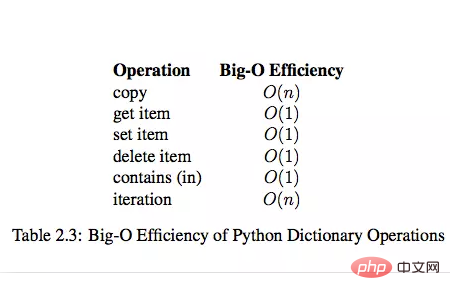
数据结构
概念
数据是一个抽象的概念,将其进行分类后得到程序设计语言中的基本类型。如:int,float,char等。数据元素之间不是独立的,存在特定的关系,这些关系便是结构。数据结构指数据对象中数据元素之间的关系。
Python给我们提供了很多现成的数据结构类型,这些系统自己定义好的,不需要我们自己去定义的数据结构叫做Python的内置数据结构,比如列表、元组、字典。而有些数据组织方式,Python系统里面没有直接定义,需要我们自己去定义实现这些数据的组织方式,这些数据组织方式称之为Python的扩展数据结构,比如栈,队列等。
算法与数据结构的区别
数据结构只是静态的描述了数据元素之间的关系。
高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法
总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
抽象数据类型(Abstract Data Type)
抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起,进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开,使它们相互独立。
最常用的数据运算有五种
插入
删除
修改
查找
排序
以上がデータ構造とアルゴリズムを理解する方法 (Python)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。