アルゴリズムの時間計算量と空間計算量
アルゴリズムの複雑さとは、アルゴリズムが実行可能プログラムに書き込まれた後、そのアルゴリズムを実行するために必要なリソースを指します。リソースには、時間リソースとメモリ リソースが含まれます。数学とコンピューティングの入門への応用。

アルゴリズムの時間計算量の定義: (推奨される学習: PHP ビデオ チュートリアル)
進行中アルゴリズム分析では、ステートメント実行の総数 T(n) は問題サイズ n の関数であり、n による T(n) の変化が分析され、T(n) の大きさのオーダーが決定されます。アルゴリズムの時間計算量、つまりアルゴリズムの時間測定値は、T(n) = O(f(n)) として記録されます。これは、問題サイズ n が増加するにつれて、アルゴリズムの実行時間の増加率が f(n) の増加率と同じになることを意味します。これは、アルゴリズムの漸近時間計算量 (時間計算量と呼ばれます) と呼ばれます。ここで、f(n) は問題サイズ n の関数です。
大文字の O() を使用して、アルゴリズムの時間計算量を反映します。これを Big O 表記法と呼びます。
さまざまなアルゴリズムでは、アルゴリズム内のステートメントの実行回数が一定であれば、時間計算量は O(1) になりますが、時間頻度が異なると時間計算量は同じになる場合もあります。たとえば、T(n)=n^2 3n 4 と T(n)=4n^2 2n 1 は周波数が異なりますが、時間計算量は同じで、どちらも O(n^2) です。
一般的な時間計算量を大きい順に並べると、次のとおりです。
定数次数 O(1)、対数次数 O(log2n) (底が 2 の n の対数、以下同じ) 、線形次数 O(n)、
線形対数次数 O(nlog2n)、二乗次数 O(n^2)、三次次数 O(n^3)、...、
k 乗次数 O(n^k)、指数次数 O(2^n)。問題サイズ n が増加し続けると、上記の時間計算量は増加し続け、アルゴリズムの実行効率は低下します。
アルゴリズム空間複雑度
時間計算量と同様に、空間複雑度は、コンピューター内でアルゴリズムが実行されるときに必要な記憶域の測定値を指します。
次のように記録されます:
S(n)=O(f(n))
アルゴリズムの実行中に必要な記憶域スペースには次のものがあります。 3 部分:
アルゴリズム プログラムが占有するスペース;
初期データ入力によって占有されるストレージ スペース;
アルゴリズムの実行中に必要な追加スペース。
多くの実際的な問題では、アルゴリズムが占有するストレージ容量を削減するために、通常、圧縮ストレージテクノロジが使用されます。
PHP 関連の技術記事の詳細については、PHP グラフィック チュートリアル 列にアクセスして学習してください。
以上がアルゴリズムの時間計算量と空間計算量の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7542
7542
 15
15
 1381
1381
 52
52
 83
83
 11
11
 21
21
 87
87
 CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
上記および筆者の個人的な理解: 現在、自動運転システム全体において、認識モジュールが重要な役割を果たしている。道路を走行する自動運転車は、認識モジュールを通じてのみ正確な認識結果を得ることができる。下流の規制および制御モジュール自動運転システムでは、タイムリーかつ正確な判断と行動決定が行われます。現在、自動運転機能を備えた自動車には通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなどのさまざまなデータ情報センサーが搭載されており、さまざまなモダリティで情報を収集して正確な認識タスクを実現しています。純粋な視覚に基づく BEV 認識アルゴリズムは、ハードウェア コストが低く導入が容易であるため、業界で好まれており、その出力結果はさまざまな下流タスクに簡単に適用できます。
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の最下層はマージ ソートを使用し、その複雑さは O(nlogn) で、クイック ソート、ヒープ ソート、安定したソートなど、さまざまなソート アルゴリズムの選択肢を提供します。
 人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能 (AI) と法執行機関の融合により、犯罪の予防と検出の新たな可能性が開かれます。人工知能の予測機能は、犯罪行為を予測するためにCrimeGPT (犯罪予測技術) などのシステムで広く使用されています。この記事では、犯罪予測における人工知能の可能性、その現在の応用、人工知能が直面する課題、およびこの技術の倫理的影響について考察します。人工知能と犯罪予測: 基本 CrimeGPT は、機械学習アルゴリズムを使用して大規模なデータセットを分析し、犯罪がいつどこで発生する可能性があるかを予測できるパターンを特定します。これらのデータセットには、過去の犯罪統計、人口統計情報、経済指標、気象パターンなどが含まれます。人間のアナリストが見逃す可能性のある傾向を特定することで、人工知能は法執行機関に力を与えることができます
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
1. マルチモーダル大型モデルの発展の歴史 上の写真は、1956 年に米国のダートマス大学で開催された最初の人工知能ワークショップです。このカンファレンスが人工知能開発の始まりとも考えられています。記号論理学の先駆者たち(前列中央の神経生物学者ピーター・ミルナーを除く)。しかし、この記号論理理論は長い間実現できず、1980 年代と 1990 年代に最初の AI の冬の到来さえもたらしました。最近の大規模な言語モデルが実装されて初めて、ニューラル ネットワークが実際にこの論理的思考を担っていることがわかりました。神経生物学者ピーター ミルナーの研究は、その後の人工ニューラル ネットワークの開発に影響を与えました。彼が参加に招待されたのはこのためです。このプロジェクトでは。
 58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
1. 58 Portraits プラットフォーム構築の背景 まず、58 Portraits プラットフォーム構築の背景についてお話ししたいと思います。 1. 従来のプロファイリング プラットフォームの従来の考え方ではもはや十分ではありません。ユーザー プロファイリング プラットフォームを構築するには、複数のビジネス分野からのデータを統合して、ユーザーの行動や関心を理解するためのデータ マイニングも必要です。最後に、ユーザー プロファイル データを効率的に保存、クエリ、共有し、プロファイル サービスを提供するためのデータ プラットフォーム機能も必要です。自社構築のビジネス プロファイリング プラットフォームとミドルオフィス プロファイリング プラットフォームの主な違いは、自社構築のプロファイリング プラットフォームは単一のビジネス ラインにサービスを提供し、オンデマンドでカスタマイズできることです。ミッドオフィス プラットフォームは複数のビジネス ラインにサービスを提供し、複雑な機能を備えていることです。モデリングを提供し、より一般的な機能を提供します。 2.58 中間プラットフォームのポートレート構築の背景のユーザーのポートレート 58
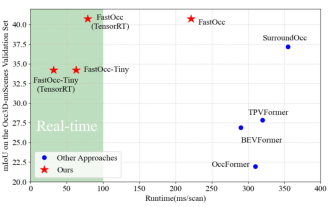 SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
上記と著者の個人的な理解は、自動運転システムにおいて、認識タスクは自動運転システム全体の重要な要素であるということです。認識タスクの主な目的は、自動運転車が道路を走行する車両、路側の歩行者、運転中に遭遇する障害物、道路上の交通標識などの周囲の環境要素を理解して認識できるようにすることで、それによって下流のシステムを支援できるようにすることです。モジュール 正しく合理的な決定と行動を行います。自動運転機能を備えた車両には、通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなど、さまざまな種類の情報収集センサーが装備されており、自動運転車が正確に認識し、認識できるようにします。周囲の環境要素を理解することで、自動運転車が自動運転中に正しい判断を下せるようになります。頭



