理解する必要がある二分木の公式

1. 一般的なバイナリ ツリーのプロパティ
プロパティ 1. 空ではないバイナリ ツリーの i レベルには、最大でも2^i ノード。
プロパティ 2. 高さ K の二分木には、最大 2^(k 1)-1 個のノードがあります。
プロパティ 3. 空ではないバイナリ ツリーの場合、葉ノードの数が n0 で、次数 2 のノードの数が n2 の場合、n0=n2 1 となります。
2, 完全なバイナリ ツリー
定義: バイナリ ツリーの場合、下位 2 レベルのノードの次数のみが 2 未満です。他のすべてのレベルのノードが 2 に等しく、最下層のノードが層の左端の位置に集中している場合、この二分木は完全二分木と呼ばれます。
プロパティ 1. n 個のノードを持つ完全な二分木の高さ k は [log^2n] です。
プロパティ 2. n 個のノードを持つ完全なバイナリ ツリーの場合、バイナリ ツリー内のすべてのノードが上 (ルート ノード) から下 (葉ノード) まで、左から右に順序付けされている場合、番号付けは 0 から始まります。
(1) i=0 の場合、それはルート ノードであり、親ノードはありません。i>0 の場合、親ノードの添え字は (i-1)/2 です。
(2) 2i 1
(3) 2i 2
3, 完全なバイナリ ツリー
定義: バイナリ ツリーのいずれかのノードがリーフであるか、空ではない 2 つのサブツリーを持つ場合、このバイナリ ツリーはフルバイナリツリーと呼ばれます。
プロパティ、完全なバイナリ ツリーでは、葉ノードの数は枝ノードの数より 1 多くなります。
4, 拡張されたバイナリ ツリー
定義: 拡張されたバイナリ ツリーは、既存のバイナリ ツリーを拡張したものです。拡張後、元のバイナリ ツリーのノードは次のようになります。次数 2 の分岐。ノード。つまり、元のノードの次数が 2 の場合はそのまま、次数が 1 の場合は 1 つの枝が追加され、次数が 0 の場合は 2 つの枝が追加されます。
プロパティ 1. 拡張バイナリ ツリーでは、外部ノードの数は内部ノードの数より 1 多くなります。
プロパティ 2. 拡張二分木では、外部パス長 E と内部パス長 I の間に次の関係が満たされます: E=I 2n (n は内部ノードの数)。
よくある質問に関連する技術的な記事については、FAQ 列を参照してください。もっと!
以上が理解する必要がある二分木の公式の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7487
7487
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 39
39
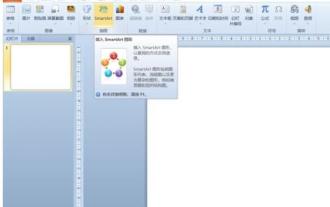 数式効果フローチャートをPPTに挿入する詳細な方法
Mar 26, 2024 pm 04:36 PM
数式効果フローチャートをPPTに挿入する詳細な方法
Mar 26, 2024 pm 04:36 PM
1. PPTを開き、[挿入]タブをクリックし、[イラスト]グループの[スマートアート]ボタンをクリックします。 2. [smartArt グラフィックの選択]ダイアログボックスが表示されるので、[処理]をクリックします。 3. 開いた[プロセス]ペインで[式]フローチャートを選択します。 4. [OK]をクリックすると、スライドペインに[数式]フローチャートが挿入されます。 5. [ここにテキストを入力] 列の [テキスト] をクリックするか、グラフィック上の [テキスト] をクリックして内容を入力します。 6. グラフィック内の図形を選択し、[smartArt ツール]の[デザイン]タブをクリックし、[グラフィックの作成]グループの[図形の追加]ボタンをクリックして図形を追加します。 7. グラフィック内の図形を選択して削除することもできますが、必要に応じて一括で削除することももちろん可能です。
 Excelの表の数式の操作方法
Mar 20, 2024 pm 12:07 PM
Excelの表の数式の操作方法
Mar 20, 2024 pm 12:07 PM
仕事でエクセルソフトを使う場合、関数式を使うことが多いですが、エクセルを使いこなせるようになりたいなら、関数式の操作に習熟する必要があります。数式をマスターするのは実はそれほど難しいことではありません。簡単な数式から学んでいきましょう。今回は Excel の表の数式の操作方法を紹介します。乗算の数式を例に、一緒に学んでいきましょう! 1. まず、Excel を開きます。ここではデモンストレーションなので、何気なく 2 つのデータを入力しました。次は、この 2 つのデータの積を計算する必要があります。列 A と列 B の積を計算し、下図の赤い丸で示すようにセルを D4 に置きます。 2. 次に、セルに等号を入力し、最初のパラメーターのセル B4 を選択し、Enter キーを押します。乗算記号を入力し、2 番目のパラメータ C4 を選択します。
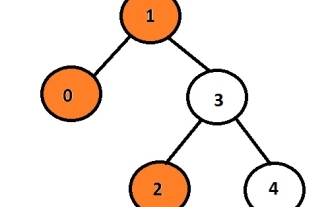 C言語でバイナリツリーの左図を印刷
Sep 03, 2023 pm 01:25 PM
C言語でバイナリツリーの左図を印刷
Sep 03, 2023 pm 01:25 PM
タスクは、指定されたバイナリ ツリーの左ノードを出力することです。まず、ユーザーはデータを挿入してバイナリ ツリーを生成し、結果のツリーの左側のビューを印刷します。各ノードは最大 2 つの子ノードを持つことができるため、このプログラムはノードに関連付けられた左ポインタのみを反復する必要があります。左ポインタが null でない場合は、それに関連付けられたデータまたはポインタがあることを意味します。それ以外の場合は、次のように出力および表示されます。出力の左側の子。例入力:10324出力:102ここで、オレンジ色のノードはバイナリ ツリーの左側のビューを表します。指定されたグラフでは、データ 1 を持つノードがルート ノードであるため、それが出力され、左の子に進む代わりに 0 が出力され、次に 3 に進み、その左の子である 2 が出力されます。再帰的メソッドを使用してノードのレベルを保存できます
 Javaのバイナリツリー構造を詳しく解説
Jun 16, 2023 am 08:58 AM
Javaのバイナリツリー構造を詳しく解説
Jun 16, 2023 am 08:58 AM
バイナリ ツリーは、コンピュータ サイエンスにおける一般的なデータ構造であり、Java プログラミングでも一般的に使用されるデータ構造です。この記事ではJavaのバイナリツリー構造について詳しく紹介します。 1. 二分木とは何ですか?コンピューター サイエンスにおけるバイナリ ツリーは、各ノードが最大 2 つの子ノードを持つツリー構造です。このうち、左側の子ノードは親ノードより小さく、右側の子ノードは親ノードより大きい。 Java プログラミングでは、ソート、検索、およびデータ クエリの効率向上を表すためにバイナリ ツリーが一般的に使用されます。 2. Java でのバイナリ ツリーの実装 Java では、バイナリ ツリー
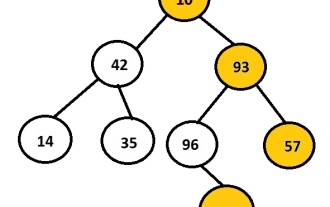 C 言語でバイナリ ツリーの右側のビューを出力します。
Sep 16, 2023 pm 11:13 PM
C 言語でバイナリ ツリーの右側のビューを出力します。
Sep 16, 2023 pm 11:13 PM
タスクは、指定されたバイナリ ツリーの右ノードを出力することです。まずユーザーはデータを挿入してバイナリ ツリーを作成し、次に結果のツリーの右側のビューを印刷します。上の画像は、ノード 10、42、93、14、35、96、57、88 を使用して作成されたバイナリ ツリーを示しており、ツリーの右側のノードが選択されて表示されています。たとえば、10、93、57、および 88 はバイナリ ツリーの右端のノードです。例 入力:1042931435965788出力:10935788 各ノードには、左ポインターと右ポインターの 2 つのポインターがあります。この質問によると、プログラムは正しいノードをトラバースするだけで済みます。したがって、ノードの左側の子を考慮する必要はありません。右側のビューには、階層内の最後のノードであるすべてのノードが保存されます。したがって、できることは、
 Python を使用してバイナリ ツリー トラバーサルを実装する方法
Jun 09, 2023 pm 09:12 PM
Python を使用してバイナリ ツリー トラバーサルを実装する方法
Jun 09, 2023 pm 09:12 PM
一般的に使用されるデータ構造として、バイナリ ツリーはデータの保存、検索、並べ替えによく使用されます。バイナリ ツリーの走査は、非常に一般的な操作の 1 つです。シンプルで使いやすいプログラミング言語である Python には、バイナリ ツリー トラバーサルを実装するためのメソッドが多数あります。この記事では、Python を使用してバイナリ ツリーの事前順序、順序内、および順序後の走査を実装する方法を紹介します。バイナリ ツリーの基本 バイナリ ツリーの探索方法を学ぶ前に、バイナリ ツリーの基本概念を理解する必要があります。バイナリ ツリーはノードで構成され、各ノードには値と 2 つの子ノード (左の子ノードと右の子ノード) があります。
 数式vlookupの使い方
Feb 19, 2024 pm 10:37 PM
数式vlookupの使い方
Feb 19, 2024 pm 10:37 PM
数式 VLOOKUP は Microsoft Excel で非常によく使用される関数で、テーブルまたはデータ セット内の特定の値を検索し、それに関連付けられた他の値を返すために使用されます。この記事では、VLOOKUP 数式の正しい使い方を学びます。 VLOOKUP 関数の基本構文は次のとおりです。 VLOOKUP(lookup_value, table_array,col_index_num, [range_lookup]) ここで、lookup
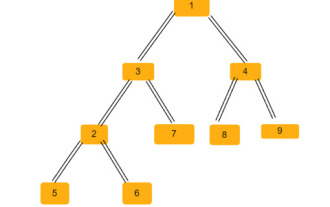 二分木内の二等辺三角形の数
Sep 05, 2023 am 09:41 AM
二分木内の二等辺三角形の数
Sep 05, 2023 am 09:41 AM
バイナリ ツリーは、各ノードが最大 2 つの子ノードを持つことができるデータ構造です。これらの子は、それぞれ左の子と右の子と呼ばれます。親の配列表現が与えられたとします。それを使用してバイナリ ツリーを作成する必要があります。二分木には複数の二等辺三角形が含まれる場合があります。この二分木で可能な二等辺三角形の総数を見つけなければなりません。この記事では、C++ でこの問題を解決するためのいくつかの手法を検討します。問題を理解すると、親配列が得られます。配列インデックスがツリー ノードの値を形成し、配列内の値がその特定のインデックスの親ノードを与えるように、それをバイナリ ツリーの形式で表す必要があります。 -1 は常にルートの親であることに注意してください。以下に、配列とそのバイナリ ツリー表現を示します。親配列=[0,-1,3,1,



