二重浮動小数点演算の精度が低下するのはなぜですか?

まえがき: 仕事で、小数点を使った加減乗除の計算になると、BigDecimal を使って解決しようと考えますが、多くの人はその理由について混乱しています。 double または float は精度を失います。 BigDecimal を解決するにはどうすればよいでしょうか?さっそく始めましょう。
1. 浮動小数点数とは何ですか?
浮動小数点数は、コンピューターが科学表記法を使用して小数を表すために使用するデータ型です。 Java では、double は倍精度、64 ビット、浮動小数点数であり、デフォルトは 0.0d です。 float は単精度、32 ビットです。浮動小数点数、デフォルトは 0.0f;

メモリに格納
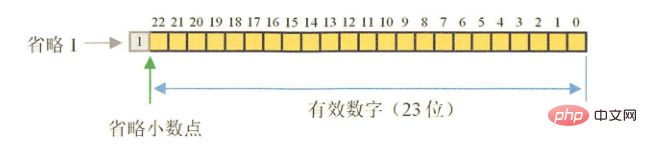
float 符号ビット (1 ビット) 指数 ( 8 ビット) 仮数部 (23 ビット)
double Sign ビット (1 ビット) 指数部 (11 ビット) 仮数部 (52 ビット)
メモリ内の浮動小数点の指数は、実際には指数であるため 8 ビットです。指数のフレームシフトの場合、指数の真の値が e で順序コードが E であると仮定すると、E=e (2^n-1 -1) となります。このうち、2^n-1 -1 は IEEE754 規格で規定されている指数オフセットであり、この式によれば 2^8 -1=127 となります。したがって、float の指数範囲は -128 127 ですが、double の指数範囲は -1024 1023 です。負の指数は浮動小数点数で表現できる最小の絶対値を持つ非ゼロの数値を決定し、正の指数は浮動小数点数で表現できる最大の絶対値を持つ数値を決定し、値の範囲も決定します。浮動小数点数の。
float の範囲は -2^128 ~ 2^127、つまり -3.40E 38 ~ 3.40E 38;
double の範囲は -2^1024 ~ 2^ 1023、また、それは -1.79E 308 ~ 1.79E 308
2. 歪みの科学的記数法を入力します
まず科学的記数法について話しましょう. 科学的記数法は、カウントを簡素化する方法です。非常に大きな数値または小さな数値を桁数の多い値で近似的に表現する場合、桁数の少ない値には科学的表記法の利点はありませんが、桁数の多い値については数え方の利点が得られます。は非常に明白です。たとえば、光の速度は 300000000 メートル/秒、世界の人口は約 6100000000 人です。光の速度や世界の人口のような大きな数値は読み書きに不便なので、光の速度は 3*10^8 として記述でき、世界の人口は 6.1*10^9 として記述できます。したがって、計算機は科学表記法を使用して、光の速度が 3E8 で、世界の人口が約 6.1E9 であることを示します。
私たちは子供の頃、狂ったように足したり引いたりするのが好きで電卓で遊んでいたのですが、最終的には電卓は下の図を表示しました。これは科学的表記法で表示された結果です。
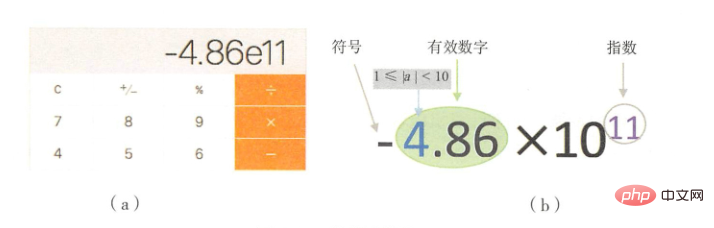
#画像内の実際の値は -4.86*10^11=-486000000000 です。 10 進科学表記法では、有効数字の整数部分が [1, 9] の範囲内にある必要があります。
3. 歪みの精度を理解する
コンピューターがデータを処理する際には、データ変換や、さまざまな単位やさまざまな基数の変換など、さまざまな複雑な操作が必要になります。 (2進数10進数など)変換など、10÷3=3.3333…無限など割り算できない割り算が多く、精度に限界がある、3.3333333x3が複雑な処理後の小数である10に等しくないデータは正確ではありませんが、精度が高いほど正確になります。 float と double の精度は仮数部の桁数によって決まります。整数部分は常に暗黙の "1" であり、変更されないため、精度に影響を与えることはありません。 float: 2^23 = 8388608 計7桁 左端の桁が省略されているので、28388608 = 16777216 と8桁まで表現できることになります。有効数字は 8 桁ですが、必ず 7 桁であることが保証されており、float の精度は有効数字 7 ~ 8 桁、double: 2^52 = 4503599627370496 の合計 16 桁、同様に double の精度は16~17ビットです。
特定の値に達すると、科学表記法の使用が自動的に開始され、関連する精度の有効数字が保持されるため、結果は近似値となり、指数は整数になります。 10 進数では、一部の 10 進数は 2 進数で完全に表現できません。したがって、限られたビットでしか表現できないため、保存時にエラーが発生する可能性があります。 10 進数を 2 進数に変換するには、2 倍の方法を使用して計算し、整数部分を削除した後、小数部分がすべて 0 になるまで残りの小数を 2 倍します。

0.3 * 2 = 0.6 => .0 (.6) で 0.3 をバイナリに変換し、0 を取り、0.6
0.6 * 2 = 1.2 => を残す必要があります。 .01 (. 2) 1 を取り、0.2
0.2 * 2 = 0.4 => .010 (.4) 0 を取り、0.4
0.4 * 2 = 0.8 => .0100 (.8) 0 を取り、0.8## を残します #0.8 * 2 = 1.6 => .01001 (.6) は 1 を取り、0.6 を残します
....

3. 概要
上記を読めば、浮動小数点数に精度の問題がある理由がおそらく明らかになるでしょう。簡単に言うと、float 型と double 型は主に科学計算と工学計算用に設計されており、広範囲の値に対してより正確かつ高速な近似和計算を提供するように慎重に設計された 2 進浮動小数点演算を実行します。ただし、完全に正確な結果が得られるわけではないため、正確な結果を得るために使用しないでください。特定のサイズに達した浮動小数点数は科学表記法を自動的に使用しますが、このような表現は実数の近似にすぎず、実数と同じではありません。 10 進数を 2 進数に変換するときに、無限ループや浮動小数点の仮数の長さの超過も発生する可能性があります。
4. では、BigDecimal を使用してそれを解決するにはどうすればよいでしょうか?
以下の 2 つの出力を見てください

0.3
以上が二重浮動小数点演算の精度が低下するのはなぜですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7694
7694
 15
15
 1640
1640
 14
14
 1393
1393
 52
52
 1287
1287
 25
25
 1229
1229
 29
29
 PHPで文字列を10進数に変換する方法
Mar 22, 2023 pm 03:22 PM
PHPで文字列を10進数に変換する方法
Mar 22, 2023 pm 03:22 PM
PHP は、Web 開発の分野で広く使用されている強力なプログラミング言語です。非常に一般的な状況の 1 つは、文字列を 10 進数に変換する必要があることです。これはデータ処理を行うときに非常に便利です。この記事では、PHPで文字列を10進数に変換する方法を説明します。
 PHPの浮動小数点数の丸め方法
Mar 21, 2024 am 09:21 AM
PHPの浮動小数点数の丸め方法
Mar 21, 2024 am 09:21 AM
この記事では、PHP の浮動小数点数の四捨五入方法について詳しく解説しますが、非常に実践的だと編集者が考えたので、参考として共有しますので、この記事を読んで何かを得ることができれば幸いです。 PHP 浮動小数点丸めの概要 コンピュータでは、浮動小数点数は小数点とそれに続く指数として表されますが、多くの場合、限られた桁数の近似値で格納されます。浮動小数点数を特定の精度に丸める必要がある場合、それを行う方法がいくつかあります。方法 1.round() 関数round() 関数は、浮動小数点数を最も近い整数に丸めます。浮動小数点数とオプションの精度パラメータを受け入れます。例: $num=1.55;echoround($num);//出力: 2echoround($num,1)
 strconv.FormatFloat 関数を使用して浮動小数点数を文字列に変換します
Jul 25, 2023 am 11:45 AM
strconv.FormatFloat 関数を使用して浮動小数点数を文字列に変換します
Jul 25, 2023 am 11:45 AM
strconv.FormatFloat 関数を使用して、浮動小数点数を文字列に変換します。Go 言語では、出力またはストレージのニーズに応じて、浮動小数点数を文字列型に変換する必要がよくあります。 strconv パッケージは Go 言語で提供されており、その中の FormatFloat 関数は浮動小数点数を文字列型に変換できます。 FormatFloat 関数は 3 つのパラメータを取ります。f は変換される浮動小数点数を表し、fmt は形式を表し、prec は保持する小数点以下の桁数を表します。このうち、fパラメータは
 double型変数をint型に変換するC++プログラム
Aug 25, 2023 pm 08:25 PM
double型変数をint型に変換するC++プログラム
Aug 25, 2023 pm 08:25 PM
C++ では、int 型の変数は正または負の整数値のみを保持でき、10 進数値を保持できません。この目的に使用できる float 値と double 値があります。 double データ型は、小数点以下 7 桁までの小数を格納するために作成されました。整数から double データ型への変換は、コンパイラによって自動的に実行することも (「暗黙的」変換と呼ばれます)、プログラマがコンパイラに明示的に要求することもできます (「明示的」変換と呼ばれます)。次のセクションでは、さまざまな変換方法について説明します。暗黙的な変換 コンパイラは暗黙的な型変換を自動的に実行します。これを実現するには、浮動小数点型と整数型の 2 つの変数が必要です。浮動小数点値または変数を整数変数に代入するだけでは、コンパイラが他のすべてのことを処理します。
 PHP 浮動小数点計算エラーの原因と回避方法
Feb 27, 2024 pm 06:33 PM
PHP 浮動小数点計算エラーの原因と回避方法
Feb 27, 2024 pm 06:33 PM
人気のサーバーサイド スクリプト言語である PHP では、浮動小数点計算を実行するときに精度の低下や計算エラーの問題が頻繁に発生し、プログラムの精度と安定性に影響を与える可能性があります。この記事では、PHP 浮動小数点計算エラーの原因を調査し、いくつかの回避戦略を提案し、参考として具体的なコード例を示します。 1. PHP 浮動小数点計算エラーの理由 コンピューターでは、浮動小数点数は 2 進数形式で表現されますが、2 進数ではすべての 10 進数を正確に表現できないため、浮動小数点数が不正確になります。
 PHP BCMath の徹底解説: 数値演算の可能性を解き放つ
Feb 23, 2024 am 09:10 AM
PHP BCMath の徹底解説: 数値演算の可能性を解き放つ
Feb 23, 2024 am 09:10 AM
:1. BCMath の概要 BCMath は、PHP に組み込まれた拡張ライブラリであり、特に大きな整数および浮動小数点数の演算を処理するために使用されます。加算、減算、乗算、除算、平方、平方根などのさまざまな数学演算を実行するための豊富な関数を提供し、複数の基底でのデジタル表現をサポートします。 2. BCMath の利点 PHP がネイティブに提供する算術演算子や関数と比較して、BCMath には主に次の利点があります: 高精度: BCMath の演算結果はより多くの有効桁数を保持できるため、大きな数値を含む計算に役立ちます。より広い範囲: BCMath は、PHP のネイティブ データ型よりも大きな数値を処理できるため、オーバーフローや精度の低下の問題を回避できます。より豊富な機能: BCMath が提供する
 C# の Math.Round 関数を使用して浮動小数点数を丸めます
Nov 18, 2023 pm 02:17 PM
C# の Math.Round 関数を使用して浮動小数点数を丸めます
Nov 18, 2023 pm 02:17 PM
C# で Math.Round 関数を使用して浮動小数点数を丸めるには、特定のコード例が必要です。C# プログラミング言語では、浮動小数点数を丸める必要がある場合があります。現時点では、Math.Round 関数を使用してこの機能を実現できます。 Math.Round 関数は、数学的計算に使用される C# の組み込み関数であり、その主な機能は、指定された浮動小数点数を四捨五入することです。 Math.Round 関数の一般的な形式は次のとおりです。 Math.Round(doub
 PHPで文字列をfloatに変換する方法
Mar 27, 2024 pm 12:48 PM
PHPで文字列をfloatに変換する方法
Mar 27, 2024 pm 12:48 PM
文字列を浮動小数点数に変換するのは PHP の一般的な操作であり、組み込みメソッドを使用して実行できます。文字列を浮動小数点数に正常に変換するには、まず文字列が有効な浮動小数点形式であることを確認してください。以下では、PHP で文字列を浮動小数点数に変換する方法を詳しく説明し、具体的なコード例を示します。 1. (float) キャストを使用する PHP で文字列を浮動小数点数に変換する最も簡単な方法は、キャストを使用することです。強制的に変換するには、文字列の前に (float) を追加します。これにより、PHP が自動的に変換します。



