二分探索法は、要素間の順序関係を利用し、分割統治戦略を採用することで、最悪の場合でもO(log n)で探索を完了することができます。
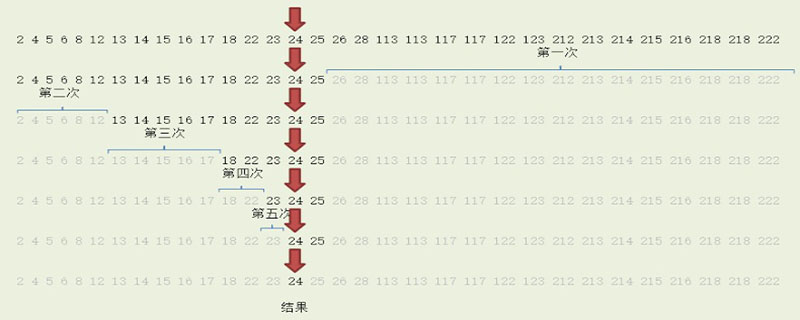
基本的な考え方は、n 個の要素をほぼ同じ数で 2 つの半分に分割し、a[n/2] と求めた数を取ることです。 x を比較し、x=a[n/2] の場合、x が見つかり、アルゴリズムの動作は終了します。 (推奨学習: web フロントエンド ビデオ チュートリアル )
コンピュータ サイエンスでは、二分探索 (英語: binary search)、または半区間探索 (英語:half) と呼ばれます。 -interval search) , 対数探索(英語: logarithmic search )とは、順序付けされた配列内の特定の要素を見つけるための検索アルゴリズムです。
検索プロセスは配列の中央の要素から開始されます。中央の要素が見つかった場合は検索プロセスが終了します。特定の要素が中央の要素より大きいか小さい場合は、配列が中央の要素より大きいか小さい場合、検索プロセスは終了します。その半分を検索し、前と同様に中央の要素から比較を開始します。
あるステップで配列が空の場合、それは見つからないことを意味します。この検索アルゴリズムでは、比較するたびに検索範囲が半分に減ります。
xa[n/2] の場合、配列 a の右半分で x の検索を続けるだけで済みます。
二分探索法は非常に広く使用されており、その考え方は理解しやすいですが、正しい二分探索アルゴリズムを記述するのは簡単ではありません。最初の二分探索アルゴリズムは 1946 年には登場しましたが、最初の完全に正しい二分探索アルゴリズムは 1962 年まで登場しませんでした。
Bentley は著書「Writing Correct Programs」の中で、コンピュータ専門家の 90% は 2 時間以内に完全に正しい二分探索アルゴリズムを書くことができないと書いています。
この問題の鍵は、各探索範囲の境界と終了条件を正確に定式化し、奇数と偶数のさまざまな状況を正しく要約することです。その特定のアルゴリズムは非常に直感的であることがわかります。
計算量の計算
時間計算量: 二分探索では毎回検索範囲が半分になります。時間計算量が O(log n) であることは明らかです。 (n はセット内の要素の数を表します)
空間計算量: O(1)。再帰的形式で定義されていますが、末尾再帰的であり、ループとして書き換えることができます。
以上が二分探索法の時間計算量の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。