Java ハッシュマップ透析

HashMap は配列とリンクリストから構成される複雑な構造です. ハッシュ値によって配列内のキー値の位置が決まります. ハッシュ値が同じ場合,リンク リストの形式で保存されます。リンク リストの長さが設定されたしきい値に達すると、ツリー化されます。これは、データのセキュリティとデータ関連の操作の効率を確保するために行われます。

HashMap のパフォーマンスはハッシュ コードの有効性に依存するため、hashCode とquals は基本的に次のようになります。合意されたルールは特に重要です。たとえば、equals は等しい、hashCode は等しい必要があります。hashCode が書き換えられた場合は、equals も書き換えられなければなりません。hashCode一貫性を維持する必要があり、ステータス変更によって返されるハッシュ値も、対称性、反映、等値の伝達など、一貫性が保たれている必要があります。 HashMap、Hashtable、TreeMap の間

#HashMap: 配列ベースの非同期ハッシュ テーブル。null キーをサポートするか、キーと値のペアのアクセス データ シナリオでは Value が最初の選択肢です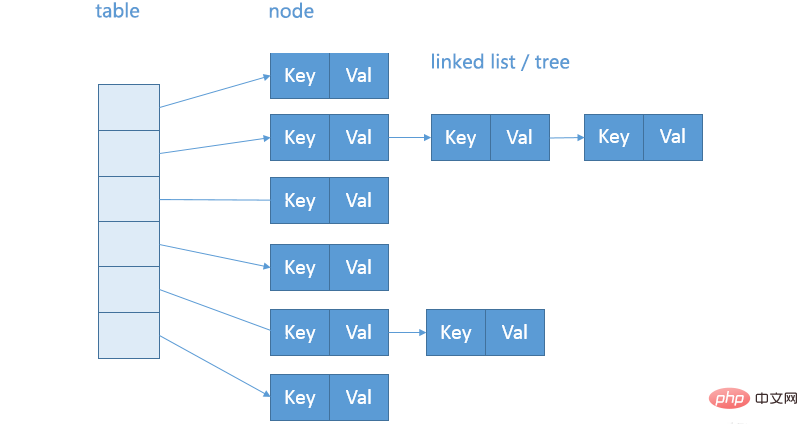

Hashtable:配列に基づく同期されたハッシュ テーブル。null キーや値はサポートされません。同期はパフォーマンスに影響を与えるため、めったに使用されません

TreeMap: 赤黒ツリーに基づいて順次アクセスを提供するマップ。 HashMap よりも空間が広くなりますが、データ操作 (チェック、追加、削除) の時間計算量は O (log (n)) であり、HashMap とは異なります。 null 値をサポートします。キーが空で Comparator インターフェイスが実装されていない場合、NullPointerException が発生します。Comparator インターフェイスを実装し、null オブジェクトを判断することで、通常のストレージを実現できます。

HashMap、Hashtable、および TreeMap はすべて使用しますキーと値のペア フォームはデータ要素を保存または操作します。 HashMap と TreeMap は AbstractMap クラスから継承し、Hashtable は Dictionary クラスから継承します。これら 3 つはすべて Map インターフェイスを実装します。

HashMap ソース コード分析

HashMap( )

public HashMap(int initialCapacity, float loadFactor){  
    // ... 
    this.loadFactor = loadFactor;
    this.threshold = tableSizeFor(initialCapacity);
}

HashMap の初期化時には一部の初期値のみが設定されますが、データの処理を開始すると、.put() メソッドが徐々に複雑になりますHashMap.put()

    public V put(K key, V value) {
        return putVal(hash(key), key, value, false, true);
    }

    final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
    	// 定义新tab数组及node对象
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        // 如果原table是空的或者未存储任何元素则需要先初始化进行tab的初始化
        if ((tab = table) == null || (n = tab.length) == 0)
            n = (tab = resize()).length;
        // 当数组中对应位置为null时，将新元素放入数组中
        if ((p = tab[i = (n - 1) & hash]) == null)
            tab[i] = newNode(hash, key, value, null);
        // 若对应位置不为空时处理哈希冲突
        else {
            Node<K,V> e; K k;
            // 1 - 普通元素判断： 更新数组中对应位置数据
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            // 2 - 红黑树判断：当p为树的节点时，向树内插入节点
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            // 3 - 链表判断：插入节点
            else {
                for (int binCount = 0; ; ++binCount) {
                	// 找到尾结点并插入
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        // 判断链表长度是否达到树化阈值，达到就对链表进行树化
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    // 更新链表中对应位置数据
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            // 如果存在这个映射就覆盖
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                // 判断是否允许覆盖，并且value是否为空
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                // 回调以允许LinkedHashMap后置操作
                afterNodeAccess(e); 
                return oldValue;
            }
        }
        // 更新修改次数
        ++modCount;
        // 检查数组是否需要进行扩容
        if (++size > threshold)
            resize();
        // 回调以允许LinkedHashMap后置操作
        afterNodeInsertion(evict);
        return null;
    }

テーブルがnullの場合はresize()で初期化されますが、resize()にはテーブルを作成して初期化する機能と、容量が足りない場合にテーブルを拡張する機能があります。需要を満たす:

        if (++size > threshold)
            resize();

特定のキー 値ペアの格納場所の計算方法は次のとおりです:

        if ((p = tab[i = (n - 1) & hash]) == null)
            // 向数组赋值新元素
            tab[i] = newNode(hash, key, value, null);
        else {
            Node<K,V> e; K k;
            // 如果新插入的结点和table中p结点的hash值，key值相同的话
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
                e = p;
            // 如果是红黑树结点的话，进行红黑树插入
            else if (p instanceof TreeNode)
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
                for (int binCount = 0; ; ++binCount) {
                    // 代表这个单链表只有一个头部结点，则直接新建一个结点即可
                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        // 链表长度大于8时，将链表转红黑树
                        if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                            treeifyBin(tab, hash);
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    // 及时更新p
                    p = e;
                }
            }
            // 如果存在这个映射就覆盖
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                // 判断是否允许覆盖，并且value是否为空
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);     // 回调以允许LinkedHashMap后置操作
                return oldValue;
            }
        }

.put() メソッドのハッシュ計算に注意してください。hashCode ではありません。ただし、XOR 演算のためにキーのハッシュコードの上位ビット データを下位ビットにシフトします。この方法では、計算されたハッシュ値の主な違いが上位ビットにあるデータは、上位ビットにあるため無視されません。 HashMap でハッシュ アドレス指定するときに容量を超えるビットを使用できるため、このような状況でのハッシュの衝突を効果的に回避できます

    static final int hash(Object key) {
        int h;
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

HashMap.resize()

    final Node<K,V>[] resize() {
    	// 把当前底层数组赋值给oldTab，为数据迁移工作做准备
        Node<K,V>[] oldTab = table;
        // 获取当前数组的大小，等于或小于0表示需要初始化数组，大于0表示需要扩容数组
        int oldCap = (oldTab == null) ? 0 : oldTab.length;
        // 获取扩容的阈值（容量*负载系数）
        int oldThr = threshold;
        // 定义并初始化新数组长度和目标阈值
        int newCap, newThr = 0;
        // 判断是初始化数组还是扩容，等于或小于0表示需要初始化数组，大于0表示需要扩容数组。若  if(oldCap > 0)=true 表示需扩容而非初始化
        if (oldCap > 0) {
        	// 判断数组长度是否已经是最大，MAXIMUM_CAPACITY =（2^30）
            if (oldCap >= MAXIMUM_CAPACITY) {
            	// 阈值设置为最大
                threshold = Integer.MAX_VALUE;
                return oldTab;
            }
            else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                     oldCap >= DEFAULT_INITIAL_CAPACITY)            	
            	// 目标阈值扩展2倍，数组长度扩展2倍
                newThr = oldThr << 1; // double threshold
        }
        // 表示需要初始化数组而不是扩容
        else if (oldThr > 0) 
        	// 说明调用的是HashMap的有参构造函数，因为无参构造函数并没有对threshold进行初始化
            newCap = oldThr;
        // 表示需要初始化数组而不是扩容，零初始阈值表示使用默认值
        else {	
        	// 说明调用的是HashMap的无参构造函数
            newCap = DEFAULT_INITIAL_CAPACITY;
            // 计算目标阈值
            newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
        }
        // 当目标阈值为0时需重新计算，公式：容量（newCap）*负载系数（loadFactor）
        if (newThr == 0) {
            float ft = (float)newCap * loadFactor;
            newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                      (int)ft : Integer.MAX_VALUE);
        }
        // 根据以上计算结果将阈值更新
        threshold = newThr;
        // 将新数组赋值给底层数组
        @SuppressWarnings({"rawtypes","unchecked"})
            Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
        table = newTab;
        
        // -------------------------------------------------------------------------------------
        // 此时已完成初始化数组或扩容数组，但原数组内的数据并未迁移至新数组（扩容后的数组），之后的代码则是完成原数组向新数组的数据迁移过程
        // -------------------------------------------------------------------------------------
        
        // 判断原数组内是否有存储数据，有的话开始迁移数据
        if (oldTab != null) {
        	// 开始循环迁移数据
            for (int j = 0; j < oldCap; ++j) {
                Node<K,V> e;
                // 将数组内此下标中的数据赋值给Node类型的变量e，并判断非空
                if ((e = oldTab[j]) != null) {
                    oldTab[j] = null;
                    // 1 - 普通元素判断：判断数组内此下标中是否只存储了一个元素，是的话表示这是一个普通元素，并开始转移
                    if (e.next == null)
                        newTab[e.hash & (newCap - 1)] = e;
                    // 2 - 红黑树判断：判断此下标内是否是一颗红黑树，是的话进行数据迁移
                    else if (e instanceof TreeNode)
                        ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                    // 3 -  链表判断：若此下标内包含的数据既不是普通元素又不是红黑树，则它只能是一个链表，进行数据转移
                    else { // preserve order
                        Node<K,V> loHead = null, loTail = null;
                        Node<K,V> hiHead = null, hiTail = null;
                        Node<K,V> next;
                        do {
                            next = e.next;
                            if ((e.hash & oldCap) == 0) {
                                if (loTail == null)
                                    loHead = e;
                                else
                                    loTail.next = e;
                                loTail = e;
                            }
                            else {
                                if (hiTail == null)
                                    hiHead = e;
                                else
                                    hiTail.next = e;
                                hiTail = e;
                            }
                        } while ((e = next) != null);
                        if (loTail != null) {
                            loTail.next = null;
                            newTab[j] = loHead;
                        }
                        if (hiTail != null) {
                            hiTail.next = null;
                            newTab[j + oldCap] = hiHead;
                        }
                    }
                }
            }
        }
        // 返回初始化完成或扩容完成的新数组
        return newTab;
    }

容量と負荷係数によってアレイの容量が決まります。スペースがあるとスペースの無駄が発生し、使いすぎると操作のパフォーマンスに影響します。事前に容量を決めておきます。容量拡張が発生する条件に基づいて具体的な値を簡単に見積もることができます。前のコード分析に基づいて、負荷率 * 容量 > 要素数

# という計算条件を満たす必要があることがわかります。 ## したがって、プリセット容量は満たす必要があり、推定要素数/負荷率より大きく、2 の累乗になります。

## ただし、次の点に注意してください:

JDK 自体のデフォルトの負荷係数は一般的なシナリオのニーズと非常に一致しているため、特別な必要がない場合は、簡単に変更を続行しないでください。本当に調整する必要がある場合は、0.75 を超える値を設定しないことをお勧めします。これは、競合が大幅に増加し、HashMap のパフォーマンスが低下するためです。負荷率が小さすぎると、設定された容量値も上記の計算式に従って調整されますが、そうでない場合、容量拡張が頻繁に行われ、不要なオーバーヘッドが増加し、アクセス性能自体にも影響が出る可能性があります。

HashMap.get()

    public V get(Object key) {
        Node<K,V> e;
        return (e = getNode(hash(key), key)) == null ? null : e.value;
    }

    final Node<K,V> getNode(int hash, Object key) {
        Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
        // 将table赋值给变量tab并判断非空 && tab 的厂部大于0 && 通过位运算得到求模结果确定链表的首节点赋值并判断非空
        if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
        	// 判断首节点hash值 && 判断key的hash值（地址相同 || equals相等）均为true则表示first即为目标节点直接返回
            if (first.hash == hash && // always check first node
                ((k = first.key) == key || (key != null && key.equals(k))))
                return first;
            // 若首节点非目标节点，且还有后续节点时，则继续向后寻找
            if ((e = first.next) != null) {
            	// 1 - 树：判断此节点是否为树的节点，是的话遍历树结构查找节点，查找结果可能为null
                if (first instanceof TreeNode)
                    return ((TreeNode<K,V>)first).getTreeNode(hash, key);
                // 2 - 链表：若此节点非树节点，说明它是链表，遍历链表查找节点，查找结果可能为null
                do {
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        return e;
                } while ((e = e.next) != null);
            }
        }
        return null;
    }

HashMap がツリー化される理由

データのセキュリティと関連する操作の効率を確保するため

要素の配置プロセス中に、オブジェクト ハッシュが競合し、同じバケットに配置された場合、リンク リストが形成されるため、リンク リスト クエリは線形であることがわかっており、アクセスのパフォーマンスに重大な影響を及ぼします

現実の世界では、ハッシュ競合データの構築はそれほど複雑な問題ではありません。悪意のあるコードは、このデータを使用してサーバー側と大量に対話し、サーバー側の CPU 使用量を大量に引き起こす可能性があります。これは、ハッシュ衝突の拒否を構成します。サービス攻撃。国内の第一線のインターネット企業でも同様の攻撃が発生しています。

以上がJava ハッシュマップ透析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。