MySQL がインデックス構造として B+ ツリーを選択するのはなぜですか? (詳しい説明)

MySQL では、Innodb と MyIsam の両方がインデックス構造として B ツリーを使用します (ハッシュなどの他のインデックスはここでは考慮されません)。この記事では、最も一般的な二分探索ツリーから始めて、さまざまなツリーによって解決される問題と直面する新たな問題を徐々に説明し、それによって MySQL がインデックス構造として B ツリーを選択する理由を説明します。

1. 二分探索木 (BST): 不均衡# #Binary Search Tree (BST、Binary Search Tree) は、バイナリソートツリーとも呼ばれ、バイナリツリーに基づいて満たす必要があります。つまり、任意のノードの左側のサブツリー上のすべてのノードの値がルートノードの値より大きくないことです。 、任意のノード 右のサブツリー内のすべてのノードの値がルート ノードの値以上です。以下はBST（ピクチャーソース）です。

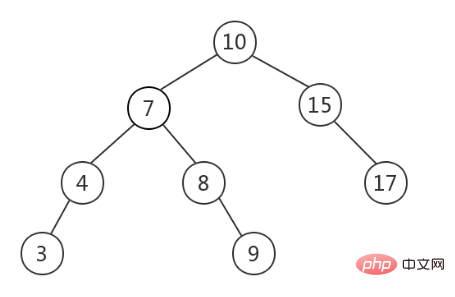高速検索が必要な場合、BST にデータを保存するのが一般的な選択です。これは、現時点ではクエリ時間はツリーの高さに依存し、平均時間計算量は O であるためです。 (lgn)。ただし、

BST

は、下の図 (画像ソース) に示すように、歪んで不均衡になる可能性があります。このとき、BST はリンク リストに縮退し、時間計算量は次のように縮退します。の上）。 この問題を解決するために、バランスのとれたバイナリ ツリーが導入されます。

2. バランス バイナリ ツリー (AVL): 回転には時間がかかります

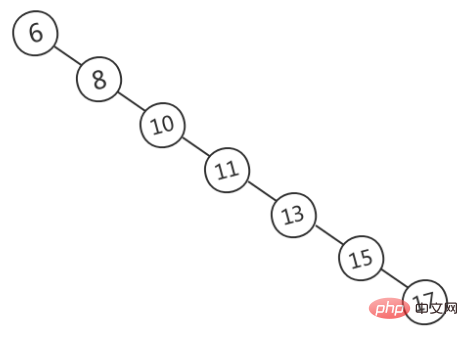
AVL ツリーは厳密にバランスが取れていますバイナリ ツリーの場合、すべてのノードの左右のサブツリー間の高さの差は 1 を超えることはできません。AVL ツリーの検索、挿入、削除は、平均と最悪の場合の両方で O(lgn) です。

AVL でバランスを実現する鍵は、回転操作にあります。挿入と削除によってバイナリ ツリーのバランスが崩れる可能性があるため、1 回以上のツリーの回転を通じてツリーのバランスを再調整する必要があります。データ挿入時はせいぜい1回転（一回転または二回転）だけで済みますが、データを削除するとツリーのバランスが崩れてしまいますので、AVLでは削除したノードからのパス上にある全ノードのバランスを保つ必要があります。ルートノードまでの回転 回転の大きさはO(lgn)です。

時間のかかるローテーションのため、AVL

ツリーはデータを削除する際に非常に非効率的です; 多数の削除操作がある場合、バランスを維持するコストが高くなる可能性があります。利益よりも高いため、AVL は実際には広く使用されていません。

3. 赤黒木: 木が高すぎる

AVL 木と比較して、赤黒木は厳密なバランスを追求していないただし、これは大まかなバランスです。ルートからリーフまでの可能な最長のパスの長さが、可能な最短のパスの 2 倍を超えないように注意してください。実装の観点から見ると、赤黒ツリーの最大の特徴は、各ノードが 2 つの色 (赤または黒) のいずれかに属しており、ノードの色の分け方は特定の規則を満たす必要があることです (特定の規則は省略します)。 。赤黒ツリーの例は次のとおりです (画像ソース):

AVL ツリーと比較すると、赤黒ツリーのクエリ効率は低下します。木のバランスが変わってしまうからで、悪くなると高さが高くなってしまいます。ただし、赤黒ツリーには色も導入されているため、赤黒ツリーの削除効率は大幅に向上しました。データの挿入または削除の際、基本的なバランスを確保するために必要な回転と色の変更は O(1) 回だけです。 AVL は必要ありません。ツリーは O(lgn) 回の回転を実行します。一般に、赤黒ツリーの統計的パフォーマンスは AVL よりも高くなります。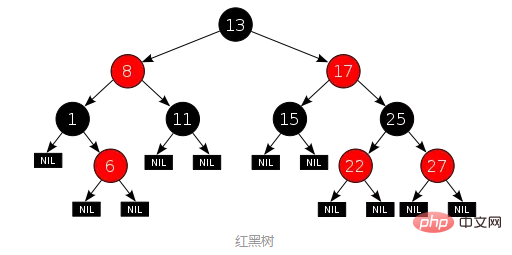

したがって、実際のアプリケーションでは、AVL ツリーが使用されることは比較的まれですが、赤黒ツリーは非常に広く使用されます。たとえば、Java の TreeMap は、赤黒ツリーを使用して、ソートされたキーと値のペアを格納します。Java 8 の HashMap は、リンクリストの赤黒ツリーを使用して、ハッシュの競合問題を解決します (競合するノードが少ない場合はリンク リストを使用し、競合するノードが少ない場合はリンク リストを使用します)。競合するノードが多い場合は、赤黒ツリーを使用します)。

データがメモリ内にある状況 (前述の TreeMap や HashMap など) では、赤黒ツリーのパフォーマンスは非常に優れています。ただし、

データがディスクなどの補助記憶装置 (

MySQL やその他のデータベースなど) にある状況では、赤黒ツリーは苦手です。なぜなら、赤黒の木はまだ高く成長しすぎているからです。データがディスク上にある場合、ディスク IO が最大のパフォーマンス ボトルネックになるため、設計目標は IO の数を最小限に抑えることです。ツリーの高さが高くなるほど、追加、削除、変更に必要な IO 時間は増加します。パフォーマンスに重大な影響を与える検索。 4. B ツリー: ディスクのために誕生

B

このツリーは B-# とも呼ばれます

##tree (- はマイナス記号ではありません) は、ディスクなどの補助記憶装置用に設計されたマルチパス分散検索ツリーです。バイナリ ツリーと比較すると、B ツリーの各非葉ノードは複数のサブツリーを持つことができます。 したがって、ノードの総数が同じである場合、B ツリーの高さは AVL ツリーおよび赤黒ツリーよりもはるかに小さく (B ツリーは「ダンプティ」です)、ディスク IO が大幅に削減されます。

B ツリーを定義する際の最も重要な概念は順序です。m 次の B ツリーの場合、次の条件を満たす必要があります:

• 各ノードには最大で m 個の子が含まれます。ノード。
• ルート ノードに子ノードが含まれる場合は、少なくとも 2 つの子ノードが含まれている必要があります。ルート ノードを除き、各非リーフ ノードには少なくとも m/2 の子ノードが含まれている必要があります。
• k 個の子ノードを持つ非リーフ ノードには、k - 1 個のレコードが含まれます。
• すべてのリーフ ノードは同じレイヤーにあります。

B ツリーの定義では、主に子ノードと非リーフ ノードのレコードの数が制限されていることがわかります。

次の図は 3 次 B ツリーの例です (画像ソース):

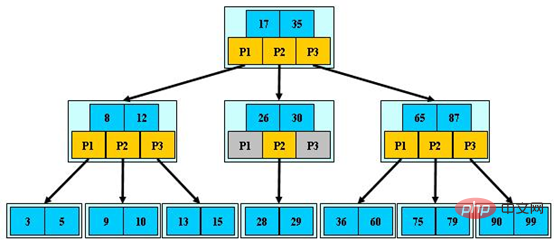
B ツリーの利点は次のとおりです。木の高さが低いだけでなく、局所的な領域にアクセスできる能力、性的原理の利用。いわゆる局所性原理とは、あるデータが使用されるとき、短時間のうちに近くのデータが使用される可能性が高いことを意味します。 B ツリーは、同じノードに同様のキーを持つデータを格納します。データの 1 つがアクセスされると、データベースはノード全体をキャッシュに読み取ります。隣接するデータがすぐにアクセスされると、キャッシュから直接読み取ることができます。ディスク IO が必要ないため、B ツリーのキャッシュ ヒット率が高くなります。

B ツリーはデータベースにいくつか応用されており、たとえば mongodb のインデックスは B ツリー構造を使用しています。ただし、多くのデータベース アプリケーションでは、B ツリーの変形である B ツリーが使用されます。

5. B ツリー

B ツリーもマルチパスバランス検索ツリーです。B ツリーとの主な違いは次のとおりです。 :

• B ツリーの各ノード (リーフ ノードと非リーフ ノードを含む) は実データを格納します。B ツリーのリーフ ノードのみが実データを格納し、非リーフ ノードは実データのみを格納しますキー。 MySQL では、ここで言及される実際のデータは、行のすべてのデータ (Innodb のクラスター化インデックスなど) である場合もあれば、行の主キー (Innodb の補助インデックスなど) のみの場合もあれば、行のアドレス ( MyIsam の非クラスター化インデックスなど)。
• B ツリー内のレコードは 1 回だけ出現し、繰り返し出現することはありませんが、B ツリーのキーは繰り返し出現する可能性があります。必ずリーフ ノードに出現するか、リーフ ノードに繰り返し出現する可能性があります。非リーフノード。
• B ツリーのリーフ ノードは、二重リンク リストを通じてリンクされています。
• B ツリー内の非リーフ ノードの場合、レコード数は子ノードの数より 1 減りますが、B ツリー内のレコード数は子ノードの数と同じです。 。

#したがって、B ツリーには、B ツリーと比較して次の利点があります。

• #IO 時間が少ない: The B ツリーの非リーフ ノードには実際のデータではなくキーのみが含まれるため、各ノードに格納されるレコードの数は B の数よりもはるかに多く (つまり、次数 m が大きくなります)、B の高さはツリーが低くなり、アクセス時間が短くなり、必要な IO 回数が少なくなります。さらに、各ノードがより多くのレコードを保存するため、アクセス局所性の原理がより有効に活用され、キャッシュ ヒット率が高くなります。
• 範囲クエリにより適しています: B ツリーで範囲クエリを実行する場合、最初に検出される下限を見つけてから、in-検索の上限が見つかるまで B ツリーの順序トラバースを実行し、B ツリーの範囲クエリはリンク リストをトラバースするだけで済みます。
• より安定したクエリ効率: B ツリーのクエリ時間の複雑さは 1 からツリーの高さ (それぞれルート ノードとリーフ ノードに対応) の間です。すべてのデータがリーフ ノードにあるため、B ツリーのクエリの複雑さはツリーの高さで安定しています。

B ツリーには欠点もあります。キーが繰り返されるため、より多くのスペースを必要とします。ただし、パフォーマンスの利点と比較すると、スペースの欠点は許容できる場合が多いため、データベースでは B ツリーよりも B ツリーの方が広く使用されています。

6. B-tree のパワーを実感してください

前述したように、赤黒ツリーなどの二分木と比較すると、B- Tree/B-tree が最も大きく、樹高が低いという利点があります。実際、Innodb の B インデックスの場合、ツリーの高さは通常 2 ～ 4 レベルです。以下に具体的な見積もりをしてみましょう。

ツリーの高さは次数によって決まります。次数が大きくなるほど、ツリーは短くなり、次数のサイズは各ノードが保存できるレコードの数によって決まります。 Innodb の各ノードはページ (ページ) を使用します。ページ サイズは 16KB で、そのうちメタデータは約 128 バイトのみを占め (ファイル管理ヘッダー情報、ページヘッダー情報などを含む)、スペースのほとんどはデータの保存に使用されます。 。

• 非リーフ ノードの場合、レコードにはインデックスのキーと次のレベルのノードへのポインタのみが含まれます。各非リーフ ページに 1000 レコードが格納されていると仮定すると、各レコードは約 16 バイトを占めます。インデックスが整数またはそれより短い文字列の場合、この仮定は妥当です。さらに言えば、インデックス列の長さをあまり大きくすべきではないという提案をよく聞きますが、その理由は次のとおりです: インデックス列が長すぎて各ノードに含まれるレコードが少なすぎると、ツリーが高くなりすぎてインデックス効果が低下します。大幅に削減され、インデックスにより多くのスペースが浪費されます。

• リーフ ノードの場合、レコードにはインデックスのキーと値が含まれます (値は行の主キー、データの完全な行などである可能性があります。詳細については前の記事を参照してください)。データ量が多くなります。ここでは、各リーフ ノード ページに 100 レコードが格納されていると仮定します (実際には、インデックスがクラスター化インデックスの場合、この数は 100 未満になる可能性があります。インデックスが補助インデックスの場合、この数は 100 よりはるかに大きくなる可能性があります。実際の状況に基づいて推定されます）。

3 層 B ツリーの場合、最初の層 (ルート ノード) には 1 ページがあり、1000 レコードを保存できます。2 番目の層には 1000 ページがあり、1000*1000 レコードを保存できます。 3 番目の層 (リーフ ノード) には 1000*1000 ページがあり、各ページには 100 レコードを保存できるため、1000*1000*100 レコード、つまり 1 億レコードを保存できます。バイナリ ツリーの場合、1 億レコードを保存するには約 26 層が必要です。

7. まとめ

最後に、さまざまなツリーによって解決された問題と直面した新たな問題をまとめます:

1) 、Binary Search Tree (BST): ソートの基本的な問題を解決しますが、バランスが保証できないため、リンク リストに退化する可能性があります;

2)、Balanced Binary Tree (AVL): の問題を解決します。回転によるバランスを取るが、回転演算効率が低すぎる;

3)、赤黒ツリー: 厳密なバランスを放棄し、赤黒ノードを導入することで、AVL 回転効率が低すぎる問題が解決されます。ただし、ディスクなどのシナリオでは、ツリーがまだ高すぎて IO 回数が多すぎます;

4)、B ツリー: バイナリ ツリーをマルチパスのバランスの取れた検索ツリーに変更することで、ツリーが高すぎる問題は解決されます;

5)、B ツリー: B ツリーに基づいて、非リーフ ノードがデータを格納しない純粋なインデックス ノードに変換され、ツリーの高さがさらに低くなります。さらに、リーフ ノードはポインターを使用してリンク リストに接続されるため、範囲クエリがより効率的になります。

推奨学習: MySQL チュートリアル

以上がMySQL がインデックス構造として B+ ツリーを選択するのはなぜですか? (詳しい説明)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。