C言語による最小スパニングツリーの実装-C#.Net チュートリアル-php.cn

C言語による最小スパニングツリーの実装

angryTom

リリース： 2019-11-29 15:24:04

転載

3641 人が閲覧しました

#1. 最小スパニングツリーの概要

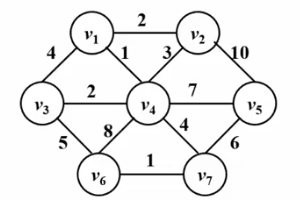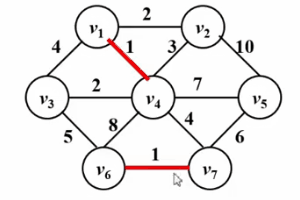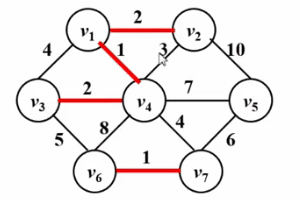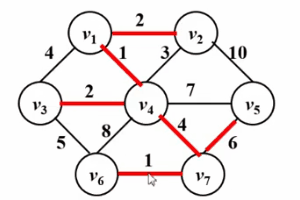
最小スパニングツリーとは何ですか?

最小スパニングツリー (最小スパニングツリー、MST) は、指定された無向グラフ G(V,E) 内でツリー T を見つけ、このツリーがグラフ G 内のすべての頂点と、すべての頂点をもつようにします。エッジはグラフ G のエッジからのものであり、ツリー全体のエッジの重みの最小合計を満たします。

2.prim アルゴリズム

は、ダイクストラのアルゴリズムに非常によく似ています。！次の Gif 図を見てください。プリムアルゴリズムの中心となるアイデアは、グラフ G (V, E) に集合 S を設定し、訪問した頂点を保存し、その頂点から最短距離が最小の頂点を選択することです。集合 S は、集合 V-S (u で示されます) から毎回アクセスし、集合 S に参加します。次に、頂点 u を中点とし、u から到達できるすべての頂点 v と集合 s との最短距離を最適化します。この操作は、セット s にすべての頂点が含まれるまで n 回実行されます。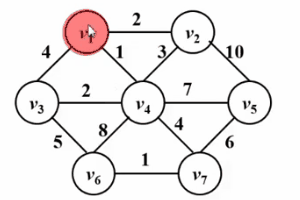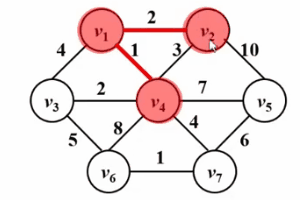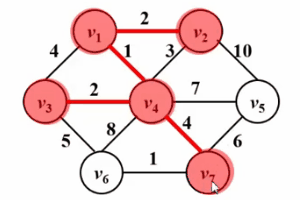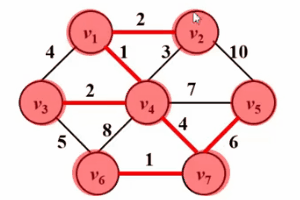

C言語による最小スパニングツリーの実装

違いは、ダイクストラのアルゴリズムの dist はソース点 s から頂点 w までの最短パスであるのに対し、プリムのアルゴリズムの dist は集合 S から頂点 w までの最短パスであることです。 , 以下は、それらの疑似コードの説明の比較です。ダイクストラアルゴリズムの詳細な説明については、記事

C言語による最小スパニングツリーの実装

アルゴリズムの実装:

#include<iostream>
#include<vector>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集 
int dist[MaxVertex]; // 距离 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
vector<Vertex> MST;  // 最小生成树 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图 
        dist[i] = INF;   // 初始化距离
        parent[i] = -1;  // 初始化并查集 
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        G[v1][v2] = w;
        G[v2][v1] = w;
    }
}
// Prim算法前的初始化 
void IniPrim(Vertex s){
    dist[s] = 0;
    MST.push_back(s);
    for(Vertex i =1;i<=Nv;i++)
        if(G[s][i]){
            dist[i] = G[s][i];
            parent[i] = s;
        } 
}
// 查找未收录中dist最小的点 
Vertex FindMin(){
    int min = INF;
    Vertex xb = -1;
    for(Vertex i=1;i<=Nv;i++)
        if(dist[i] && dist[i] < min){ 
            min = dist[i];
            xb = i;
        }
    return xb;
}
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<MST[i]<<" ";
    cout<<"权重和为："<<sum<<endl; 
    cout<<"该生成树为："<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
}
void Prim(Vertex s){
    IniPrim(s);
    while(1){
        Vertex v = FindMin();
        if(v == -1)
            break;
        sum += dist[v];
        dist[v] = 0;
        MST.push_back(v);
        for(Vertex w=1;w<=Nv;w++)
            if(G[v][w] && dist[w])
                if(G[v][w] < dist[w]){
                    dist[w] = G[v][w];
                    parent[w] = v;
                }
    }
}
int main(){
    build();
    Prim(1);
    output();
    return 0;
}

ログイン後にコピー

を参照してください。プリムアルゴリズムについてより詳しい説明については、ビデオ https://www.bilibili.com/video/av55114968?p=99

3.kruskal アルゴリズム ## を参照してください。 #Kruskal アルゴリズムも使用可能最小スパニングツリーの問題を解決するために、そのアルゴリズムのアイデアは理解しやすいです典型的なエッジグリーディ、そのアルゴリズムのアイデアは次のとおりです:

#● グラフ内のすべてのエッジを非表示にします初期状態。グラフ内の各頂点は 1 つの接続されたブロックであり、合計で n 個の接続されたブロックがあります。

#● すべてのエッジをエッジの重みに従って小さいものから大きいものまで並べ替えます。

● 小さいものから大きいものまでエッジの重みに従ってすべてのエッジをテストします。現在のテストエッジによって接続されている 2 つの頂点が同じ接続されたブロック内にない場合、テストエッジは現在の最小スパニングツリーに追加されます。それ以外の場合、エッジは追加されます。捨てられた。

# 最小スパニングツリー内のエッジの数が頂点の合計数から 1 を引いた値に等しくなるまで、またはすべてのエッジがテストされたときに終了するまで、前の手順を繰り返します。最後に終了した場合は、そのエッジの数がテストされます。最小スパニングツリーは頂点の総数から 1 を引いた値より小さく、グラフが接続されていないことを示します。

下のGIFをご覧ください。

アルゴリズムの実装:

#include<iostream>
#include<string>
#include<vector>
#include<queue>
#define INF 100000
#define MaxVertex 105
typedef int Vertex; 
int G[MaxVertex][MaxVertex];
int parent[MaxVertex];   // 并查集最小生成树 
int Nv;    // 结点 
int Ne;    // 边 
int sum;  // 权重和 
using namespace std; 
struct Node{
    Vertex v1;
    Vertex v2;
    int weight; // 权重 
    // 重载运算符成最大堆 
    bool operator < (const Node &a) const
    {
        return weight>a.weight;
    }
};
vector<Node> MST;  // 最小生成树 
priority_queue<Node> q;   // 最小堆 
// 初始化图信息 
void build(){
    Vertex v1,v2;
    int w;
    cin>>Nv>>Ne;
    for(int i=1;i<=Nv;i++){
        for(int j=1;j<=Nv;j++)
            G[i][j] = 0;  // 初始化图
        parent[i] = -1;
    }
    // 初始化点
    for(int i=0;i<Ne;i++){
        cin>>v1>>v2>>w;
        struct Node tmpE;
        tmpE.v1 = v1;
        tmpE.v2 = v2;
        tmpE.weight = w;
        q.push(tmpE); 
    }
}
//  路径压缩查找 
int Find(int x){
    if(parent[x] < 0)
        return x;
    else
        return parent[x] = Find(parent[x]);
} 
//  按秩归并 
void Union(int x1,int x2){
    if(parent[x1] < parent[x2]){
        parent[x1] += parent[x2];
        parent[x2] = x1;
    }else{
        parent[x2] += parent[x1];
        parent[x1] = x2;
    }
} 
void Kruskal(){
    // 最小生成树的边不到 Nv-1 条且还有边 
    while(MST.size()!= Nv-1 && !q.empty()){
        Node E = q.top();  // 从最小堆取出一条权重最小的边
        q.pop(); // 出队这条边 
        if(Find(E.v1) != Find(E.v2)){  // 检测两条边是否在同一集合 
            sum += E.weight; 
            Union(E.v1,E.v2);     // 并起来 
            MST.push_back(E);
        }
    }
    
} 
void output(){
    cout<<"被收录顺序："<<endl; 
    for(Vertex i=0;i<Nv;i++)
        cout<<MST[i].weight<<" ";
    cout<<"权重和为："<<sum<<endl; 
    for(Vertex i=1;i<=Nv;i++)
        cout<<parent[i]<<" ";
    cout<<endl;
}
int main(){
    build();
    Kruskal();
    output();
    return 0;
}

ログイン後にコピー