
Python の並べ替えアルゴリズムとは何ですか?次の記事では、Python の古典的な並べ替えアルゴリズムのトップ 10 を紹介します。一定の参考値があるので、困っている友達が参考になれば幸いです。

現在、多くのことがアルゴリズムで解決できるようになりました。プログラミングにおいて、アルゴリズムは非常に重要な役割を果たします。アルゴリズムを関数でカプセル化すると、プログラムがより良くなります。呼び出し、繰り返し書く必要はありません。 。
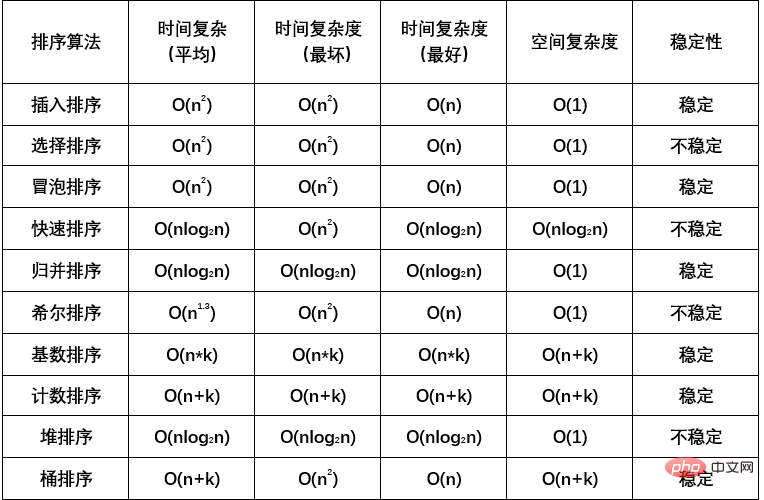
Python の古典的なアルゴリズム トップ 10:
1. 挿入ソート
1. アルゴリズムの考え方
2 番目の要素から開始して前の要素と比較し、前の要素が現在の要素より大きい場合は、次に、前の要素を後方に移動し、現在の要素を前方に移動し、それ以下の要素が見つかってその後ろに挿入します。
次に、3 番目の要素を選択し、上記の操作を繰り返し、挿入します。を選択し、順番に選択します。最後の要素を挿入すると、すべての並べ替えが完了します。
2. コードの実装
def insertion_sort(arr):
#插入排序
# 第一层for表示循环插入的遍数
for i in range(1, len(arr)):
# 设置当前需要插入的元素
current = arr[i]
# 与当前元素比较的比较元素
pre_index = i - 1
while pre_index >= 0 and arr[pre_index] > current:
# 当比较元素大于当前元素则把比较元素后移
arr[pre_index + 1] = arr[pre_index]
# 往前选择下一个比较元素
pre_index -= 1
# 当比较元素小于当前元素,则将当前元素插入在 其后面
arr[pre_index + 1] = current
return arr2. 選択の並べ替え
1.アルゴリズムの考え方
最初の要素を比較要素とし、次の要素と順番に比較し、すべての要素を比較して最小の要素を見つけ、それを最初の要素と交換し、上記の操作を繰り返します。 2 番目に小さい要素を見つけて 2 番目の位置の要素と交換し、以下同様に残りの最も小さい要素を見つけて前に移動します。つまり、並べ替えが完了します。
2. コードの実装
def selection_sort(arr):
#选择排序
# 第一层for表示循环选择的遍数
for i in range(len(arr) - 1):
# 将起始元素设为最小元素
min_index = i
# 第二层for表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
# 如果当前元素比最小元素小,则把当前元素角标记为最小元素角标
min_index = j
# 查找一遍后将最小元素与起始元素互换
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr3. バブル ソート
1 。アルゴリズムのアイデア
最初と 2 番目の比較を開始します。最初の値が 2 番目の値より大きい場合は、位置を交換し、2 番目と 3 番目の値を比較し、徐々に戻ります。最初のラウンドでは、最大の要素が最後にランク付けされています。
したがって、上記の操作を繰り返すと、2 番目に大きい要素が最後から 2 番目にランク付けされます。 、上記の操作を n-1 回繰り返して並べ替えを完了します。これは、前回の要素は 1 つだけであるため、比較は必要ありません。
2. コードの実装
def bubble_sort(arr):
#冒泡排序
# 第一层for表示循环的遍数
for i in range(len(arr) - 1):
# 第二层for表示具体比较哪两个元素
for j in range(len(arr) - 1 - i):
if arr[j] > arr[j + 1]:
# 如果前面的大于后面的,则交换这两个元素的位置
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr4. クイック ソート
1.アルゴリズム的思考
ベースライン条件を見つけ出します。ベースライン条件はできるだけ単純である必要があり、ベースライン条件が満たされるまで問題の分解 (またはサイズの縮小) を続けます。
2. コードの実装
def quick_sort(arr):
if len(arr) < 2:
# 基线条件:为空或只包含一个元素的数组是“有序”的
return arr
else:
# 递归条件
pivot = arr[0]
# 由所有小于基准值的元素组成的子数组
less = [i for i in arr[1:] if i <= pivot]
# 由所有大于基准值的元素组成的子数组
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quick_sort([10, 5, 2, 3]))5. マージ ソート
1.アルゴリズムの考え方
マージ ソートは分割統治法の典型的な応用例です。分割統治法 (pide-and-Conquer): 元の問題を、元の問題と同様の構造を持つ n 個の小さなサブ問題に分割し、これらの問題を再帰的に解決し、その結果を組み合わせて元の問題の解を取得します。分解されたシーケンスは二分木のように見えます。
具体的な実装手順:
二分法を使用して再帰を使用してソース シーケンスを複数のサブシーケンスに分割します
2 つのサブ列を分割するためのスペースを申請します。 サブ列を並べ替えてマージしてから返します。
すべてのサブ列を段階的にマージし、最終的に並べ替えを完了します。
#2. コードの実装#def merge_sort(arr):
#归并排序
if len(arr) == 1:
return arr
# 使用二分法将数列分两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
#排序合并两个数列
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result
##1. アルゴリズムのアイデア
ヒル ソートの全体的なアイデアは、複数の要素を一定の間隔で並べ替えてから、間隔を減らすことです。このようにして、最終シーケンスは基本的な順序シーケンスになります。 具体的な手順:
増分 (間隔) 値の計算
要素と増分要素を比較します。たとえば、次のような場合です。増分値が 7 の場合、0、7、14、21... 要素の並べ替え
を挿入し、次に 1、8、15... 要素を昇順で並べ替えます。
すべての要素が並べ替えられたら、増分をたとえば 3 に減らし、上記の手順 2 と 3 を繰り返します。
最後に減らします。 1 ずつ増分すると、シーケンスは基本的に順序通りになり、最後の通常の挿入を行うことができます
def shell_sort(arr):
#希尔排序
# 取整计算增量(间隔)值
gap = len(arr) // 2
while gap > 0:
# 从增量值开始遍历比较
for i in range(gap, len(arr)):
j = i
current = arr[i]
# 元素与他同列的前面的每个元素比较,如果比前面的小则互换
while j - gap >= 0 and current < arr[j - gap]:
arr[j] = arr[j - gap]
j -= gap
arr[j] = current
# 缩小增量(间隔)值
gap //= 2
return arr7. 基数ソート
1. アルゴリズムの考え方
基数ソート(radix sort)は「分布ソート」に属し、 「バケット ソート」またはビン ソートとも呼ばれ、その名前が示すように、ソート効果を達成するためにキー値情報の一部を通じてソート対象の要素を特定の「バケット」に割り当てます。基数ソート方式は安定したソートです。時間計算量は O (nlog(r)m) です。ここで、r は取得される基数、m はヒープの数です。場合によっては、基数ソート方法が他の安定した方法よりも効率的である場合があります。性的ランキング方法。
2. コード実装2.1 はバケット ソートから変換され、最下位ビットから最上位ビットへのバケット ソートが行われ、最終的に最終的なランク付けされたリストが出力されます。 def RadixSort(list,d):
for k in range(d):#d轮排序
# 每一轮生成10个列表
s=[[] for i in range(10)]#因为每一位数字都是0~9,故建立10个桶
for i in list:
# 按第k位放入到桶中
s[i//(10**k)%10].append(i)
# 按当前桶的顺序重排列表
list=[j for i in s for j in i]
return list
from random import randint
def radix_sort():
A = [randint(1, 99999999) for _ in xrange(9999)]
for k in xrange(8):
S = [ [] for _ in xrange(10)]
for j in A:
S[j / (10 ** k) % 10].append(j)
A = [a for b in S for a in b]
for i in A:
print i八、计数排序
1.算法思想
对每一个输入元素x,确定小于x的元素个数。利用这一信息,就可以直接把x 放在它在输出数组上的位置上了,运行时间为O(n),但其需要的空间不一定,空间浪费大。
2.代码实现
from numpy.random import randint
def Conuting_Sort(A):
k = max(A) # A的最大值,用于确定C的长度
C = [0]*(k+1) # 通过下表索引,临时存放A的数据
B = (len(A))*[0] # 存放A排序完成后的数组
for i in range(0, len(A)):
C[A[i]] += 1 # 记录A有哪些数字,值为A[i]的共有几个
for i in range(1, k+1):
C[i] += C[i-1] # A中小于i的数字个数为C[i]
for i in range(len(A)-1, -1, -1):
B[C[A[i]]-1] = A[i] # C[A[i]]的值即为A[i]的值在A中的次序
C[A[i]] -= 1 # 每插入一个A[i],则C[A[i]]减一
return B九、堆排序
1.算法思想
堆分为最大堆和最小堆,是完全二叉树。堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现 ,
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。
2.代码实现
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)十、桶排序
1.算法思想
为了节省空间和时间,我们需要指定要排序的数据中最小以及最大的数字的值,来方便桶排序算法的运算。
2.代码实现
#桶排序
def bucket_sort(the_list):
#设置全为0的数组
all_list = [0 for i in range(100)]
last_list = []
for v in the_list:
all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
for i,t_v in enumerate(all_list):
if t_v != 0:
for j in range(t_v):
last_list.append(i)
return last_list总结:
在编程中,算法都是相通的,算法重在算法思想,相当于将一道数学上的应用题的每个条件,区间,可能出现的结果进行分解,分步骤的实现它。算法就是将具体问题的共性抽象出来,将步骤用编程语言来实现。通过这次对排序算法的整理,加深了对各算法的了解,具体的代码是无法记忆的,通过对算法思想的理解,根据伪代码来实现具体算法的编程,才是真正了解算法。
推荐学习:Python视频教程
以上がPythonのソートアルゴリズムとは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。