
#再帰とは何ですか?
#プログラムが自分自身を呼び出すプログラミング手法は再帰と呼ばれます。
アルゴリズムとしての再帰は、プログラミング言語で広く使用されています。プロセスまたは関数には、その定義または説明でそれ自体を直接または間接的に呼び出すメソッドがあります。通常、大規模で複雑な問題を、元の問題と同様の小さな問題に変換して解決します。再帰的戦略のみが必要です。必要なプログラムの数は少ないです。問題解決プロセスで必要となる複数の繰り返し計算を記述するため、プログラム コードの量が大幅に削減されます。再帰の力は、有限のステートメントを使用してオブジェクトの無限のコレクションを定義することにあります。
一般に、再帰には境界条件、再帰的な前方セクションと再帰的な戻りセクションが必要です。境界条件が満たされない場合、再帰は続行され、境界条件が満たされる場合、再帰は戻ります。
入れ子関数呼び出しプロセスの例
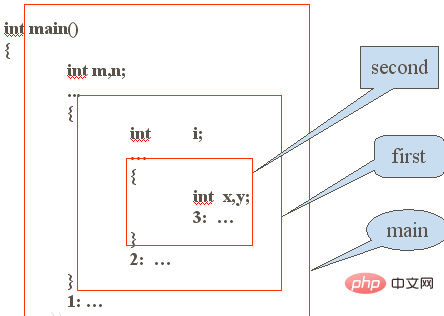
再帰を構成するために必要な条件:
1 。サブ問題は元の問題と同じであり、より単純である必要があります;
2. 無制限にそれ自体を呼び出すことはできず、出口が存在する必要があり、非単純化することもできます。 -再帰的状況処理。
数学とコンピューター サイエンスでは、再帰とは、1 つ (または複数) の単純な基本ケースによって定義されるオブジェクトまたはメソッドのクラスを指し、他のすべてのケースを基本ケースの条件に帰着できることを規定します。
数学とコンピューター サイエンスでは、再帰とは、1 つ (または複数) の単純な基本ケースによって定義されるオブジェクトまたはメソッドのクラスを指しますが、他のすべてのケースはその基本ケースに帰着できるという条件が付けられています。
たとえば、次は誰かの祖先の再帰的定義です: 誰かの両親はその人の祖先です (基本ケース)。
誰かの祖先の親は、誰かの祖先でもあります (再帰ステップ)。黄金分割数列としても知られるフィボナッチ数列は、1、1、2、3、5、8、13、21.... I [1]
フィボナッチ数列は次のような数列を指します。再帰の典型的なケース: 再帰的関係とは、エンティティがそれ自体との関係を確立することです。
Fib(0) = 1 [基本ケース] Fib(1) = 1 [基本ケース] すべての整数 n > 1 の場合: Fib(n) = (Fib(n-1) Fib(n -2) )) [再帰的定義] 多くの数学関数は再帰的に表現できますが、実際のアプリケーションでは、再帰的定義のオーバーヘッドが高く、法外なことがよくあります。例:
Factorial (1) = 1 [基本的なケース] すべての整数 n > 1: Factorial (n) = (n * Factorial (n-1)) [再帰的定義] 理解しやすいメンタル モデルでは、再帰的定義は、同じタイプの「以前に定義された」オブジェクトの観点からオブジェクトを定義します。例: 100 個の箱をどうやって移動できますか?答え: まずボックスを移動し、どこに移動したかを記録してから、より小さな問題に移ります。99 個のボックスをどうやって移動できるでしょうか?最終的に、問題は箱を移動する方法になりますが、あなたはすでにその方法を知っています。
このような定義は数学では非常に一般的です。たとえば、集合論における自然数の正式な定義は次のとおりです。1 は自然数であり、すべての自然数には後続の数があり、それも自然数です。
ドロステ効果
ドロステ効果は、再帰の視覚的な形式です。女性が持っている物の中には、同じ物を持っている自分の小さな写真があり、さらに同じ物を持っているさらに小さい写真もあり、というように続きます。
別の例として、燃えているろうそくを 2 つの向かい合った鏡の間に置くと、一方の鏡にはろうそくが見え、ろうそくの後ろには鏡があり、鏡の中には別のろうそくがあります。キャンドル...これも再帰の現れです。
関連知識の詳細については、PHP 中国語 Web サイト をご覧ください。 !
以上が再帰とは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。