Python で数式を使用して π を計算する方法

Python は数式を使用して π を計算します。まず数学モジュールと時間モジュールをインポートし、次に円周率を小数点以下の数桁まで計算します。コードは [print('\n{:=^70}') .format ('計算開始'))]; 最後に計算が完了し、コードは [print('\n{:=^70}'] です。

#[関連研究の推奨事項:

python チュートリアル

]

Python の数式を使用して π を計算する方法:

1. はじめにから π

πの紹介

円周率はギリシャ文字の π (pài と発音) で表され、定数 (約 3.141592654 に等しい) であり、円周率を表します。円周率と円の直径は無限大です日常生活では、通常、近似計算の円周率を表すために 3.14 が使用されます。 1965 年、英国の数学者ジョン ウォー ジョン ウォリスは、数式を導き出し、円周率が無限の分数を掛け合わせた積に等しいことを発見した数学モノグラフを出版しました。ロチェスター大学の教授 科学者たちは、水素原子のエネルギー準位の量子力学的計算で円周率と同じ式を発見しました。小数点以下 31.4 兆桁

ここでは、私が解くのに「良い」と感じた式を使用します。計算結果は比較的正確なので良いのですが、計算には時間がかかります。一緒にやってみましょう。勉強しましょう~~~

2. π
• ##の近似計算

  # 1. 計算式

2. 方法の説明

# 式や方程式の右辺の分子使用するすべて 1 で、分母は増加数列です。最初の項から始めて、奇数項の符号は正、偶数項の符号は負です。方程式の右辺の分母が大きいほど、小さくなります。円周率の計算値はより正確になります。言い換えると、方程式の右側の項が多いほど、計算値の精度が高くなります。

3. コードの実装 (Python)

##

 1 from math import fabs           #导入数学模块
 2 from time import perf_counter   #导入时间模块
 3 
 4 def Bar(i):         #动态文本条
 5     N = pow(10,level)
 6     a = int((i/N)*50)
 7     b = 50 - a
 8     Y , N = '*' * a , '.' * b
 9     print("\r计算中：{:3.0f}% [{}->{}] {:.2f}s"
10           .format(2*a,Y,N,perf_counter()),end='')
11     
12 level = eval(input('计算Pi精确到小数点后几位数：'))
13 print('\n{:=^70}'.format('计算开始'))
14 a,b,pi,tmp = 1,1,0,1
15 i = 0
16 '''
17 a 分子  |  b 分母  |  pi 圆周率
18 tmp 存储a/b的值    |  i  执行进度
19 '''
20 perf_counter()      #开始计时
21 while (fabs(tmp) >= pow(10,-level)): #计算Pi
22     pi += tmp
23     b += 2
24     a = -a
25     tmp = a/b
26     i += 2
27     Bar(i)          #调用函数，实时显示计算进度
28 
29 print('\n{:=^70}'.format('计算完成'))
30 print('\nPi的计算值为：{}'.format(round(pi*4,level))) #输出计算结果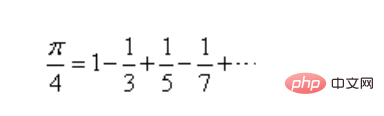

4. 画像の例

# 上の 3 つの写真からわかるように、小数点以下 4 桁まで正確に測定するには 14.07 秒しかかかりません。また、小数点以下 6 桁まで正確に測定するには 6 秒かかります。小数点以下の桁数は 124.61 秒で、小数点以下 8 桁までの精度には 850 / 8% = 10625 秒が必要で、これは約 177 分、つまり 2.95 時間です。この方法は優れていますが、それでも計算に時間がかかります。

以上がPython で数式を使用して π を計算する方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。