JavaScript のクイックソートの詳細な分析

はじめに

並べ替えとは、線形リストの要素を特定の順序 (数値またはアルファベット順) で配置することを指します。並べ替えは、多くの場合、検索と組み合わせて使用​​されます。

並べ替えアルゴリズムは数多くありますが、これまでで最も高速なものの 1 つは Quicksort(Quicksort) です。

クイックソートは、分割統治戦略を使用して、指定されたリスト要素を並べ替えます。これは、サブ問題が直接解決できるほど単純になるまで、アルゴリズムが問題をサブ問題に分割することを意味します。

アルゴリズム的には、これは再帰またはループを使用して実現できます。しかし、この問題では再帰を使用する方が自然です。

クイック ソートの背後にあるロジックを理解する

最初にクイック ソートの仕組みを見てみましょう:

1. 配列内の要素を選択します。この要素は Benchmark と呼ばれます（ピボット）＃＃＃。通常、配列内の最初または最後の要素が基礎として使用されます。
次に、ピボットの左側のすべての要素がピボットより小さく、右側のすべての要素がピボットより大きくなるように、配列の要素を再配置します。このステップは
2. パーティショニング と呼ばれます。要素がベースと等しい場合、それがどちら側にあるかは関係ありません。
配列がソートされるまで、ベンチマークの左側と右側でこのプロセスを繰り返します。

次に、例を通してこれらの手順を理解します。ソートされていない要素

[7, -2, 4, 1, 6, 5, 0, -4, 2] を含む配列があるとします。最後の要素をベースとして選択します。配列の分解ステップを以下の図に示します。

アルゴリズムのステップ 1 でベースとして選択された要素が色付けされます。分割後、基本要素は常に配列内の正しい位置にあります。

太字の黒い境界線が付いた配列は、その特定の再帰的分岐の最後でどのようになるかを表しており、結果として得られる配列には 1 つの要素のみが含まれます。

最後に、アルゴリズムの結果の並べ替えを確認できます。

JavaScript を使用してクイック ソートを実装する

このアルゴリズムのバックボーンは「パーティショニング」ステップです。再帰を使用するかループを使用するかに関係なく、この手順は同じです。

配列分割のコードが最初に記述されるのはまさにこの機能のためです。

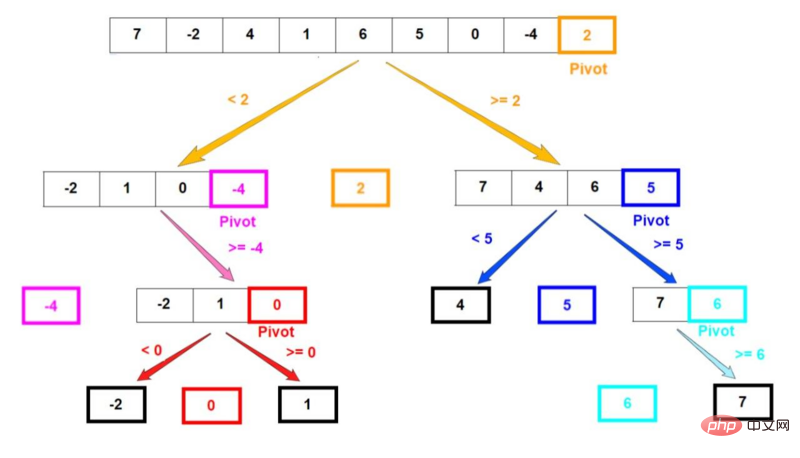
partition():

function partition(arr, start, end){
    // 以最后一个元素为基准
    const pivotValue = arr[end];
    let pivotIndex = start; 
    for (let i = start; i < end; i++) {
        if (arr[i] < pivotValue) {
        // 交换元素
        [arr[i], arr[pivotIndex]] = [arr[pivotIndex], arr[i]];
        // 移动到下一个元素
        pivotIndex++;
        }
    }
    
    // 把基准值放在中间
    [arr[pivotIndex], arr[end]] = [arr[end], arr[pivotIndex]] 
    return pivotIndex;
};

コードは最後の要素に基づいており、変数

pivotIndex を使用して、左側のすべての要素が pivotValue より小さく、右側の要素が pivotValue より大きい「中間」位置を追跡します。

最後のステップでは、ピボット (最後の要素) を

pivotIndex と交換します。

再帰的実装

partition() 関数を実装した後、問題を再帰的に解決し、パーティショニング ロジックを適用して残りの手順を完了する必要があります。 #この関数では、まず配列が分割され、次に左右の部分配列が分割されます。この関数が空でない配列、または複数の要素を含む配列を受け取る限り、このプロセスは繰り返されます。

空の配列と 1 つの要素のみを含む配列は、並べ替えられているとみなされます。

最後に、次の例を使用してテストします。

function quickSortRecursive(arr, start, end) {
    // 终止条件
    if (start >= end) {
        return;
    }
    
    // 返回 pivotIndex
    let index = partition(arr, start, end);
    
    // 将相同的逻辑递归地用于左右子数组
    quickSort(arr, start, index - 1);
    quickSort(arr, index + 1, end);
}

出力:

array = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortRecursive(array, 0, array.length - 1)

console.log(array)

ループ実装

クイック ソートの再帰的方法は、より直感的です。ただし、ループを使用してクイック ソートを実装することは、面接で比較的よくある質問です。

ほとんどの再帰的からループへの変換ソリューションと同様に、最初に思い浮かぶのは、スタックを使用して再帰的呼び出しをシミュレートすることです。これにより、使い慣れた再帰ロジックを再利用してループ内で使用できるようになります。

残りの未ソートの部分配列を追跡する方法が必要です。 1 つのアプローチは、特定のソートされていない部分配列の

start

と

end を表す要素の「ペア」をスタック上に単純に保持することです。 JavaScript には明示的なスタック データ構造がありませんが、配列は push()

関数と

pop() 関数をサポートします。ただし、peek() 関数はサポートされていないため、stack [stack.length-1] を使用してスタックの先頭を手動で確認する必要があります。 再帰的方法と同じ「分割」機能を使用します。クイックソート部分の書き方を見てみましょう:

-4,-2,0,1,2,4,5,6,7

テスト コードは次のとおりです:

function quickSortIterative(arr) {
    // 用push()和pop()函数创建一个将作为栈使用的数组
    stack = [];
    
    // 将整个初始数组做为“未排序的子数组”
    stack.push(0);
    stack.push(arr.length - 1);
    
    // 没有显式的peek()函数
    // 只要存在未排序的子数组，就重复循环
    while(stack[stack.length - 1] >= 0){
        
        // 提取顶部未排序的子数组
        end = stack.pop();
        start = stack.pop();
        
        pivotIndex = partition(arr, start, end);
        
        // 如果基准的左侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex - 1 > start){
            stack.push(start);
            stack.push(pivotIndex - 1);
        }
        
        // 如果基准的右侧有未排序的元素，
        // 则将该子数组添加到栈中，以便稍后对其进行排序
        if (pivotIndex + 1 < end){
            stack.push(pivotIndex + 1);
            stack.push(end);
        }
    }
}

出力:

ourArray = [7, -2, 4, 1, 6, 5, 0, -4, 2]
quickSortIterative(ourArray)

console.log(ourArray)

ビジュアル デモンストレーション

並べ替えアルゴリズムについて言えば、それらを視覚化すると、アルゴリズムがどのように機能するかを直感的に理解するのに役立ちます。次の例は Wikipedia からの引用です:

図の最後の要素は、基準。分割された配列を指定して、完全にソートされるまで左側を再帰的に走査します。次に右側を並べ替えます。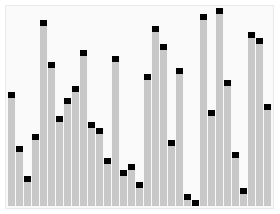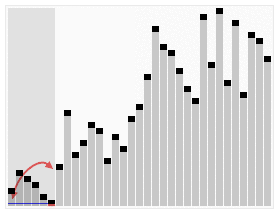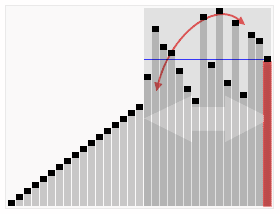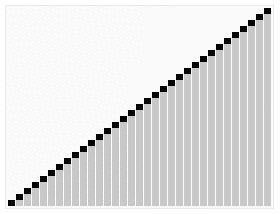

クイックソートの効率

次に、その時間と空間の複雑さについて説明します。クイック ソートの最悪の場合の時間計算量は $O(n^2)$ です。平均時間計算量は $O(n\log n)$ です。通常、最悪のシナリオは、ランダム化されたバージョンのクイックソートを使用することで回避できます。

クイックソート アルゴリズムの弱点は、ベンチマークの選択です。間違ったピボット (ほとんどの要素よりも大きいまたは小さいピボット) を選択するたびに、時間計算量は最悪の状態になります。基底を繰り返し選択するときに、要素の値が要素の基底より小さいか大きい場合、時間計算量は $O(n\log n)$ になります。

どのデータ ベンチマーク選択戦略が採用されても、クイック ソートの時間計算量は $O(n\log n)$ になる傾向があることが経験から観察できます。

クイックソートは追加のスペースを必要としません (再帰呼び出し用に予約されたスペースを除く)。このアルゴリズムは in-place アルゴリズムと呼ばれ、余分なスペースは必要ありません。

プログラミング関連の知識について詳しくは、プログラミング入門をご覧ください。 ！

以上がJavaScript のクイックソートの詳細な分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。