バブルソート、クイックソート、ヒープソートの時間計算量はどれくらいですか?

バブルソートの時間計算量: 最良の場合は「O(n)」、最悪の場合は「O(n2)」です。クイック ソートの時間計算量: 最良の場合は「O(nlogn)」、最悪の場合は「O(n2)」です。ヒープソートの時間計算量は「O(nlogn)」です。

このチュートリアルの動作環境: Windows 7 システム、Dell G3 コンピューター。

バブルソート

時間計算量

最良のケース: 配列自体はシーケンシャルであり、外側のループの走査は 1 回で完了しますO(n)

最悪のシナリオ: 配列自体が逆の順序であり、内側と外側のループが O(n2)

## を通過します。

#空間の複雑さ 空間交換シーケンスを作成します
O(1)
安定性
安定性。判断が確立されない場合、順序は交換されず、同じ要素も交換されません。

# バブル ソートは、すべてのソート アルゴリズムの中で最も単純です。ただし、実行時間の観点から見ると、バブル ソートは最も悪いものであり、その
• 複雑さは O(n2)

  です。

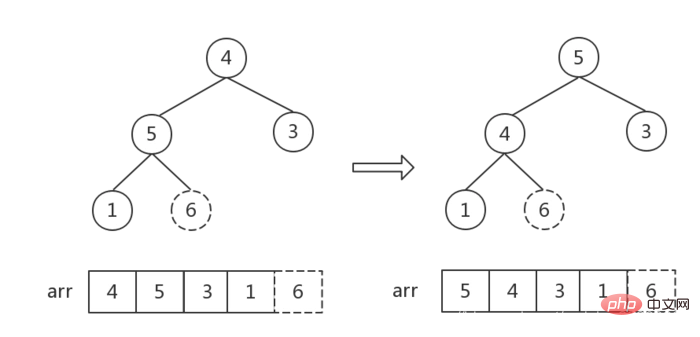
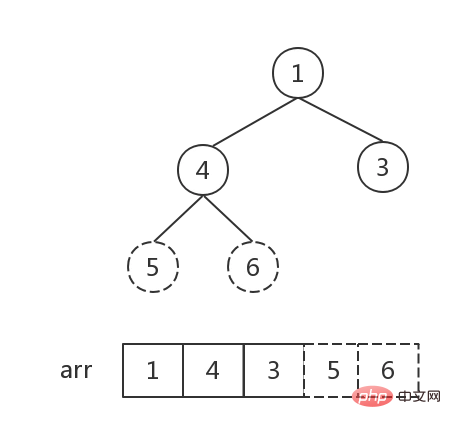
バブル ソートは、隣接する 2 つの項目を比較し、最初の項目が 2 番目の項目より大きい場合にそれらを交換します。まるで
• バブルが表面に上昇しているかのように、要素が正しい順序に移動されます

  。そのため、バブル ソートという名前が付けられています。

交換する場合、特定の交換アイテムの値を保存するために中間値を使用します。他の並べ替えメソッドもこのメソッドを使用するため、再利用のためにこの交換コードを配置するメソッドを宣言します。 ES6 (ECMAScript 2015) ** 拡張オブジェクト プロパティ - オブジェクト配列の代入構文の構造化を使用すると、** この関数は次のように記述できます:

• [array[index1], array[index2]] = [array[index2], array[index1]];

具体的な実装:

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {//外循环（行{2}）会从数组的第一位迭代 至最后一位，它控制了在数组中经过多少轮排序
    for (let j = 0; j < arr.length - i; j++) {//内循环将从第一位迭代至length - i位，因为后i位已经是排好序的，不用重新迭代
      if (arr[j] > arr[j + 1]) {//如果前一位大于后一位
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];//交换位置
      }
    }
  }
  return arr;
}

クイックソート

時間計算量

最良のシナリオ: 各基本値が配列全体を均等に分割します。 #O(nlogn)
最悪のシナリオ: 各基本値は、配列内の最大/最小値です。 O(n2)

空間複雑度

クイック ソート 再帰的であり、次の使用が必要です。再帰の各レベルの呼び出し情報を保存するためのスタックの数。そのため、空間の複雑さは再帰ツリーの深さと一致します。 最良のシナリオ: 各基本値は配列全体を均等に分割するだけで、再帰ツリーの深さは同じになります。
O(logn)
最悪の場合: すべての基本値は配列内の最大/最小値、つまり再帰ツリーの深さですO(n)
##安定性

クイックソートは、同じキーワードが交換される可能性があるため、不安定です。 クイック ソートは再帰的です。
特別な場合: left>right、直接終了します。
ステップ:

(1) まず、配列から中央の項目を pivotbase (通常は

最初の値) として選択します。

。 (2) 2 つのポインターを作成します。左側のポインターは配列の最初の項目を指し、右側のポインターは配列の最後の項目を指します。

ピボット

より小さい要素が見つかるまで右ポインタを移動し、ピボット より大きい要素が見つかるまで 左ポインタを移動してから それらを交換します 、左ポインタが右ポインタに出会うまでこのプロセスを繰り返します。このプロセスにより、ピボットより小さい値はピボットの前に並べ替えられ、ピボットより大きい値はピボットの後に並べ替えられます。このステップを 除算操作 と呼びます。 (3) 次に、 ピボット要素と、ポインターが停止した位置の要素 を交換します (これは、要素

を元の位置

に戻すのと同じです。この要素の左側の要素は要素 Small よりも小さく、右側の要素は彼よりも大きく、この位置が彼の最終位置です) (4) 次に、アルゴリズムは、小さな配列 (ピボット要素よりも小さい値で構成されるサブ配列、およびピボット要素よりも小さい値で構成されるサブ配列)、Yuanda 値で構成されるサブ配列) 前の 2 つの手順を繰り返します (再帰的メソッド

) )、

再帰的終了は left/right=i

、つまり

left>i-1 / i+1>right

この時点で、部分配列配列はソートされています。

ホーミング図:

具体的な実装: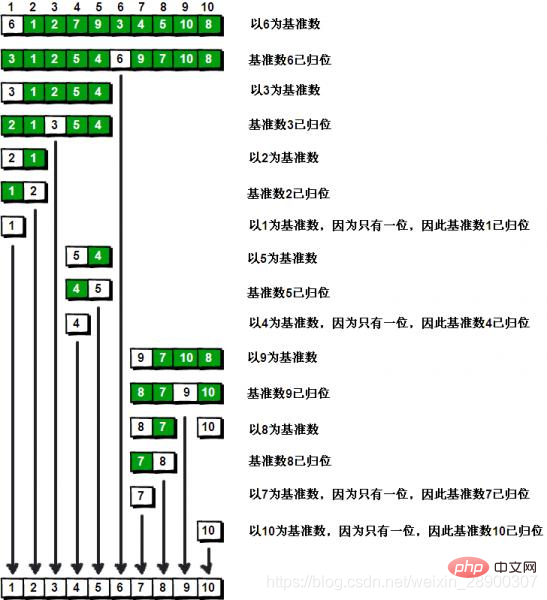

function quicksort(arr, left, right) {
  if (left > right) {
    return;
  }
  var i = left,
    j = right,
    base = arr[left]; //基准总是取序列开头的元素
  //   var [base, i, j] = [arr[left], left, right]; //以left指针元素为base
  while (i != j) {
    //i=j，两个指针相遇时，一次排序完成，跳出循环
    // 因为每次大循环里面的操作都会改变i和j的值，所以每次循环/操作前都要判断是否满足i<j
    while (i < j && arr[j] >= base) {
      //寻找小于base的右指针元素a，跳出循环，否则左移一位
      j--;
    }
    while (i < j && arr[i] <= base) {
      //寻找大于base的左指针元素b，跳出循环，否则右移一位
      i++;
    }
    if (i < j) {
      [arr[i], arr[j]] = [arr[j], arr[i]]; //交换a和b
    }
  }
  [arr[left], arr[j]] = [arr[j], arr[left]]; //交换相遇位置元素和base，base归位
  //   let k = i;
  quicksort(arr, left, i - 1); //对base左边的元素递归排序
  quicksort(arr, i + 1, right); //对base右边的元素递归排序
  return arr;
}

参考: https://www.cnblogs.com/venoral/p/5180439.html

ヒープソート

ヒープの概念

• 堆是一个完全二叉树。
• 完全二叉树： 二叉树除开最后一层，其他层结点数都达到最大，最后一层的所有结点都集中在左边（左边结点排列满的情况下，右边才能缺失结点）。
• 大顶堆：根结点为最大值，每个结点的值大于或等于其孩子结点的值。
• 小顶堆：根结点为最小值，每个结点的值小于或等于其孩子结点的值。
• 堆的存储： 堆由数组来实现，相当于对二叉树做层序遍历。如下图：
  
  

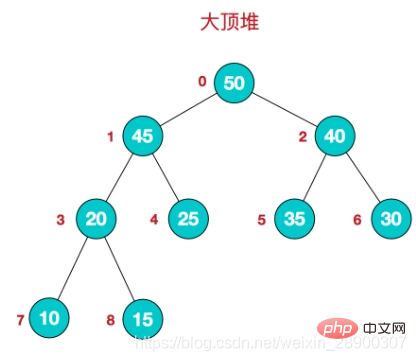
时间复杂度
总时间为建堆时间+n次调整堆 —— O(n)+O(nlogn)=O(nlogn)
建堆时间：从最后一个非叶子节点遍历到根节点，复杂度为O(n)
n次调整堆：每一次调整堆最长的路径是从树的根节点到叶子结点，也就是树的高度logn，所以每一次调整时间复杂度是O(logn)，一共是O(nlogn)

空间复杂度
堆排序只需要在交换元素的时候申请一个空间暂存元素，其他操作都是在原数组操作，空间复杂度为O(1)

稳定性
堆排序是不稳定的，因为可能会交换相同的子结点。

步骤一：建堆

• 以升序遍历为例子，需要先将将初始二叉树转换成大顶堆，要求满足：树中任一非叶子结点大于其左右孩子。
• 实质上是调整数组元素的位置，不断比较，做交换操作。
• 找到第一个非叶子结点——Math.floor(arr.length / 2 - 1)，从后往前依次遍历
• 对每一个结点，检查结点和子结点的大小关系，调整成大根堆

// 建立大顶堆
function buildHeap(arr) {
  //从最后一个非叶子节点开始，向前遍历，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则
  }
}

步骤二：调整指定结点形成大根堆

• 建立childMax指针指向child最大值节点，初始值为2 * cur + 1，指向左节点
• 当左节点存在时（左节点索引小于数组length），进入循环，递归调整所有节点位置，直到没有左节点为止（cur指向一个叶结点为止），跳出循环，遍历结束
• 每次循环，先判断右节点存在时，右节点是否大于左节点，是则改变childMax的指向
• 然后判断cur根节点是否大于childMax，
• 大于的话，说明满足大顶堆规律，不需要再调整，跳出循环，结束遍历
• 小于的话，说明不满足大顶堆规律，交换根节点和子结点，
• 因为交换了节点位置，子结点可能会不满足大顶堆顺序，所以还要判断子结点然后，改变cur和childMax指向子结点，继续循环判断。

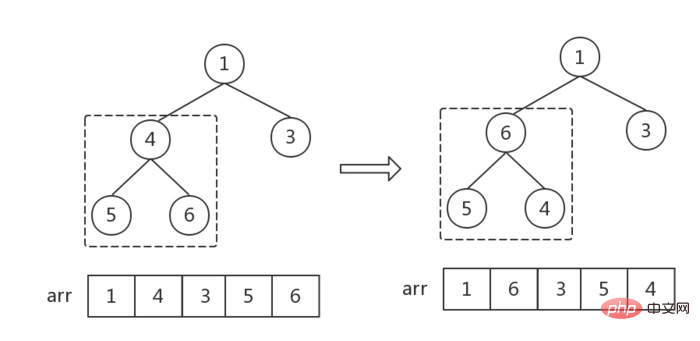
//从输入节点处调整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引

  //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构
  while (childMax < len) {
    //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子树值小于根节点，不需要调整，退出循环
    if (arr[childMax] < arr[cur]) break;
    //子树值大于根节点，需要调整，先交换根节点和子节点
    swap(arr, childMax, cur);
    cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则
    childMax = 2 * cur + 1; //子节点指针指向新的子节点
  }
}

步骤三：利用堆进行排序

• 从后往前遍历大顶堆（数组），交换堆顶元素a[0]和当前元素a[i]的位置，将最大值依次放入数组末尾。
• 每交换一次，就要重新调整一下堆，从根节点开始，调整根节点～i-1个节点（数组长度为i），重新生成大顶堆
  
  

// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //构建大顶堆
  buildHeap(arr);
  //从后往前遍历，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置
    headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆
  }
  return arr;
}

完整代码：

// 交换数组元素
function swap(a, i, j) {
  [a[i], a[j]] = [a[j], a[i]];
}
//从输入节点处调整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引

  //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构
  while (childMax < len) {
    //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子树值小于根节点，不需要调整，退出循环
    if (arr[childMax] < arr[cur]) break;
    //子树值大于根节点，需要调整，先交换根节点和子节点
    swap(arr, childMax, cur);
    cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则
    childMax = 2 * cur + 1; //子节点指针指向新的子节点
  }
}
// 建立大顶堆
function buildHeap(arr) {
  //从最后一个非叶子节点开始，向前遍历，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则
  }
}
// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //构建大顶堆
  buildHeap(arr);
  //从后往前遍历，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置
    headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆
  }
  return arr;
}

更多编程相关知识，请访问：编程视频！！

以上がバブルソート、クイックソート、ヒープソートの時間計算量はどれくらいですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。