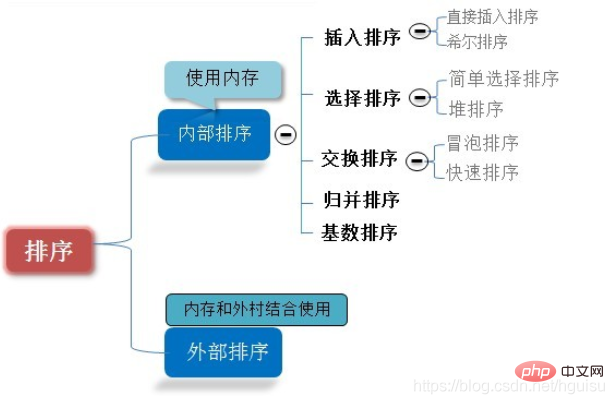
8 つの主要なソート アルゴリズムは次のとおりです: 1. 直接挿入ソート、2. ヒル ソート、3. 単純選択ソート、4. ヒープ ソート、5. バブル ソート、6. クイック ソート、7. マージ ソート、7. マージ ソート。 8. バケットソート/基数ソート。
このチュートリアルの動作環境: Windows 10 システム、Dell G3 コンピューター。
並べ替えには、内部並べ替えと外部並べ替えがあります。内部並べ替えはメモリ内のデータ レコードを並べ替えることですが、外部並べ替えは、並べ替えられたデータが非常に大きく、並べ替えられたすべてのレコードを一度に収容できないためです。ソートプロセス 外部ストレージ。
ここで説明する 8 つの主要な並べ替えは内部並べ替えです。
n が大きい場合、時間計算量が O(nlog2n) のソート方法 (クイック ソート、ヒープ ソート、またはマージ ソート) を使用する必要があります。
クイックソート: 比較に基づく内部ソートの中で現在最も優れた方法と考えられています。ソート対象のキーワードがランダムに分散されている場合、クイックソートの平均時間が最も短くなります。
1. 挿入ソート - ストレート挿入ソート (ストレート挿入ソート)
ソートされた順序付きリストにレコードを挿入すると、レコード数が 1 増加した新しい順序付きリストが取得されます。つまり、まずシーケンスの最初のレコードを順序付けされたサブシーケンスとして扱い、次にシーケンス全体が順序付けされるまで 2 番目のレコードを 1 つずつ挿入します。
重要なポイント: 一時的な保存と配列境界の判断のためにセンチネルを設定します。 直接挿入による並べ替えの例:#挿入された要素と等しい要素が見つかった場合、挿入された要素によって目的の要素が配置されます。等しい要素の後に挿入します。したがって、等しい要素の順序は変化せず、元の順序なしシーケンスからの順序がソート後の順序になります。
# アルゴリズムの実装:
void print(int a[], int n ,int i){
cout<<i <<":";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void InsertSort(int a[], int n)
{
for(int i= 1; i<n; i++){
if(a[i] < a[i-1]){ //若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入
int j= i-1;
int x = a[i]; //复制为哨兵，即存储待排序元素
a[i] = a[i-1]; //先后移一个元素
while(x < a[j]){ //查找在有序表的插入位置
a[j+1] = a[j];
j--; //元素后移
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i); //打印每趟排序的结果
}
}
int main(){
int a[8] = {3,1,5,7,2,4,9,6};
InsertSort(a,8);
print(a,8,8);
}
2. 挿入ソート - ヒル ソート (シェルズ ソート)
基本的な考え方:
最初に、直接挿入ソートでは、ソート対象のレコード シーケンス全体がいくつかのサブシーケンスに分割され、シーケンス全体のレコードが「基本的に順序どおり」の場合、すべてのレコードが直接挿入されてソートされます。
操作方法:
インクリメンタルシーケンス t1、t2、...、tk を選択します。ここで、ti> tj , tk=1;
増分シーケンス番号 k に従ってシーケンスを k 回並べ替えます;
対応する順序に従って毎回並べ替えます増分 ti は、ソート対象の列を長さ m のいくつかのサブシーケンスに分割し、各サブテーブルに対して直接挿入ソートを実行します。インクリメント係数が 1 の場合のみ、シーケンス全体がテーブルとして処理され、テーブルの長さがシーケンス全体の長さになります。
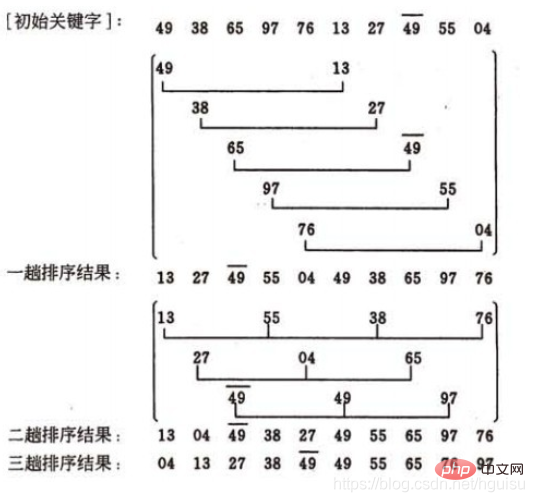
ヒル ソートの例:
シェル ソートのソート プロセスソート対象のファイルに 10 件のレコードがあり、そのキーワードが：49、38、65、97、76、13、27、49、55、04。 増分シリーズの値: 5、3、1
アルゴリズムの実装:
インクリメンタル シーケンスを単純に処理します。インクリメンタル シーケンス d = {n/2,n/4, n/8...1} n はソートされる数値の数ですつまり、まず、ソート対象のレコードのグループを、特定の増分 d (n/2、n はソート対象の数) に従っていくつかのサブシーケンスのグループに分割し、各グループ内のレコードの添字は d だけ異なります。グループごとに、すべての要素に対して直接挿入ソートを実行し、より小さい増分 (d/2) でグループ化して、各グループに対して直接挿入ソートを実行します。増分が 1 になるまで減分を続け、最後に直接挿入ソートを使用してソートを完了します。
void print(int a[], int n ,int i){
cout<<i <<":";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 直接插入排序的一般形式
*
* @param int dk 缩小增量，如果是直接插入排序，dk=1
*
*/
void ShellInsertSort(int a[], int n, int dk)
{
for(int i= dk; i<n; ++i){
if(a[i] < a[i-dk]){ //若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入
int j = i-dk;
int x = a[i]; //复制为哨兵，即存储待排序元素
a[i] = a[i-dk]; //首先后移一个元素
while(x < a[j]){ //查找在有序表的插入位置
a[j+dk] = a[j];
j -= dk; //元素后移
}
a[j+dk] = x; //插入到正确位置
}
print(a, n,i );
}
}
/**
* 先按增量d（n/2,n为要排序数的个数进行希尔排序
*
*/
void shellSort(int a[], int n){
int dk = n/2;
while( dk >= 1 ){
ShellInsertSort(a, n, dk);
dk = dk/2;
}
}
int main(){
int a[8] = {3,1,5,7,2,4,9,6};
//ShellInsertSort(a,8,1); //直接插入排序
shellSort(a,8); //希尔插入排序
print(a,8,8);
}希尔排序时效分析很难，关键码的比较次数与记录移动次数依赖于增量因子序列d的选取，特定情况下可以准确估算出关键码的比较次数和记录的移动次数。目前还没有人给出选取最好的增量因子序列的方法。增量因子序列可以有各种取法，有取奇数的，也有取质数的，但需要注意：增量因子中除1 外没有公因子，且最后一个增量因子必须为1。希尔排序方法是一个不稳定的排序方法。
基本思想：
在要排序的一组数中，选出最小（或者最大）的一个数与第1个位置的数交换；然后在剩下的数当中再找最小（或者最大）的与第2个位置的数交换，依次类推，直到第n-1个元素（倒数第二个数）和第n个元素（最后一个数）比较为止。
简单选择排序的示例：
操作方法：
第一趟，从n 个记录中找出关键码最小的记录与第一个记录交换；
第二趟，从第二个记录开始的n-1 个记录中再选出关键码最小的记录与第二个记录交换；
以此类推.....
第i 趟，则从第i 个记录开始的n-i+1 个记录中选出关键码最小的记录与第i 个记录交换，
直到整个序列按关键码有序。
算法实现：
void print(int a[], int n ,int i){
cout<<"第"<<i+1 <<"趟 : ";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 数组的最小值
*
* @return int 数组的键值
*/
int SelectMinKey(int a[], int n, int i)
{
int k = i;
for(int j=i+1 ;j< n; ++j) {
if(a[k] > a[j]) k = j;
}
return k;
}
/**
* 选择排序
*
*/
void selectSort(int a[], int n){
int key, tmp;
for(int i = 0; i< n; ++i) {
key = SelectMinKey(a, n,i); //选择最小的元素
if(key != i){
tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换
}
print(a, n , i);
}
}
int main(){
int a[8] = {3,1,5,7,2,4,9,6};
cout<<"初始值：";
for(int j= 0; j<8; j++){
cout<<a[j] <<" ";
}
cout<<endl<<endl;
selectSort(a, 8);
print(a,8,8);
}简单选择排序的改进——二元选择排序
简单选择排序，每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素（当前趟最大和最小记录）的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序，最多只需进行[n/2]趟循环即可。具体实现如下：
/** 这是伪函数, 逻辑判断不严谨
void selectSort(int r[],int n) {
int i ,j , min ,max, tmp;
for (i=1 ;i <= n/2;i++) {
// 做不超过n/2趟选择排序
min = i; max = i ; //分别记录最大和最小关键字记录位置
for (j= i+1; j<= n-i; j++) {
if (r[j] > r[max]) {
max = j ; continue ;
}
if (r[j]< r[min]) {
min = j ;
}
}
//该交换操作还可分情况讨论以提高效率
tmp = r[i-1]; r[i-1] = r[min]; r[min] = tmp;
tmp = r[n-i]; r[n-i] = r[max]; r[max] = tmp;
}
}
*/
void selectSort(int a[],int len) {
int i,j,min,max,tmp;
for(i=0; i<len/2; i++){ // 做不超过n/2趟选择排序
min = max = i;
for(j=i+1; j<=len-1-i; j++){
//分别记录最大和最小关键字记录位置
if(a[j] > a[max]){
max = j;
continue;
}
if(a[j] < a[min]){
min = j;
}
}
//该交换操作还可分情况讨论以提高效率
if(min != i){//当第一个为min值，不用交换
tmp=a[min]; a[min]=a[i]; a[i]=tmp;
}
if(min == len-1-i && max == i)//当第一个为max值，同时最后一个为min值，不再需要下面操作
continue;
if(max == i)//当第一个为max值，则交换后min的位置为max值
max = min;
if(max != len-1-i){//当最后一个为max值，不用交换
tmp=a[max]; a[max]=a[len-1-i]; a[len-1-i]=tmp;
}
print(a,len, i);
}
}堆排序是一种树形选择排序，是对直接选择排序的有效改进。
基本思想：
堆的定义如下：具有n个元素的序列（k1,k2,...,kn),当且仅当满足
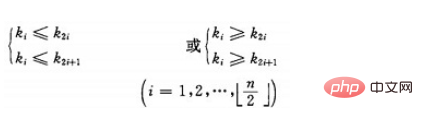
时称之为堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最小项（小顶堆）。
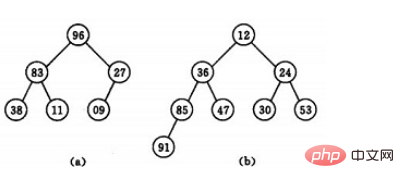
若以一维数组存储一个堆，则堆对应一棵完全二叉树，且所有非叶结点的值均不大于(或不小于)其子女的值，根结点（堆顶元素）的值是最小(或最大)的。如：
（a）大顶堆序列：（96, 83,27,38,11,09)
(b) 小顶堆序列：（12，36，24，85，47，30，53，91）
初始时把要排序的n个数的序列看作是一棵顺序存储的二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。
因此，实现堆排序需解决两个问题：
1. 如何将n 个待排序的数建成堆；
2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。
首先讨论第二个问题：输出堆顶元素后，对剩余n-1元素重新建成堆的调整过程。
调整小顶堆的方法：
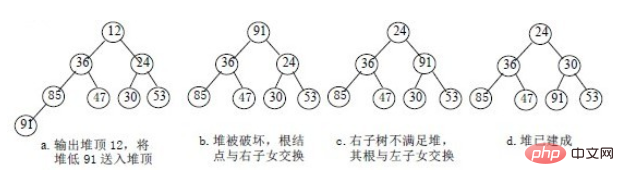
1）设有m 个元素的堆，输出堆顶元素后，剩下m-1 个元素。将堆底元素送入堆顶（（最后一个元素与堆顶进行交换），堆被破坏，其原因仅是根结点不满足堆的性质。
2）将根结点与左、右子树中较小元素的进行交换。
3）若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法 （2）.
4）若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法 （2）.
5）继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。
称这个自根结点到叶子结点的调整过程为筛选。如图：
再讨论对n 个元素初始建堆的过程。
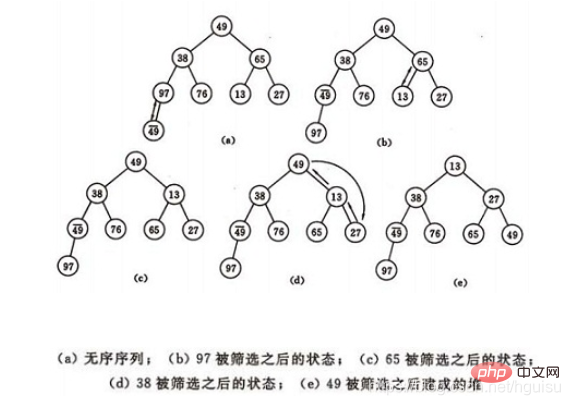
建堆方法：对初始序列建堆的过程，就是一个反复进行筛选的过程。
1）n 个结点的完全二叉树，则最后一个结点是第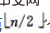
个结点的子树。
2）筛选从第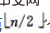个结点为根的子树开始，该子树成为堆。
3）之后向前依次对各结点为根的子树进行筛选，使之成为堆，直到根结点。
如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）
算法的实现：
从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
/**
* 已知H[s…m]除了H[s] 外均满足堆的定义
* 调整H[s],使其成为大顶堆.即将对第s个结点为根的子树筛选,
*
* @param H是待调整的堆数组
* @param s是待调整的数组元素的位置
* @param length是数组的长度
*
*/
void HeapAdjust(int H[],int s, int length)
{
int tmp = H[s];
int child = 2*s+1; //左孩子结点的位置。(i+1 为当前调整结点的右孩子结点的位置)
while (child < length) {
if(child+1 <length && H[child]<H[child+1]) { // 如果右孩子大于左孩子(找到比当前待调整结点大的孩子结点)
++child ;
}
if(H[s]<H[child]) { // 如果较大的子结点大于父结点
H[s] = H[child]; // 那么把较大的子结点往上移动，替换它的父结点
s = child; // 重新设置s ,即待调整的下一个结点的位置
child = 2*s+1;
} else { // 如果当前待调整结点大于它的左右孩子，则不需要调整，直接退出
break;
}
H[s] = tmp; // 当前待调整的结点放到比其大的孩子结点位置上
}
print(H,length);
}
/**
* 初始堆进行调整
* 将H[0..length-1]建成堆
* 调整完之后第一个元素是序列的最小的元素
*/
void BuildingHeap(int H[], int length)
{
//最后一个有孩子的节点的位置 i= (length -1) / 2
for (int i = (length -1) / 2 ; i >= 0; --i)
HeapAdjust(H,i,length);
}
/**
* 堆排序算法
*/
void HeapSort(int H[],int length)
{
//初始堆
BuildingHeap(H, length);
//从最后一个元素开始对序列进行调整
for (int i = length - 1; i > 0; --i)
{
//交换堆顶元素H[0]和堆中最后一个元素
int temp = H[i]; H[i] = H[0]; H[0] = temp;
//每次交换堆顶元素和堆中最后一个元素之后，都要对堆进行调整
HeapAdjust(H,0,i);
}
}
int main(){
int H[10] = {3,1,5,7,2,4,9,6,10,8};
cout<<"初始值：";
print(H,10);
HeapSort(H,10);
//selectSort(a, 8);
cout<<"结果：";
print(H,10);
}分析:
设树深度为k，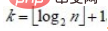
。从根到叶的筛选，元素比较次数至多2(k-1)次，交换记录至多k 次。所以，在建好堆后，排序过程中的筛选次数不超过下式：
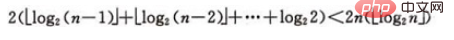
而建堆时的比较次数不超过4n 次，因此堆排序最坏情况下，时间复杂度也为：O(nlogn )。
基本思想：
在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。
冒泡排序的示例：
算法的实现：
void bubbleSort(int a[], int n){
for(int i =0 ; i< n-1; ++i) {
for(int j = 0; j < n-i-1; ++j) {
if(a[j] > a[j+1])
{
int tmp = a[j] ; a[j] = a[j+1] ; a[j+1] = tmp;
}
}
}
}冒泡排序算法的改进
对冒泡排序常见的改进方法是加入一标志性变量exchange，用于标志某一趟排序过程中是否有数据交换，如果进行某一趟排序时并没有进行数据交换，则说明数据已经按要求排列好，可立即结束排序，避免不必要的比较过程。本文再提供以下两种改进算法：
1．设置一标志性变量pos,用于记录每趟排序中最后一次进行交换的位置。由于pos位置之后的记录均已交换到位,故在进行下一趟排序时只要扫描到pos位置即可。
改进后算法如下:
void Bubble_1 ( int r[], int n) {
int i= n -1; //初始时,最后位置保持不变
while ( i> 0) {
int pos= 0; //每趟开始时,无记录交换
for (int j= 0; j< i; j++)
if (r[j]> r[j+1]) {
pos= j; //记录交换的位置
int tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
i= pos; //为下一趟排序作准备
}
}2．传统冒泡排序中每一趟排序操作只能找到一个最大值或最小值,我们考虑利用在每趟排序中进行正向和反向两遍冒泡的方法一次可以得到两个最终值(最大者和最小者) , 从而使排序趟数几乎减少了一半。
改进后的算法实现为:
void Bubble_2 ( int r[], int n){
int low = 0;
int high= n -1; //设置变量的初始值
int tmp,j;
while (low < high) {
for (j= low; j< high; ++j) //正向冒泡,找到最大者
if (r[j]> r[j+1]) {
tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;
}
--high; //修改high值, 前移一位
for ( j=high; j>low; --j) //反向冒泡,找到最小者
if (r[j]<r[j-1]) {
tmp = r[j]; r[j]=r[j-1];r[j-1]=tmp;
}
++low; //修改low值,后移一位
}
}基本思想：
1）选择一个基准元素,通常选择第一个元素或者最后一个元素,
2）通过一趟排序讲待排序的记录分割成独立的两部分，其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3）此时基准元素在其排好序后的正确位置
4）然后分别对这两部分记录用同样的方法继续进行排序，直到整个序列有序。
快速排序的示例：
（a）一趟排序的过程：
（b）排序的全过程
算法的实现：
递归实现：
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while(low < high){ //从表的两端交替地向中间扫描
while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索，至多到low+1 位置。将比基准元素小的交换到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void quickSort(int a[], int low, int high){
if(low < high){
int privotLoc = partition(a, low, high); //将表一分为二
quickSort(a, low, privotLoc -1); //递归对低子表递归排序
quickSort(a, privotLoc + 1, high); //递归对高子表递归排序
}
}
int main(){
int a[10] = {3,1,5,7,2,4,9,6,10,8};
cout<<"初始值：";
print(a,10);
quickSort(a,0,9);
cout<<"结果：";
print(a,10);
}分析：
快速排序是通常被认为在同数量级（O(nlog2n)）的排序方法中平均性能最好的。但若初始序列按关键码有序或基本有序时，快排序反而蜕化为冒泡排序。为改进之，通常以“三者取中法”来选取基准记录，即将排序区间的两个端点与中点三个记录关键码居中的调整为支点记录。快速排序是一个不稳定的排序方法。
快速排序的改进
在本改进算法中,只对长度大于k的子序列递归调用快速排序,让原序列基本有序，然后再对整个基本有序序列用插入排序算法排序。实践证明，改进后的算法时间复杂度有所降低，且当k取值为 8 左右时,改进算法的性能最佳。算法思想如下：
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while(low < high){ //从表的两端交替地向中间扫描
while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索，至多到low+1 位置。将比基准元素小的交换到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void qsort_improve(int r[ ],int low,int high, int k){
if( high -low > k ) { //长度大于k时递归, k为指定的数
int pivot = partition(r, low, high); // 调用的Partition算法保持不变
qsort_improve(r, low, pivot - 1,k);
qsort_improve(r, pivot + 1, high,k);
}
}
void quickSort(int r[], int n, int k){
qsort_improve(r,0,n,k);//先调用改进算法Qsort使之基本有序
//再用插入排序对基本有序序列排序
for(int i=1; i<=n;i ++){
int tmp = r[i];
int j=i-1;
while(tmp < r[j]){
r[j+1]=r[j]; j=j-1;
}
r[j+1] = tmp;
}
}
int main(){
int a[10] = {3,1,5,7,2,4,9,6,10,8};
cout<<"初始值：";
print(a,10);
quickSort(a,9,4);
cout<<"结果：";
print(a,10);
}基本思想：
归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
归并排序示例：
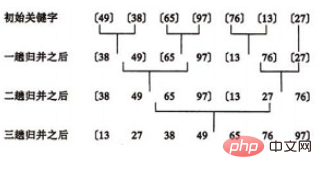
合并方法：
设r[i…n]由两个有序子表r[i…m]和r[m+1…n]组成，两个子表长度分别为n-i +1、n-m。
j=m+1；k=i；i=i; //置两个子表的起始下标及辅助数组的起始下标
若i>m 或j>n，转⑷ //其中一个子表已合并完，比较选取结束
//选取r[i]和r[j]较小的存入辅助数组rf
如果r[i]
//将尚未处理完的子表中元素存入rf
如果i<=m，将r[i…m]存入rf[k…n] //前一子表非空
如果j<=n , 将r[j…n] 存入rf[k…n] //后一子表非空
合并结束。
//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{
int j,k;
for(j=m+1,k=i; i<=m && j <=n ; ++k){
if(r[j] < r[i]) rf[k] = r[j++];
else rf[k] = r[i++];
}
while(i <= m) rf[k++] = r[i++];
while(j <= n) rf[k++] = r[j++];
}归并的迭代算法
1 个元素的表总是有序的。所以对n 个元素的待排序列，每个元素可看成1 个有序子表。对子表两两合并生成n/2个子表，所得子表除最后一个子表长度可能为1 外，其余子表长度均为2。再进行两两合并，直到生成n 个元素按关键码有序的表。
void print(int a[], int n){
for(int j= 0; j<n; j++){
cout<<a[j] <<" ";
}
cout<<endl;
}
//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{
int j,k;
for(j=m+1,k=i; i<=m && j <=n ; ++k){
if(r[j] < r[i]) rf[k] = r[j++];
else rf[k] = r[i++];
}
while(i <= m) rf[k++] = r[i++];
while(j <= n) rf[k++] = r[j++];
print(rf,n+1);
}
void MergeSort(ElemType *r, ElemType *rf, int lenght)
{
int len = 1;
ElemType *q = r ;
ElemType *tmp ;
while(len < lenght) {
int s = len;
len = 2 * s ;
int i = 0;
while(i+ len <lenght){
Merge(q, rf, i, i+ s-1, i+ len-1 ); //对等长的两个子表合并
i = i+ len;
}
if(i + s < lenght){
Merge(q, rf, i, i+ s -1, lenght -1); //对不等长的两个子表合并
}
tmp = q; q = rf; rf = tmp; //交换q,rf，以保证下一趟归并时，仍从q 归并到rf
}
}
int main(){
int a[10] = {3,1,5,7,2,4,9,6,10,8};
int b[10];
MergeSort(a, b, 10);
print(b,10);
cout<<"结果：";
print(a,10);
}两路归并的递归算法
void MSort(ElemType *r, ElemType *rf,int s, int t)
{
ElemType *rf2;
if(s==t) r[s] = rf[s];
else
{
int m=(s+t)/2; /*平分*p 表*/
MSort(r, rf2, s, m); /*递归地将p[s…m]归并为有序的p2[s…m]*/
MSort(r, rf2, m+1, t); /*递归地将p[m+1…t]归并为有序的p2[m+1…t]*/
Merge(rf2, rf, s, m+1,t); /*将p2[s…m]和p2[m+1…t]归并到p1[s…t]*/
}
}
void MergeSort_recursive(ElemType *r, ElemType *rf, int n)
{ /*对顺序表*p 作归并排序*/
MSort(r, rf,0, n-1);
}说基数排序之前，我们先说桶排序：
基本的な考え方: は、配列を限られた数のバケットに分割することです。各バケットは個別に並べ替えられます (他の並べ替えアルゴリズムを使用したり、再帰的な方法でバケットの並べ替えを使用し続けることも可能です)。バケット ソートは、鳩の穴ソートの帰納的な結果です。バケット ソートでは、ソート対象の配列内の値が均等に分散されている場合、線形時間 (Θ(n)) が使用されます。ただし、バケット ソートは比較ソートではないため、O(n log n) 下限の影響を受けません。
簡単に言うと、データをバケットにグループ化し、各バケット内の内容を並べ替えることを意味します。
たとえば、n 個の整数 A[1..n] を [1..1000] の範囲で並べ替える場合は、
まず、バケットを次の範囲に設定します。 10、具体的には、セット B[1] に [1..10] の整数を格納し、セット B[2] に (10..20] の整数を格納します。...セット B[i] を格納します ((i- 1)* 10, i*10] は整数です、i = 1,2,..100。バケットは合計 100 個あります。
次に、A[1..n] を最初から最後までスキャンします。 , そして、各 A[i] を対応するバケット B[j] に入れます。次に、これら 100 個の各バケット内の数値を並べ替えます。このとき、バブル、選択、さらにはクイック ソートを使用できます。一般的に、任意の
最後に、各バケット内の数値を順番に出力し、各バケット内の数値を小さい順に出力して、すべての数値がソートされた順序を取得します。 .
n 個の数値と m 個のバケットがあるとします。数値が均等に分散されている場合、各バケットには平均 n/m 個の数値が存在します。
が数値のクイック ソートを使用する場合各バケットでは、アルゴリズム全体の複雑さは O(n m * n/m*log(n/m)) = O(n nlogn - nlogm)
上の式から、 m がn に近い場合、バケットソートの複雑さは O(n) に近くなります
もちろん、上記の複雑さの計算は、入力 n 数値が均等に分散されているという前提に基づいています。この前提は非常に強力です。実際、 , 適用上の効果はあまり良くありません。すべての数値が同じバケットに分類されると、一般的な並べ替えに堕落します。
上記の主要な並べ替えアルゴリズムのほとんどの時間計算量は O(n2) です, 時間計算量が O(nlogn) のソート アルゴリズムもいくつかあります。バケット ソートでは O(n) 時間計算量を達成できます。ただし、バケット ソートの欠点は次のとおりです:
1) まず、空間計算量が比較的高いソートには 2 つの配列分のスペース オーバーヘッドがあり、1 つはソート対象の配列を格納するためのもので、もう 1 つはいわゆるバケットです。たとえば、ソート対象の値が 0 から m までの場合、 -1 の場合、m 個のバケットが必要です。このバケット配列には少なくとも m 個のスペースが必要です。
2) 次に、並べ替えられる要素は特定の範囲内にある必要があります。
バケット ソートは分散ソートです。割り当てソートの特別な点は、キー コードを比較する必要がないことですが、その前提として、ソートされる列の特定の条件がわかっている必要があります。
割り当てソートの基本的な考え方: 端的に言えば、複数のバケットによるソートを実行することです。
基数ソート プロセスでは、キーワードの比較は必要ありませんが、「割り当て」プロセスと「収集」プロセスを通じてソートが実装されます。それらの時間計算量は線形オーダー: O(n) に達する可能性があります。#例:
トランプの 52 枚のカードは、スーツと額面に応じて 2 つのフィールドに分けることができます。サイズの関係は次のとおりです: カラー:
プラム ブロッサム< ダイヤモンド< レッド ハート< ブラック ハート
額面: 
2 < ; 3 < 4 < 5 < 6 < 7 < 8 < 9 < 10 < J < Q < K < A
トランプの場合スートと額面で昇順にソートされます ソートして次の順序を取得します:
つまり 2 枚のカード スートが異なる場合は、額面に関係なく、下のスートのカードが上のスートのカードより小さい 同じスートの場合のみ 次に、大小関係は額面の大きさで決まります。これはマルチキーソートです。 
为得到排序结果，我们讨论两种排序方法。
方法1：先对花色排序，将其分为4 个组，即梅花组、方块组、红心组、黑心组。再对每个组分别按面值进行排序，最后，将4 个组连接起来即可。
方法2：先按13 个面值给出13 个编号组(2 号，3 号，...，A 号)，将牌按面值依次放入对应的编号组，分成13 堆。再按花色给出4 个编号组(梅花、方块、红心、黑心)，将2号组中牌取出分别放入对应花色组，再将3 号组中牌取出分别放入对应花色组，……，这样，4 个花色组中均按面值有序，然后，将4 个花色组依次连接起来即可。
设n 个元素的待排序列包含d 个关键码{k1，k2，…，kd}，则称序列对关键码{k1，k2，…，kd}有序是指：对于序列中任两个记录r[i]和r[j](1≤i≤j≤n)都满足下列有序关系：
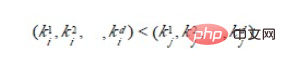
其中k1 称为最主位关键码，kd 称为最次位关键码 。
两种多关键码排序方法：
多关键码排序按照从最主位关键码到最次位关键码或从最次位到最主位关键码的顺序逐次排序，分两种方法：
最高位优先(Most Significant Digit first)法，简称MSD 法：
1）先按k1 排序分组，将序列分成若干子序列，同一组序列的记录中，关键码k1 相等。
2）再对各组按k2 排序分成子组，之后，对后面的关键码继续这样的排序分组，直到按最次位关键码kd 对各子组排序后。
3）再将各组连接起来，便得到一个有序序列。扑克牌按花色、面值排序中介绍的方法一即是MSD 法。
最低位优先(Least Significant Digit first)法，简称LSD 法：
1) 先从kd 开始排序，再对kd-1进行排序，依次重复，直到按k1排序分组分成最小的子序列后。
2) 最后将各个子序列连接起来，便可得到一个有序的序列, 扑克牌按花色、面值排序中介绍的方法二即是LSD 法。
基于LSD方法的链式基数排序的基本思想
“多关键字排序”的思想实现“单关键字排序”。对数字型或字符型的单关键字，可以看作由多个数位或多个字符构成的多关键字，此时可以采用“分配-收集”的方法进行排序，这一过程称作基数排序法，其中每个数字或字符可能的取值个数称为基数。比如，扑克牌的花色基数为4，面值基数为13。在整理扑克牌时，既可以先按花色整理，也可以先按面值整理。按花色整理时，先按红、黑、方、花的顺序分成4摞（分配），再按此顺序再叠放在一起（收集），然后按面值的顺序分成13摞（分配），再按此顺序叠放在一起（收集），如此进行二次分配和收集即可将扑克牌排列有序。
基数排序:
是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。
算法实现：
Void RadixSort(Node L[],length,maxradix)
{
int m,n,k,lsp;
k=1;m=1;
int temp[10][length-1];
Empty(temp); //清空临时空间
while(k<maxradix) //遍历所有关键字
{
for(int i=0;i<length;i++) //分配过程
{
if(L[i]<m)
Temp[0][n]=L[i];
else
Lsp=(L[i]/m)%10; //确定关键字
Temp[lsp][n]=L[i];
n++;
}
CollectElement(L,Temp); //收集
n=0;
m=m*10;
k++;
}
}各种排序的稳定性，时间复杂度和空间复杂度总结：
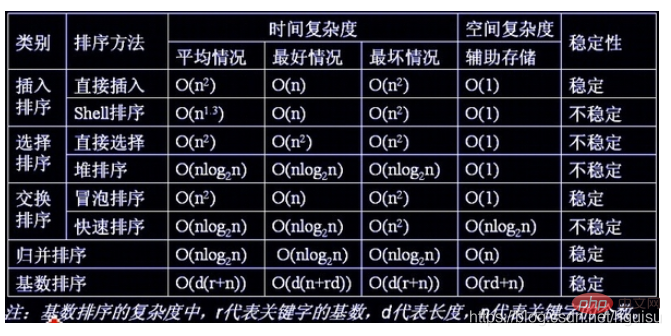
我们比较时间复杂度函数的情况：
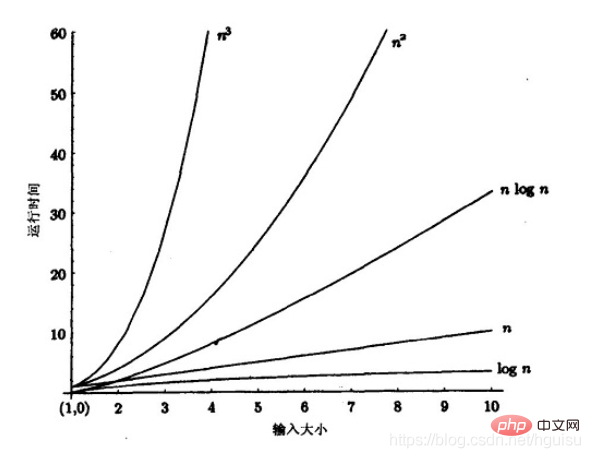
時間計算量関数 O(n) の増加
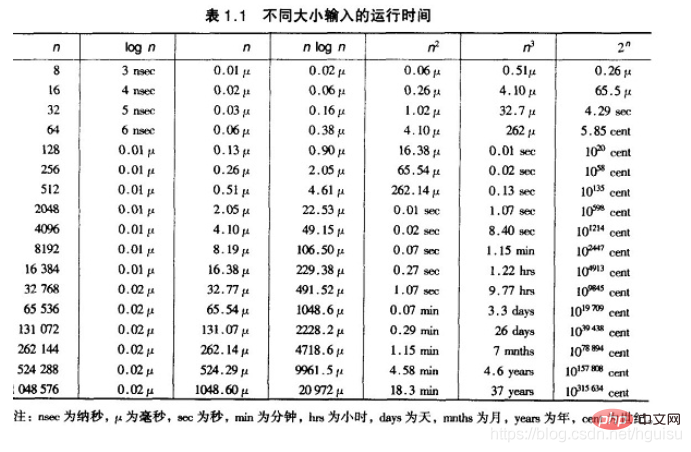
したがって、n が大きいレコードを並べ替えます。一般的に選択されるのは、時間計算量が O(nlog2n) のソート方法です。
時間計算量の観点:
(1) 平方オーダー (O(n2)) ソート
さまざまな種類の単純なソート: 直接挿入、直接選択、バブル ソート;
(2) 線形対数順序 (O(nlog2n)) ソート
クイック ソート、ヒープ ソート、マージ ソート;
(3)O(n1 §) ) sort、§ は 0 から 1 までの定数です。
ヒルソート
(4) 線形順序 (O(n)) ソート
バケットおよびボックスソートに加えてカーディナルソート。
注:
元のテーブルが順序付けされている場合、または基本的に順序付けされている場合、直接挿入ソートとバブル ソートを使用すると、比較とレコードの移動の数が大幅に削減され、時間の複雑さを O に減らすことができます。 (n);
クイック ソートはその逆です。元のテーブルが基本的に順序付けされている場合、バブル ソートに退化して、時間計算量が O(n2);
に増加します。元のテーブル Ordered は、単純な選択ソート、ヒープ ソート、マージ ソート、基数ソートの時間計算量にはほとんど影響しません。
#安定性:
#ソートアルゴリズムの安定性:Ifソートされるシーケンスに、 同じキーワード を持つ複数のレコードがあり、ソート後、これらのレコードの相対的な順序が変化しない場合、アルゴリズムは安定していると言われます。ソート後、レコードがそれらの相対的な順序が変化すると、アルゴリズムは不安定になると言われます。 安定性の利点
: 並べ替えアルゴリズムが安定している場合、あるキーで並べ替え、次に別のキーで並べ替えると、最初のキーによる並べ替えの結果が並べ替えに使用される 2 番目のキーになる可能性があります。基数ソートは次のようになります。最初に下位ビットでソートし、次に上位ビットでソートします。下位ビットが同じ要素の順序は、上位ビットが同じ場合は変わりません。さらに、ソート アルゴリズムが安定している場合は、冗長な比較を回避できます。
安定したソート アルゴリズム : バブル ソート、挿入ソート、マージ ソート、基数ソート
は安定したソート アルゴリズムではありません: 選択ソート、クイック ソート、ヒル ソート、ヒープ ソート
選択並べ替えアルゴリズムのガイドライン:
各並べ替えアルゴリズムには、独自の長所と短所があります。したがって、実際には、さまざまな状況に応じて適切に選択する必要があり、複数の方法を組み合わせることもできます。並べ替えアルゴリズム選択の基礎
並べ替えに影響を与える要因は多数あり、平均時間計算量が低いアルゴリズムが必ずしも最適であるとは限りません。 。逆に、特殊な場合には、平均時間計算量が高いアルゴリズムの方が適している場合もあります。同時に、アルゴリズムを選択する際には、ソフトウェアのメンテナンスを容易にするために、その可読性も考慮する必要があります。一般に、次の 4 つの要素を考慮する必要があります:
1.ソートされるレコード数 n のサイズ;
2。レコード自体のデータ量のサイズ、つまりキーワードを除くレコード内の他の情報のサイズ;
3.キーワードの構造と分布;
4.ソートの安定性の要件。
ソートする要素の数が n であるとします。1)
n が大きい場合、時間計算量は O( nlog2n ) ソート方法: クイック ソート、ヒープ ソート、またはマージ ソート。 クイック ソート: 現在、比較ベースの内部ソートの中で最良の方法と考えられています。ソート対象のキーワードがランダムに分散されている場合、クイック ソートの平均時間が最も短くなります。
ヒープ ソート:メモリ空間が許容し、安定性が必要な場合は、
マージ ソート: ある程度の量のデータ移動があるため、挿入ソートと組み合わせて、最初に一定の長さのシーケンスを取得してからそれをマージします。効率が向上します。
n が大きい場合、メモリ容量に余裕があり、安定性が必要 => マージソート
3)n が小さい場合、直接挿入または直接選択ソートを使用できます。 直接挿入ソート: 要素が順番に分散されている場合、直接挿入ソートは比較の数と移動レコードの数を大幅に削減します。
直接選択ソート: 要素は順番に分散されます。安定性が必要ない場合は、直接選択ソートを選択してください。
5) 通常は使用しないか、従来の方法を使用しません。直接泡立てて並べ替えます。 6)基数ソート プログラミング関連の知識について詳しくは、プログラミング入門をご覧ください。 ！
これは安定した並べ替えアルゴリズムですが、次のような制限があります。
1. キーワードは分解できます。
2. 記録されたキーワードの桁数は少ないため、密度が高い方が良いでしょう
3. 数値の場合は、符号なしが最適です。そうしないと、対応するマッピングの複雑さが増加します。まず追加または削除して、個別に並べ替えます。
以上が8 つの並べ替えアルゴリズムとは何ですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
