順番通りの走査はどのように実行されるのでしょうか?

インオーダートラバーサルのトラバーサル方法は次のとおりです。現在のノードについては、最初に左側のサブツリーをトラバースし、次に現在のノードにアクセスし、最後に右側のサブツリーをトラバースします。インオーダートラバーサルはバイナリツリートラバーサルの一種で、ミッドルートトラバーサルやインオーダーツアーとも呼ばれます。

このチュートリアルの動作環境: Windows 7 システム、C 17 バージョン、Dell G3 コンピューター。

二分木は重要なデータ構造であり、二分木を走査することも非常に重要です。ここでは、バイナリ ツリーを順番に走査する 3 つの方法を簡単に紹介します。バイナリ ツリーの順序トラバースでは、最初に左側のサブツリーをトラバースし、次に現在のノードにアクセスし、最後に右側のサブツリーをトラバースします。次のバイナリ ツリーの場合、順序トラバーサルの結果は次のようになります:

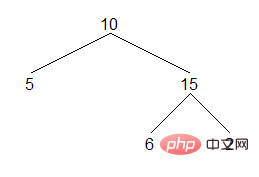
Result: [5,10,6,15,2]

直感的にわかるように、バイナリ ツリーの順序トラバーサルは、ノードを水平座標に投影することです。図に示すように:

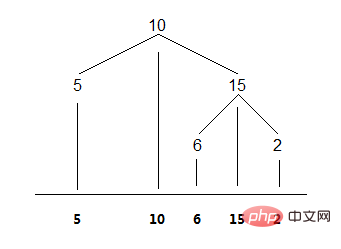
1. 再帰的メソッド

これは最も単純なメソッドであり、考えやすく、実装も簡単です。再帰の終了条件は、現在のノードが空かどうかです。最初に再帰呼び出しは左側のサブツリーをたどり、次に現在のノードにアクセスし、最後に右側のサブツリーが再帰的に呼び出されます。コードは次のとおりです:

//recursive
class Solution1 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        inorderHelper(ret,root);
        return ret;
    }
private:
    void inorderHelper(vector<int>& ret,TreeNode* root)
    {
        if(root==NULL)return;
        inorderHelper(ret,root->left);
        ret.push_back(root->val);
        inorderHelper(ret,root->right);
    }
};

2. 反復メソッド

反復メソッドでは、ルート ノードから開始してバイナリ ツリーの左端のノードを見つけ、渡されたノードをスタックに保存します。 , そして、一番左のノードを見つけます。ノードにアクセスした後、各ノードについて、それはそれ自体をルートとするサブツリーのルート ノードになります。訪問後、右の子に移動できます。コードは次のとおりです。

//iterate,using a stack
class Solution2 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        stack<TreeNode*> st;
        while(!st.empty()||curr!=NULL)
        {
            while(curr!=NULL)
            {
                st.push(curr);
                curr=curr->left;
            }
            curr=st.top();
            st.pop();
            ret.push_back(curr->val);
            curr=curr->right;
        }
        return ret;
    }
};

このメソッドの時間計算量は O(n) で、空間計算量も O(n) です。

3. モリスメソッド

このメソッドはモリスが発明したもので、読んでみて非常に絶妙だと感じました。このメソッドは再帰もスタックも使用せず、O(1) 空間計算量でバイナリ ツリーの走査を完了します。このメソッドの基本的な考え方は、右息子が NULL であるすべてのノードの右息子を後続ノードにポイントすることです (右息子が NULL ではないノードの場合、右息子が次にアクセスするノードになります)。このようにして、どのノードでも、アクセス後、その右側のノードが次に訪問するノードをポイントします。右端のノードの場合、そのような操作は必要ありません。この操作はトラバーサル中に完了し、ツリーはノード アクセスの完了後に復元されることに注意してください。ループ全体の判定条件は、現在のノードが空かどうかです。たとえば、上記のバイナリ ツリーでは、トラバーサル プロセスは次のようになります (現在のノード c の位置に基づく):

(1) 左の息子が空ではないため、現在のノードは 10 です。 c p の左側のサブツリーの右端のノードを見つけます:

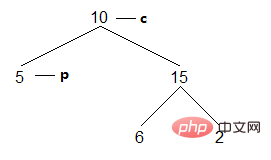
結果: []

(2) 2 つあります。ノード c の左のサブツリーの右端のノードを見つけるための終了条件。右の 1 つの息子は空で、右の 1 つの息子は現在のノードを指します。次は、右側の息子が空の場合です。このケースは、最初にノード p の右側の息子を後続ノード c にポイントしてから構築し、次に c を下に移動する必要があります。

# 結果: []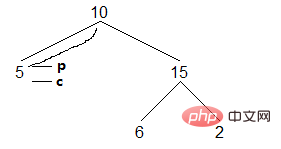
(3) 現在のノード c の左の息子は空です。アクセスします。アクセス後、c を右側の息子 (つまり、後継ノード) にポイントします:

結果: [5]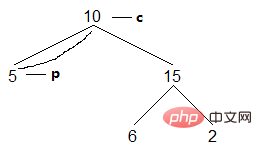
(4) 続行左のサブツリーを検索します。右端のノード。今回の終了条件は、右端のノードが現在のノードであることです。これは、現在のノードの左側のサブツリーが走査されたことを示しています。現在のノードにアクセスした後、バイナリ ツリーを復元し、現在のノードが後継ノードを指すようにします:

結果: [5,10 ]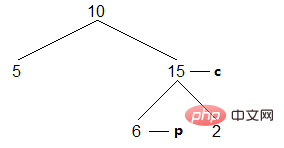
(5) c がバイナリ ツリー全体の右端のノードを指すまで、上記のプロセスを繰り返します:

左の息子は空です。アクセスすると、c が右の息子に進みます。右側の息子は空であり、判定条件を満たさないため、ループが終了し、トラバースが完了します。結果は次のようになります。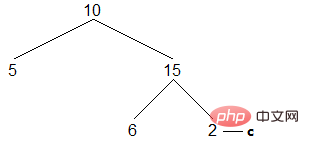
[5,10,6,15,2]

これはモリス法であり、時間計算量は O(n)、空間計算量は O です。 (1)。コードは次のとおりです:

//Morris traversal,without a stack
class Solution3 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                ret.push_back(curr->val);
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    ret.push_back(curr->val);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
};

推奨チュートリアル: "

C

#"

以上が順番通りの走査はどのように実行されるのでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。