はじめに:
実際、K-way マージ ソートは今でも非常に便利です。最も単純なものは、TB などの大量のデータを並べ替える場合です。 -レベルのデータ (TB レベルの検索キーワードとしましょう) ですが、メモリは GB レベルしかありません。一度にすべてのデータをロードして並べ替えることはできませんが、最終的には結果が必要なので、どうすればよいですか?する？ K-way マージソートがデビューします。実際、これは「分割統治」のアイデアです。Q 個の数値をソートしたいのですが、一度にすべてをソートすることはできません。このとき、Q を k に分割します。グループ、各グループは n.数値 (k 分析: (1) k 個のソートされた配列をマージするにはどうすればよいですか? ヒープについては以前に説明したので、明らかにヒープのソート効率は非常に高いので、当然ヒープを使用して実装することを検討しますが、昇順にソートする必要があるため、最小限のヒープを作成します。最終的な並べ替え結果の数値は常に前部で小さく、後部で大きいため、すべての n 配列の最初の要素 (最小数値) を最小ヒープに入れることを考慮し、最小ヒープのサイズは k になります。このようにしてヒープ構造を調整し、その最初の要素は min(min(array1),min(array2)....min(arrayn)) になります。これは明らかにすべての数値の中で最小の要素です。 (2) 配列は昇順に並べられているため、ヒープから最小限の要素を削除したら、その穴を埋める要素を見つけなければなりません。これを行うには、削除された要素が存在する配列内の次の要素を見つけて、それをヒープに埋める必要があります。 (これは、エリート連隊で戦うために国内で最もエリートな兵士を募集するのと似ています。その後、各連隊から最も強い者が採用されます。この人が不幸にして戦闘で死亡した場合、その人に次ぐ 2 番目の兵士を中隊から見つけます。では、削除されたヒープ要素に基づいて、削除されたヒープ要素が配置されている配列を見つけるにはどうすればよいでしょうか?これには、現在の値と、現在の値が配置されている配列の ID の両方を含む新しい複合型を作成する必要があります。 (3) ソートされた各配列は、最小の要素を持つため、まだソートに参加していない値は徐々に減少するため、長さ k の配列を維持する必要があります。この配列は、まだソートに参加していない各配列の現在位置を保持します。そして、配列内に残っている最小の要素がヒープに追加されると、現在の位置を後方に移動する必要があります。 (4) 各配列の現在位置が後方に移動すると、最終的には配列の末尾に到達します。この時点で、配列は数値を提供できなくなります (これは正常です。軍隊。鋭利なナイフ会社があり、そこには最も優秀な人材が集まっているので、最終的にエリート集団が選ばれるときは必ずこの会社から選ばれ、そしてこの会社には最終的には間違いなく誰もいないでしょう）現在削除されている番号が存在する配列からは見つけることができません。次の値に到達します。このとき、値を持つ次の配列 ID を選択し、その最小値を選択する必要があります。方法は arrayIdForDeletedData = (arrayIdForDeletedData 1) % k 。 (5) 最終的には、すべての配列位置は常に最後に到達します。つまり、すべての配列はソートに関与しない値を提供できないため、この時点で現在のヒープが存在するかどうかを判断する必要があります。そうでない場合は、空です。n*k の最大の数値が含まれています。最大の数値を小さい順に出力するために、deleteMin() を実行します。現在のヒープがすでに空の場合は、ループから直接抜け出します。 したがって、最終的な時間計算量はわずか O(n*logk)です。 コード: 上記の重要な技術的な詳細を明確に検討した後、ここでのコードは簡単に作成できます。 。 最初に、整数をカプセル化する値オブジェクトと、その整数がどの配列から取得されるかを定義します。 次に、問題とニーズを解決するための鍵となる最小ヒープを定義します。含まれる要素は上記の値オブジェクトである必要があることに注意してください。ヒープに入ってヒープを調整するとき、計算は値オブジェクトのデータ フィールドに基づいて行われます。 最後に、K-way コンバイナーを実装しましょう。これは実装が非常に簡単ですが、一部の添え字演算に関しては特別な注意が必要です。普遍的なものにしたいため、k と n の両方が渡されます。実際、k と n を事前に計画する場合、これらの数値を内部的に維持する必要はまったくありません。最小限の値に格納するだけでよいためです。ヒープ。 実験: 最後に、デモをしてみましょう。32 個の数値があるとします。それらを 4 つの結合方法に分割し、それぞれの方法に 8 つの数値があり、これら 8 つの数値はソートされています。 次に、K-way マージ アルゴリズムを使用して 32 個の数値すべてを並べ替えます: 最終的な実行結果は次のとおりです: 明らかに結果は正しく、このメソッドは重複した値をサポートしています。 package com.charles.algo.kwaymerge;
/**
*
* 这个对象表明是一个可以跟踪来自于哪个数组的数据对象
* @author charles.wang
*
*/
public class TrackableData {
//data表明具体的值
private int data;
//comeFromArray表明这个值来自于哪一个数组
private int comeFromArray;
public TrackableData(int data,int comeFromArray){
this.data = data;
this.comeFromArray=comeFromArray;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public int getComeFromArray() {
return comeFromArray;
}
public void setComeFromArray(int comeFromArray) {
this.comeFromArray = comeFromArray;
}
}package com.charles.algo.kwaymerge;
/**
* @author charles.wang
*
*/
public class MinHeap {
// 最小堆的存储是一个数组,并且为了计算，我们第一个位置不放内容
private TrackableData[] data;
// 堆的大小
private int heapSize;
// 当前元素的数量
private int currentSize;
public MinHeap(int maxSize) {
heapSize = maxSize;
// 创建一个比最大容纳数量多1的数组的作用是启用掉数组的头元素，为了方便运算，因为从1开始的运算更加好算
data = new TrackableData[heapSize + 1];
currentSize = 0;
}
/**
* 返回当前的堆是否为空
* @return
*/
public boolean isEmpty(){
if(currentSize==0)
return true;
return false;
}
/**
* 这里考察堆的插入，因为最小堆内部结构中数组前面元素总是按照最小堆已经构建好的，所以我们总从尾部插入 解决方法是： Step
* 1:先把当前的元素插入到数组的尾部 Step 2:递归的比较当前元素和父亲节点元素， Step
* 3:如果当前的元素小于父亲节点的元素，那么就把当前的元素上移，直到移不动为止
*
* @param value
* @return
*/
public MinHeap insert(TrackableData value) {
// 首先判断堆是否满了，如果满了就无法插入
if (currentSize == heapSize)
return this;
// 如果堆还没有满，那么说明堆中还有位置可以插入，我们先找到最后一个可以插入的位置
// currentPos表示当前要插入的位置的数组下标
int currentPos = currentSize + 1;
// 先插入到当前的位置，因为是从1开始的，所以数组下标运算也要+1
data[currentPos] = value;
// 然后比较当前元素和他的父亲元素
// 当前元素是data[currentPos] ，父亲元素是 data[(currentPos/2],一直遍历到根
TrackableData temp;
// 如果currentPos为1，表明是插入的堆中第一个元素，则不用比较
// 否则， 如果插了不止一个元素，则用插入位置的元素和其父元素比较
while (currentPos > 1) {
// 如果当前元素小于父亲元素，那么交换他们位置
if (data[currentPos].getData() < data[currentPos / 2].getData()) {
temp = data[currentPos / 2];
data[currentPos / 2] = data[currentPos];
data[currentPos] = temp;
// 更新当前位置
currentPos = currentPos / 2;
}
// 否则， 在假定已有的堆是最小堆的情况下，说明现在插入的位置是正确的，不用变换
else {
break;
}
}
// 插入完毕之后，吧当前的堆中元素的个数加1
currentSize++;
return this;
}
/**
* 这里考察堆的删除 因为是最小堆，所以肯定删除最小值就是删除堆的根元素，此外，还必须要调整剩余的堆使其仍然保持一个最小堆
* 因为有删除最小元素之后最小元素位置就有了个空位，所以解决方法是： Step 1:吧堆中最后一个元素复制给这个空位 Step
* 2:依次比较这个最后元素值，当前位置的左右子元素的值，从而下调到一个合适的位置 Step 3:从堆数组中移除最后那个元素
*/
public TrackableData deleteMin() {
// 如果最小堆已经为空，那么无法删除最小元素
if (currentSize == 0)
return null;
// 否则堆不为空，那么最小元素总是堆中的第一个元素
TrackableData minValue = data[1];
// 既然删除了最小元素，那么堆中currentSize的尺寸就要-1，为此，我们必须为数组中最后一个元素找到合适的新位置
// 堆中最后一个元素
TrackableData lastValue = data[currentSize];
// 先将堆中最后一个元素移动到最小堆的堆首
data[1] = lastValue;
// 把堆内部存储数组的最后一个元素清0
data[currentSize] = null;
// 并且当前的堆的尺寸要-1
currentSize--;
// 现在开始调整堆结构使其仍然为一个最小堆
int currentPos = 1; // 当前位置设置为根，从根开始比较左右
int leftPos = currentPos * 2;
TrackableData leftValue;
TrackableData rightValue;
TrackableData temp;
// 如果左位置和当前堆的总容量相同，说明只有2个元素了，一个是根元素，一个是根的左元素
if (leftPos == currentSize) {
// 这时候如果根左元素data[2]比根元素data[1]小，那么就交换二者位置
if (data[2].getData() < data[1].getData()) {
temp = data[2];
data[2] = data[1];
data[1] = temp;
}
}
else {
// 保持循环的条件是该节点的左位置小于当前堆中元素个数，那么该节点必定还有右子元素并且位置是左子元素位置+1
while (leftPos < currentSize) {
// 获取当前位置的左子节点的值
leftValue = data[leftPos];
// 获取当期那位置的右子节点的值
rightValue = data[leftPos + 1];
// 如果当前值既小于左子节点又小于右子节点，那么则说明当前值位置是正确的
if (data[currentPos].getData() < leftValue.getData()
&& data[currentPos].getData() < rightValue.getData()) {
break;
}
// 否则，比较左子节点和右子节点
// 如果左子节点小于右子节点（当然了，同时小于当前节点），那么左子节点和当前节点互换位置
else if (leftValue.getData() < rightValue.getData()) {
temp = data[currentPos];
data[currentPos] = leftValue;
data[leftPos] = temp;
// 同时更新当前位置是左子节点的位置,并且新的左子节点的位置为左子节点的左子节点
currentPos = leftPos;
leftPos = currentPos * 2;
}
// 如果右子节点小于左子节点(当然了，同时小于当前节点），那么右边子节点和当前节点互换位置
else {
temp = data[currentPos];
data[currentPos] = rightValue;
data[leftPos + 1] = temp;
// 同时更新当前位置是右子节点的位置,并且新的左子节点的位置为右子节点的左子节点
currentPos = leftPos + 1;
leftPos = currentPos * 2;
}
}
}
return minValue;
}
}package com.charles.algo.kwaymerge;
import java.util.ArrayList;
import java.util.List;
/**
*
* 这个类用于演示K路合并
*
* @author charles.wang
*
*/
public class KWayMerger {
private KWayMerger() {
}
/**
* k路合并，这里的指导思想如下：
*
* (1)首先构造一个最小堆，其中堆中的元素初始值为每个数组中的最小元素
* (2)每次从最小堆中打印并且删除最小元素，然后把这个最小元素所在的数组中的下一个元素插入到最小堆中 (3)每次（2）结束后调整堆来维持这个最小堆
*/
public static void mergeKWay(int k, int n, List<int[]> arrays) {
// 这里存储了所有每个数组的当前的下标,在没有开始插入之前，每个数组的当前下标都设为0
int[] indexInArrays = new int[k];
for (int i = 0; i < k; i++) {
indexInArrays[i] = 0;
}
// 首先构造一个最小堆,其大小为k
MinHeap minHeap = new MinHeap(k);
// 第一步，依次吧每个数组中的第一个元素都插入到最小堆
// 然后把所有数组的下标都指向1
for (int i = 0; i < k; i++) {
// 这里每个都构造TrackableData对象：
// 其中：arrays.get(i)[0]表示它值为第i个数组的下标为0的元素（也就是第i个数组的第一个元素）
// i表示这个对象来自于第i个数组
minHeap.insert(new TrackableData(arrays.get(i)[0], i));
indexInArrays[i] = 1;
}
// 第二步，对最小堆进行反复的插入删除动作
TrackableData currentDeletedData;
TrackableData currentInsertedData;
int arrayIdForDeletedData;
int nextValueIndexInArray;
// 循环的条件是k个数组中至少有一个还有值没有被插入到minHeap中
while (true) {
// 这个变量维护了有多少个数组当前下标已经越界，也就是数组所有元素已经被完全处理过
int noOfArraysThatCompletelyHandled = 0;
// 就是去查询维护所有数组当前下标的数组，如果都越界了，那么就说明都比较过了
for (int i = 0; i < k; i++) {
if (indexInArrays[i] == n)
noOfArraysThatCompletelyHandled++;
}
// 如果所有的数组中的所有的值都比较过了，那么查看堆中内容是否为空。
if (noOfArraysThatCompletelyHandled == k) {
while (!minHeap.isEmpty()) {
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
}
break;
}
currentDeletedData = minHeap.deleteMin();
// 打印出当前的数
System.out.print(currentDeletedData.getData() + " ");
// 获取当前的被删的数来自于第几个数组
arrayIdForDeletedData = currentDeletedData.getComeFromArray();
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
// 如果当前下标没有越界，说明当前数组中还有元素，则找到该数组中的下个元素
if (nextValueIndexInArray < n) {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
}
// 如果当前下标已经越界，说明这个数组已经没有任何元素了，则找下一个有值的数组的最小元素
else {
while (true) {
arrayIdForDeletedData = (arrayIdForDeletedData + 1) % k;
// 获取那个数组的当前下标
nextValueIndexInArray = indexInArrays[arrayIdForDeletedData];
if (nextValueIndexInArray == n)
continue;
else {
// 构造新的TrackableData，并且插入到最小堆
currentInsertedData = new TrackableData(
arrays.get(arrayIdForDeletedData)[nextValueIndexInArray],
arrayIdForDeletedData);
minHeap.insert(currentInsertedData);
// 同时更新维护数组当前下标的数组，让对应数组的当前下标+1
indexInArrays[arrayIdForDeletedData]++;
break;
}
}
}
}
}
}public static void main(String[] args) {
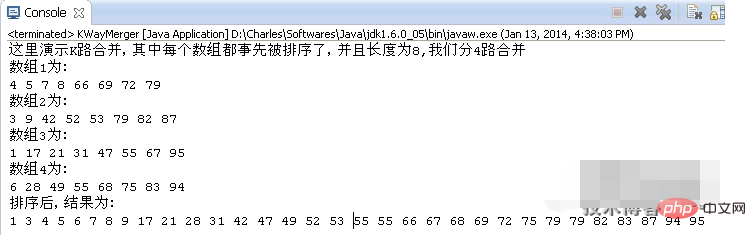
// 我们来演示K路合并，假设我们有4组已经排序了的数组，每组有8个数，则n=8,k=4
int[] array1 = { 4, 5, 7, 8, 66, 69, 72, 79 };
int[] array2 = { 3, 9, 42, 52, 53, 79, 82, 87 };
int[] array3 = { 1, 17, 21, 31, 47, 55, 67, 95 };
int[] array4 = { 6, 28, 49, 55, 68, 75, 83, 94 };
System.out.println("这里演示K路合并，其中每个数组都事先被排序了，并且长度为8,我们分4路合并");
System.out.println("数组1为：");
for(int i=0;i<array1.length;i++)
System.out.print(array1[i]+" ");
System.out.println();
System.out.println("数组2为：");
for(int i=0;i<array2.length;i++)
System.out.print(array2[i]+" ");
System.out.println();
System.out.println("数组3为：");
for(int i=0;i<array3.length;i++)
System.out.print(array3[i]+" ");
System.out.println();
System.out.println("数组4为：");
for(int i=0;i<array4.length;i++)
System.out.print(array4[i]+" ");
System.out.println();
List<int[]> arrayLists = new ArrayList<int[]>(4);
arrayLists.add(0, array1);
arrayLists.add(1, array2);
arrayLists.add(2, array3);
arrayLists.add(3, array4);
KWayMerger kWayMerger = new KWayMerger(4, 8, arrayLists);
System.out.println("排序后，结果为：");
kWayMerger.mergeKWay();
System.out.println();
}
以上がK-wayマージソートの詳しい解説（実戦編）の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
