PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する-PHPチュートリアル-php.cn

昨日、飯能タワーのアルゴリズムを 1 日勉強しました。IQ が打ち砕かれたように感じました。「ゴリラボールの台頭」のオランウータンにも及びませんでした。！！

由来

この問題を最初に考案したのは、フランスの数学者「エドワード・ルーカス」だと言われています。

世界の中心にあるベナレス神殿（インド北部）には、真鍮の板に3本の宝石の針が差し込まれています。ヒンドゥー教の主神ブラフマー神が世界を創造したとき、大小合わせて64枚の金片を一本の針に下から上に通して作ったものが、いわゆるハノイの塔です。昼も夜も関係なく、僧侶が次のルールに従ってこれらの金貨を動かします。一度に 1 つの金貨だけを動かし、どの針の上にあるとしても、小さな金貨は大きな金貨の上に置かなければなりません。僧侶たちは、梵天が通した針から別の針にすべての金塊が移動すると、世界は雷鳴とともに滅び、バチカン塔、寺院、そしてすべての生き物も一緒に滅びると予言しました。

この伝説にはさまざまなバリエーションがあり、それが誰であるかは不明ですが、残された数学的問題は非常に古典的です。

彼が残した数学的知識:金片の数と移動ステップ数の関係は 2^n - 1 です。

金貨 1 枚の移動数は 2 の 1 乗マイナス 1 です。
金貨 2 枚の移動数は 2 の 2 乗マイナスです。 1
3 金駒の手数は 2 の 3 乗 - 1
金駒の手数 2 の n 乗は 1

伝説が真実であれば、僧侶たちはこのタスクを完了するのに 2^64 - 1

のステップが必要でした。彼らが 1 秒あたり 1 個の金貨を移動したと仮定すると、それにかかる時間は完了までに5,849億年。宇宙全体ができてからまだ 137 億年しか経っていないので、宇宙の滅亡にはまだ早いです... (暇なので下記のように計算してみました)

PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する

#基本ルール

ハノイ塔のアルゴリズムには、移動するプレートがプレートであると仮定した場合、2 つの基本条件があります。

1. 一度に移動できるプレートは 1 つだけです。
2. 小さな皿は大きな皿の上に置かれなければなりません。

分析

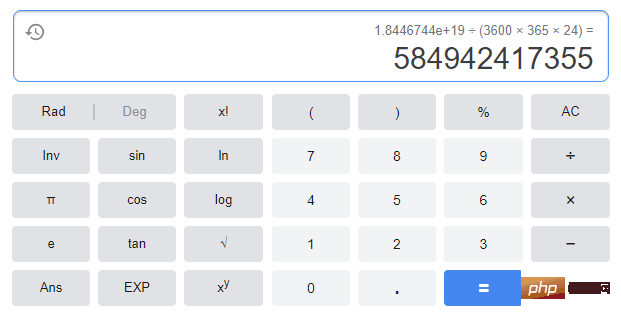
このゲームには、A、B、C という 3 つの柱があるとします。そのうちの 1 つにすでに N 個の並べ替えられたプレートがあり、最大のプレートが一番下にあり、プレートは上に行くにつれてどんどん小さくなり、他に 2 つの空の列があります。

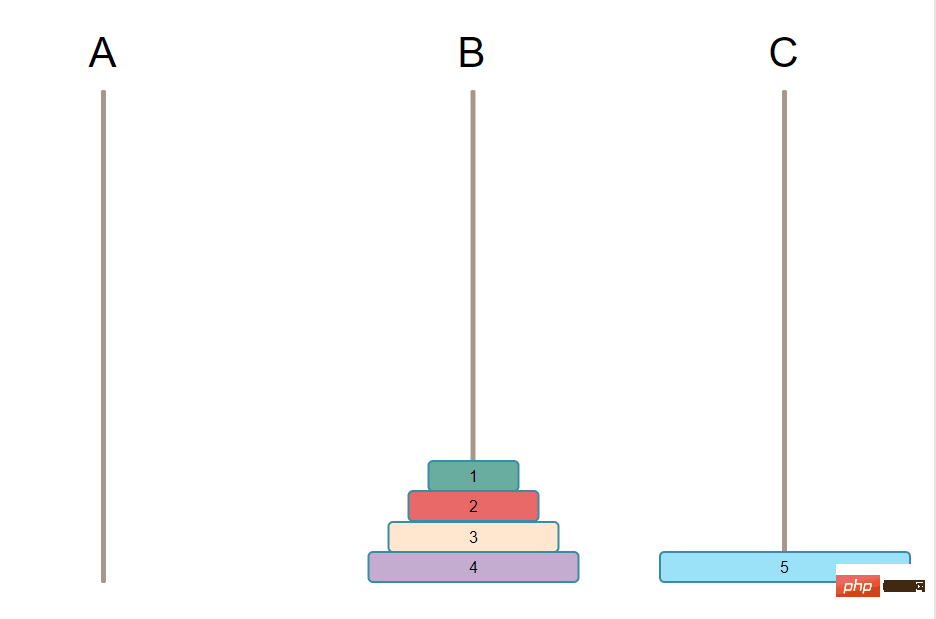
初期状態は次のとおりです。

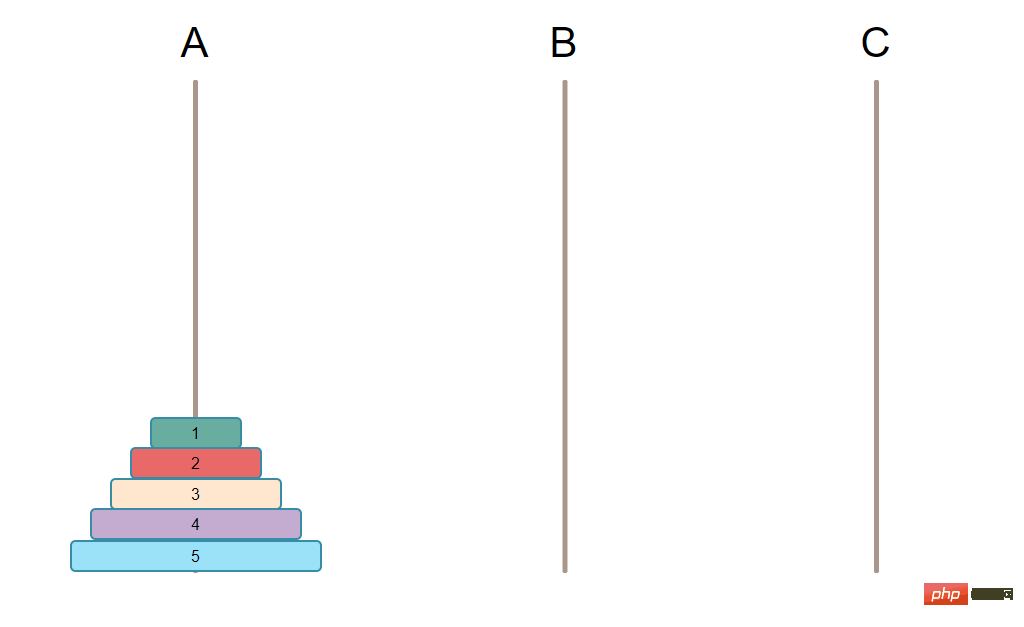
PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する

達成する必要がある最終目標は、柱上のすべてのプレートを別の柱に移動することです。 [推奨される学習: PHP ビデオチュートリアル ]

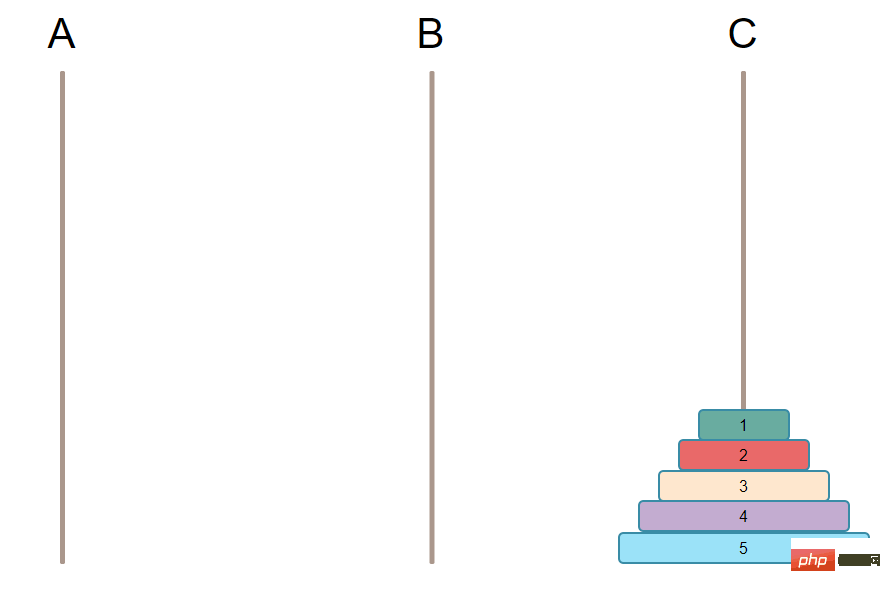
PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する

実装の一般的なアイデア:

何を捨てるか「各ステップの手順が非常に複雑です。私の頭の能力が足りないと思います。最初に最もシンプルで大雑把な解決ロジックを考えたいと思います。」
大きなプレートが一番下にあるという基本条件を満たすには、まず A の最大のプレートを空にし、次に最大のプレートを柱 C に置く必要があります。最大の皿番号を N とします。
C に移動したいので、最初のステップを達成するには、N-1 プレートを柱 B に移動する必要があります。この方法でのみ、N 番目のプレート (つまり、、最大のプレート）を柱 C に移動できます。
N-1 プレートを柱 B に移動します。条件を満たすには、大きなプレートが下に、小さなプレートが上にある必要があるため、これらの N-1 プレート B ピラーにも連続しています。
最後に、これらの N-1 プレートを柱 B から柱 C に移動して、最終目標を完了します。

要約:

最初のステップは、A 上の N-1 枚のプレートを B に移動することです。

最初に N-1 を B に移動する必要があるのはなぜですか?ご存知のとおり、最終的に達成するのは A から C にあるすべてのプレートを移動することなので、順序は変更できません。大きいプレートが一番下にあり、小さいプレートが一番上にあるだけです。次に、必ず最大のものを最初に C に移動する必要があります。そうしないと、条件が満たされません。

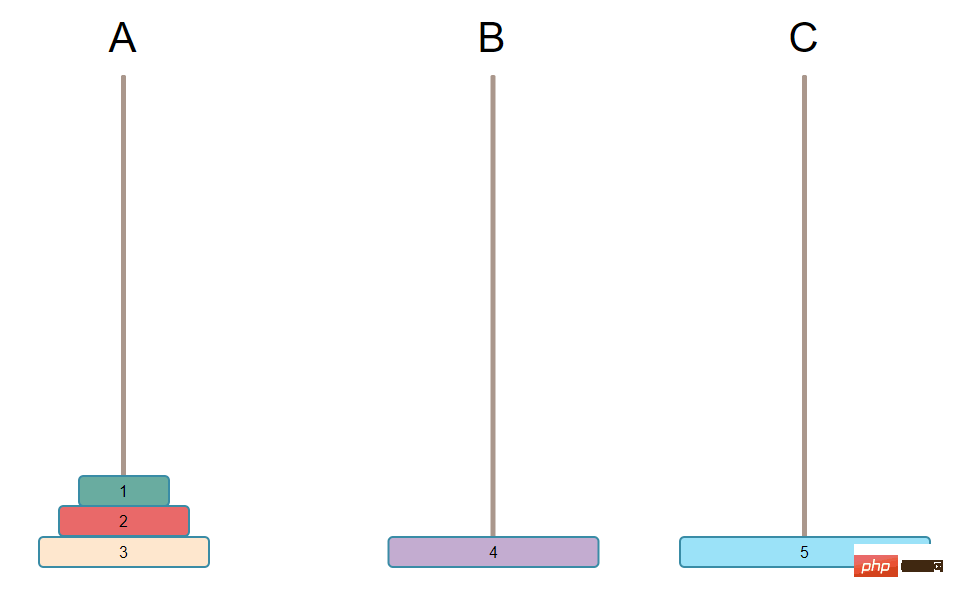
最大のプレートを A から C に移動するには、A の最大のプレートを空ける必要があります。つまり、最大のプレート上のすべてのプレートを移動する必要があります。そして、柱は 3 つしかありません。C には他のプレートハンドルがあってはなりません。そうでないと、再び条件を満たせません。これらの N-1 プレートはすべて B にのみ配置でき、まだ順番に配置されています。次の図のようになります。

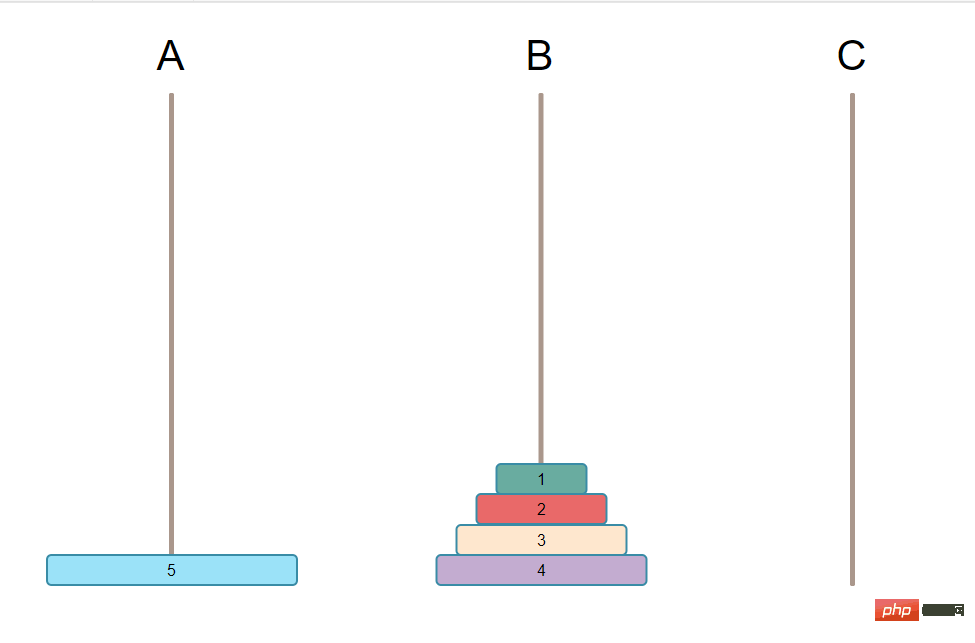
PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する

2 番目のステップは、A の N 番目のプレート (つまり、最大のプレート) を C に移動することです。

これは非常に簡単で、一度に最大のプレートを A から C に移動するだけです。以下に示すように:

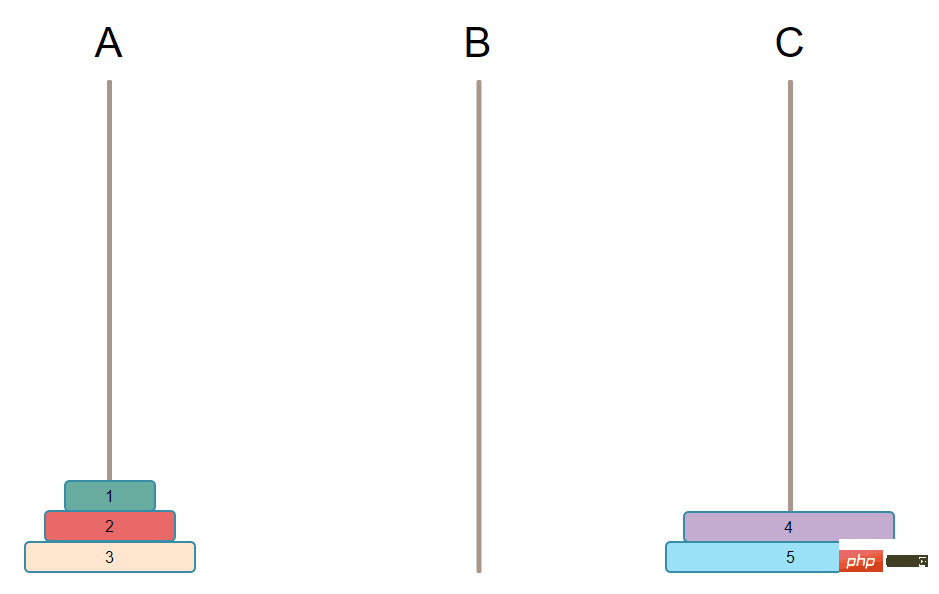
PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する

#3 番目のステップは、B 上の N-1 個のプレートを C に移動することです。

注: N-1 枚のプレートを C に移動するには、その中で最大のプレートを見つけて、その最大のプレートを最初に移動することになります。したがって、ここでは実際にはステップ 1 と 2 を繰り返し、N-1 個の中で最大のものを見つけて、それを最初に C に移動するというサイクルが繰り返されます。

3 番目のステップは、実際には要件を変更することに相当します。K = N - 1 と仮定します。

柱 B には K プレートがあり、柱 A は空で、柱 C には最大のプレートがあるため、K プレートのある柱 B の場合、空であることに相当します。
最初のステップは、B の K-1 プレートを A に移動することです。
2 番目のステップは、B の K 番目のプレートを C に移動することです。
3 番目のステップは、A の K-1 プレートを C に移動することです。

#下の写真になります

まず残ったプレートの中から一番大きなプレートを見つけます

次に一番大きなプレートを移動します

##その後、プレートが 1 枚だけ残るまでループし、C に直接移動するとゲームは終了です。

補助柱補助柱とは何ですか？移動したいすべてのプレートが A 上にあり、目標は C に移動することであると仮定すると、B は

N-1

プレートの補助柱になります。なぜなら、彼らは一時的にしかここに存在することができず、そうでなければゲームのルールを満たさないからです。ここでは、まず補助的な柱を見つける必要があります。それをどのように実装するかを考えるのではなく、まずロジックを明確にしてください。

A から B への移動を実現するには、C が補助柱です。

A から C への移動を実現するには、B が補助柱です。
To B から C に移動すると認識し、A が補助柱になります

実装上記の分析を通じて、これが実際には繰り返されていることがわかります。サイクル内の操作。これは再帰と非常に似ており、ここでのすべては再帰を使用して実装できます。

再帰を使用するには、2 つの必要な条件があります

1. 再帰式を見つけます

2. 終了条件を見つけます

終了条件書くのは簡単ですが、プレートが1枚の場合はCピラーに直接移動する必要があります。

それでは、漸化式とは何でしょうか?上記の論理分析に基づいて、それは 3 つのステップに分解できます。

最初のステップは、[N-1] プレートを A から B に移動することです

2 番目のステップは、[N 番目] プレートを A から C## に移動することです
#3 番目のステップは、[残りの N-1] プレートを B から C に移動することです。
以下は、PHP で実装された疑似コードです:

class HanoiTower
{
    // 计数器
    public $count = 0;
    /**
     * 汉诺塔实现
     * 
     * @param $n 盘子号
     * @param $A 初始柱子
     * @param $B 中转站
     * @param $C 目标柱子
     */
    public function hanoi($n, $A, $B, $C)
    {
        if ($n == 1) {
            // 退出条件 只剩一个盘子的时候直接从A移动到C
            $this->biggestOne($n, $A, $B, $C);
        } else {
            // PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する把 【n-1】 个盘子从A移动到B 此时C为中转站
            $this->hanoi($n - 1, $A, $C, $B);
            // PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する把 【第n】 个盘子从A移动到C
            $this->biggestOne($n, $A, $B, $C);
            // 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
            $this->hanoi($n - 1, $B, $A, $C);
        }
    }
    /**
     * 移动最大的盘子
     * 直接从A移动到C
     */
    public function biggestOne($n, $A, $B, $C)
    {
        ++$this->count;
        echo &#39;第&#39;, $this->count, &#39;步 &#39;, &#39;把 &#39;, $n, &#39;从 &#39;, $A, &#39;移动到&#39;, $C, &#39;<br />&#39;;
    }
}
$n = 5;
$hanoiTower = new HanoiTower();
echo &#39;这是一个有 【&#39;, $n, &#39;】 个盘子的汉诺塔：&#39;, &#39;<br />&#39;;
// 调用执行
$hanoiTower->hanoi($n, &#39;A&#39;, &#39;B&#39;, &#39;C&#39;);
echo &#39;总共需要走：【&#39;, $hanoiTower->count, &#39;】 步&#39;;

ログイン後にコピー

結果は次のようになります:

PHP が興味深いハノイ塔アルゴリズムをどのように実装するかを分析する