完全二分木と手がかり付き二分木とは何ですか?シーケンシャルストレージ構造はどのようなものですか?

前回の記事では、バイナリ ツリーの基本的なチェーン構造と、ツリーの構築とトラバースに関連する操作について学習しました。今日、私たちはバイナリ ツリーとバイナリ ツリーの修正された形式に関連するいくつかの概念を学びます。

完全なバイナリ ツリー

完全なバイナリ ツリーとは何ですか?完全なバイナリ ツリーについて話す前に、「完全なバイナリ ツリー」という別の用語について話しましょう。前回の記事で示したようなバイナリ ツリーは「完全バイナリ ツリー」です。このツリーでは、すべてのノードに 2 つの子ノードがあり、子ノードが 1 つだけのノードはなく、最下位のリーフ ノードはすべて同じレベルにあります。この種のツリーは「フル バイナリ ツリー」と呼ばれ、「パーフェクト バイナリ」とも呼ばれます。木"。

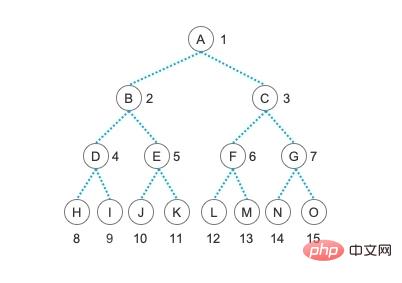
とても美しい木ですね。はい、この種の二分木は非常に完璧で、余分なノードや欠落したノードがなく、非常に美しいです。しかし、実際には完璧なものは非常にまれであり、人生には常にいくつかの欠点があります。私たちは自分に欠点が多すぎないように努めますが、欠点のない人生を送ることは決してできません。したがって、リーフ ノードが最下位レベルとその次の下位レベルに出現することを許可し、最下位レベルのリーフ ノードはツリーの左側の部分に集中します、つまり、リーフ ノードは左側のサブツリーのみを持つことができます。このような少し欠けた木を「完全二分木」と呼びます。完璧でないことを心配する必要はありません。そのようなわずかな不完全さがあっても人生は完全なので、「完全な二分木」は理想的なツリー構造です。

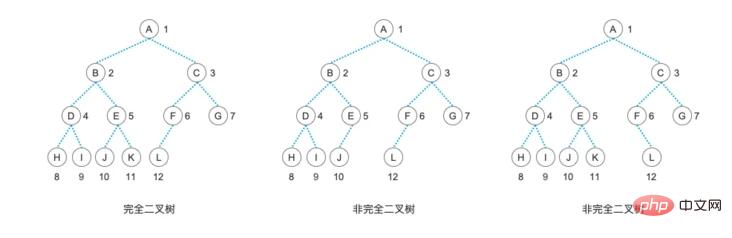
定義から、「完全なバイナリ ツリー」は「完全なバイナリ ツリー」でなければならず、リーフ ノードはすべて 1 つのレベルにあることがわかります。すべてのノードが左右の子ノードを持つ「二分木」も「完全二分木」です。

なぜ「完全なバイナリ ツリー」と「完全なバイナリ ツリー」について説明するのでしょうか?もちろん、それは次のコンテンツへの道を開くためです。 「完全なバイナリ ツリー」はバイナリ ツリーの特性に最もよく適合するツリーであるためです。ツリー シリーズの最初の記事で紹介したバイナリ ツリーの 5 つのプロパティをまだ覚えていますか?その際は「フルバイナリツリー」を例にして説明しました。その中で、プロパティ 5 は、バイナリ ツリーを格納するために逐次構造を使用する方法を学ぶための基礎です。

バイナリ ツリーのシーケンシャル ストレージ

「フル バイナリ ツリー」の概念とバイナリ ツリーのプロパティ 5 を通じて、シーケンシャル構造を格納するための配列の使用を実装できます。

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O'];

ご存知かと思いますが、前の記事では、この配列を使用してチェーン ツリーを構築しましたが、この配列は実際には線形に格納されたバイナリ ツリーです。二分木の性質5を比較して見てみましょう。

• ノード A の添え字は 1 で、これがツリーのルートです。その子ノードは B と C で、対応する添字はそれぞれ 2 と 3、つまり 1 2 と 1 2 1 です。

• 同様に、別のノード F を選択します。その添字は 6 であるため、左の子ノードの添字は 6 2 = 12 (L に対応)、右の子ノードの添字は 6 2 1 = 13 (M に対応) です。

• 逆に見ると、ノードの親ノードは i / 2 になります。 K ノードの添字が 11 で、その親ノードが 11 / 2 であることを見てみましょう。小数点を削除すると、添字 5 の位置、つまりノード E になります。ノード J の添字は 10 で、その親ノードは 11/2、ノードは 10 / 2、これもインデックス 5 の E ノードです。

これで、配列を使用してバイナリ ツリー構造を表す方法を誰もが理解できたと思います。さらに、配列の構造はより 1 次元であるため、ツリーの操作が 2 次元 1 次元表現、つまり非線形から線形への変換であることをよりよく反映できるため、これらを便利に操作できます。データ。

シーケンシャルストレージ構造、つまり配列要素の走査の場合、プレオーダー、ミッドオーダー、ポストオーダー、およびレイヤーオーダーの形式も使用できます。ただし、これらの走査メソッドは、バイナリ ツリーのプロパティ 5 に従って走査する必要があります。しかし、もっと重要なことは、添え字を与えてさえいれば、二分木のプロパティを通じて、その下位ノードと上位ノードの位置を簡単に知ることができ、これらのノードの情報をすぐに取得できることです。この主要な機能は、チェーン構造のバイナリ ツリーでは利用できません。

保存したいものが「完全なバイナリ ツリー」ではない場合はどうすればよいでしょうか?完全なバイナリ ツリーでなくても、対応するノードを null 値に設定するだけで済みます。例:

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

この木の構造に対応する二分木グラフは次のようになります:

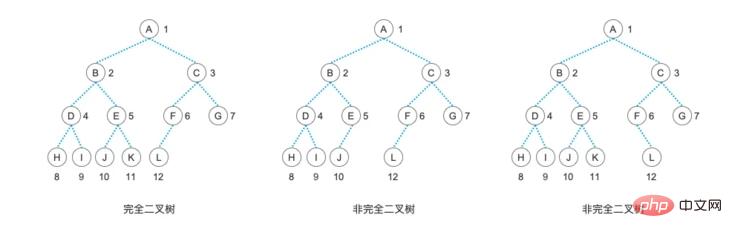
そして、チェーン ツリーを構築する方法では、必要なのは、もう 1 つの判断を追加するだけです。このように順次保存されたバイナリ ツリーを使用して連鎖バイナリ ツリーを迅速に生成でき、その後の操作が容易になります。

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

手掛かりバイナリ ツリー

別のリンクの中の 1 つのリンク、次に「手掛かりバイナリ ツリー」について話しましょう。これは何ですか？

从上面的学习中，我们知道了”满二叉树“和”完全二叉树“。但是这种结构都是非常理想的树结构，不过真实的情况可能大部分都是”理想很丰满，现实很骨感“。很多树并不能形成那样的完全二叉树的形式，更别提”满二叉树“了。而树的遍历又经常会使用栈或者队列来实现，这两种遍历方式基本都是线性的，也就是最好情况下也是 O(n) 的时间复杂度。那么，有没有什么更快一点的方式来提高遍历的效率呢？

我们这样来尝试一下：

• 如果树的叶子结点的左孩子结点为空，就让它指向前驱（上级）结点

• 如果树的叶子结点的右孩子结点为空，就让它指向后继结点

这样有什么好处呢？我们可以避免掉大范围的递归操作，从而加快树的遍历速度。在整个算法中，它并没有什么优势，因为我们需要将一颗树进行线索化，也就是去改变它的叶子结点的左右孩子的指向，这也是一次遍历。但是，如果你的操作是经常需要遍历，而且是来回的多次遍历，那么它的整体性能是要强于普通二叉树的遍历的。因为在一次线索化之后，它的遍历就是在快速的查找叶子结点的基础上进行普通的线性遍历操作，而不是递归操作。

对于线索二叉树来说，我们需要改变树的结点存储数据结构。

// 线索二叉树结点
class TBTNode
{
    public $data;
    public $lTag = 0;
    public $rTag = 0;
    public $lChild;
    public $rChild;
}

我们增加了两个标志位，当 $lTag 或 $rTag 为 1 时，$lChild 或 $rChild 分别指向前驱或后继结点。这样在最后的遍历时，我们就可以快速地通过这个 tag 标志位分辨出结点的指向状态。

然后我们先简单地建立一颗树。使用上一节中的那个示例。

// 建立二叉树
function CreateBiTree($arr, $i)
{
    if (!isset($arr[$i]) || !$arr[$i]) { // 这里增加了个判断，如果数组元素为空
        return null;
    }
    $t = new TBTNode();
    $t->data = $arr[$i];
    $t->lChild = CreateBiTree($arr, $i * 2);
    $t->rChild = CreateBiTree($arr, $i * 2 + 1);
    return $t;
}

$treeList = ['', 'A', 'B', 'C', 'D', 'E', 'I', '', '', '', '', 'H', '', 'J', '', ''];

$tree = CreateBiTree($treeList, 1);

接下来就是最重要的线索化过程，我们可以建立前序、中序、后序的线索二叉树。对应的，在最后的线索二叉树遍历时获得的结果也将是这三种遍历方式所对应的结果。在这里，我们学习最普遍的也是最经典的”中序线索二叉树“。所以，我们以中序遍历的形式将这颗树线索化。

// 线索化
function InThread(?TBTNode $p, ?TBTNode &$pre)
{
    if ($p) {
        // 递归，左子树线索化
        InThread($p->lChild, $pre);

        if (!$p->lChild) {
            // 建立当前结点的前驱线索
            $p->lChild = $pre;
            $p->lTag = 1;
        }
        if ($pre && !$pre->rChild) {
            // 建立当前结点的后继线索
            $pre->rChild = $p;
            $pre->rTag = 1;
        }
        $pre = $p; // $pre 指向当前的 $p ，作为 $p 将要指向的下一个结点的前驱结点指示指针
        $p = $p->rChild; // $p 指向一个新结点，此时 $pre 和 $p 分别指向的结点形成了一个前驱后继对，为下一次线索化做准备
        
        // 递归，右子树线索化
        InThread($p, $pre);
    }
}

// 创建线索二叉树
function createInThread(TBTNode $root)
{
    $pre = null; // 前驱结点指针
    if($root){
        InThread($root, $pre);
        $pre->rChild = null; // 非空二叉树，线索化
        $pre->rTag = 1; // 后处理中序最后一个结点
    }
}

createInThread($tree);

var_dump($tree);
// object(TBTNode)#1 (5) {
//     ["data"]=>
//     string(1) "A"
//     ["lTag"]=>
//     int(0)
//     ["rTag"]=>
//     int(0)
//     ["lChild"]=>
//     object(TBTNode)#2 (5) {
//       ["data"]=>
//       string(1) "B"
//       ["lTag"]=>
//       int(0)
//       ["rTag"]=>
//       int(0)
//       ["lChild"]=>
//       object(TBTNode)#3 (5) {
//         ["data"]=>
//         string(1) "D"
//         ["lTag"]=>
//         int(1)
//         ["rTag"]=>
//         int(1)
//         ["lChild"]=>
//         NULL
//         ["rChild"]=>
//         *RECURSION*
//       }
//       ……

关于算法的具体步骤在注释中已经写得很详细了。一句话总结就是在中序遍历的过程中，根据结点的信息来确定它的左右孩子的形式，如果有左右孩子就继续，如果没有任一一个孩子的话，就将左右结点指向前驱或者后继。建立之后的线索二叉树就如图所示：

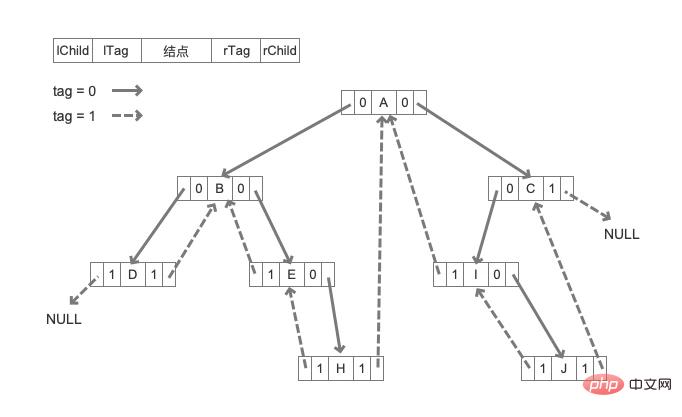
最后就是遍历了。我们需要的是能够快速地获得最左叶子结点的信息，然后就是下一跳的信息，这时，线索的威力就发挥出来了。

// 以 $p 为根的中序线索二叉树中，中序序列下的第一个结点，也就是最左边那个结点
function First(?TBTNode $p){
    while($p->lTag == 0){
        $p = $p->lChild; // 最左下结点（不一定是叶子结点）
    }
    return $p;
}

// 在中序二叉树中，结点 $p 在中序下的后继结点
function NextNode(?TBTNode $p){
    if($p->rTag == 0){
        return First($p->rChild);
    }else{
        return $p->rChild; // 如果 rTag == 1 ，直接返回后继线索
    }
}

// 在中序线索二叉树上进行中序遍历
function Inorder(TBTNode $root){
    //     第一个结点      结点不为空    下一个结点
    for($p = First($root);$p;$p=NextNode($p)){
        echo $p->data, ',';
    }
}

Inorder($tree); // D,B,E,H,A,I,J,C,

当遇到 $lTag 不为 0 的结点时，这个结点就是最左的那个结点了，如果这个不为空的话，【输出】它。接着我们获得下一跳的结点，也就是判断这个结点的右孩子 $rTag 标志，如果是为 0 的，也就是它还有右孩子，【输出】后向下查找，直到找到一个 $rTag 也为 1 的结点，直接返回这个结点的后继，也就是中序遍历的中间那个结点，【输出】它。

最后输出的顺序是不是和我们中序遍历的结果一样呢？注意看代码，在遍历中序线索二叉树的时候，我们没有用一个递归吧，全部是使用的 while() 和 for() 就完成了对这个线索二叉树的遍历。

总结

坚持到现在不容易，不能再小看数据结构了吧？现在还只是树，我们的图都还没开始呢！当然，也不要害怕，一步一步的学，慢慢掌握，不要幻想一口气吃成个胖子。写完这篇文章我也不可能马上就手写出一个中序的线索二叉树来的。大家还是以理解原理为主，如果说真能手写的话，那也是为了面试而去背的或者是为了考研而准备的。这样的小同学在面试中我反而要更多问一些其它的问题，毕竟临时抱佛脚的准备远不如深入理解带来的感悟更能打动人！

测试代码：

https://github.com/zhangyue0503/Data-structure-and-algorithm/blob/master/4.树/source/4.3完全二叉树、线索二叉树及树的顺序存储结构.php

推荐学习：php视频教程

以上が完全二分木と手がかり付き二分木とは何ですか?シーケンシャルストレージ構造はどのようなものですか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。