phpの画像は何ですか？どのように保管できますか?

学習が深まるにつれて、私たちの知識は常に拡大し、豊かになっていきます。ツリー構造にみんな混乱しましたか?信じてください、この図を学習すると、二分木が言葉では言い表せないほど単純であると感じるでしょう。実際、私たちが話しているツリーも特殊な形式のグラフです。

絵の概念

木の学習に関する最初の記事で見た木の絵をまだ覚えていますか?

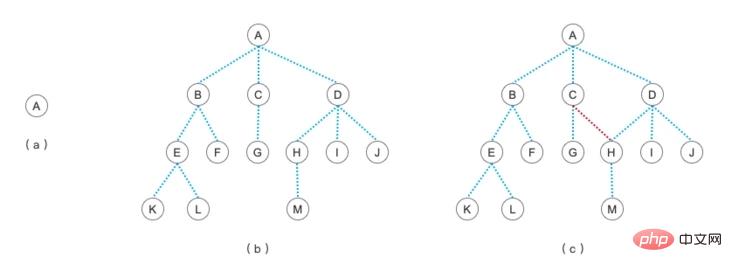
そのとき、私たちは絵cは木ではなく絵だと言いました。なぜ？ツリーの定義から、ツリーはルート ノードを 1 つだけ持つことができ、レベル間に接続はなく、複数の子ノードを持つことができることがわかります。グラフはこれらのルールに従う必要はなく、ノード同士を接続できるのがグラフの特徴です。たとえば、以下の写真はすべて写真です。

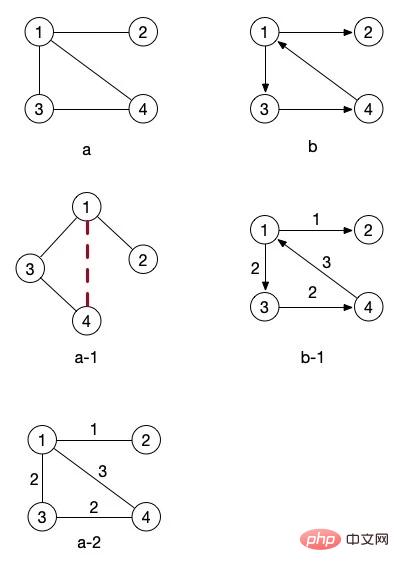
上の図では、図bには矢印があり、図aの接続線には矢印がありませんが、このように方向が明確になっているグラフをいいます。有向グラフ。矢印のないグラフ、つまり方向のないグラフを無向グラフと呼びます。

まず、図 a-1 に注目してみましょう。実際には、図 a が回転しているだけです。みんなも見えるかな？ノード 4 と 1 の間の接続を無視すると、それはツリーになります。それは上記の樹状図の図 c の概念と一致していますか?

グラフのより正式な公式定義は次のとおりです:

グラフ (グラフ) G は 2 つのセット V と E で構成され、G=(V, E) として記録されます。V は頂点です。 E の有限の空でない集合は、V の頂点の有限集合です。これらの頂点のペアもエッジと呼ばれます。

有向グラフでは、開始ノードから指示ノードまでの 2 点を結ぶ線分を として記録できます。 と は 2 つの異なる辺であり、円弧とも呼ばれます。図 a によると、 、 、 、 、 、 、 、 これらのエッジ。図 b では、有向グラフであるため、エッジは 4 つだけです: 、、、。

上の図を見るとよくわかるのに、この定義を見ると混乱しませんか?あなたがテストを受ける必要がある学生であれば、この定義を覚えておく必要があります。私のように学習、応用、理解だけに集中したい場合は、丸暗記する必要はありません。 V はノード、E はこれらのノード間の関係、2 つの頂点間の関係、つまりグラフ上のノードを接続する線分がエッジです。

OK、これら 3 つの最も基本的な概念が理解できたので、引き続き画像に関連する他の用語を学習しましょう。

グラフに関する用語

まず、nはグラフの頂点の数を表し、eは辺の数を表すので、この2つのコードを覚えておいてください。

• (1) サブグラフ: V と E' に V' が含まれる場合、G=(V, E) と G'=(V', E') の 2 つのグラフがあるとします。 E に含まれる場合、G' は G の部分グラフと呼ばれます

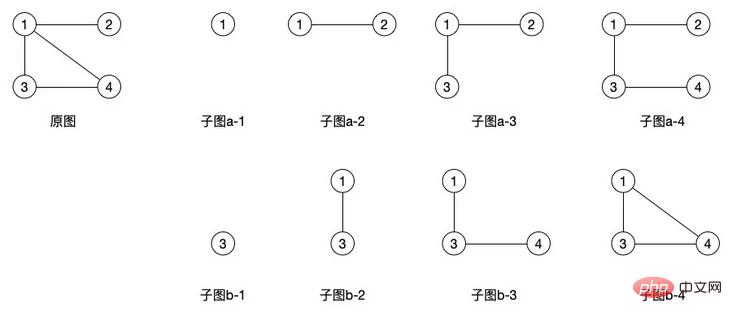
上の図の右側の部分グラフはすべて元の図の部分グラフです。サブグラフは多くの形状を生成でき、有向グラフも同じ概念を持っていることがわかります。ただし、無向グラフと比較すると、有向グラフはエッジに方向性があるため、生成できるサブグラフの数が少なくなります。

• (2) 無向完全グラフと有向完全グラフ: 無向グラフの場合、n(n-1)/2 のエッジがある場合、それは無向完全グラフです。有向グラフの場合、n(n-1) 個の孤立子がある場合、それは有向完全グラフと呼ばれます。 (完全なバイナリ ツリーを参照してください)

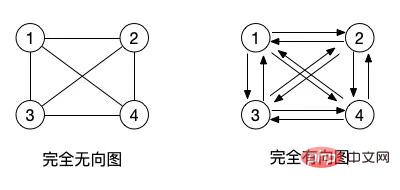
実際、完全なグラフの概念は、グラフ内のすべての隣接するノードにエッジがあるということです。それらをつなぎ合わせます。

有向グラフの場合、エッジには方向性がありますが、もちろん、有向グラフで や などの前後方向を定義することもできます。 1 から 2、または 2 から 1 に進むことができることを示すために、反対方向に 2 つの矢印を描く必要があります。無向グラフでは、これら 2 つのエッジの概念を 1 つのエッジで置き換えます。矢印の方向のないエッジは双方向です。

• (3) スパース グラフとデンス グラフ: エッジや孤立したグラフ (e

• (4) Quanhe Net: 実際のアプリケーションでは、地図上の距離と同じように、各エッジまたは島に何らかの意味を持つ値をマークできます。これらの値はと呼ばれます。重み。権威のある写真をネットワークと呼ぶことができます

上の写真の図 a-2 と図 b-1 の横にある数字は重量を表します。この 2 つの画像はネットワーク画像と呼ばれます。重みの概念については、後で関連するアルゴリズムについて説明するときに学習します。これら 2 つの図から、ノード 1 からノード 4 に移動したい場合、直接 に移動しないことが実際にはっきりとわかります。側にありますが、 、 ルートを選択した方が早いです。

• (5) 隣接点: エッジを持つ 2 つのノードは隣接点です。

• (6) 次数、入次数および出次数:頂点 v の次数は、v に関連付けられたエッジの数を指します。有向グラフの場合、他のノードを指す矢印は出力次数であり、それ自体を指す矢印は次数です

引き続き図 b を見てみましょう。ノード 1 には 2 つの出力次数と 1 つの入力次数があります。これについてはあまり説明の必要はないようです。

• (7) パスとパスの長さ: ある頂点から別の頂点に通過するすべての頂点はパスです。有向グラフの場合、そのパスは矢印の方向になります。パスの長さは、パス上を通過するエッジまたは孤立の数です。

• (8) ループまたはループ: 最初の頂点と最後の頂点が同じパスは、ループまたはループと呼ばれます。ループ

• (9) 接続性、接続されたグラフおよび接続されたコンポーネント: 2 つのノード間にパスがある場合、それらは接続されていると言われます。グラフ全体のすべてのノードが相互に接続できる場合、そのグラフは接続されたグラフです。連結成分は、無向グラフ内の最大連結部分グラフです。

#この図には、次の 3 つの概念も示されています。無向グラフでは、連結成分は最大連結部分グラフと等しくなります。このグラフには 2 つの連結成分があります。

• (10) 最大接続サブグラフ: 接続サブグラフに含めることができるノードの最大数。ノードを 1 つ追加すると、サブグラフは接続グラフではなくなります。

##(11) スパニング ツリー: グラフ内のすべての頂点を含む最小の接続されたサブグラフですが、ツリーを形成するのに十分な n-1 個のエッジだけが含まれます。このような接続されたサブグラフはスパニング ツリーです。接続されたグラフの
# は、実際にはグラフ内のすべてのノードを接続するパスです。連結成分のグラフでは、2 つの連結成分に基づいて 2 つの最小スパニング ツリーを生成します。接続コンポーネント 1 のスパニング ツリーのノードは必ずしもこの構造である必要はなく、この最小スパニング ツリーを生成するためのトラバース方法に応じて、ノード 4 をノード 2 の下に置くことができます。

上の図 a の最小スパニング ツリーは、実際には赤い点線のない図 a-1 になります。もちろん、ノード 4 をノード 1 の下に配置することもできます。また、プログラムがグラフをどのように走査してどのような種類のツリーを生成するかによっても異なります。

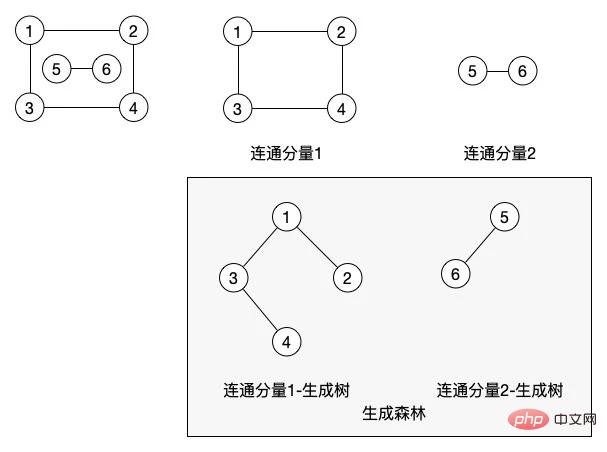
(12) スパニング フォレスト: 非接続グラフでは、接続された各コンポーネントが接続されたスパニング ツリーを生成し、非接続グラフ全体のスパニング フォレストを形成できます。

これを読んだ後、めまいがしませんか?問題ではありません。これらの用語は今後の研究で頻繁に使用されますが、これは最も包括的なものではありません。参考文献やその他の学習教材を使用して、グラフ関連の用語をより深く学習し、理解することができます。

まとめ

グラフの概念はほぼ紹介されているので、それを理解して次の内容を学習し続けることができます。これはほんの始まりにすぎませんが、多くの学生は、ツリー構造に比べて大幅に改善されたと感じるでしょう。グラフに関する内容がまだ理解できていなくても、以下の知識を学べばツリー構造への理解が確実に深まるのでご安心ください。なぜ？ツリーは実際にはループのないグラフであり、深さまたは幅によってたどることができますが、グラフはより複雑です。さて、未来にはまだ希望があると思いますか？学習は段階的なプロセスであることが多く、現在の知識と過去の知識の間には常につながりがあります。最初はあまり考えすぎず、ステップバイステップで進めてください。

おすすめ:

《2021年PHP面接質問まとめ（集）》《phpビデオチュートリアル》

以上がphpの画像は何ですか？どのように保管できますか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。