1 つの変数で解決とは何ですか? Excel の単一変数ソリューション ケース分析
財務担当者として、昇進して給与を上げたい場合は、統計を収集するだけでなく、会社のニーズに基づいてデータを予測する必要もあります。手動で行う場合は、非常に複雑な数学的演算を行う必要がありますが、実際、Excel にはデータ予測を簡単に完了できるツールが用意されており、それが Excel の単一変数解決関数です。

現在、分析と予測は財務担当者の仕事の重要な部分になってきています。最も一般的で効果的なのは単変量解析です。単変量解析を完了するには、内挿法、試行錯誤法など、さまざまな方法があります。しかし、Excel の専門家にとって、単一変数のソリューションが最良の答えであることは間違いありません。
1. 単一変数解とは何ですか?
下の図に示すように、セル B2 は定数であり、セル B4 は B2 に対する特定の演算の結果です。 B2 の値を変更すると、B4 も変更されます。ここでは、B2 を変数セル、B4 をターゲット セルと呼びます。
単一変数の解は関数式の逆演算です。
それでは、Excel の単一変数解はどこにあるのか、また Excel における単一変数解の原理と Excel の単一変数解のケースについて、この記事で説明します。 例として、目標値を250とします。具体的な操作は以下のとおりです。ステップ01 Excelの[データ]タブ-[シミュレーション]をクリックします。 [分析] - [単一 [単一変数解]ボタンをクリックすると、[単一変数解]ダイアログ ボックスが表示されます。
ステップ 02 ダイアログ ボックスで、ターゲット セルを $B$4 に設定し、ターゲット セルのターゲット値を 250 に手動で入力します。変数セルを $B$2 に設定します。以下に示すように。
2。これは、ターゲット セル値の範囲に含まれている必要があります。つまり、ターゲット セル値をターゲット値と等しくする変数セル値が存在します。そうでない場合、単一変数ソリューションの実行時間が長くなり、最終的には、条件を満たすソリューションを求めるプロンプトが表示されます。条件が得られない。
ステップ 03
[OK] ボタンをクリックして、単一変数の解決を実行します。 Excel は自動的に反復演算を実行し、最終的に対象セル (B4) が対象値 (250) と等しい場合に変数セルの値 (120) を取得し、変数セル (B2) に自動的に代入します。以下に示すように、「OK」をクリックします。
#2. Excel 単一変数ソリューションの例
Excel 単一変数ソリューションケース 1 ローン金利の問題
従業員 A は会社 A の融資専門家です。会社は銀行から 5 年間の 3,500 万のローンを申請し、元金と返済を計画しています。利息は毎月均等に分割して支払われます。銀行の当初の年利計画である 6.3% に基づいて、従業員 A は、会社 A が月々 681,500 円を支払う必要があると計算しました。次の図に示すように、=PMI (年利/12、期間数、借入金額) の計算式を使用すると、月々の返済利息 681,500 を計算できます。
しかし、計算してみると、企業が融資を受けた後に返済できる資金は月あたり 675,000 円しかありません。財務責任者は、銀行と交渉するために、会社が許容できる最大年利を計算するように従業員 A に依頼しました。
ある社員が、年利のセルB5が変数セル、月々の元利返済額のB6が対象セルで、目標値が67.5であると分析しました。これはまさに単一変数ではないでしょうか。解決?

#Step 02 反復演算後、条件を満たす解がすぐに表示されるので、[OK]をクリックすると単一変数解が完成します。次のように。
上のグラフから、会社が受け入れることができる最大年利は 5.9% であることがわかります。これは単一変数のソリューションであり、効率的であるだけでなく、正確でもあります。
#Excel の単一変数解のケース 2 等価金利問題
B 従業員は、ある企業の投資です。某企業マネージャーによると、同社は新規プロジェクトの取得を計画しており、投資額は16億元(累計投資額の現在価値)、予定単価は18,800元、平均支払期間は5年となる見込みだ。計算すると、同社のプロジェクトへの投資に相当する利率は 8.8% となります。 下図に示すように、=RRI(返済期間、投資総額の現在価値、売上収益)という式を使用して、将来に対応する現在の投資価値の実際の等価金利を計算できます。価値。Step 01 設定したデータ関係に従って、[単一変数解]ボタンをクリックし、対象セルを$B$8、対象値を10%に設定し、変数セルを $B$3 に設定し、[OK]をクリックして単一変数解決を実行します。
ステップ 02 反復処理を行うと、条件を満たす解がすぐに表示されますので、[OK] をクリックすると単一変数解が完成します。
上の図に示すように、結果は、最低販売価格が 19,879.09 元に調整され、会社の要件を満たすことができます。Excel 単一変数ソリューション ケース 3 損益分岐点問題
従業員 C は、製造会社の財務マネージャーです。市場の影響 業績不振のため、会社は工場の生産量を 200,000 個に減らす予定です。従業員 C は、この生産量での工場の損益を計算する必要があります。製品の平均販売価格は生産量が増加するにつれて低下し、3 つの手数料は売上と収益に一定の比例関係にあることが知られています。計算すると、生産量20万元の下での総利益は1383万6800元となる。以下に示すように。Step 01 設定したデータ関係に従って、[単一変数解]ボタンをクリックし、対象セルを$B$12、対象値を0、変数セルを$ B$3に設定し、[OK]をクリックすると単一変数解決が実行されます。
ステップ 02 反復演算後、条件を満たす解がすぐに表示されますので、[OK] をクリックすると単一変数解が完成します。
以上が1 つの変数で解決とは何ですか? Excel の単一変数ソリューション ケース分析の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7504
7504
 15
15
 1378
1378
 52
52
 78
78
 11
11
 19
19
 54
54
 Excelで印刷時に枠線が消えてしまった場合はどうすればよいですか?
Mar 21, 2024 am 09:50 AM
Excelで印刷時に枠線が消えてしまった場合はどうすればよいですか?
Mar 21, 2024 am 09:50 AM
印刷が必要なファイルを開いたときに、印刷プレビューで表の枠線が何らかの原因で消えてしまった場合は、早めに対処する必要があります。 file このような質問がある場合は、エディターに参加して次のコースを学習してください: Excel で表を印刷するときに枠線が消えた場合はどうすればよいですか? 1. 次の図に示すように、印刷する必要があるファイルを開きます。 2. 以下の図に示すように、必要なコンテンツ領域をすべて選択します。 3. 以下の図に示すように、マウスを右クリックして「セルの書式設定」オプションを選択します。 4. 以下の図に示すように、ウィンドウの上部にある「境界線」オプションをクリックします。 5. 下図に示すように、左側の線種で細い実線パターンを選択します。 6.「外枠」を選択します
 Excelで3つ以上のキーワードを同時にフィルタリングする方法
Mar 21, 2024 pm 03:16 PM
Excelで3つ以上のキーワードを同時にフィルタリングする方法
Mar 21, 2024 pm 03:16 PM
Excelは日々の事務作業でデータ処理に使用されることが多く、「フィルター」機能を使用することが多いです。 Excel で「フィルタリング」を実行する場合、同じ列に対して最大 2 つの条件しかフィルタリングできません。では、Excel で同時に 3 つ以上のキーワードをフィルタリングする方法をご存知ですか?次に、それをデモンストレーションしてみましょう。 1 つ目の方法は、フィルターに条件を徐々に追加することです。条件を満たす 3 つの詳細を同時にフィルターで除外する場合は、まずそのうちの 1 つを段階的にフィルターで除外する必要があります。最初に、条件に基づいて姓が「Wang」の従業員をフィルタリングできます。 [OK]をクリックし、フィルター結果の[現在の選択をフィルターに追加]にチェックを入れます。手順は以下の通りです。同様に再度個別にフィルタリングを行う
 Excelテーブル互換モードを通常モードに変更する方法
Mar 20, 2024 pm 08:01 PM
Excelテーブル互換モードを通常モードに変更する方法
Mar 20, 2024 pm 08:01 PM
私たちは日々の仕事や勉強で、他人からExcelファイルをコピーし、そのファイルを開いて内容を追加したり、再編集したりして保存することがありますが、互換性チェックのダイアログボックスが表示されることがあり、非常に面倒です。ソフトウェア. 、通常モードに変更できますか?そこで以下では、エディターがこの問題を解決するための詳細な手順を紹介します。一緒に学びましょう。最後に、忘れずに保存してください。 1. 図に示すように、ワークシートを開き、ワークシートの名前に追加の互換モードを表示します。 2. このワークシートでは、内容を変更して保存すると、図のように互換性チェックのダイアログが必ず表示され、非常に面倒です。 3. [Office] ボタンをクリックし、[名前を付けて保存] をクリックして、
 Excelで下付き文字を入力する方法
Mar 20, 2024 am 11:31 AM
Excelで下付き文字を入力する方法
Mar 20, 2024 am 11:31 AM
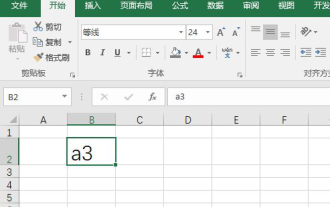
e私たちはExcelを使ってデータテーブルなどを作成することがあります。パラメータ値を入力するときに、特定の数値の上付きまたは下付きが必要になることがあります。たとえば、数式がよく使用されます。では、Excelで下付き文字を入力するにはどうすればよいですか?詳細な手順を見てください: 1. 上付き文字の方法: 1. まず、Excel に a3 (3 は上付き文字) と入力します。 2. 数字「3」を選択し、右クリックして「セルの書式設定」を選択します。 3. 「上付き文字」をクリックし、「OK」をクリックします。 4. ほら、効果はこんな感じです。 2. 下付き文字の設定方法: 1. 上付き文字の設定方法と同様に、セルに「ln310」(3 は下付き文字) と入力し、数字の「3」を選択し、右クリックして「セルの書式設定」を選択します。 2.「下付き文字」にチェックを入れて「OK」をクリックします。
 Excelで上付き文字を設定する方法
Mar 20, 2024 pm 04:30 PM
Excelで上付き文字を設定する方法
Mar 20, 2024 pm 04:30 PM
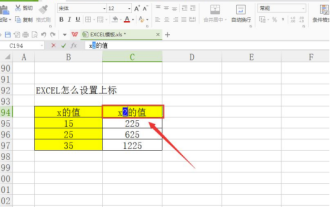
データを処理していると、倍数や温度などのさまざまな記号が含まれるデータに遭遇することがあります。 Excel で上付き文字を設定する方法をご存知ですか? Excel を使用してデータを処理する場合、上付き文字を設定しないと、大量のデータを入力するのがさらに面倒になります。今回はエクセルの上付き文字の具体的な設定方法をエディターがお届けします。 1. まず、図に示すように、デスクトップで Microsoft Office Excel ドキュメントを開き、上付き文字に変更する必要があるテキストを選択します。 2. 次に、図に示すように、右クリックして、クリック後に表示されるメニューで「セルの書式設定」オプションを選択します。 3. 次に、自動的に表示される「セルの書式設定」ダイアログボックスで
 エクセルでiif関数を使う方法
Mar 20, 2024 pm 06:10 PM
エクセルでiif関数を使う方法
Mar 20, 2024 pm 06:10 PM
ほとんどのユーザーは Excel を使用してテーブル データを処理します。実は Excel にも VBA プログラムがあります。専門家を除けば、この関数を使用したユーザーはあまり多くありません。VBA で記述するときによく使用されるのが iif 関数です。実際には、次の場合と同じです。関数の機能は似ていますが、iif関数の使い方を紹介します。 SQL ステートメントには iif 関数があり、Excel には VBA コードがあります。 iif 関数は Excel ワークシートの IF 関数と似ており、論理的に計算された真値と偽値に基づいて真偽値を判定し、異なる結果を返します。 IF 関数の使用法は (条件、はい、いいえ) です。 VBAのIF文とIIF関数、前者のIF文は条件に応じて異なる文を実行できる制御文であり、後者は条件に応じて異なる文を実行できる制御文です。
 Excelの読み取りモードを設定する場所
Mar 21, 2024 am 08:40 AM
Excelの読み取りモードを設定する場所
Mar 21, 2024 am 08:40 AM
ソフトウェアの学習では、Excel が便利なだけでなく、実際の作業で必要なさまざまな形式に対応できるため、Excel の使用に慣れています。Excel は非常に柔軟に使用でき、今日は「みんなのために:Excelの読み取りモードを設定する場所」を持ってきました。 1. コンピュータの電源を入れ、Excel アプリケーションを開き、目的のデータを見つけます。 2. Excel で読み取りモードを設定するには 2 つの方法があります。 1 つ目: Excel には、Excel レイアウトで多数の便利な処理メソッドが配布されています。 Excelの右下に読み取りモードを設定するショートカットがあります。バツマークのパターンを見つけてクリックすると、読み取りモードに入ります。バツマークの右側に小さな立体マークがあります。 。
 ExcelアイコンをPPTスライドに挿入する方法
Mar 26, 2024 pm 05:40 PM
ExcelアイコンをPPTスライドに挿入する方法
Mar 26, 2024 pm 05:40 PM
1. PPT を開き、Excel アイコンを挿入する必要があるページに移動します。 「挿入」タブをクリックします。 2. [オブジェクト]をクリックします。 3. 次のダイアログボックスが表示されます。 4. [ファイルから作成]をクリックし、[参照]をクリックします。 5. 挿入する Excel テーブルを選択します。 6. [OK] をクリックすると、次のページが表示されます。 7. [アイコンで表示]にチェックを入れます。 8. 「OK」をクリックします。
















