JavaScriptで素数を見つける方法

素数の求め方: 1. 1~n の範囲のすべての自然数をたどり、n で割ります。余りが 0 の場合は、n が素数ではないことを意味します。それ以外の場合は、n が素数であることを意味します。素数。構文「for(i=2 ;i

このチュートリアルの動作環境: Windows7 システム、JavaScript バージョン 1.8.5、Dell G3 コンピューター。

素数の概念

素数は素数とも呼ばれ、1 とそれ自体を除く他の自然数で割り切れない数を指します。 1 より大きい自然数のうち。

100 以内の素数: 2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71 、73、79、83、89、97、合計25。

JavaScript を使用して素数を決定する 4 つの方法

1. 素数は 1 とそれ自体でのみ割り切れます

素数は 1 とそれ自身で割り切れるだけなので、開区間 (1, n) 内のすべての自然数をたどって n で割ります。整数の割り算がある場合、つまり余りが 0 である場合、それは次のことを意味します。数値 n は素数ではありません。それ以外の場合は素数です。

function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>しかし、このアルゴリズムの複雑さは O(n)</p><h3 id="strong-です-素数の平方根の範囲-strong"><strong>2 です。素数の平方根の範囲</strong></h3><p>n がそうでないと仮定すると、素数の場合は、n を除きます。1 と n だけでなく、i と j でも割り算できます。つまり、n / i = j...0、たとえば、15 は素数ではありません、15 / 3 = 5、たとえば、35 は素数ではありません、35 / 5 = 7、これは i と j がそれぞれ (1, Math.sqrt(n)] と [Math.sqrt(n), n) になければなりません。たとえば、Math.sqrt(15) ≈ 3.8 の場合、3 は (1, 3.8] に入り、5 は [3.8, 15) になります。たとえば、Math.sqrt(4) = 2 の場合、2 は (1,2) にあり、[2,4) にもあります。 </p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 2; i <p>このときのアルゴリズムの複雑さは O(sqrt(n))</p><h3 id="%E7%B4%A0%E6%95%B0%E4%B8%8D%E8%83%BD%E6%98%AF%E9%99%A4%E4%BA%862%E5%A4%96%E7%9A%84%E5%81%B6%E6%95%B0">
<strong>3 です。素数は 2</strong># 以外の偶数にすることはできません。 </h3>##2 を除き、すべての偶数は素数ではありません<p></p><p>##</p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  if (n % 2 === 0) {
    return false;
  }
 
  for (let i = 3; i <img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/image/644/149/762/1663645614907138.png" class="lazy" title="1663645614907138.png" alt="JavaScriptで素数を見つける方法">n は、上の図の水色の部分のみになります。 <p> したがって、上記のアルゴリズムはループを半分に削減し、時間計算量は O(sqrt(n) / 2) になります。 </p><p>このアルゴリズムのコードは n にすることができないことに注意してください。 % 2 == = 0 の判定条件をループに追加します。以下のコードには抜け穴があります。</p><pre class="brush:php;toolbar:false">function isPrime(n) {
  n = parseInt(n);
 
  if (n  1;
  }
 
  for (let i = 3; i <p>このとき、4、6、8 はすべて素数と判定されてしまいます。 </p><p>この脆弱性の原因は、for ループのループ条件 i </p><p>このアルゴリズムは、ループ条件 i = i^2 = 9 のときのみ、n の値が正しいことを保証できます。 </p><p></p>4. 5 以上の素数は 6 の倍数に隣接する必要があります<h3 id="%E5%A4%A7%E4%BA%8E%E7%AD%89%E4%BA%8E5%E7%9A%84%E7%B4%A0%E6%95%B0%E4%B8%80%E5%AE%9A%E5%92%8C6%E7%9A%84%E5%80%8D%E6%95%B0%E7%9B%B8%E9%82%BB">
<strong></strong>5 以上の素数は 6 の倍数に隣接する必要があります</h3><p> (この文は、「</p> に隣接する数値および 6 の倍数は 5 より大きい素数 <p> でなければならない」と同等ではないことに注意してください。この結論は真実ではありません。) <span style="text-decoration:line-through;"></span> </p><p><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/image/346/360/896/166364562667908JavaScriptで素数を見つける方法" class="lazy" title="166364562667908JavaScriptで素数を見つける方法" alt="JavaScriptで素数を見つける方法">上の図に示すように、5 以上の数値は 6y-1、6y、6y 1、6y 2、6y 3、6y 4 (y>=1) に分割されます。 </p><p>このうち、6y、6y 2 、6y 3 、6y 4 は素数になることができず、6y-1 と 6y 1</p><p><strong><span   style="max-width:90%"> だけが素数になる可能性があります。 </span></strong>さらに、6y-1 (y>=1) と 6y 5 (y>=0) は同等です。 </p><p>したがって、n が 6y-1 (または 6y 5) および 6y 1 ではない数値を直接除外できます。消去方法は、</p><pre class='brush:php;toolbar:false;'>  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }

です。次に、6y- を消去する必要があります。 1 (または 6y 5 の非素数) と 6y 1、

  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }

ここで混乱している点が 2 つあるかもしれません:

i の増分はなぜですかfor ループ

6
• for ループの素数決定条件がなぜ n % i === 0 || n %
(i 2)
• = == 0

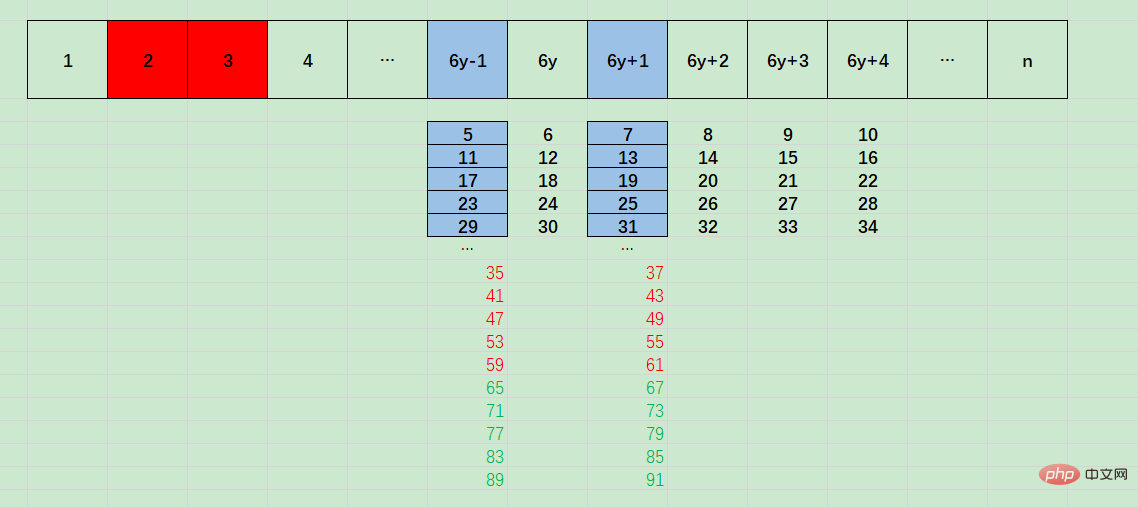上の図を見ると、6y-1 は底が 5、差が 6 の等差数列であることがわかります。つまり、5 6x:

• 对于 5 + 6x 而言，如果x为5的倍数（5 * z），则5 + 6x = 5 + 6 * 5 * z = 5 *（1+6z）,则此时5 + 6x可以被5整除。
• 5 + 6x 还可以转化为 5 + 6 + 6 * (x-1) = 11 + 6(x-1)，则只要x-1为11的倍数，则5 + 6x可以被11整除，
• 5 + 6x 还可以转化为 5 + 12 + 6 * (x-2) = 17 + 6(x-2)，则只要x-2为17的倍数，则5 + 6x可以被17整除
• ......

6y+1，是基数为7，差值为6的等差数列，即 7 + 6x :

• 对于 7 + 6x 而言，如果x为7的倍数（7 * z），则7 + 6x = 7 + 6 * 7 * z = 7 *（1+6z）,则此时7 + 6x可以被7整除。
• 7 + 6x 还可以转化为 7 + 6 + 6 * (x-1) = 13 + 6(x-1)，则只要x-1为13的倍数，则7 + 6x可以被13整除，
• 7 + 6x 还可以转化为 7 + 12 + 6 * (x-2) = 19 + 6(x-2)，则只要x-2为19的倍数，则7 + 6x可以被19整除，
• ......

所以6y-1和6y+1可能整除的数自增量为6，这是for循环i自增为啥是 6的原因

且6y-1和6y+1的整除数基数为5和7，相差为2，这是for循环中素数判定的条件为啥是 n % i === 0 || n % (i+2) === 0的原因

function isPrime(n) {
  n = parseInt(n);
 
  if (n <= 3) {
    return n > 1;
  }
 
  if (n % 6 !== 1 && n % 6 !== 5) {
    return false;
  }
 
  for (let i = 5; i <= Math.sqrt(n); i += 6) {
    if (n % i === 0 || n % (i + 2) === 0) {
      return false;
    }
  }
 
  return true;
}

此时时间复杂度为 O（sqrt(n) / 3） 

【相关推荐：javascript视频教程、编程基础视频】

以上がJavaScriptで素数を見つける方法の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。