Java データ構造の一般的な並べ替えアルゴリズム (概要共有)

この記事では、Java に関する関連知識を提供します。主に、直接挿入ソート、ヒル ソート (減分ソート)、選択ソート、ヒープ ソートなどの一般的なソート アルゴリズムを紹介します。見てみましょう。皆様のお役に立てれば幸いです。

#1. 順序を理解する

学校では、運動会や軍事訓練に参加したい場合、たとえば、授業で教師が持つ出席簿は、通常、生徒番号の低い人から高い人の順に並べられます。もう 1 つの例は、プログラミング言語のランキングです。これも並べ替えられています。

#人生には、並べ替えのシナリオが非常にたくさんあります。並べ替えが依然として非常に重要であることがわかります。この章では、一般的な並べ替えアルゴリズムをいくつか紹介します。

いわゆる並べ替えとは、上の例で言えば、1 つまたはいくつかのキーワードのサイズに応じて増加または減少するように配置する操作です。これは並べ替えであり、

並べ替えの安定性##も必要です#、例:

たとえば、データのセット: B D A C A F があります。これは、ascll コードに従ってソートする必要があります。A は 2 つあり、最初に表示される A と呼びます。 A1、そして 2 番目に現れる A2。

並べ替え後の結果が

A1 A2 B C D F であると仮定すると、この並べ替えアルゴリズムは安定しています。

ソート後の結果が

A2 A1 B C D F であると仮定すると、このソート アルゴリズムは不安定です。

つまり、並べ替え対象のデータ内に同じ要素が 2 つある場合、並べ替えが完了した後も 2 つの要素間の関係は変わりません。たとえば、A1 は A2 の前にあります。ソート後も、A1 はまだ A2 の前にあります。これは安定したソート アルゴリズムです。

注:

不安定な並べ替えアルゴリズムは本質的に不安定ですが、安定した並べ替えアルゴリズムは不安定になるように設計される可能性があります。 2. 一般的なソートの分類

#この図は、後で説明するソート アルゴリズムをまとめたもので、正式にこの章の学習に入ります。 (ソートアルゴリズムの章では、デフォルトは 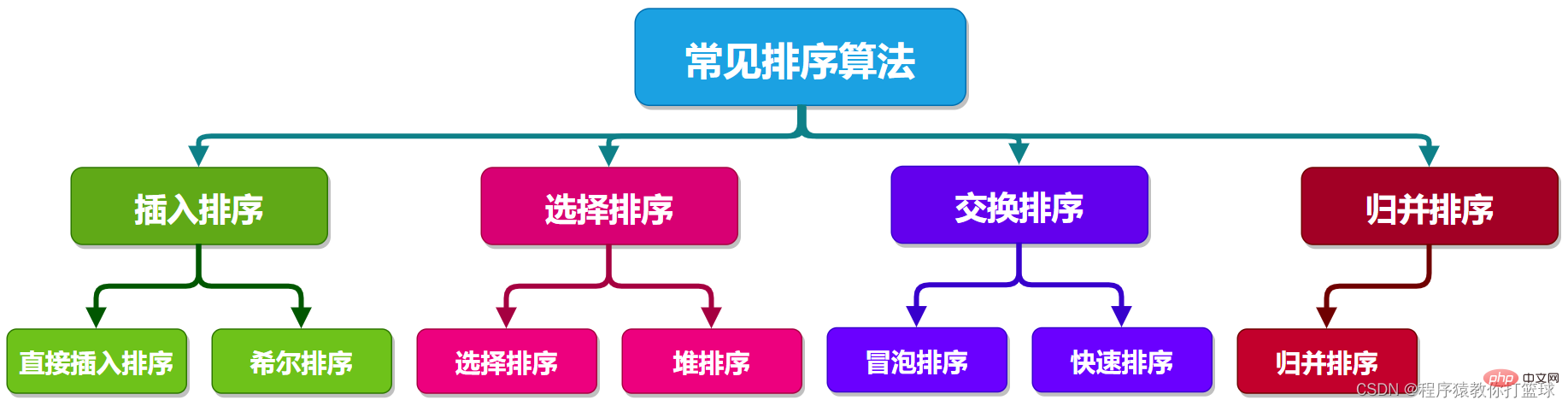Ascending order

です)

注: 後述する複雑さのログは 2 に基づいており、特別なものにはマークが付けられます。 3. 直接挿入ソート

さて、すべての友達に、トランプに触れているところを想像してもらいたいのですが、彼らは最初のカードに触れ、それを手に置きました。その後、カードを1枚引き、このカードとあなたの手札とを比べて適切な位置に置き、さらにもう1枚カードを引き、このカードとあなたの手札2枚を比べて適切な位置に置きます。

これは直接挿入ソートです。簡単に言うと、毎回取得する要素が順序付けられたシーケンスに挿入されます。つまり、各カードが引かれる前に、手札のカードがソートされます。はい、新しく引いたカードと、手札にある注文したカードを比較し、適切な位置に置くだけです。

ここでは、静的な画像を使って簡単に説明します:

一般的な概念はすでに理解しました。次に、コードを使用する必要があります。それを実装するには: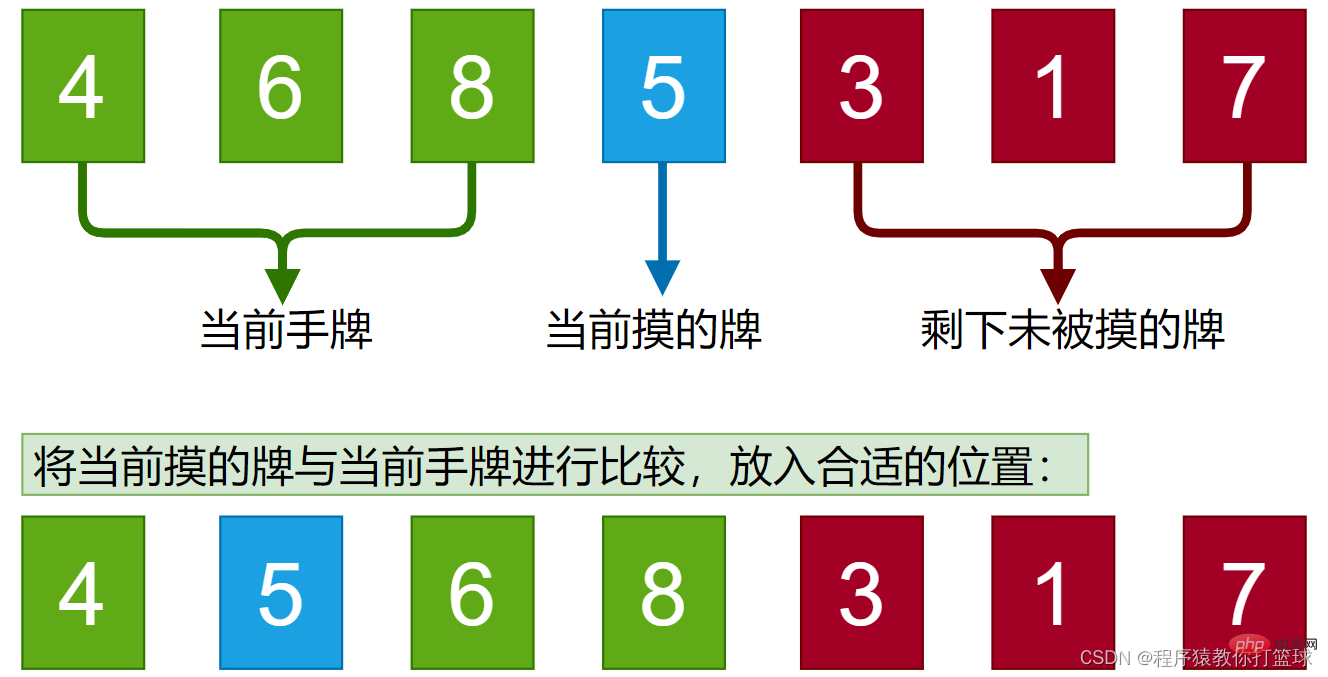

public void insertSort(int[] array) {
    // 外循环控制趟数, 第一张牌默认有序, 所以 i 从 1 开始
    for (int i = 1; i < array.length; i++) {
        int tmp = array[i]; //当前摸到的牌
        // 每次从手中牌的最后一张牌开始比较, 一直比到第一张牌
        int j = i - 1;
        for (; j >= 0; j--) {
            //如果当前位置的牌,大于我摸到的牌,就往后挪
            if (array[j] > tmp) {
                array[j + 1] = array[j];
            } else {
                break;
            }
        }
        // 把摸到的牌放到对应位置上
        array[j + 1] = tmp;
    }
}

時間計算量分析:

外側のループは合計で n - 1 回かかり、内側のループは毎回最悪のケースになります。 次に、 1...n 回比較し、n より前の小さい項を削除する必要があります。つまり (n - 1) * n 回、つまり n^2 - n を削除し、最小項と最後の ## を削除します。 # 時間計算量は O(n^2)
• 空間計算量分析:tmp 変数 i、j、定数を開くだけです。つまり、空間計算量: O(1 )
• 安定性: 安定性
• データが順序付けられた状況に近づくほど、時間効率が高くなります。
• 4. ヒル ソート (増分ソートの削減)

このソートは、直接挿入ソートを最適化したものです。あなたの目の前です。わかりました。ナンバー プレートが 8 枚ありますが、順番が違います。ナンバー プレートをグループ化する必要があります。要件に従って、最初の間隔は 4 つのナンバー プレートをグループにします。グループが分割された後、直接挿入します。 2回目 2回目はナンバープレート2枚のグループで直接挿入ソートを行う 3回目はナンバープレート1枚のグループ、3回目はナンバープレートのグループで直接挿入ソートを行う直接挿入ソートが行われます。

これは少し理解できませんが、問題はありません。上で言ったことをもう一度理解するために絵を描いてみましょう:

由上图我们可以发现，当间隔 > 1 的时候，都是预排序，也就是让我们的数据更接近有序，但是当间隔为 1 的时候，就是直接插入排序了，前面我们说过，直接插入排序，再数据接近有序的时候时间效率是很快的。由此可见，希尔排序，是直接插入排序的优化版。

如何在代码中实现呢？间隔的值如何取呢？代码中把这个间隔的值称为 gap，这个 gap 的取值方法有很多，有的人提出 gap 为奇数好，有的提出 gap 为偶数好，我们就采取一种比较简单的方法来取 gap 值，首次取数组长度一半的值为 gap，后续 gap /= 2，即可。当 gap 为 1，也就是直接插入排序了。

代码实现如下：

public void shellSort(int[] array) {
    // gap初始值设置成数组长度的一半
    int gap = array.length >> 1;
    // gap 为 1 的时候直接插入排序
    while (gap >= 1) {
        shell(array, gap);
        gap >>= 1; // 更新 gap 值 等价于 -> gap /= 2;
    }
}
private void shell(int[] array, int gap) {
    for (int i = gap; i < array.length; i++) {
        int tmp = array[i];
        int j = i - gap;
        for (; j >= 0; j -= gap) {
            if (array[j] > tmp) {
                array[j + gap] = array[j];
            } else {
                break;
            }
        }
        array[j + gap] = tmp;
    }
}

如果实在是不好理解，就结合上边讲的直接插入排序来理解，相信你能理解到的。

• 时间复杂度分析：希尔排序的时间复杂度不好分析， 这里我们就大概记一下，约为 O(n^1.3)，感兴趣的话，可以查阅一下相关书籍。
• 空间复杂度分析：仍然开辟的是常数个变量，空间复杂度为 O(1)
• 稳定性：不稳定

5、选择排序

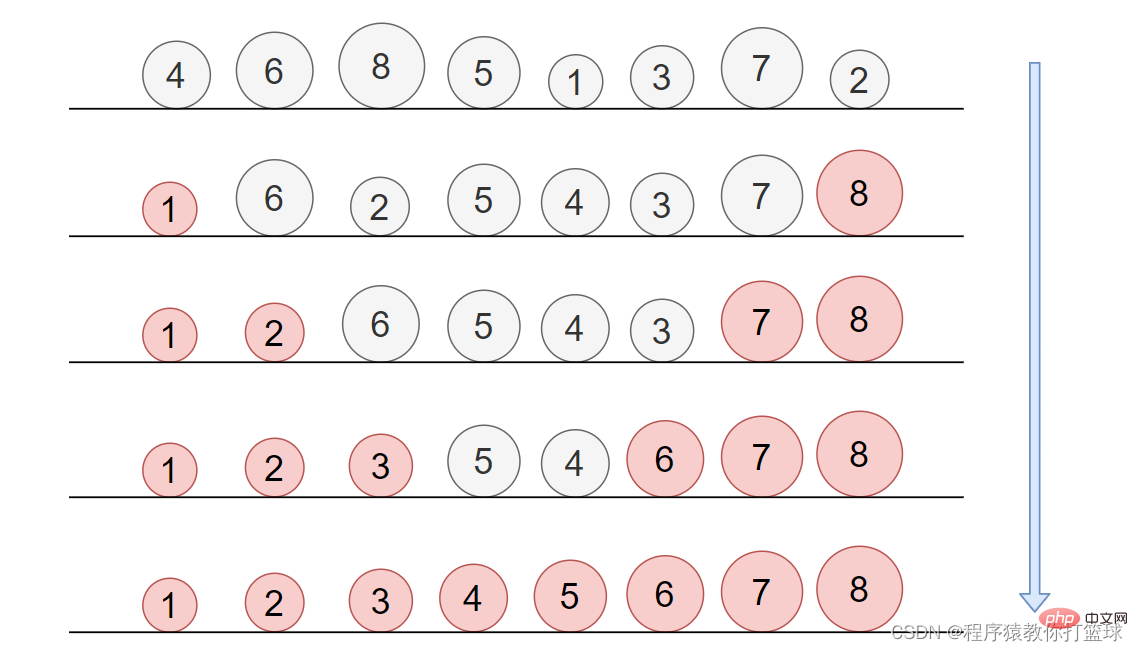
这个排序是个很简单的排序，你想象一下，有个小屁孩，喜欢玩小球，我给他安排了个任务，把这一排小球从小到大排列起来，摆给我看，于是小屁孩就找，每次从一排小球中找出最大的，放到最后，固定不动，那是不是也就是说，每次能确定一个最大的石子的最终位置了。我们来看图：

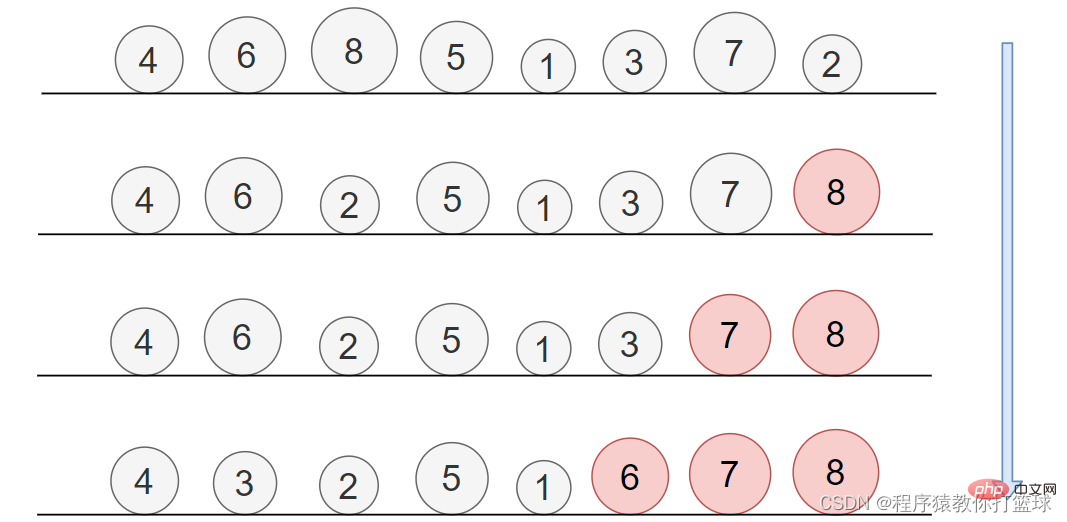
通过图片我们也能看出来，每次找到最大值于最后一个值交换，所以每趟都能把最大的放到最后固定不动，每趟能排序一个元素出来，那这样用代码来实现就很简单了：

public void selectSort(int[] array) {
    int end = array.length - 1;
    // 剩最后一个元素的时候, 不用比较了, 已经有序了
    // 所以 i < array.length - 1
    for (int i = 0; i < array.length - 1; i++) {
        int max = 0;
        int j = 0;
        while (j <= end) {
            if (array[j] > array[max]) {
                max = j;
            }
            j++;
        }
        //找到了最大值的下标, 把最大值与最后一个值交换
        swap(array, max, end--); // end-- 最后一个元素固定了, 不用参与比较
    }
}

这个算法有没有可以优化的空间呢？

有！那么既然小屁孩能一次找出最大的球，那能不能让小屁孩一次找出两个球出来呢？分别是这些球中，最大的和最小的，最大的放在最右边，最小的放在最左边，那么我们每次就能确定两个球的最终位置，也就是我们一次能排序两个元素。图解：

代码实现如下：

public void selectSort(int[] array) {
    int left = 0;
    int right = array.length - 1;
    while (left < right) {
        int maxIndex = left;
        int minIndex = left;
        // i = left + 1 -> 每次找最大最小值下标的时候, 可以不用算默认给的最大值和最小值下标
        for (int i = left + 1; i <= right; i++) {
            if (array[i] > array[maxIndex]) {
                maxIndex = i;
            }
            if (array[i] < array[minIndex]) {
                minIndex = i;
            }
        }
        swap(array, minIndex, left);
        // 如果最大值为 left 的位置情况的话, 走到这, 最大值已经被交换到 min 位置上了
        if (maxIndex == left) {
            // 更新最大值的位置
            maxIndex = minIndex;
        }
        swap(array, maxIndex, right);
        left++;
        right--;
    }
}

• 时间复杂度分析：虽然是优化了，但去小项之后，还是 O(n^2)
• 空间复杂度分析：O(1)
• 稳定性：不稳定
• 实际开发中用的不多

6、堆排序

如果你有学习过优先级队列，或者看过博主优先级队列的文章，那么这个排序对于你来说还是很轻松的，当然在堆排序的讲解中，不会过多的去介绍堆的概念，如果对这部分概念还不理解，可以移至博主的上一篇文章进行学习。

堆排序，简单来说，就是把一组数据，看成一个完全二叉树，再把这棵树，建大堆或者建小堆，接着进行排序的一种思路。至于如何建大堆或小堆，和向上调整算法以及向下调整算法，这里也不多介绍了，博主的上篇文章都详细介绍过。

这里我们来分析一下，排升序应该建什么堆？大堆！排降序建小堆！

这里我们来排升序，建大堆，因为大堆堆顶元素一定是堆中最大的，所以我们可以把堆顶元素和最后一个元素进行交换，这样我们就确认了最大值的位置，接着将交换后的堆顶元素进行向下调整，仍然使得该数组满足大堆的特性！图解如下：

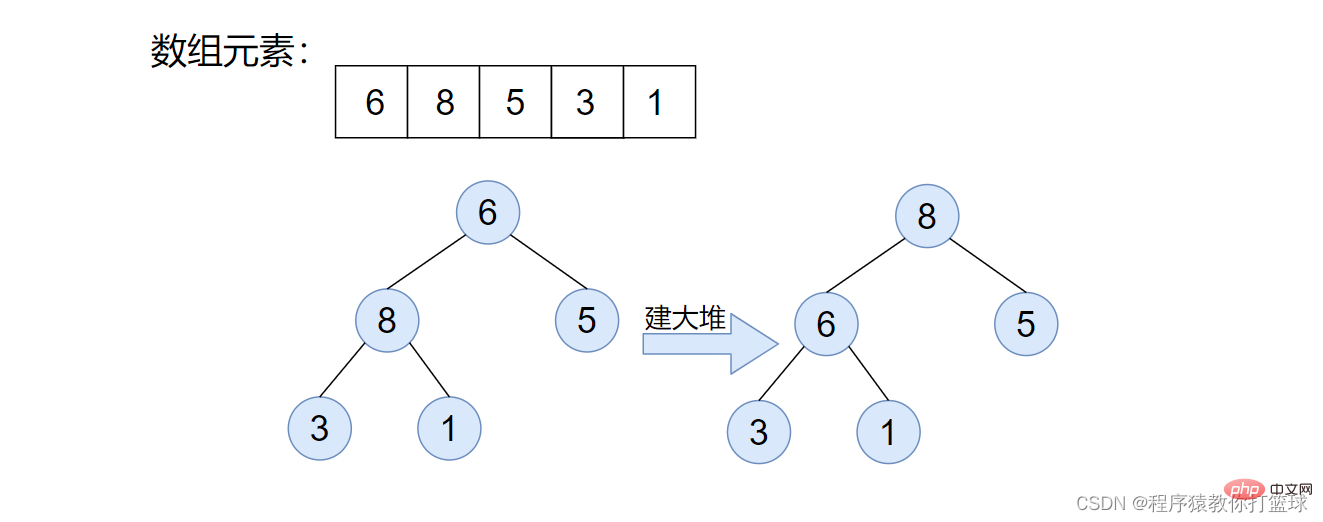
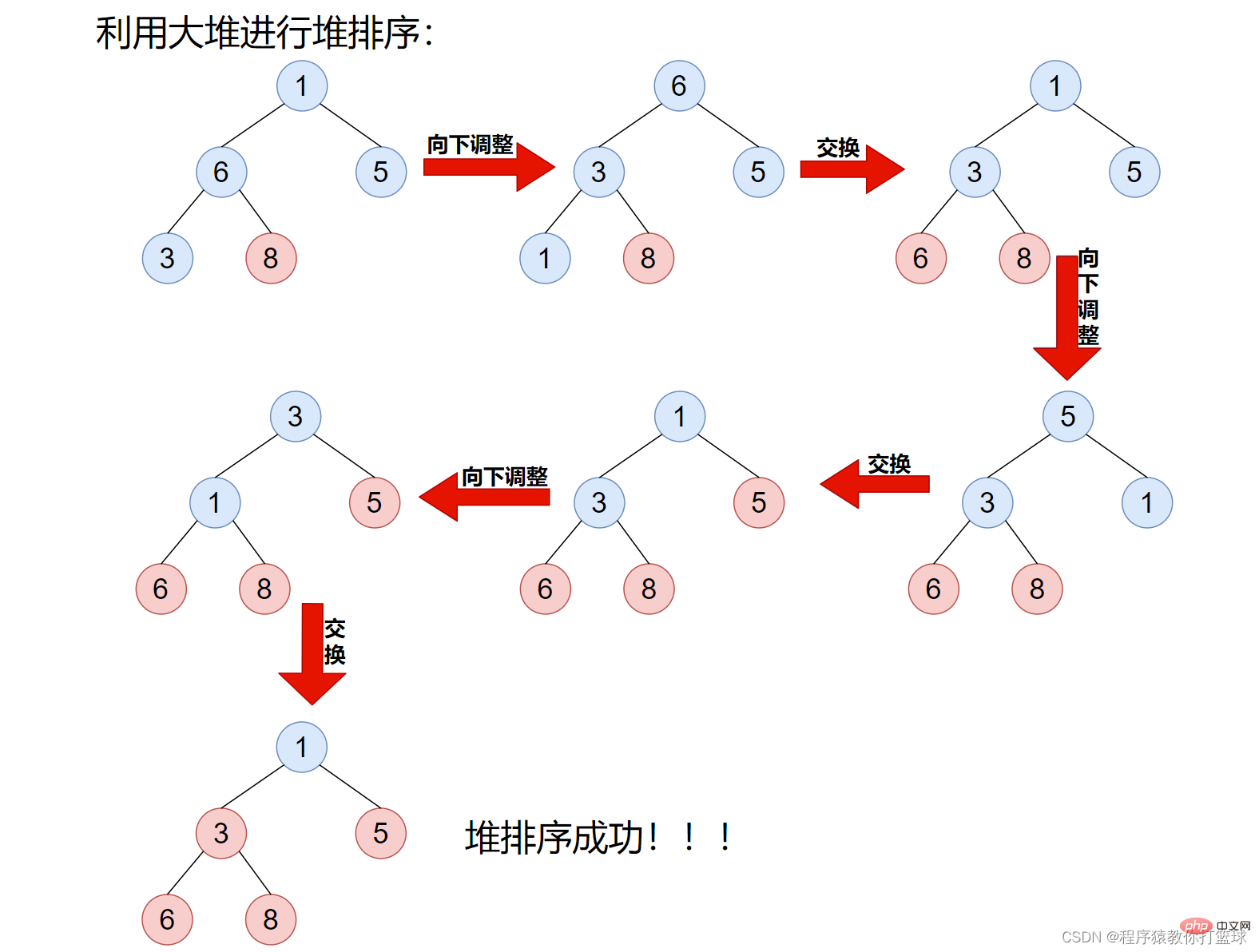
如上图步骤也很简单，先是将数组建成大堆，然后利用大堆来进行堆排序，首先将堆顶元素和最后一个元素交换，由此最大的元素就有序了，接着将该堆进行向下调整，使继续满足大堆性质，依次进行下去即可。

代码实现：

public void heapSort(int[] array) {
    // 建大堆 从最后一个非叶子节点开始向下调整
    // 非叶子节点下标 = (孩子节点下标 - 1) / 2
    for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {
        shiftDown(array, parent, array.length);
    }
    // 建大堆完成后, 每次堆顶元素与最后一个元素交换, 锁定最大元素的位置
    for (int len = array.length - 1; len > 0; len--) {
        swap(array, 0, len); //根节点与最后一个元素交换
        shiftDown(array, 0, len); //根节点位置向下调整
    }
}
private void shiftDown(int[] array, int parent, int len) {
    int child = parent * 2 + 1;
    while (child < len) {
        if (child + 1 < len && array[child + 1] > array[child]) {
            child++;
        }
        // 判断父节点是否大于较大的孩子节点
        if (array[parent] < array[child]) {
            swap(array, parent, child);
            // 更新下标的位置
            parent = child;
            child = parent * 2 + 1;
        } else {
            return;
        }
    }
}

• 时间复杂度分析：建堆的时间复杂度优先级队列那期有说过为 O(n)，排序调整堆的时候，一共要调整 n-1 次，每次向下调整的时间复杂度是 logn，所以即 logn(n - 1)，即 O(n*logn)，加上面建堆的时间复杂度：O(n) + O(n*logn)，最终时间复杂度也就是：O(n*logn)。
• 空间复杂度分析：O(1)
• 稳定性：不稳定

推荐学习：《java视频教程》

以上がJava データ構造の一般的な並べ替えアルゴリズム (概要共有)の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。