知識を増やしましょう!論理ルールを使用した機械学習
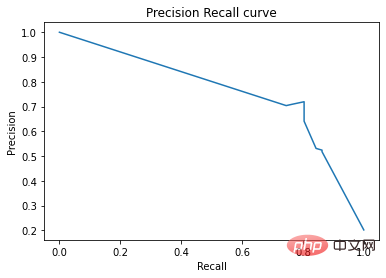
適合率-再現率曲線では、同じ点が異なる座標軸でプロットされます。警告: 左側の最初の赤い点 (再現率 0%、精度 100%) は 0 ルールに対応します。左側の 2 番目のドットが最初のルール、というように続きます。
Skope-rules はツリー モデルを使用してルール候補を生成します。まず、いくつかのデシジョン ツリーを構築し、ルート ノードから内部ノードまたはリーフ ノードまでのパスをルール候補として検討します。これらの候補ルールは、適合率や再現率などの事前定義された基準によってフィルタリングされます。精度と再現率がしきい値を超えるものだけが保持されます。最後に、類似性フィルタリングを適用して、十分な多様性を持つルールを選択します。一般に、スコープ ルールは、各根本原因の基礎となるルールを学習するために適用されます。
プロジェクト アドレス: https://github.com/scikit-learn-contrib/skope-rules
- Skope-rules はビルドですscikit-learn 上の Python 機械学習モジュール。3 条項 BSD ライセンスに基づいてリリースされています。
- Skope-rules は、ターゲット カテゴリを「定義」するための論理的で解釈可能なルールを学習すること、つまり、そのカテゴリのインスタンスを高精度で検出することを目的としています。
- スコープ ルールは、デシジョン ツリーの解釈可能性とランダム フォレストのモデリング機能の間のトレードオフです。
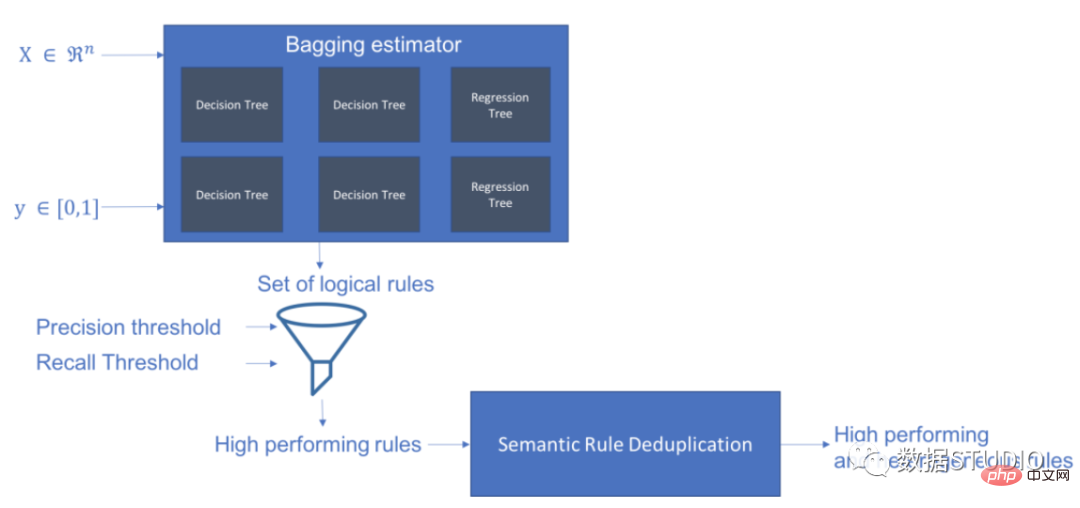
スキーマ
インストール
pipを使用して最新のリソースを取得できます:
pip install skope-rules
クイック スタート
SkopeRules は、論理ルールを使用してクラスを記述するために使用できます。
from sklearn.datasets import load_iris
from skrules import SkopeRules
dataset =load_iris()
feature_names = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
clf = SkopeRules(max_ Depth_duplicatinotallow=2,
n_estimators=30,
precision_min=0.3 ,
recall_min=0.1,
feature_names=feature_names)
for idx、enumerate(dataset.target_names) の種:
X、y = dataset.data、データセット。 target
clf.fit(X, y == idx)
rules = clf.rules_[0:3]
print("アヤメのルール", Species)
ルール内のルール:
print(ルール)
print()
print(20*'=')
print()

注:
次のエラーが表示される場合:

解決策:
Python インポート エラーについて: 名前 'six' を 'sklearn.externals' からインポートできませんYun Duojun on Stack Overflow で同様の質問が見つかりました: https://stackoverflow.com/questions/61867945/
解決策は次のとおりです
import six
import sys
sys.modules['sklearn .externals.six'] = six
import mlrose
個人テストは有効です。
SkopeRules は、「score_top_rules」メソッドを使用する場合、予測子としても使用できます。
from sklearn.datasets import load_boston
from sklearn.metrics import precision_recall_curve
from matplotlib import pyplot as plt
from skrules import SkopeRules
dataset =load_boston()
clf = SkopeRules(max_ Depth_duplicatinotallow=None,
n_estimators=30,
precision_min=0.2,
remember_min=0.01 ,
feature_names=dataset.feature_names)
XX, y = dataset.data, dataset.target > 25
X_train, y_train = X[:len(y)//2], y [:len(y)//2]
#X_test, y_test = X[len(y)//2:], y[len(y)//2:]
clf.fit(X_train, y_train )
y_score = clf.score_top_rules(X_test) # 各テスト例のリスク スコアを取得します
precision, recall, _ = precision_recall_curve(y_test, y_score)
plt.plot(recall, precision)
plt.xlabel('リコール')
plt.ylabel('精度')
plt.title('精度リコール曲線')
plt.show()
実用的なケース
このケースでは、有名なタイタニック号のデータ セットに対するスコープ ルールの使用を示します。
スコープルールの適用性:
- 2 分類問題の解決
- 解釈可能な決定ルールの抽出
このケースは 5 つの部分に分かれています
- 関連ライブラリのインポート
- データの準備
- モデルのトレーニング (ScopeRules().score_top_rules() メソッドを使用)
- 「サバイバル ルール」の説明 (SkopeRules().rules_property を使用)。
- パフォーマンス分析 (SkopeRules.predict_top_rules() メソッドを使用)。
from skrules import SkopeRules
# ライブラリのインポート
import pandas as pd
from sklearn.ensemble import GradientBoostingClassifier、RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve、precision_recall_curve
from matplotlib import cm
import numpy as np
from sklearn.metrics import infection_matrix
from IPython.display import display
# タイタニック号のデータをインポート
data = pd.read_csv('../ data/titanic-train.csv')
データ準備
data = data.query('Age == Age')
# は変数 Sex はエンコードされた値
data['is Female'] = (data['Sex'] == '女性') * 1
# 変数 Embarked はエンコードされた値
data = pd を作成します。 concat(
[data,
pd.get_dummies(data.loc[:,'Embarked'],
dummy_na=False,
prefix='Embarked',
prefix_sep='_' )],
axis=1
)
# 未使用の変数を削除
data = data.drop(['Name', 'Ticket', 'Cabin',
'PassengerId', ' Sex ', 'Embarked'],
axis = 1)
# トレーニング セットとテスト セットを作成します
XX_train, X_test, y_train, y_test = train_test_split(
data.drop(['Survived'], axis =1)、
data['Survived']、
test_size=0.25、random_state=42)
feature_names = X_train.columns
print('列名は次のとおりです: ' ' ' . join(feature_names.tolist()) '.')
print('トレーニング セットの形状は次のとおりです: ' str(X_train.shape) '.')
列名は次のとおりです: Pclass Age SibSp Parch料金
is Female Embarked_C Embarked_Q Embarked_S.
トレーニング セットの形状: (535, 9).
モデル トレーニング
gradient_boost_clf = GradientBoostingClassifier(random_state=42, n_estimators=30, max_ Depth = 5)
gradient_boost_clf.fit(X_train, y_train)
# ベンチマーク用のランダム フォレスト分類器をトレーニングする
random_forest_clf = RandomForestClassifier(random_state= 42、n_estimators=30、max_ Depth = 5)
random_forest_clf.fit(X_train, y_train)
# ベンチマーク用のデシジョン ツリー分類器をトレーニングする
decion_tree_clf = DecisionTreeClassifier(random_state=42, max_ Depth = 5)
decion_tree_clf.fit(X_train, y_train)
# skope-rules ブースティング分類器をトレーニングする
skope_rules_clf = SkopeRules(feature_names=feature_names, random_state= 42, n_estimators=30,
remember_min= 0.05, precision_min=0.9,
max_samples=0.7,
max_ Depth_duplicatinotallow= 4, max_ Depth = 5)
skope_rules_clf.fit(X_train, y_train)
# 予測スコアの計算
gradient_boost_scoring = gradient_boost_clf.predict_proba(X_test)[:, 1]
random_forest_scoring = random_forest_clf.predict_proba(X_test)[:, 1]
decion_tree_scoring = Decision_tree_clf.predict_proba( X_test)[:, 1]
skope_rules_scoring = skope_rules_clf.score_top_rules(X_test)
「生存ルール」の抽出
print("SkopeRules で作成" str(len( skope_rules_clf.rules_)) "rules n")
# Print these rules
rules_explanations = [
"3 歳未満および 37 歳未満、第 1 クラスまたは第 2 クラスの女性。 "
"1 等または 2 等で旅行し、26 ユーロ以上を支払う 3 歳以上の女性。 "
"1 等または 2 等で旅行し、29 ユーロ以上支払う女性。 "
"1 等または 2 等で旅行する 39 歳以上の女性。 "
]
print('最も優れた 4 つの「タイタニック生存ルール」は次のとおりです:/n')
for i_rule, rules in enumerate(skope_rules_clf.rules_[:4] )
print(rule[0])
print('->' rules_explanations[i_rule] 'n')
9 個のルールが SkopeRules を使用して作成されました。
そのうち上位 4 個は "タイタニック サバイバル ルール」は次のとおりです:
年齢 2.5
および Pclass 0.5
-> 3 歳未満の女性および37 歳未満、1 等または 2 等
年齢 > 2.5、運賃 > 26.125
、Pclass 0.5
-> 3 歳以上の女性1 等または 2 等で旅行し、26 ユーロ以上支払う老人。
運賃 > 29.356250762939453
and Pclass 0.5
-> 1 等または 2 等に乗車し、29 ユーロ以上支払う女性。
年齢 > 38.5 かつ Pclass and is女性 > 0.5
-> 39 歳以上で、1 等または 2 等で旅行する女性。
def compute_y_pred_from_query(X, ルール):
score = np.zeros(X.shape[0])#XX = X.reset_index(drop=True)
score[list( X.query(rule).index)] = 1
return(score)
def compute_performances_from_y_pred(y_true, y_pred,index_name='default_index'):
df = pd.DataFrame(data=
{
'精度':[sum(y_true * y_pred)/sum(y_pred)],
'再現率':[sum(y_true * y_pred)/sum(y_true)]
},
index=[index_name],
columns=['precision', 'recall']
)
return(df)
def compute_train_test_query_performances(X_train, y_train, X_test, y_test) 、ルール):
y_train_pred = compute_y_pred_from_query(X_train, ルール)
y_test_pred = compute_y_pred_from_query(X_test, ルール)
パフォーマンス = なし
パフォーマンス = pd.concat([
パフォーマンス,
compute_パフォーマンス_from_y_pred(y_train, y_train_pred, 'train_set')],
axis=0)
パフォーマンス = pd.concat([
パフォーマンス,
compute_performances_from_y_pred(y_test, y_test_pred, ' test_set')],
axis=0)
return(パフォーマンス)
print('Precision = 0.96 は、ルールによって決定された人々の 96% が生存者であることを意味します。 ')
print('Recall = 0.12 は、ルールによって特定された生存者が生存者の総数 n の 12% を占めることを意味します')
for i in range(4):
print ('ルール ' str (i 1) ':')
display(compute_train_test_query_performances(X_train, y_train,#XX_test, y_test,
skope_rules_clf.rules_[i][0])
)
精度 = 0.96 は、ルールによって決定された人々の 96% が生存者であることを意味します。 Recall = 0.12 は、ルールによって特定された生存者が全生存者の 12% を占めることを意味します。
 モデル パフォーマンスの検出
モデル パフォーマンスの検出
def Lot_titanic_scores(y_true,scores_with_line=[],scores_with_points=[],
labels_with_line=['Gradientブースティング'、'ランダム フォレスト'、'デシジョン ツリー'],labels_with_points=['skope-rules']):
gradient = np.linspace(0, 1, 10)
color_list = [ cm .tab10(x) for x (勾配の x ) ]
fig, axes = plt.subplots(1, 2, figsize=(12, 5),
sharex=True, sharey=True)
ax = axes[0]
n_line = 0
i_score、enumerate(scores_with_line) のスコア:
n_line = n_line 1
fpr, tpr, _ = roc_curve(y_true, スコア)
ax.plot(fpr, tpr, linestyle='-.', c=color_list[i_score], lw=1, label=labels_with_line[i_score])
i_score の場合、enumerate(scores_with_points):
fpr のスコア、tpr、_ = roc_curve(y_true, スコア)
ax.scatter(fpr[:-1], tpr[:-1], c=color_list[n_line i_score], s=10, label=labels_with_points[i_score] )
ax.set_title("ROC", fnotallow=20)
ax.set_xlabel('偽陽性率', fnotallow=18)
ax.set_ylabel('真陽性率 (リコール)', fnotallow =18)
ax.legend(loc='下中央', fnotallow=8)
ax = axes[1]
n_line = 0
i_score の場合、enumerate のスコア(scores_with_line) ):
n_line = n_line 1
精度、リコール、_ = precision_recall_curve(y_true、スコア)
ax.step(リコール、精度、linestyle='-.'、c=color_list[i_score]、lw =1、where='post'、label=labels_with_line[i_score])
i_score の場合、enumerate(scores_with_points) のスコア:
precision、recall、_ = precision_recall_curve(y_true、score)
ax.scatter (リコール, 精度, c=color_list[n_line i_score], s=10, label=labels_with_points[i_score])
ax.set_title("精度-リコール", fnotallow=20)
ax.set_xlabel('リコール(真陽性率)', fnotallow=18)
ax.set_ylabel('精度', fnotallow=18)
ax.legend(loc='中央下', fnotallow=8)
plt.show ()
plot_titanic_scores(y_test,
scores_with_line=[gradient_boost_scoring,random_forest_scoring,decion_tree_scoring],
scores_with_points=[skope_rules_scoring]
)
##ROC 曲線上で、各赤い点は、(skope-rules からの) アクティブ化されたルールの数に対応します。たとえば、最低点は 1 つのルールの結果ポイント (最高) です。 2 番目に低いポイントは 2 ルール結果ポイント、以下同様です。 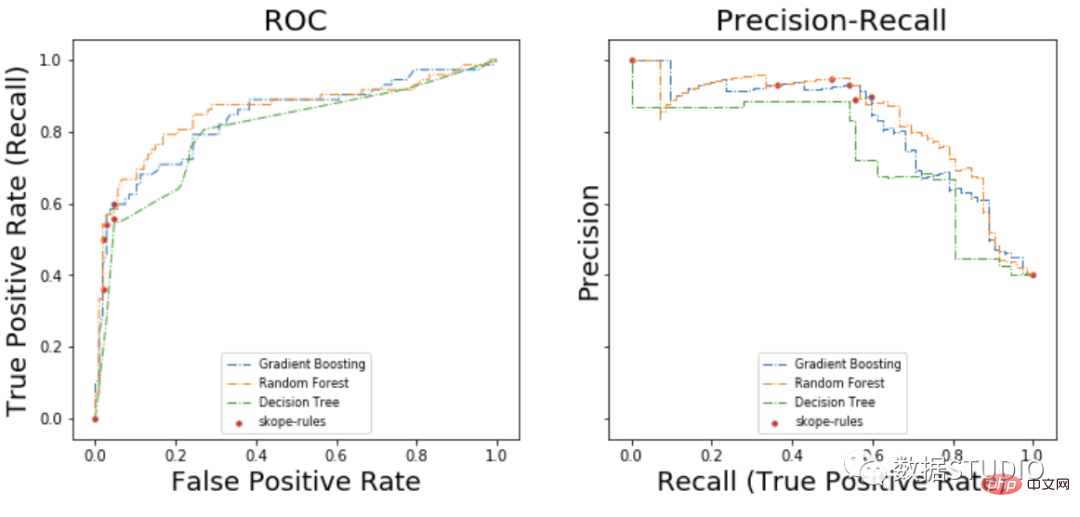
- skope-rules はデシジョン ツリーよりも優れたパフォーマンスを発揮します。
- skope-rules のパフォーマンスは、ランダム フォレスト/勾配ブースティング (この例では) と似ています。
- 4 つのルールを使用すると、非常に優れたパフォーマンス (再現率 61%、精度 94%) を達成できます (この例では)。
n_rule_chosen = 4
y_pred = skope_rules_clf.predict_top_rules(X_test, n_rule_chosen)
print('「 str(n_rule_chosen) 」で検出されたルールで到達したパフォーマンスは次のとおりです。 ')
compute_performances_from_y_pred(y_test, y_pred, 'test_set')
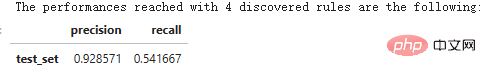
predict_top_rules(new_data, n_r) メソッドは、最初の n_r を含む new_data の予測を計算するために使用されます。アイテムのスコープルールルール。
以上が知識を増やしましょう!論理ルールを使用した機械学習の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7500
7500
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 52
52
 OpenOOD アップデート v1.5: 包括的かつ正確な配布外検出コード ライブラリとテスト プラットフォーム、オンライン ランキングとワンクリック テストをサポート
Jul 03, 2023 pm 04:41 PM
OpenOOD アップデート v1.5: 包括的かつ正確な配布外検出コード ライブラリとテスト プラットフォーム、オンライン ランキングとワンクリック テストをサポート
Jul 03, 2023 pm 04:41 PM
配布外 (OOD) の検出は、オープンワールドのインテリジェント システムの信頼性の高い動作に不可欠ですが、現在のオブジェクト指向の検出方法では「評価の不一致」(評価の不一致) が発生します。以前の作品 OpenOODv1 は OOD 検出の評価を統合しましたが、スケーラビリティと使いやすさには依然として制限がありました。最近、開発チームは OpenOODv1.5 を再度提案し、以前のバージョンと比較して、新しい OOD 検出手法の評価は、精度の確保、標準化、使いやすさの点で大幅に改善されました。イメージペーパー: https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
 知識を増やしましょう!論理ルールを使用した機械学習
Apr 01, 2023 pm 10:07 PM
知識を増やしましょう!論理ルールを使用した機械学習
Apr 01, 2023 pm 10:07 PM
適合率-再現率曲線では、同じ点が異なる軸でプロットされます。警告: 左側の最初の赤い点 (再現率 0%、精度 100%) は 0 ルールに対応します。左側の 2 番目のドットが最初のルール、というように続きます。 Skope-rules は、ツリー モデルを使用してルール候補を生成します。まず、いくつかのデシジョン ツリーを構築し、ルート ノードから内部ノードまたはリーフ ノードまでのパスをルール候補として検討します。これらの候補ルールは、適合率や再現率などの事前定義された基準によってフィルタリングされます。精度と再現率がしきい値を超えるものだけが保持されます。最後に、類似性フィルタリングを適用して、十分な多様性を持つルールを選択します。一般に、スコープ ルールは、それぞれの根本原因を学習するために適用されます。
 Javaのランタイムによって提供されるパラメータの数を確認するにはどうすればよいですか?
Sep 23, 2023 pm 01:13 PM
Javaのランタイムによって提供されるパラメータの数を確認するにはどうすればよいですか?
Sep 23, 2023 pm 01:13 PM
Java では、実行時にパラメータを渡す 1 つの方法は、コマンド ラインまたはターミナルを使用することです。コマンド ライン パラメーターのこれらの値を取得する場合、実行時にユーザーが指定したパラメーターの数を見つける必要がある場合があります。これは、length 属性を使用して実現できます。この記事は、サンプル プログラムを使用して、ユーザーが指定した数のパラメーターを渡したり取得したりするプロセスを説明することを目的としています。実行時にユーザーが指定した引数の数を取得する コマンド ライン引数の数を調べる前に、最初のステップとして、ユーザーが実行時に引数を渡せるようにするプログラムを作成します。 String[] パラメータ Java プログラムを作成するとき、main() メソッドに遭遇することがよくあります。 JVM がこのメソッドを呼び出すと、Java アプリケーションが実行を開始します。 String[]args という引数とともに使用されます。
 Linuxコマンド:Telnetプロセス数の確認方法
Mar 01, 2024 am 11:39 AM
Linuxコマンド:Telnetプロセス数の確認方法
Mar 01, 2024 am 11:39 AM
Linux コマンドは、システム管理者の日常業務に欠かせないツールの 1 つであり、さまざまなシステム管理タスクの実行に役立ちます。運用保守作業では、問題を検出して適時に調整するために、システム内の特定のプロセスの番号を確認する必要がある場合があります。この記事では、Linuxコマンドを使用してTelnetプロセス数を確認する方法を紹介しますので、一緒に学びましょう。 Linux システムでは、ps コマンドと grep コマンドを組み合わせて使用すると、Telnet プロセスの数を表示できます。まず、ターミナルを開く必要があります。
 C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
C++ を使用して、同じ最小値と最大値を持つ部分配列の数を見つけるコードを作成します。
Aug 25, 2023 pm 11:33 PM
この記事では、C++ を使用して、最大値と最小値が同じ部分配列の数を求める問題を解決します。以下は問題の例です。 -入力:array={2,3,6,6,2,4,4,4}出力:12説明:{2},{3},{6},{6}, {2 }、{4}、{4}、{4}、{6,6}、{4,4}、{4,4}、および {4,4,4} は、同じ最大要素と最小要素で形成できるサブ配列です。入力: 配列 = {3, 3、1、5、
 C++ を使用して N 分ツリーを走査する方法の数を求めます。
Sep 04, 2023 pm 05:01 PM
C++ を使用して N 分ツリーを走査する方法の数を求めます。
Sep 04, 2023 pm 05:01 PM
N 分ツリーが与えられた場合、私たちのタスクは、ツリーを横断する方法の合計数を見つけることです。例: 上記のツリーの場合、出力は 192 になります。この問題を解決するには、組み合わせ論の知識が必要です。この問題では、各パスの可能な組み合わせをすべてチェックするだけで答えが得られます。解を見つける方法 この方法では、階層の走査を実行し、各ノードが持つ子の数を確認し、その答えを階乗的に乗算するだけです。上記のメソッド #include<bits/stdc++.h>usingnamespacestd;structNode{//s の C++ コード例
 二分木内の二等辺三角形の数
Sep 05, 2023 am 09:41 AM
二分木内の二等辺三角形の数
Sep 05, 2023 am 09:41 AM
バイナリ ツリーは、各ノードが最大 2 つの子ノードを持つことができるデータ構造です。これらの子は、それぞれ左の子と右の子と呼ばれます。親の配列表現が与えられたとします。それを使用してバイナリ ツリーを作成する必要があります。二分木には複数の二等辺三角形が含まれる場合があります。この二分木で可能な二等辺三角形の総数を見つけなければなりません。この記事では、C++ でこの問題を解決するためのいくつかの手法を検討します。問題を理解すると、親配列が得られます。配列インデックスがツリー ノードの値を形成し、配列内の値がその特定のインデックスの親ノードを与えるように、それをバイナリ ツリーの形式で表す必要があります。 -1 は常にルートの親であることに注意してください。以下に、配列とそのバイナリ ツリー表現を示します。親配列=[0,-1,3,1,
 C++ を使用して、合計が奇数の部分配列の数を見つけるコードを作成します。
Sep 21, 2023 am 08:45 AM
C++ を使用して、合計が奇数の部分配列の数を見つけるコードを作成します。
Sep 21, 2023 am 08:45 AM
サブ配列は配列の連続した部分です。たとえば、配列 [5,6,7,8] を考えると、(5)、(6)、(7)、(8)、(5,6)、などの 10 個の空ではないサブ配列があります。 (6, 7)、(7,8)、(5,6,7)、(6,7,8)、(5,6,7,8)。このガイドでは、奇数の合計を持つ部分配列の数を見つけるために C++ で考えられるすべての情報を説明します。奇数和の部分配列の数を見つけるには、さまざまな方法を使用できます。ここでは簡単な例を示します。入力:配列={9,8,7,6,5}出力:9説明:Sumofsubarray-{9}= 9{7




