因果の森アルゴリズムに基づく意思決定測位アプリケーション
翻訳者 | 朱賢中
査読者|孫樹娟
前回の ブログ では、因果ツリーを使用してポリシーの異質性を評価する方法を 説明しました 処理## ####効果######。 #読んでいない場合は、## を読んでからこの記事を読むことをお勧めします。この記事の と思います この記事の の の部分と、これに関連する の内容を理解しました。記事。 なぜ不均一な治療効果 (HTE: 異質な治療効果) なのでしょうか?まず、異種の 治療 効果を推定することで、予期される結果 (病気、会社の収益、顧客満足度など) に基づいて
彼らの を条件付けることができます。 .) 処理 (医薬品、広告、製品など) を提供することを選択したユーザー (患者、ユーザー、顧客など)。言い換えれば、HTE はターゲット設定において # に役立つと推定されます。実際、この記事の後半で 参照 するように、1 つの processing メソッドは一部のユーザーに良い結果をもたらしています。平均すると効果がないか、逆効果になる可能性さえあります。逆もまた真である可能性があります: ある薬は平均して効果がありますが、は私たちが明確であればユーザーには副作用があります。情報があれば#この薬の有効性はさらに改善されます。 #この記事では、因果ツリーの拡張である因果 forest フォレストを検討します。ランダム フォレストが複数の ブートストラップ ツリー を平均して回帰ツリーを拡張するのと同じように、コーサル フォレストも因果ツリーを拡張します。主な違いは推論の観点から生じますが、推論はそれほど単純ではありません。また、さまざまな HTE 推定アルゴリズムの出力を比較する方法と、それらを政策目標にどのように使用できるかについても説明します。
オンライン割引ケースこの記事の残りの部分では、前回の記事を引き続き使用します。 原因と結果ツリーの記事で使用されているおもちゃの例: オンライン ストアであると仮定して、新規顧客に割引を提供することで店舗での支出が増加するかどうかを知りたいとします。
割引がお買い得かどうかを理解するために、次のランダム化実験、つまり A/B テストを実施しました。新規顧客がオンライン ストアを閲覧するたびに、ランダムに ## に割り当てます。 # 治療 状態。 処理された;ユーザーには割引を提供しますが、管理しているユーザーには割引を提供しません。データ生成プロセス dgp_online_discounts() を ファイル src.dgp からインポートします。また、いくつかの描画関数とライブラリを src.utilslibraries からインポートします。コードだけでなくデータやテーブルも含めるために、、Jupyter ベースの である Deepnote フレームワーク を使用しました。 Web の共同ノートブック環境。
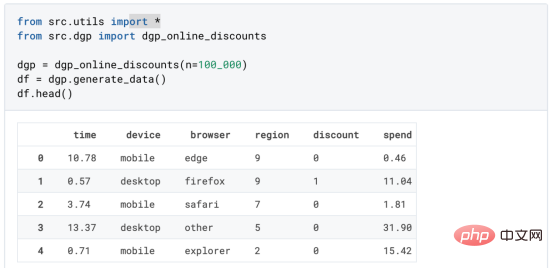 当社には 100,000 人のオンライン Cstore 訪問者に関するデータがあり、彼らが Web サイトにアクセスした時間と使用するデバイスを観察しています。 . 、ブラウザー、および地理的地域。また、
当社には 100,000 人のオンライン Cstore 訪問者に関するデータがあり、彼らが Web サイトにアクセスした時間と使用するデバイスを観察しています。 . 、ブラウザー、および地理的地域。また、
顧客が割引を受けられたかどうか、我々がそれをどのように処理したのか、、彼らがいくら使ったか、# # も観察します。 # およびその他の興味深い 結果 。 実験はランダムに割り当てられるため、単純な平均差推定値を使用して ## を推定できます。 #実験
効果。 実験 グループとコントロール グループは、割引を除いて類似していると予想されるため、支出額の差異は割引によるものと考えられます。 割引
が有効であるようです: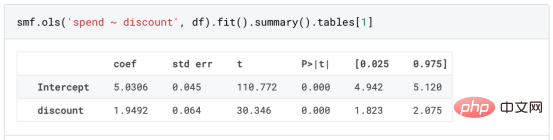 実験
実験
平均支出額は 1.95 ドル増加しました。しかし、すべての顧客が平等に影響を受けるのでしょうか? この質問に答えるために、異種混合の 治療効果## を推定したいと思います。 #、おそらく個人レベルです。
コーザルフォレスト 計算異種治療効果さまざまなオプションがあります。最も単純なアプローチは、異質性の次元の観点から対象の結果を操作することです。このアプローチの問題は、どの変数を選択するかです。場合によっては、事前に
行動の指針となる情報を 持っていることがあります。たとえば、モバイル ユーザーの平均支出額がデスクトップ ユーザーの多くよりも高いことがわかっている場合があります。また、商業上の理由から特定の分野に興味がある場合もあります。たとえば、特定の地域にさらに投資したい場合などです。ただし、追加情報がない場合は、プロセスをデータ主導型にする必要があります。前回の記事では、不均一な治療効果を推定するためのデータ主導型アプローチについて検討しました。因果関係の木。次に、それらを因果の森に拡張します。ただし、始める前に、その因果関係のない親戚であるランダム フォレストを紹介する必要があります。
ランダム フォレストは、その名前が示すように、回帰ツリーの拡張であり、ランダム性の 2 つの独立したソースを回帰ツリーに追加します。特に、ランダム フォレスト アルゴリズム は、ブートストラップ サンプルを使用して、さまざまな回帰ツリーで予測を行うことができます。 トレーニングを実行します。そしてそれらを合計して平均します。このプロセスは、ガイド付き集計アルゴリズム (バギング アルゴリズムとも呼ばれる) と呼ばれることが多く、任意の予測アルゴリズムに適用でき、ランダム フォレストに固有のものではありません。追加のランダム性の原因は、特徴の選択からもたらされます。これは、各分割で、すべての特徴 X のランダムなサブセットのみが最適な分割として考慮されるためです。
#これら 2 つの追加のランダム性ソースは非常に重要であり、ランダム フォレストのパフォーマンスの向上に役立ちます。まず、バギング アルゴリズムにより、ランダム フォレストは複数の離散予測を平均することで回帰ツリーよりも滑らかな予測を生成できます。対照的に、ランダムな特徴選択により、ランダム フォレストは特徴空間をより深く探索できるようになり、単純な回帰ツリーよりも多くの相互作用を発見できるようになります。実際、変数間には、それ自体では予測性があまり高くない (したがって意見を分裂させることはない) ものの、組み合わせると非常に強力な相互作用が存在する可能性があります。コーザル フォレストはランダム フォレストと同等ですが、コーザル ツリーとは異なり、
異種の治療効果を推定するために使用されます。回帰木とまったく同じです。因果関係ツリーと同様に、私たちには基本的な問題があります。それは、私たちが観察していないオブジェクト、つまり個々の 治療効果τᵢ を予測することに興味があるということです。解決策は、各観測値の期待値がまさに processing 効果である補助結果変数 Y* を作成することです。
補助結果変数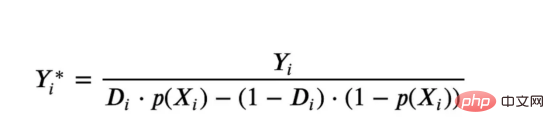
さらに詳しく知りたい場合は、
なぜこの変数が個人に影響を及ぼさないのか治療法バイアスを加える 私の前の記事 をご覧ください。私はここにいます## A detailed の紹介は # 件の記事で行われます。つまり、Yᵢ* を 1 つの観測値の平均差の推定量として考えることができます。 結果変数を取得したら、ランダム フォレストを使用して異種治療効果を推定するために、さらにいくつかのことを行う必要があります。まず、各リーフに同じ数の処理ユニットと制御ユニットを備えたツリーを構築する必要があります。次に、さまざまなサンプルを使用してツリーを構築し、それを評価する必要があります。つまり、各リーフの平均結果を計算します。このプロセスは、各葉のサンプルをツリー構造から独立したものとして扱うことができるため、正直ツリーと呼ばれることがあり、推論に非常に役立ちます。 評価を進める前に、まずカテゴリ変数デバイス、ブラウザ
および##のダミー変数を生成しましょう。 #地域 。 df_dummies = pd.get_dummies(df[dgp.X[1:]], drop_first=True)
df = pd.concat([df, df_dummies], axis=1)
X = ['time'] + list(df_dummies.columns)
を推定できるようになりました。幸いなことに、 は Microsoft の EconML パッケージですでに利用可能であるため、これらすべてを手動で行う必要はありません。 に適切な因果関係ツリーとフォレストの実装を提供します。 の
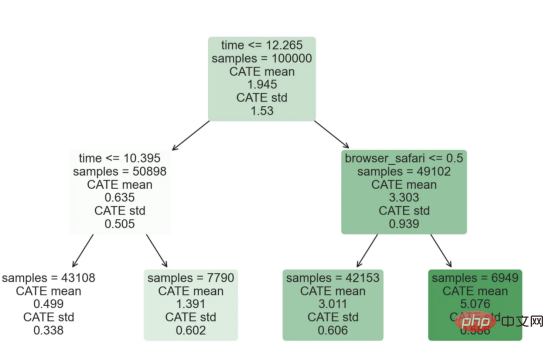
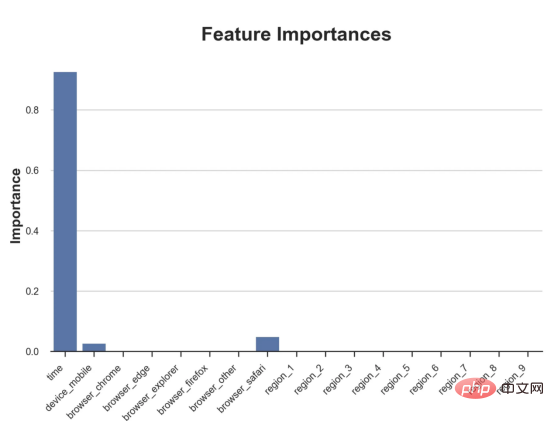
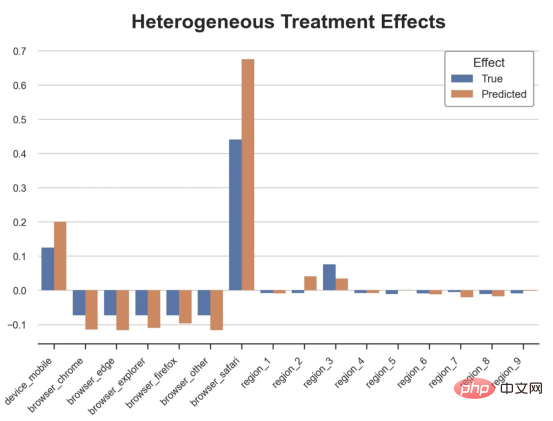
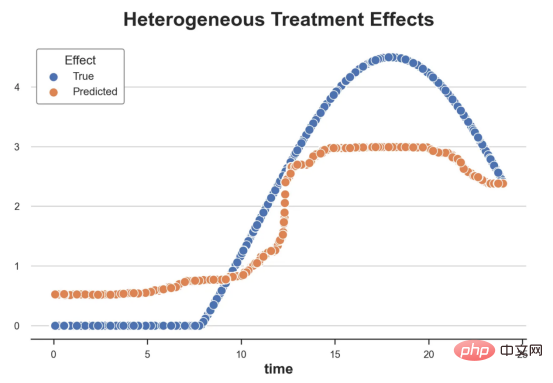
CausalForestML 関数を使用します。 与因果树不同,因果森林更难解释,因为我们无法可视化每一棵树。我们可以使用SingleTreeateInterpreter函数来绘制因果森林算法的等效表示。 因果森林模型表示 我们可以像因果树模型一样解释树形图。在顶部,我们可以看到数据中的平均$Y^*$的值为1.917$。从那里开始,根据每个节点顶部突出显示的规则,数据被拆分为不同的分支。例如,根据时间是否晚于11.295,第一节点将数据分成大小为46878$和53122$的两组。在底部,我们得到了带有预测值的最终分区。例如,最左边的叶子包含40191$的观察值(时间早于11.295,在非Safari浏览器环境下),我们预测其花费为0.264$。较深的节点颜色表示预测值较高。 这种表示的问题在于,与因果树的情况不同,它只是对模型的解释。由于因果森林是由许多自助树组成的,因此无法直接检查每个决策树。了解在确定树分割时哪个特征最重要的一种方法是所谓的特征重要性。 显然,时间是异质性的第一个维度,其次是设备(特别是移动设备)和浏览器(特别是Safari)。其他维度无关紧要。 现在,让我们检查一下模型性能如何。 通常,我们无法直接评估模型性能,因为与标准的机器学习设置不同,我们没有观察到实际情况。因此,我们不能使用测试集来计算模型精度的度量。然而,在我们的案例中,我们控制了数据生成过程,因此我们可以获得基本的真相。让我们从分析模型如何沿着数据、设备、浏览器和区域的分类维度估计异质处理效应开始。 对于每个分类变量,我们绘制了实际和估计的平均处理效果。 作者提供的每个分类值的真实和估计处理效果 因果森林算法非常善于预测与分类变量相关的处理效果。至于因果树,这是预期的,因为算法具有非常离散的性质。然而,与因果树不同的是,预测更加微妙。 我们现在可以做一个更相关的测试:算法在时间等连续变量下的表现如何?首先,让我们再次隔离预测的处理效果,并忽略其他协变量。 def compute_time_effect(df, hte_model, avg_effect_notime): 我们现在可以复制之前的数字,但时间维度除外。我们绘制了一天中每个时间的平均真实和估计处理效果。 沿时间维度绘制的真实和估计的处理效果 我们现在可以充分理解因果树和森林之间的区别:虽然在因果树的情况下,估计基本上是一个非常粗略的阶跃函数,但我们现在可以看到因果树如何产生更平滑的估计。 我们现在已经探索了该模型,是时候使用它了! 假设我们正在考虑向访问我们在线商店的新客户提供4美元的折扣。 折扣对哪些客户有效?我们估计平均处理效果为1.9492美元。这意味着,平均而言折扣并不真正有利可图。然而,现在可以针对单个客户,我们只能向一部分新客户提供折扣。我们现在将探讨如何进行政策目标定位,为了更好地了解目标定位的质量,我们将使用因果树模型作为参考点。 我们使用相同的CauselForestML函数构建因果树,但将估计数和森林大小限制为1。 接下来,我们将数据集分成一个训练集和一个测试集。这一想法与交叉验证非常相似:我们使用训练集来训练模型——在我们的案例中是异质处理效应的估计器——并使用测试集来评估其质量。主要区别在于,我们没有观察到测试数据集中的真实结果。但是我们仍然可以使用训练测试分割来比较样本内预测和样本外预测。 我们将所有观察结果的80%放在训练集中,20%放在测试集中。 首先,让我们仅在训练样本上重新训练模型。 现在,我们可以确定目标策略,即决定我们向哪些客户提供折扣。答案似乎很简单:我们向所有预期处理效果大于成本(4美元)的客户提供折扣。 借助于一个可视化工具,它可以让我们了解处理对谁有效以及如何有效,这就是所谓的处理操作特征(TOC)曲线。这个名字可以看作是基于另一个更著名的接收器操作特性(ROC)曲线的修正,该曲线描绘了二元分类器的不同阈值的真阳性率与假阳性率。这两种曲线的想法类似:我们绘制不同比例受处理人群的平均处理效果。在一个极端情况下,当所有客户都被处理时,曲线的值等于平均处理效果;而在另一个极端情况下,当只有一个客户被处理时曲线的值则等于最大处理效果。 现在让我们计算曲线。 现在,我们可以绘制两个CATE估算器的处理操作特征(TOC)曲线。 处理操作特性曲线 正如预期的那样,两种估算器的TOC曲线都在下降,因为平均效应随着我们处理客户份额的增加而降低。换言之,我们在发布折扣时越有选择,每个客户的优惠券效果就越高。我还画了一条带有折扣成本的水平线,以便我们可以将TOC曲线下方和成本线上方的阴影区域解释为预期利润。 这两种算法预测的处理份额相似,约为20%,因果森林算法针对的客户略多一些。然而,他们预测的利润结果却大相径庭。因果树算法预测的边际较小且恒定,而因果林算法预测的是更大且更陡的边际。那么,哪一种算法更准确呢? 为了比较它们,我们可以在测试集中对它们进行评估。我们采用训练集上训练的模型,预测处理效果,并将其与测试集上训练模型的预测进行比较。注意,与机器学习标准测试程序不同,有一个实质性的区别:在我们的案例中,我们无法根据实际情况评估我们的预测,因为没有观察到处理效果。我们只能将两个预测相互比较。 因果树模型似乎比因果森林模型表现得更好一些,总净效应为8386美元——相对于4948美元。从图中,我们也可以了解差异的来源。因果森林算法往往限制性更强,处理的客户更少,没有误报的阳性,但也有很多误报的阴性。另一方面,因果树算法看起来更加“慷慨”,并将折扣分配给更多的新客户。这既转化为更多的真阳性,也转化为假阳性。总之,净效应似乎有利于因果树算法。 通常,我们讨论到这里就可以停止了,因为我们可以做的事情不多了。然而,在我们的案例情形中,我们还可以访问真正的数据生成过程。因此,接下来我们不妨检查一下这两种算法的真实精度。 首先,让我们根据处理效果的预测误差来比较它们。对于每个算法,我们计算处理效果的均方误差。 结果是,随机森林模型更好地预测了平均处理效果,均方误差为0.5555美元,而不是0.9035美元。 那么,这是否意味着更好的目标定位呢?我们现在可以复制上面所做的相同的柱状图,以了解这两种算法在策略目标方面的表现。 这两幅图非常相似,但结果却大相径庭。事实上,因果森林算法现在优于因果树算法,总效果为10395美元,而非8828美元。为什么会出现这种突然的差异呢? 为了更好地理解差异的来源,让我们根据实际情况绘制TOC。 处理操作特性曲线。 正如我们所看到的,TOC是倾斜度非常大的,存在一些平均处理效果非常高的客户。随机森林算法能够更好地识别它们,因此总体上更有效,尽管目标客户较少些。 この記事では、関数非常に強力な##を学びました##異種治療効果を推定するためのアルゴリズム - 因果フォレスト。因果フォレストは因果ツリーと同じ原則に基づいて構築されますが、パラメーター空間のより深い探索と アルゴリズム の恩恵を受けます。 #さらに、私たちは 異質な治療効果の推定 # ポリシーを実装するために #ポジショニング #。最も高い 処理 効果を持つユーザーを特定することで、 ポリシーが収益性があることを 保証できます。また、分布の裾野の # が平均値 # よりも強い可能性があるため、政策目標が 異種治療効果 # 評価目標とは異なることもわかります。 ##相関######。 参考文献 S. Athey、G. Imbens、異種因果効果のための再帰的分割 (2016)、PNAS。 S. Wager, S. Athey、ランダム フォレストを使用した異種混合治療効果の推定と推論 (2018)、米国統計協会ジャーナル。 、Matteo Courthoud著from econml.dml import CausalForestDML
np.random.seed(0)
forest_model = CausalForestDML(max_depth=3)
forest_model = forest_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
from econml.cate_interpreter import SingleTreeCateInterpreter
intrp = SingleTreeCateInterpreter(max_depth=2).interpret(forest_model, df[X])
intrp.plot(feature_names=X, fnotallow=12)

性能
def compute_discrete_effects(df, hte_model):
temp_df = df.copy()
temp_df.time = 0
temp_df = dgp.add_treatment_effect(temp_df)
temp_df = temp_df.rename(columns={'effect_on_spend': 'True'})
temp_df['Predicted'] = hte_model.effect(temp_df[X])
df_effects = pd.DataFrame()
for var in X[1:]:
for effect in ['True', 'Predicted']:
v = temp_df.loc[temp_df[var]==1, effect].mean() - temp_df[effect][temp_df[var]==0].mean()
effect_var = {'Variable': [var], 'Effect': [effect], 'Value': [v]}
df_effects = pd.concat([df_effects, pd.DataFrame(effect_var)]).reset_index(drop=True)
return df_effects, temp_df['Predicted'].mean()
df_effects, avg_effect_notime = compute_discrete_effects(df, forest_model)fig, ax = plt.subplots()
sns.barplot(data=df_effects, x="Variable", y="Value", hue="Effect", ax=ax).set(
xlabel='', ylabel='', title='Heterogeneous Treatment Effects')
ax.set_xticklabels(ax.get_xticklabels(), rotatinotallow=45, ha="right");
df_time = df.copy()
df_time[[X[1:]] + ['device', 'browser', 'region']] = 0
df_time = dgp.add_treatment_effect(df_time)
df_time['predicted'] = hte_model.effect(df_time[X]) + avg_effect_notime
return df_time
df_time = compute_time_effect(df, forest_model, avg_effect_notime)
sns.scatterplot(x='time', y='effect_on_spend', data=df_time, label='True')
sns.scatterplot(x='time', y='predicted', data=df_time, label='Predicted').set(
ylabel='', title='Heterogeneous Treatment Effects')
plt.legend(title='Effect');
策略定位
cost = 4
from econml.dml import CausalForestDML
np.random.seed(0)
tree_model = CausalForestDML(n_estimators=1, subforest_size=1, inference=False, max_depth=3)
tree_model = tree_model.fit(Y=df[dgp.Y], X=df[X], T=df[dgp.D])
df_train, df_test = df.iloc[:80_000, :], df.iloc[20_000:,]
np.random.seed(0)
tree_model = tree_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
forest_model = forest_model.fit(Y=df_train[dgp.Y], X=df_train[X], T=df_train[dgp.D])
def compute_toc(df, hte_model, cost, truth=False):
df_toc = pd.DataFrame()
for q in np.linspace(0, 1, 101):
if truth:
df = dgp.add_treatment_effect(df_test)
effect = df['effect_on_spend']
else:
effect = hte_model.effect(df[X])
ate = np.mean(effect[effect >= np.quantile(effect, 1-q)])
temp = pd.DataFrame({'q': [q], 'ate': [ate]})
df_toc = pd.concat([df_toc, temp]).reset_index(drop=True)
return df_toc
df_toc_tree = compute_toc(df_train, tree_model, cost)
df_toc_forest = compute_toc(df_train, forest_model, cost)def plot_toc(df_toc, cost, ax, color, title):
ax.axhline(y=cost, lw=2, c='k')
ax.fill_between(x=df_toc.q, y1=cost, y2=df_toc.ate, where=(df_toc.ate > cost), color=color, alpha=0.3)
if any(df_toc.ate > cost):
q = df_toc_tree.loc[df_toc.ate > cost, 'q'].values[-1]
else:
q = 0
ax.axvline(x=q, ymin=0, ymax=0.36, lw=2, c='k', ls='--')
sns.lineplot(data=df_toc, x='q', y='ate', ax=ax, color=color).set(
title=title, ylabel='ATT', xlabel='Share of treated', ylim=[1.5, 8.5])
ax.text(0.7, cost+0.1, f'Discount cost: {cost:.0f}$', fnotallow=12)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6))
plot_toc(df_toc_tree, cost, ax1, 'C0', 'TOC - Causal Tree')
plot_toc(df_toc_forest, cost, ax2, 'C1', 'TOC - Causal Forest')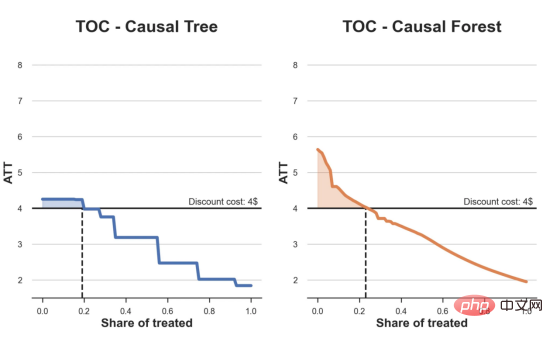
def compute_effect_test(df_test, hte_model, cost, ax, title, truth=False):
df_test['Treated'] = hte_model.effect(df_test[X]) > cost
if truth:
df_test = dgp.add_treatment_effect(df_test)
df_test['Effect'] = df_test['effect_on_spend']
else:
np.random.seed(0)
hte_model_test = copy.deepcopy(hte_model).fit(Y=df_test[dgp.Y], X=df_test[X], T=df_test[dgp.D])
df_test['Effect'] = hte_model_test.effect(df_test[X])
df_test['Cost Effective'] = df_test['Effect'] > cost
tot_effect = ((df_test['Effect'] - cost) * df_test['Treated']).sum()
sns.barplot(data=df_test, x='Cost Effective', y='Treated', errorbar=None, width=0.5, ax=ax, palette=['C3', 'C2']).set(
title=title + 'n', ylim=[0,1])
ax.text(0.5, 1.08, f'Total effect: {tot_effect:.2f}', fnotallow=14, ha='center')
return
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree')
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest')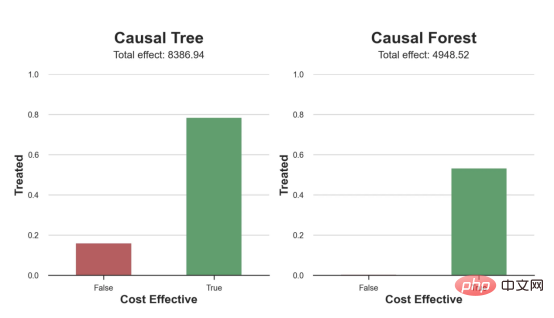
from sklearn.metrics import mean_squared_error as mse
def compute_mse_test(df_test, hte_model):
df_test = dgp.add_treatment_effect(df_test)
print(f"MSE = {mse(df_test['effect_on_spend'], hte_model.effect(df_test[X])):.4f}")
compute_mse_test(df_test, tree_model)
compute_mse_test(df_test, forest_model)fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
compute_effect_test(df_test, tree_model, cost, ax1, 'Causal Tree', True)
compute_effect_test(df_test, forest_model, cost, ax2, 'Causal Forest', True)
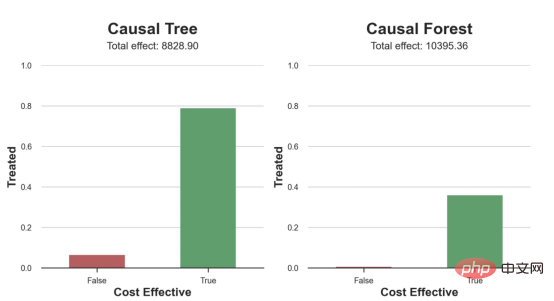
df_toc = compute_toc(df_test, tree_model, cost, True)
fix, ax = plt.subplots(1, 1, figsize=(7, 5))
plot_toc(df_toc, cost, ax, 'C2', 'TOC - Ground Truth')
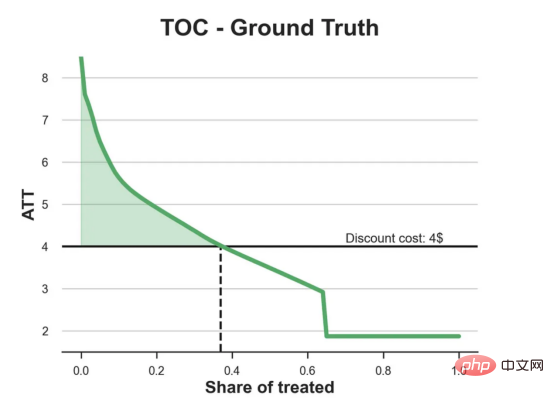
結論
以上が因果の森アルゴリズムに基づく意思決定測位アプリケーションの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7518
7518
 15
15
 1378
1378
 52
52
 81
81
 11
11
 21
21
 67
67
 この記事では、SHAP: 機械学習のモデルの説明について説明します。
Jun 01, 2024 am 10:58 AM
この記事では、SHAP: 機械学習のモデルの説明について説明します。
Jun 01, 2024 am 10:58 AM
機械学習とデータ サイエンスの分野では、モデルの解釈可能性が常に研究者や実務家に焦点を当ててきました。深層学習やアンサンブル手法などの複雑なモデルが広く適用されるようになったことで、モデルの意思決定プロセスを理解することが特に重要になってきました。 Explainable AI|XAI は、モデルの透明性を高めることで、機械学習モデルに対する信頼と自信を構築するのに役立ちます。モデルの透明性の向上は、複数の複雑なモデルの普及や、モデルを説明するための意思決定プロセスなどの方法によって実現できます。これらの方法には、特徴重要度分析、モデル予測間隔推定、ローカル解釈可能性アルゴリズムなどが含まれます。特徴重要度分析では、入力特徴に対するモデルの影響度を評価することで、モデルの意思決定プロセスを説明できます。モデルの予測間隔の推定
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
翻訳者 | Li Rui によるレビュー | 今日、人工知能 (AI) および機械学習 (ML) モデルはますます複雑になっており、これらのモデルによって生成される出力はブラックボックスになっており、関係者に説明することができません。 Explainable AI (XAI) は、利害関係者がこれらのモデルがどのように機能するかを理解できるようにし、これらのモデルが実際に意思決定を行う方法を確実に理解できるようにし、AI システムの透明性、信頼性、およびこの問題を解決するための説明責任を確保することで、この問題を解決することを目指しています。この記事では、さまざまな説明可能な人工知能 (XAI) 手法を検討して、その基礎となる原理を説明します。説明可能な AI が重要であるいくつかの理由 信頼と透明性: AI システムが広く受け入れられ、信頼されるためには、ユーザーは意思決定がどのように行われるかを理解する必要があります
 あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
あなたが知らない機械学習の 5 つの流派
Jun 05, 2024 pm 08:51 PM
機械学習は人工知能の重要な分野であり、明示的にプログラムしなくてもコンピューターにデータから学習して能力を向上させる機能を提供します。機械学習は、画像認識や自然言語処理から、レコメンデーションシステムや不正行為検出に至るまで、さまざまな分野で幅広く応用されており、私たちの生活様式を変えつつあります。機械学習の分野にはさまざまな手法や理論があり、その中で最も影響力のある 5 つの手法は「機械学習の 5 つの流派」と呼ばれています。 5 つの主要な学派は、象徴学派、コネクショニスト学派、進化学派、ベイジアン学派、およびアナロジー学派です。 1. 象徴主義は、象徴主義とも呼ばれ、論理的推論と知識の表現のためのシンボルの使用を強調します。この学派は、学習は既存の既存の要素を介した逆演繹のプロセスであると信じています。
 フラッシュ アテンションは安定していますか?メタとハーバードは、モデルの重みの偏差が桁違いに変動していることを発見しました
May 30, 2024 pm 01:24 PM
フラッシュ アテンションは安定していますか?メタとハーバードは、モデルの重みの偏差が桁違いに変動していることを発見しました
May 30, 2024 pm 01:24 PM
MetaFAIR はハーバード大学と協力して、大規模な機械学習の実行時に生成されるデータの偏りを最適化するための新しい研究フレームワークを提供しました。大規模な言語モデルのトレーニングには数か月かかることが多く、数百、さらには数千の GPU を使用することが知られています。 LLaMA270B モデルを例にとると、そのトレーニングには合計 1,720,320 GPU 時間が必要です。大規模なモデルのトレーニングには、これらのワークロードの規模と複雑さにより、特有のシステム上の課題が生じます。最近、多くの機関が、SOTA 生成 AI モデルをトレーニングする際のトレーニング プロセスの不安定性を報告しています。これらは通常、損失スパイクの形で現れます。たとえば、Google の PaLM モデルでは、トレーニング プロセス中に最大 20 回の損失スパイクが発生しました。数値的なバイアスがこのトレーニングの不正確さの根本原因です。
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 C++ の機械学習: C++ で一般的な機械学習アルゴリズムを実装するためのガイド
Jun 03, 2024 pm 07:33 PM
C++ の機械学習: C++ で一般的な機械学習アルゴリズムを実装するためのガイド
Jun 03, 2024 pm 07:33 PM
C++ では、機械学習アルゴリズムの実装には以下が含まれます。 線形回帰: 連続変数を予測するために使用されるステップには、データの読み込み、重みとバイアスの計算、パラメーターと予測の更新が含まれます。ロジスティック回帰: 離散変数の予測に使用されます。このプロセスは線形回帰に似ていますが、予測にシグモイド関数を使用します。サポート ベクター マシン: サポート ベクターの計算とラベルの予測を含む強力な分類および回帰アルゴリズム。
 機械学習における Golang テクノロジーの今後の動向の展望
May 08, 2024 am 10:15 AM
機械学習における Golang テクノロジーの今後の動向の展望
May 08, 2024 am 10:15 AM
機械学習の分野における Go 言語の応用可能性は次のとおりです。 同時実行性: 並列プログラミングをサポートし、機械学習タスクにおける計算量の多い操作に適しています。効率: ガベージ コレクターと言語機能により、大規模なデータ セットを処理する場合でもコードの効率が保証されます。使いやすさ: 構文が簡潔なので、機械学習アプリケーションの学習と作成が簡単です。




