方程式は二分木フォレストですか?未知の支配方程式や物理メカニズムをデータから直接発見
研究者は、機械学習手法を使用して、最も価値があり重要な固有法則を高次元の非線形データから直接自動的にマイニングし (つまり、問題の背後にある PDE ベースの支配方程式をマイニング)、自動知識発見を実現したいと考えています。
最近、東部工科大学、ワシントン大学、瑞来知能、北京大学の研究チームは、記号数学に基づく遺伝的アルゴリズム SGA-PDE を提案し、データからデータを抽出できるオープン候補セットを構築しました。 . 支配方程式の任意の形式を直接マイニングします。
実験によれば、SGA-PDE は Burgers 方程式 (相互作用項を含む)、Korteweg-de Vries 方程式 (KdV、高次微分項を含む)、および Chafee-Infante 方程式 (相互作用項を含む) をマイニングできるだけではありません。また、粘性重力流問題における複合関数を含む支配方程式と分数構造を含む方程式のマイニングにも成功しました。このうち後 2 つの方程式は、以前の方法では発見することが困難でした。 SGA-PDE は方程式形式に関する事前知識に依存せず、複雑な構造制御方程式マイニング問題のギャップを埋めます。このモデルは、方程式の候補セットを事前に与える必要がないため、未知の科学的問題における自動知識発見アルゴリズムの実際の適用に有益です。
この研究は「開形式偏微分方程式を発見するためのシンボリック遺伝的アルゴリズム (SGA-PDE)」と題され、6 月 1 日付けの Physical Review Research に掲載されました。

現在の共通知識発見のアイデアは、スパース回帰を使用することです。つまり、閉じた候補セットを事前に与え、そこから方程式項を選択し、支配方程式を結合します。 、SINDy や PDE-FIND など。ただし、このタイプの方法では、ユーザーが事前に方程式の大まかな形式を決定し、対応するすべての微分演算子を事前に候補セット内の関数項として提供する必要があります。 data の候補セットに存在します。最新の研究の一部では、遺伝的アルゴリズムを使用して候補セットを拡張しようとしていますが、遺伝子の組み換えや突然変異には大きな制限があり、依然として複雑な構造関数項 (分数構造や合成関数など) を生成することはできません。 オープン形式の支配方程式をデータから直接マイニングするための鍵は、計算しやすい方法で任意の形式の支配方程式を生成して表現し、どの程度適切であるかを測定することで方程式形式の精度を評価することです。生成された方程式は観察されたデータのプロパティに適合し、マイニングされた方程式を繰り返し最適化します。したがって、自動ナレッジ発見の中核となる問題は、表現と最適化です。
#表 1. 自動制御方程式マイニング手法の比較表
問題を表現する際の課題は次のとおりです:1 . 限られた基本単位を使用して無限の複雑な構造制御方程式 (つまり、オープン候補セット) を表現する方法 ##;2. 計算が容易な制御方程式表現方法を構築する方法。
研究者らは、あらゆる構造の方程式を自由に表現できるよう、SGA-PDEの基本表現単位をオペランドと演算子に弱体化し、記号数学を通じて二分木を用いてオープン候補集合を構築した。最適化問題の課題は次のとおりです: 1. 方程式形式と方程式評価指標の間の勾配を計算するのは困難です ; 2. 未解決候補の実行可能領域set は無限であり、最適化プロセスでは探索と活用のバランスを効果的に取ることが困難です。オープン候補集合問題を効率的に最適化するために、研究者らはツリー構造用に特別に設計された遺伝的アルゴリズムを使用して、方程式の形で最適化を実現しました。
#図 1: 自動知識発見問題と SGA-PDE の概略図
研究者らはまず方程式の基本を洗練させました。アルゴリズムでは、表現単位は開形式偏微分方程式を表現するために使用され、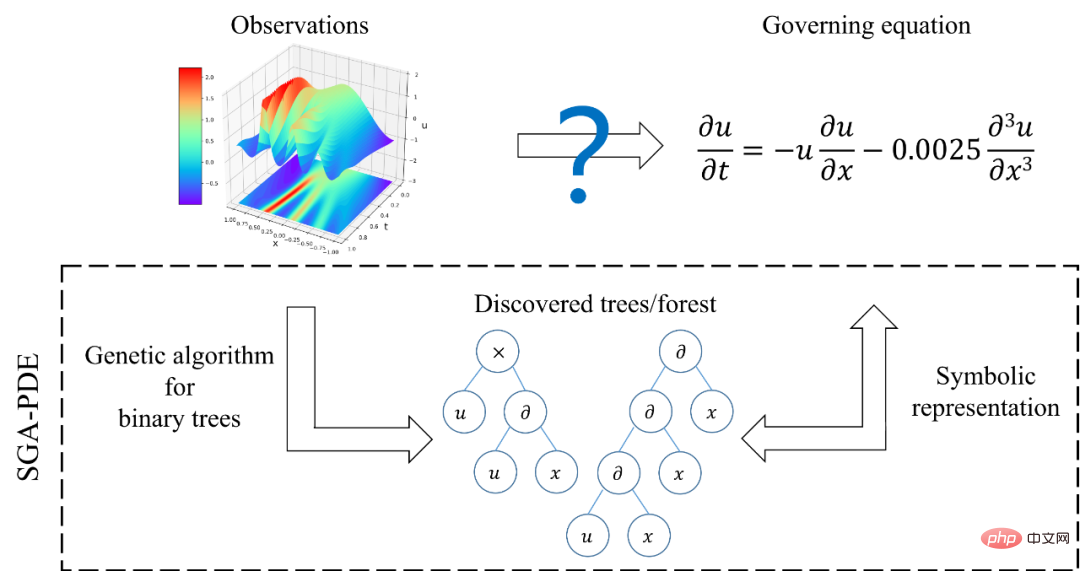 方程式の表現スケールを独立関数項のレベルから演算子とオペランドのより基本的なレベルに変換します。
方程式の表現スケールを独立関数項のレベルから演算子とオペランドのより基本的なレベルに変換します。
SGA-PDE は、制御方程式内の演算子を二重演算子 (- など) と単一演算子 (sin、cos など) に分割し、すべての潜在的な変数をオペランド (x、t、u など) として定義します。 。研究者は、バイナリ ツリーの構造を使用して演算子とオペランドを組み合わせ、さまざまな方程式をエンコードします。バイナリ ツリー内のすべての終端ノード (次数 0 の葉ノード) はオペランドに対応し、すべての非終端ノードは演算子に対応します。二重演算子は次数 2 のノードに対応し、単一演算子は次数 1 のノードに対応します。
図 2 に示すように、接続として計算可能な文字列を介して、任意の関数項を二分木に変換できますと同時に、 は特定の数学的規則を満たします。二分木は関数項に変換することもできます。さらに、複数の関数項を含む 支配方程式は、複数の二分木から構成されるフォレスト と等価です。 SGA-PDE は、記号数学を通じて任意の開形式偏微分支配方程式を表します。さらに、この論文では、数学的意味を持つ二分木をランダムに生成する方法も提案しています。これにより、生成された二分木が数学的原理に違反しないことが保証されます。
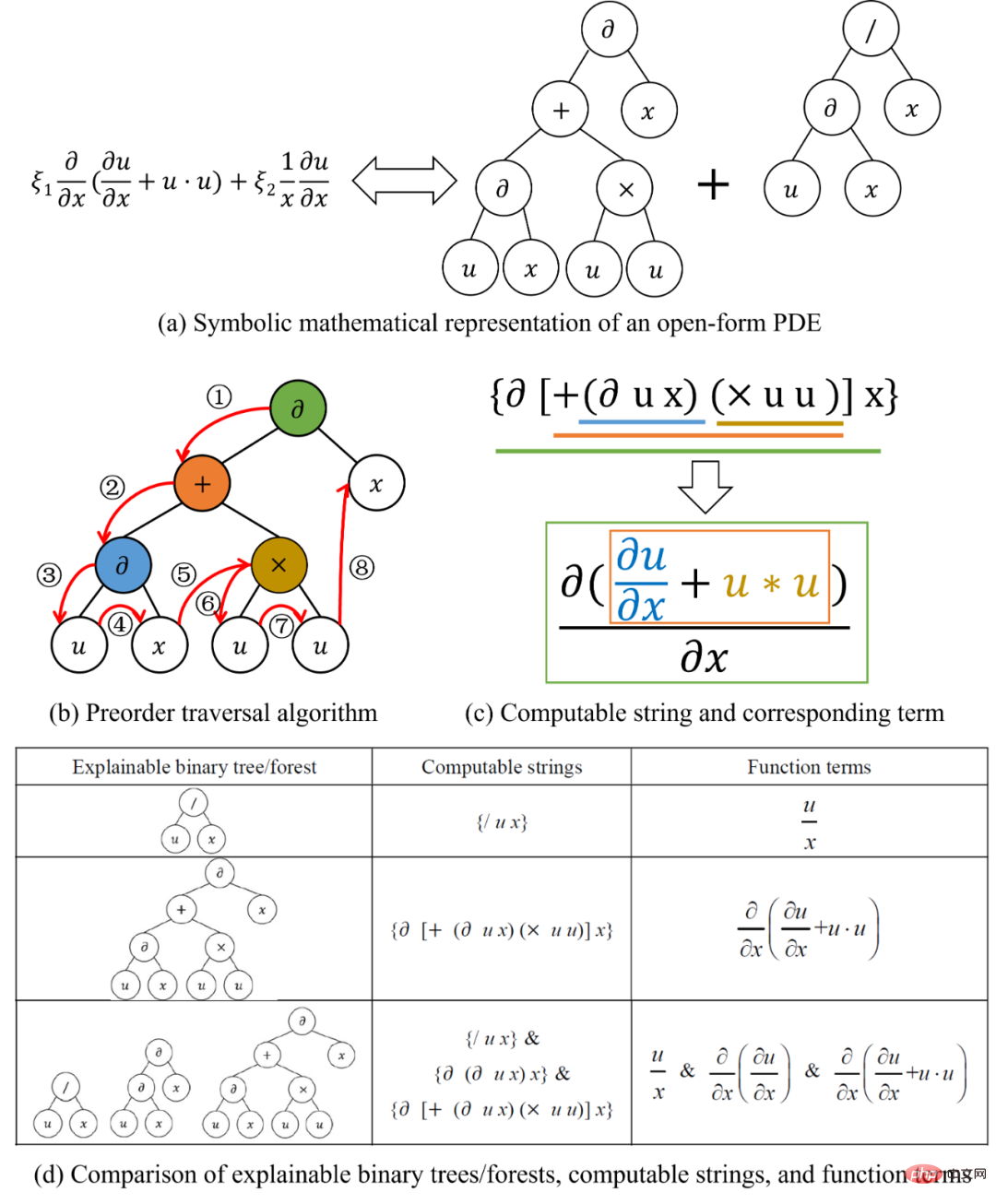
図 2: 二分木と関数項の間の表現と変換方法
図 2 に示す表現方法は次のとおりです。関数空間内のサンプルと二分木空間内のサンプル間の 1 対 1 の対応関係です。これは、記号数学に基づく表現方法が効率的かつ非冗長であり、遺伝的アルゴリズムの符号化プロセスとして使用できることを意味します。研究者らは、実験データから観測データと一致する制御方程式を自動的にマイニングするためのツリー構造の遺伝的アルゴリズム (図 3) を提案しました。ツリー構造用のこの遺伝的アルゴリズムは、さまざまなレベルでの最適化を実現できます。
再編成リンクは、フォレスト (方程式) レベルでを最適化し、バイナリ ツリー (関数項) の最適な組み合わせを見つけることです。このリンクは、閉じた候補セット内での最適化である、現在の一般的なスパース回帰手法に似ています。
突然変異リンクはバイナリ ツリー (関数項) レベルで最適化されます. 異なるノード属性をランダムに生成することにより、特定のバイナリ ツリー構造の下でノード属性の最適な組み合わせが見つかります。それは現在の構造を悪用したものです。
置換プロセスはバイナリ ツリー (機能項目) レベルでも最適化されますただし、新しいバイナリ ツリー構造が生成されます。これはツリー構造の探索であり、完全なオープン候補セットの最適化。 SGA-PDE は、マルチレベルの最適化を通じてバイナリ ツリー トポロジの利用と探索を考慮に入れることができ、最適な方程式形式を効率的に見つけるのに役立ちます。
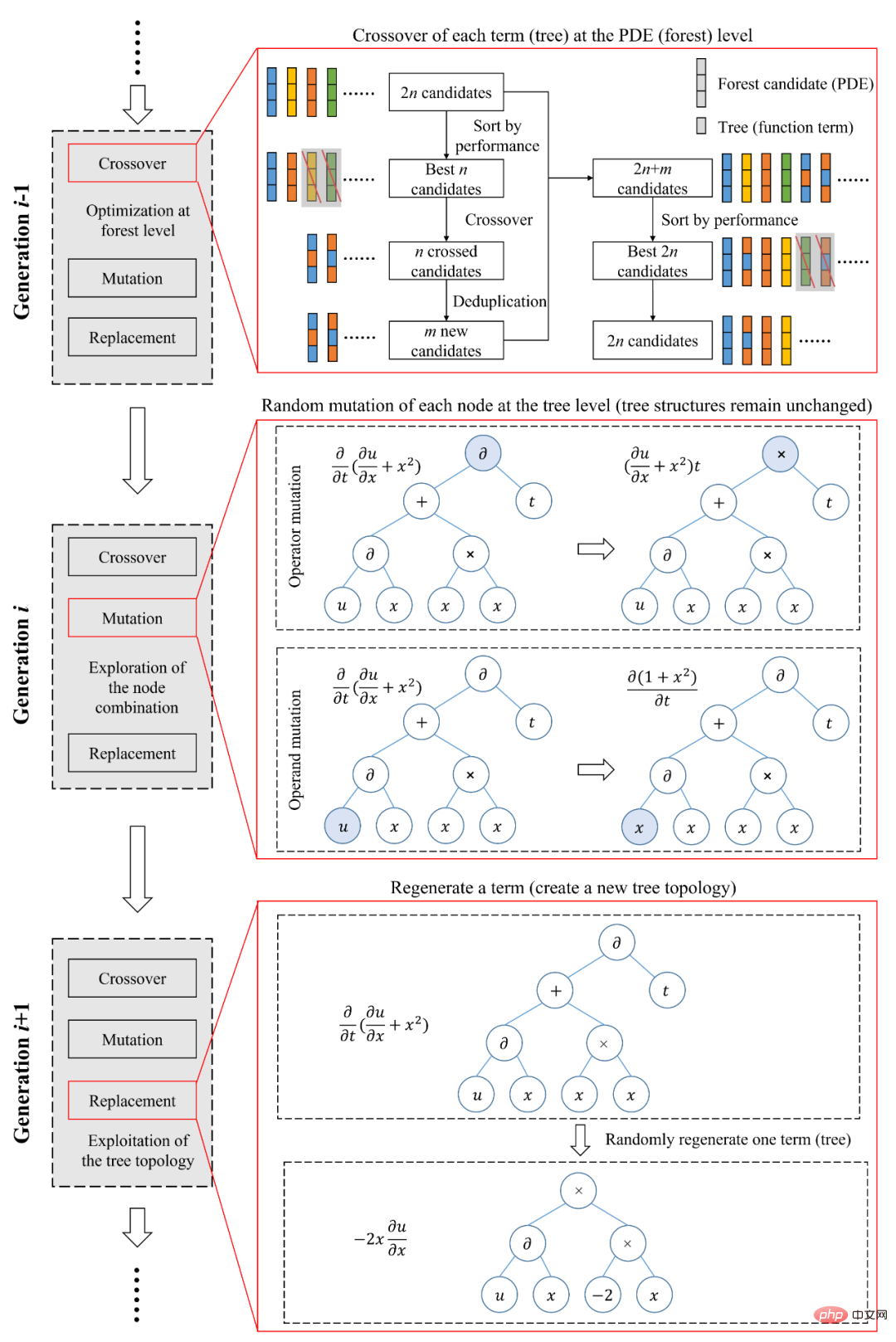 #図 3: ツリー構造の遺伝的アルゴリズム
#図 3: ツリー構造の遺伝的アルゴリズム
実験データを図 4 に示します。その 2 列目は次のとおりです。物理場の観測値 は、SGA-PDE の唯一の入力情報
です。列 3 と列 4 の基礎となる一次導関数は、物理場の観測値を差分することによって取得できます。列 1 は方程式の正しい形式です。実験では、SGA-PDE は同じプリセット オペランドと演算子を使用するため、アルゴリズムの多用途性を検証するために特定の問題に合わせて調整する必要はありません。最後に、SGA-PDE は、Burgers 方程式、KdV 方程式、Chafee-Infante 方程式、複合関数導出を伴う粘性重力流支配方程式、および分数構造を伴う方程式をデータからマイニングすることに成功しました。上の方程式には、指数項、高次微分項、交互作用項、複合関数、入れ子構造など、多くの複雑な形式が含まれています。 #表 2 は、上記 5 つの計算例における既存のさまざまなアルゴリズムの計算結果を比較したもので、複雑な構造の制御方程式のマイニングにおいて SGA-PDE がギャップを埋めることがわかります。
#図 4: 実験データのグラフ

#表 2 さまざまな制御方程式マイニング問題における自動知識発見アルゴリズムの実験結果
SGA の検索をより完全に理解するために、 PDE 最適化プロセス、図 5 は、KdV 方程式をマイニングする際の進化の経路を示しています。第一世代によって生成された最適な方程式は、実際の方程式からかけ離れていることがわかります。その後の進化の過程では、二分木の位相構造やノードの意味の変化、関数項間の交差組み換えなどを経て、第31世代でようやく正解が見出され、この時点でAIC 指数は、成形品基準で指定された収束に達しています。興味深いことに、最適化を継続すると、複合関数の導出に基づいた KdV 方程式のより節約的な式が世代 69 で見つかります。図 6 は、分数構造の支配方程式を見つけるための SGA-PDE の最適化プロセスを示しています。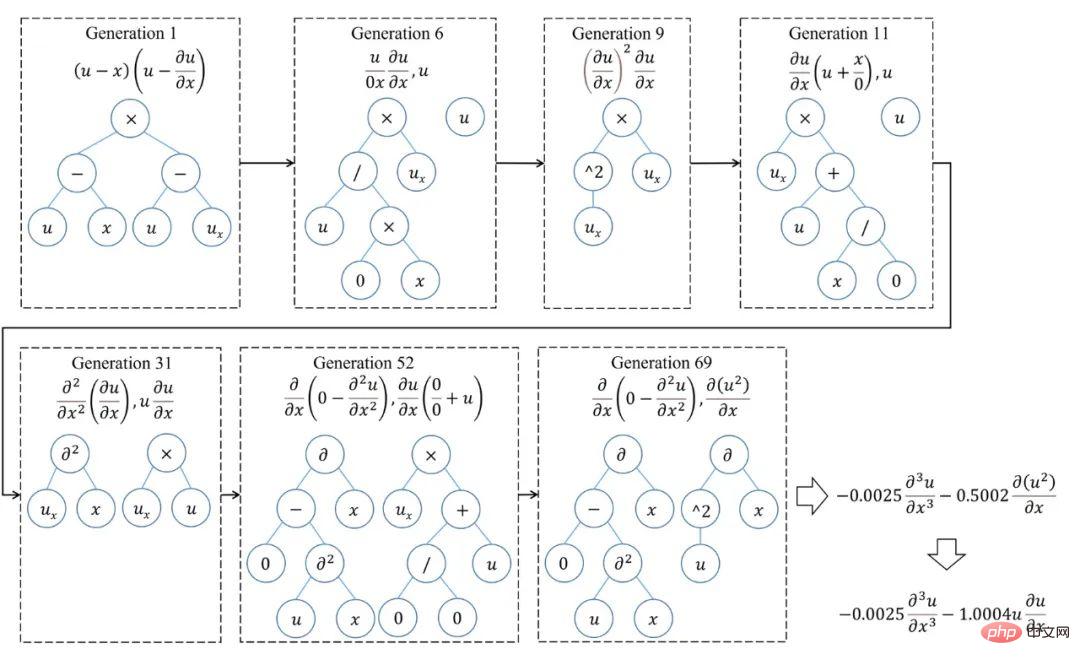
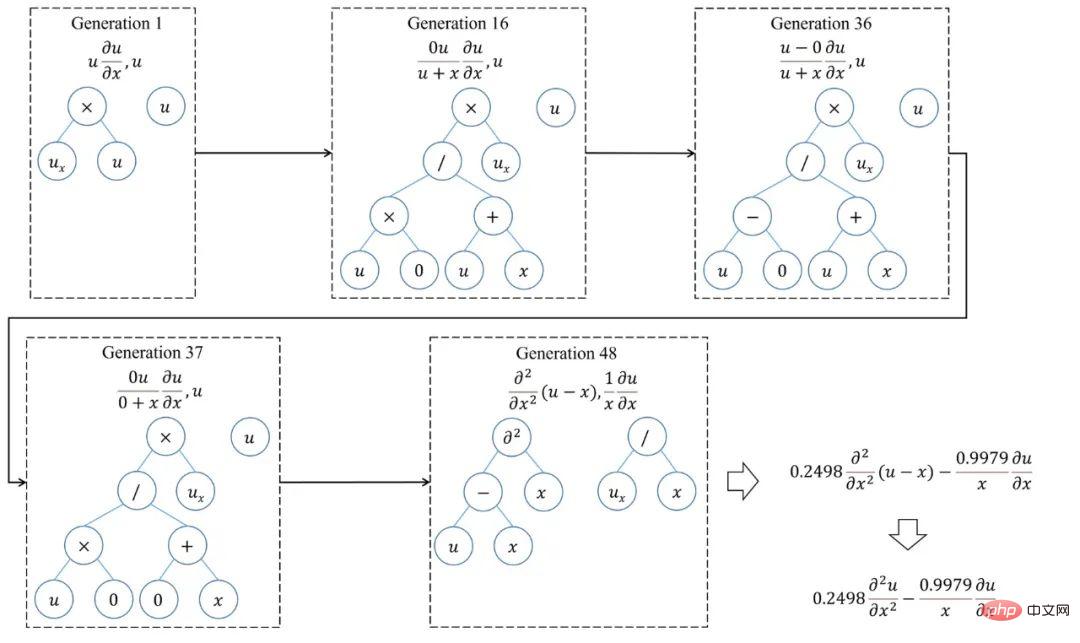 # #図 6: 分数構造の方程式の SGA-PDE 最適化プロセス
# #図 6: 分数構造の方程式の SGA-PDE 最適化プロセス
制御方程式はドメイン知識を効率的に表現しますが、現実世界の多くの問題では方程式パラメーターや方程式形式すら不確実です。正確な制御方程式を記述するのは難しく、機械学習におけるドメイン知識の適用が大幅に制限されます。
SGA-PDE は、記号数学を通じて方程式を変換し、任意形式の偏微分方程式の表現問題
を解決します。さらに、SGA-PDE はバイナリ ツリー用に設計された遺伝的アルゴリズムを使用し、ツリーのトポロジとノード属性の反復最適化を通じて、オープン ドメインからの観測データと一致する制御方程式を自動的にマイニングします。 SGA-PDE は、最適化において方程式の事前情報に依存せず、候補セットを与える必要もなく、複雑な構造方程式の 自動最適化を実現します。同時に、SGA-PDE は勾配のないアルゴリズムでもあり、方程式構造と損失値の間の勾配の難しい計算の問題を回避します。 今後の研究は次のことに焦点を当てます: 1. 強化学習または組み合わせ最適化アルゴリズムの組み合わせを試みる; 2. 物理メカニズムを埋め込むことで解空間を削減する; 3. 疎なデータと SGA-PDE の適用性を評価および改善するノイズの多いデータ、自然、4. 知識埋め込み手法と知識発見手法を統合します。 紙のリンク (無料で利用可能):
https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.023174
コードとサンプル データのリンク:
https://github.com/YuntianChen/SGA-PDE
以上が方程式は二分木フォレストですか?未知の支配方程式や物理メカニズムをデータから直接発見の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7486
7486
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 38
38
 ddrescue を使用して Linux 上のデータを回復する
Mar 20, 2024 pm 01:37 PM
ddrescue を使用して Linux 上のデータを回復する
Mar 20, 2024 pm 01:37 PM
DDREASE は、ハード ドライブ、SSD、RAM ディスク、CD、DVD、USB ストレージ デバイスなどのファイル デバイスまたはブロック デバイスからデータを回復するためのツールです。あるブロック デバイスから別のブロック デバイスにデータをコピーし、破損したデータ ブロックを残して正常なデータ ブロックのみを移動します。 ddreasue は、回復操作中に干渉を必要としないため、完全に自動化された強力な回復ツールです。さらに、ddasue マップ ファイルのおかげでいつでも停止および再開できます。 DDREASE のその他の主要な機能は次のとおりです。 リカバリされたデータは上書きされませんが、反復リカバリの場合にギャップが埋められます。ただし、ツールに明示的に指示されている場合は切り詰めることができます。複数のファイルまたはブロックから単一のファイルにデータを復元します
 オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
オープンソース!ゾーイデプスを超えて! DepthFM: 高速かつ正確な単眼深度推定!
Apr 03, 2024 pm 12:04 PM
0.この記事は何をするのですか?私たちは、多用途かつ高速な最先端の生成単眼深度推定モデルである DepthFM を提案します。従来の深度推定タスクに加えて、DepthFM は深度修復などの下流タスクでも最先端の機能を実証します。 DepthFM は効率的で、いくつかの推論ステップ内で深度マップを合成できます。この作品について一緒に読みましょう〜 1. 論文情報タイトル: DepthFM: FastMonocularDepthEstimationwithFlowMatching 著者: MingGui、JohannesS.Fischer、UlrichPrestel、PingchuanMa、Dmytr
 Excelのフィルター機能を複数条件で使う方法
Feb 26, 2024 am 10:19 AM
Excelのフィルター機能を複数条件で使う方法
Feb 26, 2024 am 10:19 AM
Excel で複数の条件によるフィルタリングを使用する方法を知る必要がある場合は、次のチュートリアルで、データを効果的にフィルタリングおよび並べ替えできるようにするための手順を説明します。 Excel のフィルタリング機能は非常に強力で、大量のデータから必要な情報を抽出するのに役立ちます。設定した条件でデータを絞り込み、条件に合致した部分のみを表示することができ、データ管理を効率化できます。フィルター機能を利用すると、目的のデータを素早く見つけることができ、データの検索や整理の時間を節約できます。この機能は、単純なデータ リストに適用できるだけでなく、複数の条件に基づいてフィルタリングすることもできるため、必要な情報をより正確に見つけることができます。全体として、Excel のフィルタリング機能は非常に実用的です。
 Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google が推進する JAX のパフォーマンスは、最近のベンチマーク テストで Pytorch や TensorFlow のパフォーマンスを上回り、7 つの指標で 1 位にランクされました。また、テストは最高の JAX パフォーマンスを備えた TPU では行われませんでした。ただし、開発者の間では、依然として Tensorflow よりも Pytorch の方が人気があります。しかし、将来的には、おそらくより大規模なモデルが JAX プラットフォームに基づいてトレーニングされ、実行されるようになるでしょう。モデル 最近、Keras チームは、ネイティブ PyTorch 実装を使用して 3 つのバックエンド (TensorFlow、JAX、PyTorch) をベンチマークし、TensorFlow を使用して Keras2 をベンチマークしました。まず、主流のセットを選択します
 iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhoneのセルラーデータインターネット速度が遅い:修正
May 03, 2024 pm 09:01 PM
iPhone のモバイル データ接続に遅延や遅い問題が発生していませんか?通常、携帯電話の携帯インターネットの強度は、地域、携帯ネットワークの種類、ローミングの種類などのいくつかの要因によって異なります。より高速で信頼性の高いセルラー インターネット接続を実現するためにできることがいくつかあります。解決策 1 – iPhone を強制的に再起動する 場合によっては、デバイスを強制的に再起動すると、携帯電話接続を含む多くの機能がリセットされるだけです。ステップ 1 – 音量を上げるキーを 1 回押して放します。次に、音量小キーを押して、もう一度放します。ステップ 2 – プロセスの次の部分は、右側のボタンを押し続けることです。 iPhone の再起動が完了するまで待ちます。セルラーデータを有効にし、ネットワーク速度を確認します。もう一度確認してください 修正 2 – データ モードを変更する 5G はより優れたネットワーク速度を提供しますが、信号が弱い場合はより適切に機能します
 超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
超知性の生命力が覚醒する!しかし、自己更新 AI の登場により、母親はデータのボトルネックを心配する必要がなくなりました。
Apr 29, 2024 pm 06:55 PM
世界は狂ったように大きなモデルを構築していますが、インターネット上のデータだけではまったく不十分です。このトレーニング モデルは「ハンガー ゲーム」のようであり、世界中の AI 研究者は、データを貪欲に食べる人たちにどのように餌を与えるかを心配しています。この問題は、マルチモーダル タスクで特に顕著です。何もできなかった当時、中国人民大学学部のスタートアップチームは、独自の新しいモデルを使用して、中国で初めて「モデル生成データフィード自体」を実現しました。さらに、これは理解側と生成側の 2 つの側面からのアプローチであり、両方の側で高品質のマルチモーダルな新しいデータを生成し、モデル自体にデータのフィードバックを提供できます。モデルとは何ですか? Awaker 1.0 は、中関村フォーラムに登場したばかりの大型マルチモーダル モデルです。チームは誰ですか?ソフォンエンジン。人民大学ヒルハウス人工知能大学院の博士課程学生、ガオ・イージャオ氏によって設立されました。
 柔軟かつ高速な 5 本の指を備え、人間のタスクを自律的に完了する初のロボットが登場、大型モデルが仮想空間トレーニングをサポート
Mar 11, 2024 pm 12:10 PM
柔軟かつ高速な 5 本の指を備え、人間のタスクを自律的に完了する初のロボットが登場、大型モデルが仮想空間トレーニングをサポート
Mar 11, 2024 pm 12:10 PM
今週、OpenAI、Microsoft、Bezos、Nvidiaが投資するロボット企業FigureAIは、7億ドル近くの資金調達を受け、来年中に自立歩行できる人型ロボットを開発する計画であると発表した。そしてテスラのオプティマスプライムには繰り返し良い知らせが届いている。今年が人型ロボットが爆発的に普及する年になることを疑う人はいないだろう。カナダに拠点を置くロボット企業 SanctuaryAI は、最近新しい人型ロボット Phoenix をリリースしました。当局者らは、多くのタスクを人間と同じ速度で自律的に完了できると主張している。人間のスピードでタスクを自律的に完了できる世界初のロボットである Pheonix は、各オブジェクトを優しくつかみ、動かし、左右にエレガントに配置することができます。自律的に物体を識別できる
 アメリカ空軍が初のAI戦闘機を公開し注目を集める!大臣はプロセス全体を通じて干渉することなく個人的にテストを実施し、10万行のコードが21回にわたってテストされました。
May 07, 2024 pm 05:00 PM
アメリカ空軍が初のAI戦闘機を公開し注目を集める!大臣はプロセス全体を通じて干渉することなく個人的にテストを実施し、10万行のコードが21回にわたってテストされました。
May 07, 2024 pm 05:00 PM
最近、軍事界は、米軍戦闘機が AI を使用して完全自動空戦を完了できるようになったというニュースに圧倒されました。そう、つい最近、米軍のAI戦闘機が初めて公開され、その謎が明らかになりました。この戦闘機の正式名称は可変安定性飛行シミュレーター試験機(VISTA)で、アメリカ空軍長官が自ら飛行させ、一対一の空戦をシミュレートした。 5 月 2 日、フランク ケンダル米国空軍長官は X-62AVISTA でエドワーズ空軍基地を離陸しました。1 時間の飛行中、すべての飛行動作が AI によって自律的に完了されたことに注目してください。ケンダル氏は「過去数十年にわたり、私たちは自律型空対空戦闘の無限の可能性について考えてきたが、それは常に手の届かないものだと思われてきた」と語った。しかし今では、




