最新の PNAS 研究: 81% の問題解決率、ニューラル ネットワーク Codex が高度な数学の世界への扉を開く

最近、新しい研究が PNAS に発表され、ニューラル ネットワークの機能が再び更新されました。今回は、ニューラル ネットワークを使用して高度な数学の問題を解決しました。それは、MIT 数学コースの難しい数学の問題でした。

この新しい研究で、研究チームは、OpenAI の Codex モデルがプログラム合成を実行して大規模な数学的問題を解決でき、小規模なサンプル学習を通じてデータセットの 81% を自動的に解決できることを証明しました。数学コースの問題で、Codex はこれらのタスクで人間レベルのパフォーマンスを達成しました。

元のリンク: https://www.pnas.org/doi/10.1073/pnas.2123433119

この研究の出現は、ニューラル ネットワークでは高度な数学の問題を解決できないという共通認識を覆します。研究チームは、「Codexがこのような機能を実現できるのは、まさにチームが大きな革新を行ったからだ。過去の失敗した研究ではテキストベースの事前学習のみが使用されており、今回登場したCodexニューラルネットワークは使用されていなかった」と指摘した。事前トレーニングのみがテキストに基づいて行われ、コードも微調整されます。

調査した質問データセットは、MIT の 6 つの数学コースとコロンビア大学の 1 つの数学コースから選択され、MIT の一変量ミクロン積分、多変数微積分、微分方程式、確率と統計の入門、コンピュータ サイエンスのための線形代数と数学、コロンビア大学の COMS3251 計算線形代数。

同時に、研究チームは、数学的推論を評価するための最新の高度な数学問題ベンチマークである MATH を使用して、OpenAI Codex の機能をテストしました。MATH は 6 つの主要な数学セクションから抽出されました: ジュニア代数、代数、計数と確率、中級代数、数論、微積分からそれぞれ 15 問。

#キャプション: 研究で使用されたコースの質問データセットと MATH ベンチマーク

調査によると、Codex は問題データ セットと MATH データ セット内の 265 の問題を解決し、そのうち 213 は自動的に解決されました。

1

イノベーションはどこにありますか #Transformer のリリース後、Transformer に基づく言語モデルはさまざまな自然言語処理 (NLP) で使用されています。 ) タスクを含む ゼロショットおよび数ショットの言語タスクで大きな成功を収めました。ただし、Transformer はテキストでのみ事前トレーニングされているため、これらのモデルは基本的に数学的な問題を解決することができません (GPT-3 がその典型的な例です)。

その後、少数ショット学習と思考連鎖 (CoT) プロンプトにより、GPT-3 の数学的推論機能が向上しましたが、コードなしでも、小規模ショットでも学習と CoT ヒントでは、GPT-3 は大学レベルの数学の問題や MATH ベンチマークでは依然として無力です。

数学的問題を解決するための過去の研究は、比較的単純な数学レベルで一定の結果を達成した可能性があります。たとえば、MAWPS や Math23k など、協調トレーニングの出力に基づいて式ツリーを検証または予測する手法は、小学校レベルの数学の問題を 81% 以上の精度で解くことができますが、高校、オリンピックの数学、または大学レベルの問題を解くことはできません。数学の問題。コース。グラフ ニューラル ネットワーク (GNN) と組み合わせた共同トレーニングにより、算術式ツリーを予測することで、機械学習における大学レベルの問題を最大 95% の精度で解決できます。しかし、この作業も数値的な回答に限定されており、過剰適合が生じ、他のコースに一般化することはできませんでした。

この作品の

最大の革新点

の 1 つは、Codex などの Transformer モデルがテキスト上で事前トレーニングされるだけでなく、コード上でも事前トレーニングされることです。 -大規模な数学的問題を解決するプログラムを生成できるように調整されています。

研究チームは、テストに入力画像や証明を必要としない質問サンプルをデータセットからランダムに選択しました。その中で、テキストのみで事前トレーニングされた言語モデル (GPT-3 text-davinci-002) は、コース問題の 18% と MATH ベンチマーク問題の 25.5% のみを自動的に解決しました。

対照的に、ゼロショット学習と、テキストで事前トレーニングされ、コードで微調整されたニューラル ネットワークを使用して合成されたプログラム (OpenAI Codex code-davinci-002) は、71% を自動的に解決できます。もちろん、MATH ベンチマーク問題の 72.2% を占めています。

同じニューラル ネットワーク Codex と数ショット学習を使用すると、コースの問題の 81% と MATH ベンチマーク テストの問題の 81.1% を自動的に解決できます。ただし、残りのモデルでは自動的に解決できなかったコース問題の 19% と MATH ベンチマーク問題の 18.9% は、手動プロンプトによって最終的に解決されました。

小規模サンプル学習法の追加は、この研究の 2 番目の主要な革新 です。上の図からわかるように、ゼロショット学習で質問に答えることができない場合、(質問、コード) を使用して (ペア) に対してスモールショット学習を実行します。 1) OpenAI を使用します text-similarity-babbage-001 埋め込みエンジンはすべての質問を埋め込みます;

2) 埋め込まれたコサイン類似度を使用して、コースから最も類似した解決された質問を計算します未解決の質問;

3) 最も類似した問題とそれに対応するコードを、小さなサンプル問題の例として取り上げます。

#図: 4 つの方法の自動問題解決率の比較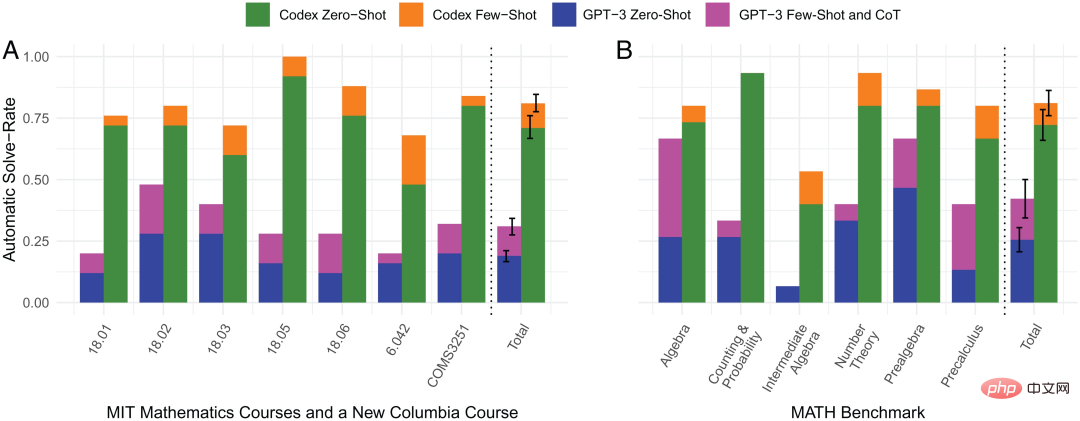

上の図は、Codex のゼロサンプル学習、小サンプル学習、GPT-3 のゼロサンプル学習、小サンプル学習の自動問題解決率の比較を示しています。図から、オレンジ色のバーで表される小規模サンプル学習 Codex は自動問題解決率に優れたパフォーマンスを示し、基本的にあらゆる数学分野で他の 3 つの方法よりもパフォーマンスが優れていることがわかります。

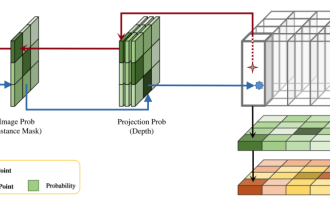
この研究の 3 番目の大きなイノベーションは、数学的問題を解決し、なぜその問題がそのように解決されるのかを説明するためのパイプラインを提供することです。下の図は MIT 5 の実行フローを示しています。数学コースでのパイプラインの説明。

18.01 の単一変数微積分問題を例にとると、問題と自動的に生成されたプレフィックス「Use SymPy」が与えられると、Codex はプロンプトを表示し、プログラムを出力します。プログラムを実行すると、正しい答えをもつ方程式が生成されます。その後、プログラムは再び Codex の入力を自動的に要求し、コードの説明が生成されます。

2

問題解決後

Codex は、数学の問題を解いて答えを説明するだけでなく、コースごとに新しい質問を生成するためにも使用されます。

生成された質問のレベルを評価するために、チームは、主に機械生成された質問の品質を比較するために、これらのコースまたは同じレベルのコースを受講した MIT の学生を対象にアンケートを実施しました。手書きの質問と難易度。

MIT の 6 つのコースのそれぞれでは、5 つの手書きの質問と 5 つのモデルで生成された質問が混合され、ランダムに提示されます。 60 の質問それぞれについて、参加学生は 3 つのアンケート質問に答えるように求められました。

1) この質問は人間が書いたものだと思いますか、それとも機械が作成したものだと思いますか?

2) この質問は特定のコースにとって適切だと思いますか、それとも不適切だと思いますか?

3 ) 1 (最も簡単) と 5 (最も難しい) のスケールで、この問題の難易度をどのように評価しますか?

返送されたアンケートでは、学生のアンケート結果は次のように要約されています。

• 機械で生成された質問と手動で書かれた質問の難しさは似ています。
• 人間が作成した質問は、機械が生成した質問よりもコースに適しています。
• 人間が書いた解答は誤答を特定するのが困難ですが、機械が生成した質問は、学生によって機械が生成したか人間が書いたかのいずれかであると考えられます。

#機械が生成した質問は学生には区別できなくなり、Codex が新しいコンテンツを作成する際に人間のパフォーマンス レベルに達したことを示しています。

ただし、モデルには解決できない問題もあります。たとえば、質問が画像やその他の非テキスト形式で表示されている場合は回答できません。解決策が必要な質問もあります。あるいは、非常に大きな素数の素因数分解などの計算困難な問題は、このモデルでは解決できません。ただし、この最後のタイプの質問は、実際の学生でも答えることができないため、数学の授業には出てくるべきではありません。

以上が最新の PNAS 研究: 81% の問題解決率、ニューラル ネットワーク Codex が高度な数学の世界への扉を開くの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。