最近人気のディフュージョンモデル、ディフュージョン世代モデルの初レビュー!

このレビュー (普及モデル: 手法とアプリケーションの包括的な調査) は、カリフォルニア大学の Ming-Hsuan Yang 氏と、北京大学 Cui Bin 研究所の Google Research によるものです。 、CMU、UCLA、モントリオール ミラ研究所およびその他の研究チームは、既存の拡散モデルの包括的な概要と分析を初めて実施し、拡散モデル アルゴリズムからの分類、他の 5 つの主要な生成モデルとの関連性、および拡散モデルのアルゴリズムによる分類を詳細に説明しました。 7 つの主要分野での応用を検討し、応用などを実施し、最終的に普及モデルの現状の限界と今後の発展の方向性を提案します。
記事リンク: https://arxiv.org/abs/2209.00796 拡散モデルの論文分類概要のこのレビュー github リンク: https://github.com/YangLing0818/ Diffusion -Models-Papers-Survey-Taxonomy
1
はじめにDiffusion モデルは、深い生成モデル SOTA の中で新しいものです。拡散モデルは、画像生成タスクにおいてオリジナルの SOTA: GAN を上回り、コンピュータ ビジョン、NLP、波形信号処理、マルチモーダル モデリング、分子グラフ モデリング、時系列モデリングなどの多くの応用分野で優れたパフォーマンスを発揮します。浄化など。さらに、拡散モデルは、ロバスト学習、表現学習、強化学習などの他の研究分野と密接に関連しています。
ただし、元の拡散モデルにも欠点があります。サンプリング速度が遅く、通常、サンプルを抽出するために数千の評価ステップが必要です。最尤推定は尤度ベースの推定と比較できません。他のモデルと比較すると、さまざまなデータ型に一般化する能力が劣ります。現在、多くの研究が実用化の観点から上記の制限を解決するため、または理論的な観点からモデルの機能を分析するために多くの努力が払われています。
しかし、アルゴリズムからアプリケーションに至る普及モデルの最近の進歩についての体系的なレビューは現在不足しています。この急速に成長する分野の進歩を反映するために、普及モデルの最初の包括的なレビューを紹介します。私たちは、私たちの研究が拡散モデルの設計上の考慮事項と高度な手法に光を当て、さまざまな分野での応用を実証し、将来の研究の方向性を示すことを構想しています。このレビューの概要を以下に示します。
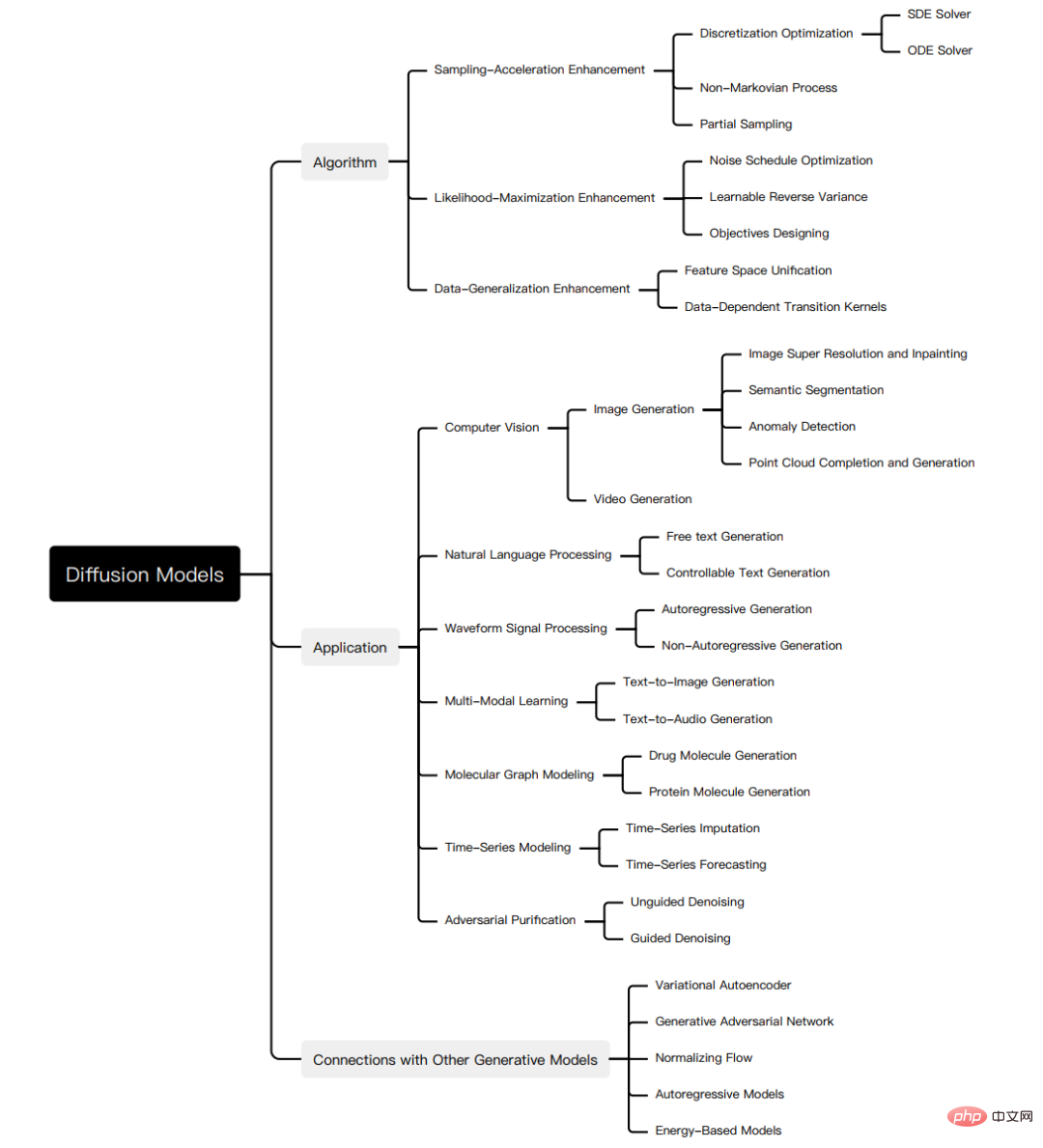
#拡散モデルはさまざまなタスクで優れたパフォーマンスを発揮しますが、依然として独自の欠点があり、多くの点が挙げられます。研究により拡散モデルが改善されました。
拡散モデルの研究の進捗状況を系統的に明らかにするために、元の拡散モデルの 3 つの主な欠点、つまりサンプリング速度の遅さ、最尤差、データの一般化の弱さをまとめました。また、拡散モデルの改善研究を、サンプリング速度の改善、最尤化の強化、およびデータ一般化の強化という 3 つの対応するカテゴリに分類することも提案されています。
最初に改善の動機を説明し、次に手法の特徴に応じて改善の方向ごとに研究を分類し、手法間の関連性と相違点を明確に示します。 。ここでは、例としていくつかの重要なメソッドのみを選択します。図に示すように、各タイプのメソッドは私たちの研究で詳しく紹介されています。 3 種類の拡散モデルを分析し、他の 5 つの生成モデル、GAN、VAE、自己回帰モデル、正規化フロー、エネルギーベース モデルを紹介します。
拡散モデルは多くの分野で優れた性能を発揮しており、拡散モデルは応用分野によって変形が異なることを考慮し、拡散モデルの応用研究を体系的に導入しました。 : コンピューター ビジョン、NLP、波形信号処理、マルチモーダル モデリング、分子グラフ モデリング、時系列モデリング、敵対的浄化。各タスクについて、タスクを定義し、拡散モデルを利用してタスクを処理する作業を紹介します。
この作業の主な貢献を次のように要約します。
- 新しい分類方法: 拡散モデルとその応用のための新しい体系的な分類方法を提案します。具体的には、モデルをサンプリング速度の強化、最尤推定の強化、データ一般化の強化の 3 つのカテゴリに分類します。さらに、拡散モデルのアプリケーションを、コンピューター ビジョン、NLP、波形信号処理、マルチモーダル モデリング、分子グラフ モデリング、時系列モデリング、および敵対的浄化の 7 つのカテゴリに分類します。
- 包括的なレビュー: 最新の普及モデルとその応用について、初めて包括的な概要を提供します。各普及モデルの主な改良点を示し、元のモデルと必要な比較を行い、対応する論文を要約します。普及モデルの適用の種類ごとに、普及モデルが対処する主な問題を提示し、それらの問題をどのように解決するかを説明します。
- 今後の研究の方向性: 私たちは将来の研究に対する未解決の質問を提起し、アルゴリズムとアプリケーションにおける拡散モデルの将来の開発についていくつかの提案を提供します。
2 拡散モデルの基礎
生成モデリングにおける中心的な問題は、モデルの柔軟性と計算能力のトレードオフのバランスです。拡散モデルの基本的な考え方は、順拡散プロセスを通じてデータの分布を体系的に撹乱し、その後、逆拡散プロセスを学習することでデータの分布を復元することで、非常に柔軟で計算が容易なモデルを生成することです。生成モデル。
(1) ノイズ除去拡散確率モデル (DDPM)
DDPM は、2 つのパラメータ化されたマルコフ連鎖構成と変分推論を使用して、有限時間後の元のデータ分布と一致するサンプルを生成します。フォワード チェーンの機能はデータに摂動を与えることであり、データの分布が事前分布、つまり標準ガウス分布になるまで、事前に設計されたノイズ スケジュールに従ってデータにガウス ノイズを徐々に追加します。逆方向チェーンは、指定された事前確率から開始され、パラメーター化されたガウス変換カーネルを使用して、元のデータ分布を徐々に復元することを学習します。が元のデータとその分布を表す場合、前方チェーンの分布は次の式で表すことができます。
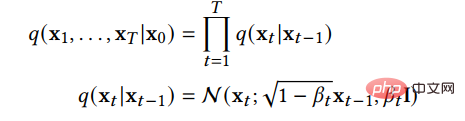
これは、前方チェーンがはマルコフプロセスとは、t段階のノイズを加えた後のサンプルであり、あらかじめ与えられたノイズの進み具合を制御するパラメータです。が 1 に近づくと、ほぼ標準ガウス分布に従うと考えられます。それが非常に小さい場合、逆プロセスの転送カーネルは近似的にガウスであると考えることができます。
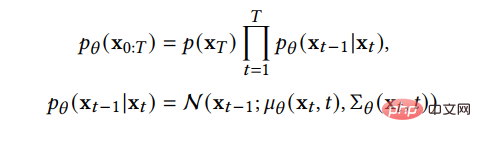
変分の下限は次のように学習できます。損失関数:
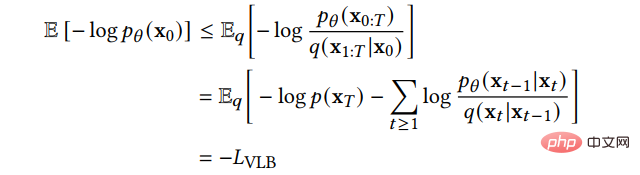
## (2) スコアベースの生成モデル (SGM)
上記の DDPM は、SGM の離散形式とみなすことができます。 SGM は、確率微分方程式(SDE)を構築してデータ分布を滑らかに乱し、元のデータ分布を既知の事前分布に変換します。対応する逆 SDE を使用して、以前の分布を元のデータ分布に変換します。
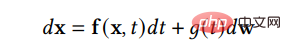
したがって、拡散プロセスを逆にしてデータを生成するには、必要な情報は、各時点における分数関数のみです。スコアマッチング手法を使用すると、次の損失関数を通じてスコア関数を学習できます:
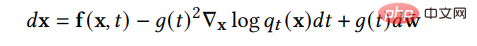
2 つの方法と 2 つの関係の詳細については、記事を参照してください。元の拡散モデルの 3 つの主な欠点は、サンプリング速度が遅い、尤度の最大化が不十分であること、およびデータ一般化能力が弱いことです。最近の研究の多くはこれらの欠点に対処しているため、改良された拡散モデルをサンプリング速度の強化、最尤化の強化、およびデータ一般化の強化の 3 つのカテゴリに分類します。次の 3、4、5 セクションで、これら 3 種類のモデルを詳しく紹介します。
3 サンプリング加速法
適用する場合、新しいサンプルの最高品質を達成するために、多くの場合、拡散モデルを処理する必要があります。数千回 新しいサンプルを取得するための 1 万ステップの計算。これにより、拡散モデルの実際の応用価値が制限されます。実際の応用では、多くの場合、処理の次のステップに材料を提供するために多数の新しいサンプルを生成する必要があるからです。
研究者は、拡散モデルのサンプリング速度を向上させるために多くの研究を行ってきました。これらの研究について詳しく説明します。これを、離散化最適化、非マルコフ プロセス、部分サンプリングの 3 つの方法に洗練します。
(1) 離散化最適化手法は、拡散 SDE を解く手法を最適化します。実際には複雑な SDE を解くには実解を近似するために離散解しか使用できないため、このタイプの方法では、サンプルの品質を確保しながら離散ステップの数を削減するために SDE の離散化方法を最適化しようとします。 SGM は、逆方向プロセスを解くための一般的な方法、つまり、順方向プロセスと逆方向プロセスに同じ離散化方法を採用する方法を提案します。順方向 SDE に離散化が与えられている場合:
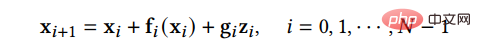
# 次に、逆 SDE も同じ方法で離散化できます:
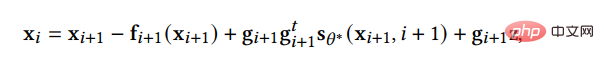
この方法は、単純な DDPM よりもわずかに優れています。さらに、SGM は SDE ソルバーに補正機能を追加し、各ステップで生成されるサンプルが正しい分布になるようにします。解法の各ステップで、ソルバーにサンプルが与えられた後、補正器はマルコフ連鎖モンテカルロ法を使用して、生成されたばかりのサンプルの分布を補正します。実験によると、ソルバーに補正器を追加すると、ソルバーのステップ数を直接増やすよりも効率的であることがわかりました。
(2) 非マルコフ過程メソッドは、元のマルコフ過程の制限を打ち破ります。逆プロセスの各ステップは、より多くの過去のサンプルに依存して新しいサンプルを予測できます。ステップ サイズを大きくすると、より適切な予測を行うこともできるため、サンプリング プロセスが高速化されます。その中で、主な作業である DDIM は、フォワード プロセスがマルコフ プロセスであることを前提とせず、次の分布に従います:
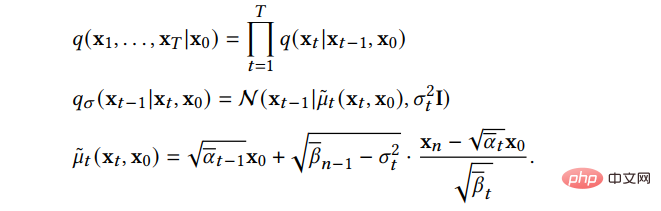
サンプリングDDIM のプロセスは離散化された正規微分方程式として扱うことができるため、サンプリング プロセスはより効率的であり、サンプルの内挿をサポートします。さらなる研究により、DDIM は多様体上拡散モデル PNDM の特殊なケースと見なすことができることがわかりました。
(3) 部分サンプリング法は、生成プロセスで時間ノードの一部を無視し、残りの時間ノードのみを使用してサンプルを生成することにより、サンプリング時間を直接短縮します。たとえば、漸進的蒸留は、トレーニングされた拡散モデルからより効率的な拡散モデルを蒸留します。トレーニングされた拡散モデルの場合、漸進的蒸留は新しい拡散モデルの 1 ステップがトレーニングされた拡散モデルの 2 ステップに対応するように拡散モデルを再トレーニングします。これにより、新しいモデルは古いモデルのサンプリング プロセスの半分を節約できます。具体的なアルゴリズムは次のとおりです。

この蒸留プロセスを継続的にループさせると、サンプリング ステップを大幅に削減できます。
4 最尤推定の強化
最尤推定における拡散モデルのパフォーマンスは、尤度関数に基づく生成モデルのパフォーマンスより劣りますが、最大画像圧縮、半教師あり学習、敵対的浄化など、多くのアプリケーション シナリオは非常に重要です。対数尤度を直接計算するのは難しいため、研究は主に変分下限 (VLB) の最適化と分析に焦点を当てています。拡散モデルの最尤推定を改善するモデルについて詳しく説明します。私たちはこれを、目標設計、ノイズ スケジュール最適化、学習可能な逆分散という 3 つのカテゴリの手法に細分化します。
(1) 目的 拡散 SDE を使用して、生成されたデータの対数尤度とスコア関数に一致する損失関数の関係を推定する設計手法です。このように、損失関数を適切に設計することで、VLB と対数尤度を最大化できます。 Song らは、プラグイン逆 SDE によって生成されたサンプルの尤度関数値が損失関数値以下になるように、損失関数の重み関数を設計できることを証明しました。尤度関数の上限。分数関数フィッティングの損失関数は次のとおりです。
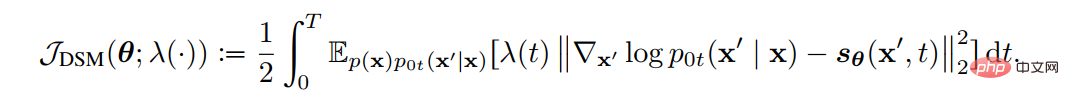
重み関数を拡散係数 g(t) に設定するだけで、次のようになります。損失関数は尤度関数の VLB、つまり
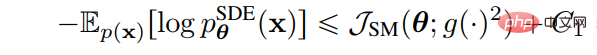
## (2) ノイズになります。設計に従って最適化をスケジュールするか、VLB を増やすためにフォワード プロセスのノイズの多い進行状況を学習します。 VDM は、離散ステップが無限大に近づくと、損失関数が信号対雑音比関数 SNR(t) の終点によって完全に決定されることを証明します。 # 次に、「離散ステップが無限大に近づくとき」では、信号対雑音比関数 SNR(t) のエンドポイントを学習することで VLB を最適化し、関数値を学習することでモデルの他の側面を改善できます。信号対雑音比関数の中央部分。 3. 学習可能な逆分散法は逆プロセスの分散を学習するため、フィッティング エラーが減少し、VLB を効果的に最大化できます。 Analytic-DPM は、DDPM と DDIM の逆プロセスに最適な期待値と分散があることを証明します。
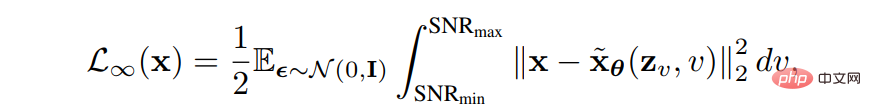
上記の式とトレーニング済みの Fractional を使用します。関数を使用すると、特定のフォワード プロセスの条件下で、最適な VLB をほぼ達成できます。
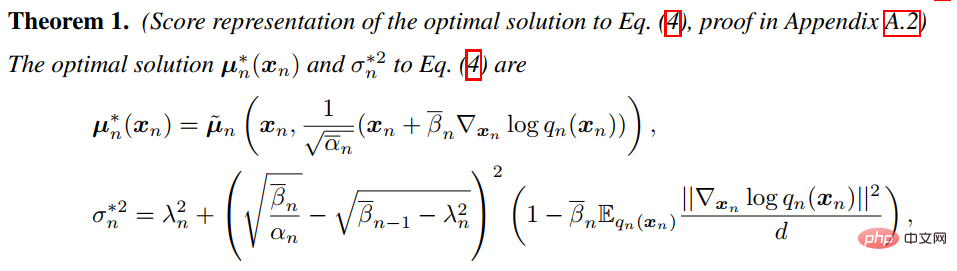 5
5
拡散モデルは、データがユークリッド空間、つまり平面幾何学を持つ多様体に存在すると仮定します。また、ガウス ノイズを追加すると必然的にデータが連続状態空間に変換されるため、拡散モデルは最初は写真などの連続データしか扱えず、離散データやその他のデータ型を直接適用する効果は乏しいです。これにより、普及モデルの適用シナリオが制限されます。
いくつかの研究成果は拡散モデルを他のデータ型に一般化しており、これらの方法について詳しく説明します。特徴空間統合とデータ依存遷移カーネルの 2 種類の手法に分類されます。
(1) 特徴空間統合法は、データを統合潜在空間に変換し、潜在空間上に拡散します。 LSGM は、VAE フレームワークを通じてデータを連続的な潜在空間に変換し、その上に拡散することを提案します。この方法の難しさは、VAE と拡散モデルを同時にトレーニングする方法です。 LSGM は、基礎となる事前分布が扱いにくいため、部分的なマッチング損失が適用されなくなることを示しています。 LSGM は、VAE の従来の損失関数 ELBO を損失関数として直接使用し、ELBO とスコア マッチングの関係を導き出します。
この式は定数を無視します。という意味で確立されています。拡散プロセスにおけるサンプルの分数関数をパラメータ化することにより、LSGM は ELBO を効率的に学習して最適化できます。
(2) データ依存型遷移カーネル法は、データ型の特性に応じて拡散過程における遷移カーネルを設計するため、拡散モデルを特定のデータ型に直接適用できます。 D3PM は、遅延ランダムウォーク、吸収状態などに設定できる離散データ用の遷移カーネルを設計しました。 GEODIFF は、3D 分子グラフ データ用の並進回転不変グラフ ニューラル ネットワークを設計し、不変初期分布と遷移カーネルによって不変周辺分布を導出できることを証明しました。これが次のような平行移動 - 回転変換であると仮定します。
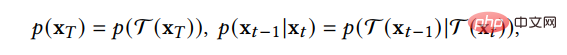
その場合、生成されたサンプル分布にも平行移動 - 回転の不変性があります。
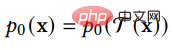
##6 他の生成モデルとの関係
以下の各セクションでは、最初に他の 5 つの重要なタイプの生成モデルを紹介します。そしてその強みと限界を分析します。次に、拡散モデルがそれらにどのように関連しているかを紹介し、拡散モデルを組み込むことでこれらの生成モデルをどのように改善できるかを説明します。 VAE、GAN、自己回帰モデル、正規化フロー、エネルギーベースのモデル、拡散モデルの関係を以下の図に示します。
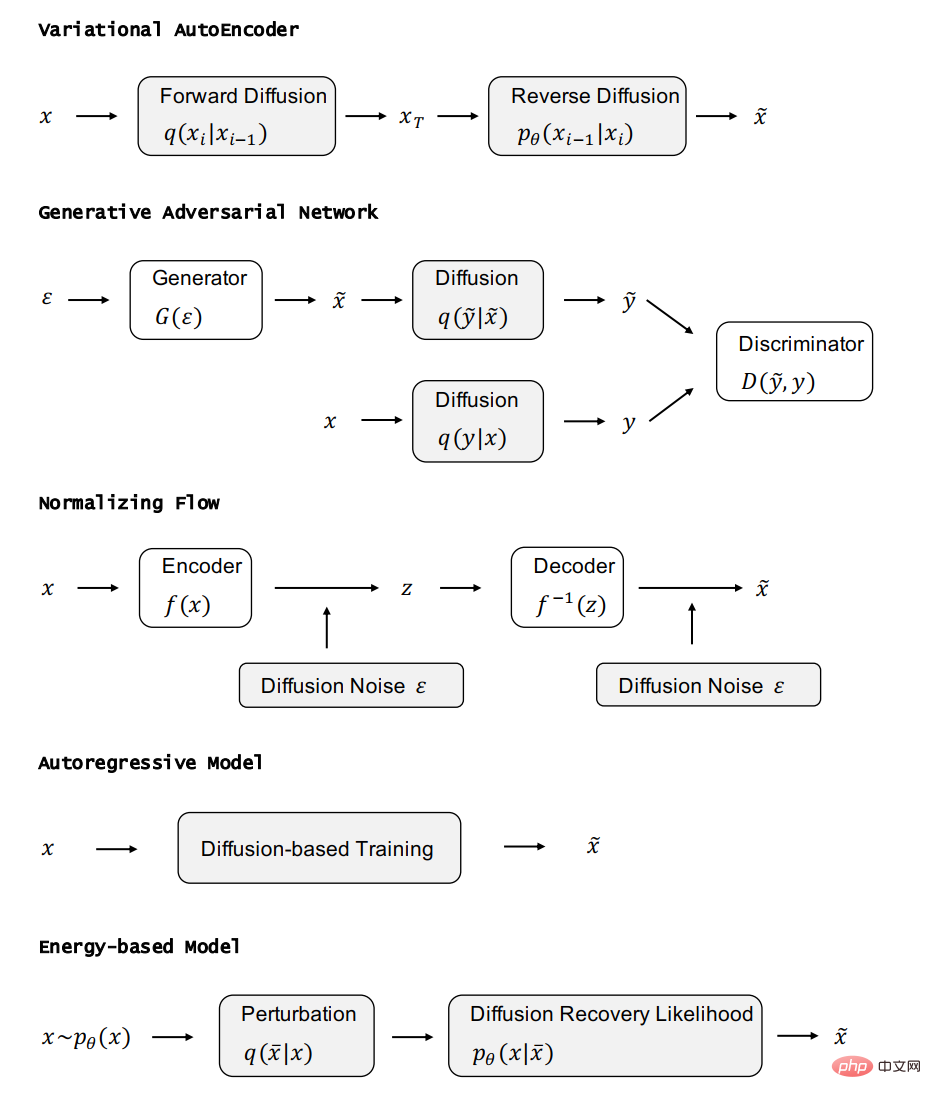
- ##DDPM は、階層的マルコフ VAE (階層的マルコフ VAE) とみなすことができます。ただし、DDPM と一般的な VAE の間には違いもあります。 VAE として、DDPM のエンコーダとデコーダは両方ともガウス分布に従い、マルコフ行を持ちます。隠れ変数の次元はデータ次元と同じです。デコーダのすべての層はニューラル ネットワークを共有します。
- DDPM は、GAN が不安定なトレーニングの問題を解決するのに役立ちます。データは高次元空間内の低次元多様体にあるため、GAN によって生成されたデータの分布は実際のデータの分布との重なりが低く、その結果、トレーニングが不安定になります。拡散モデルは体系的にノイズを追加するプロセスを提供します. 拡散モデルは生成されたデータと実際のデータにノイズを追加し, ノイズを追加したデータを識別器に送信します. これにより, GANがトレーニングできない問題や、トレーニングが不安定です。
- 正規化フローは、全単射関数を使用してデータを事前分布に変換します。このアプローチでは、正規化フローの表現能力が制限され、アプリケーションの結果が低下します。アナロジー拡散モデルはエンコーダにノイズを付加することでNormalizing flowの表現力を高めることができますが、見方を変えると、拡散モデルをフォワード処理でも学習できるモデルに拡張するアプローチです。
- 自己回帰モデルでは、データが特定の構造を持っていることを保証する必要があるため、自己回帰モデルの設計とパラメーター化が非常に困難になります。拡散モデルのトレーニングは、特定のトレーニング方法を通じて設計上の困難を回避する自己回帰モデルのトレーニングに影響を与えました。
- エネルギーベースのモデルは元のデータの分布を直接モデル化しますが、直接モデリングすると学習とサンプリングが困難になります。拡散回復尤度を使用することにより、モデルは最初にサンプルにわずかなノイズを追加し、次にわずかにノイズのあるサンプル分布から元のサンプルの分布を推測することができるため、学習とサンプリングのプロセスがよりシンプルかつ安定になります。
拡散モデルの応用
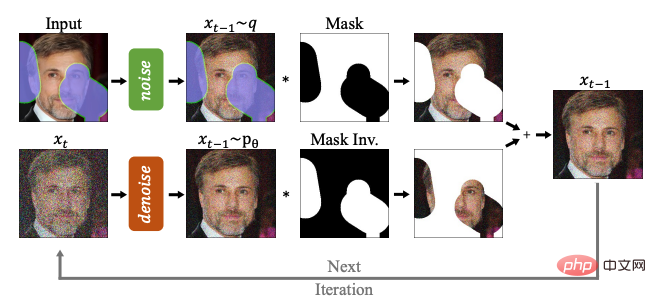
このセクションでは、コンピューター ビジョンと自然言語処理における拡散モデルの応用について紹介します。 、波形信号処理、マルチモーダル学習、分子グラフ生成、時系列および敵対的学習など、7 つの主要な応用方向のアプリケーションと、それぞれの種類のアプリケーションにおける手法を細分化して分析します。たとえば、コンピュータ ビジョンでは、拡散モデルを画像の完成と修復 (再ペイント) に使用できます。

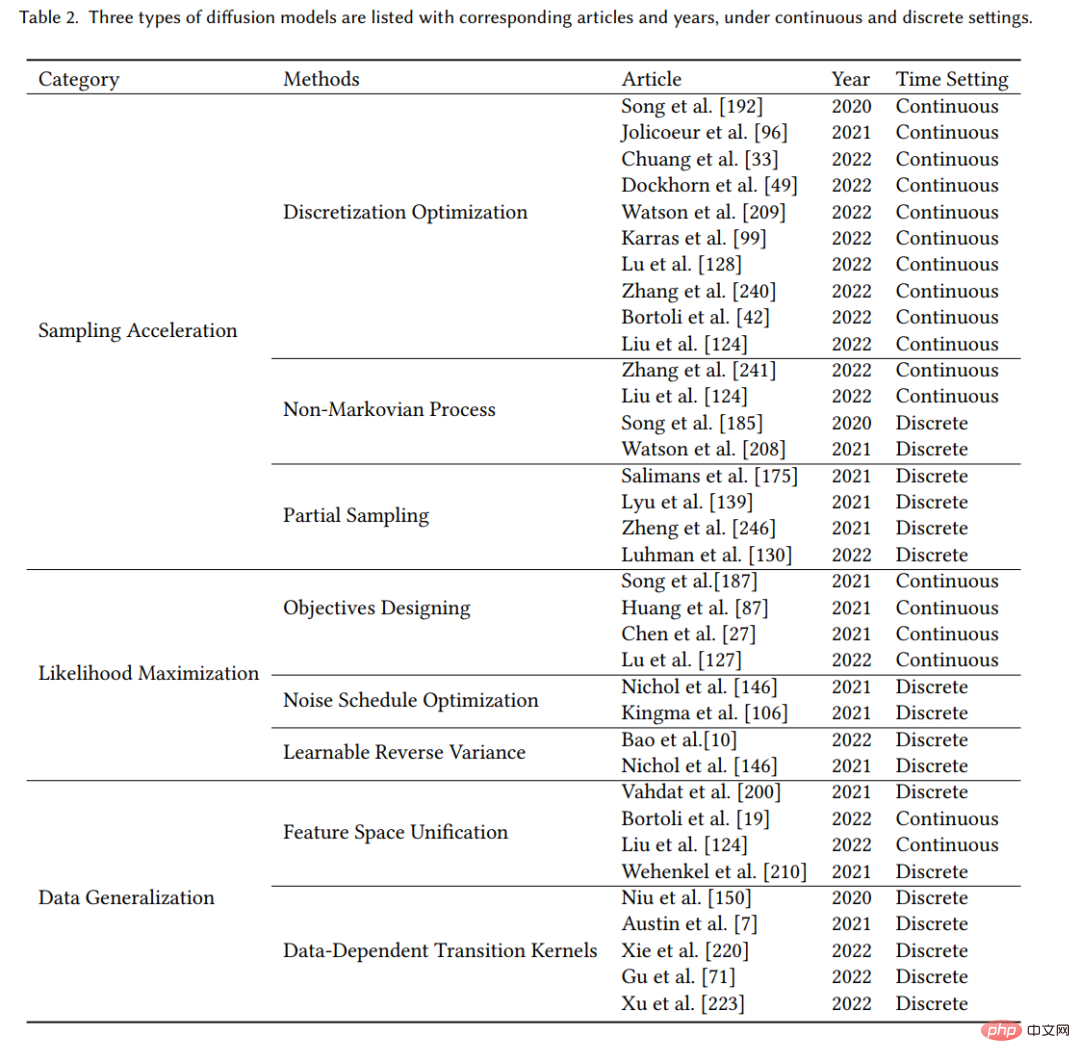
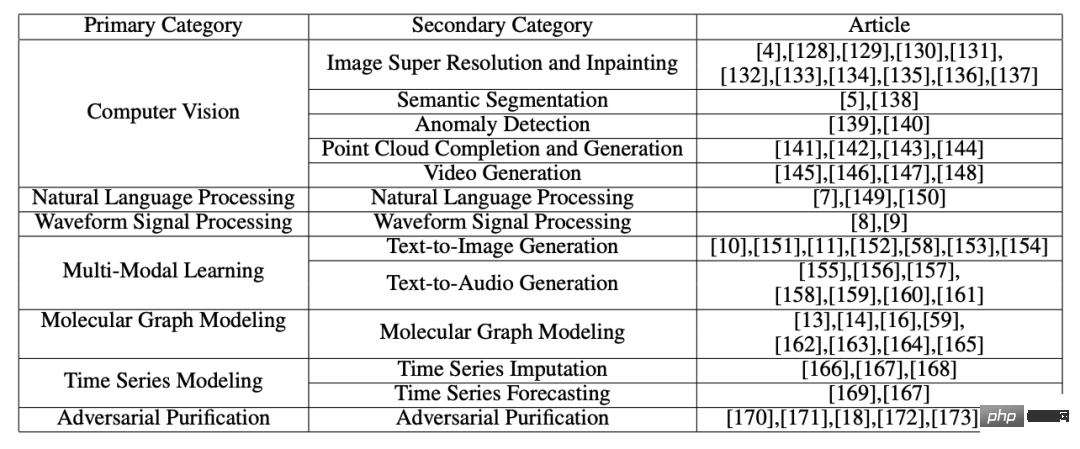
#アプリケーション分類の概要を表に示します。 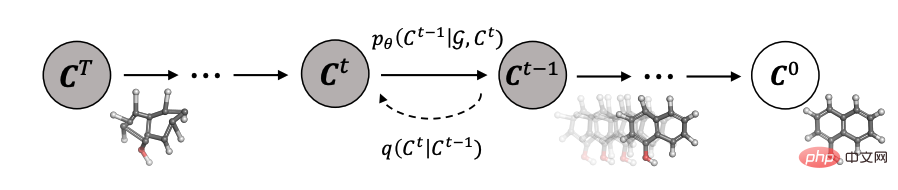
##8 今後の研究の方向性
以上が最近人気のディフュージョンモデル、ディフュージョン世代モデルの初レビュー!の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7487
7487
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 39
39
 世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
従来のコンピューティングを超える能力を備えているだけでなく、より低コストでより効率的なパフォーマンスを実現する人工知能モデルを想像してみてください。これは SF ではありません。世界で最も強力なオープンソース MoE モデルである DeepSeek-V2[1] が登場しました。 DeepSeek-V2 は、経済的なトレーニングと効率的な推論の特徴を備えた強力な専門家混合 (MoE) 言語モデルです。これは 236B のパラメータで構成されており、そのうち 21B は各マーカーをアクティブにするために使用されます。 DeepSeek67B と比較して、DeepSeek-V2 はパフォーマンスが優れていると同時に、トレーニング コストを 42.5% 節約し、KV キャッシュを 93.3% 削減し、最大生成スループットを 5.76 倍に高めます。 DeepSeek は一般的な人工知能を研究する会社です
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas は正式に電動ロボットの時代に突入します!昨日、油圧式アトラスが歴史の舞台から「涙ながらに」撤退したばかりですが、今日、ボストン・ダイナミクスは電動式アトラスが稼働することを発表しました。ボストン・ダイナミクス社は商用人型ロボットの分野でテスラ社と競争する決意を持っているようだ。新しいビデオが公開されてから、わずか 10 時間ですでに 100 万人以上が視聴しました。古い人が去り、新しい役割が現れるのは歴史的な必然です。今年が人型ロボットの爆発的な年であることは間違いありません。ネットユーザーは「ロボットの進歩により、今年の開会式は人間のように見え、人間よりもはるかに自由度が高い。しかし、これは本当にホラー映画ではないのか?」とコメントした。ビデオの冒頭では、アトラスは仰向けに見えるように地面に静かに横たわっています。次に続くのは驚くべきことです
 MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
今月初め、MIT やその他の機関の研究者らは、MLP に代わる非常に有望な代替案である KAN を提案しました。 KAN は、精度と解釈可能性の点で MLP よりも優れています。また、非常に少数のパラメーターを使用して、多数のパラメーターを使用して実行する MLP よりも優れたパフォーマンスを発揮できます。たとえば、著者らは、KAN を使用して、より小規模なネットワークと高度な自動化で DeepMind の結果を再現したと述べています。具体的には、DeepMind の MLP には約 300,000 個のパラメーターがありますが、KAN には約 200 個のパラメーターしかありません。 KAN は、MLP が普遍近似定理に基づいているのに対し、KAN はコルモゴロフ-アーノルド表現定理に基づいているのと同様に、強力な数学的基礎を持っています。以下の図に示すように、KAN は
 Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google が推進する JAX のパフォーマンスは、最近のベンチマーク テストで Pytorch や TensorFlow のパフォーマンスを上回り、7 つの指標で 1 位にランクされました。また、テストは最高の JAX パフォーマンスを備えた TPU では行われませんでした。ただし、開発者の間では、依然として Tensorflow よりも Pytorch の方が人気があります。しかし、将来的には、おそらくより大規模なモデルが JAX プラットフォームに基づいてトレーニングされ、実行されるようになるでしょう。モデル 最近、Keras チームは、ネイティブ PyTorch 実装を使用して 3 つのバックエンド (TensorFlow、JAX、PyTorch) をベンチマークし、TensorFlow を使用して Keras2 をベンチマークしました。まず、主流のセットを選択します
 テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボット「オプティマス」の最新映像が公開され、すでに工場内で稼働可能となっている。通常の速度では、バッテリー(テスラの4680バッテリー)を次のように分類します:公式は、20倍の速度でどのように見えるかも公開しました - 小さな「ワークステーション」上で、ピッキング、ピッキング、ピッキング:今回は、それがリリースされたハイライトの1つビデオの内容は、オプティマスが工場内でこの作業を完全に自律的に行い、プロセス全体を通じて人間の介入なしに完了するというものです。そして、オプティマスの観点から見ると、自動エラー修正に重点を置いて、曲がったバッテリーを拾い上げたり配置したりすることもできます。オプティマスのハンドについては、NVIDIA の科学者ジム ファン氏が高く評価しました。オプティマスのハンドは、世界の 5 本指ロボットの 1 つです。最も器用。その手は触覚だけではありません
 FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
目標検出は自動運転システムにおいて比較的成熟した問題であり、その中でも歩行者検出は最も初期に導入されたアルゴリズムの 1 つです。ほとんどの論文では非常に包括的な研究が行われています。ただし、サラウンドビューに魚眼カメラを使用した距離認識については、あまり研究されていません。放射状の歪みが大きいため、標準のバウンディング ボックス表現を魚眼カメラに実装するのは困難です。上記の説明を軽減するために、拡張バウンディング ボックス、楕円、および一般的な多角形の設計を極/角度表現に探索し、これらの表現を分析するためのインスタンス セグメンテーション mIOU メトリックを定義します。提案された多角形モデルの FisheyeDetNet は、他のモデルよりも優れたパフォーマンスを示し、同時に自動運転用の Valeo 魚眼カメラ データセットで 49.5% の mAP を達成しました。
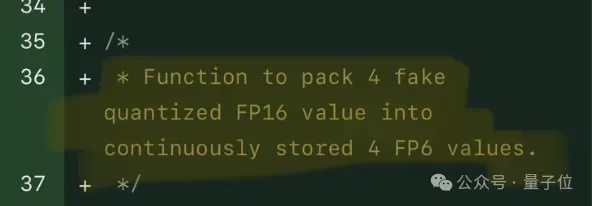 Llama 70B を実行するシングル カードはデュアル カードより高速、Microsoft は FP6 を A100 オープンソースに強制導入
Apr 29, 2024 pm 04:55 PM
Llama 70B を実行するシングル カードはデュアル カードより高速、Microsoft は FP6 を A100 オープンソースに強制導入
Apr 29, 2024 pm 04:55 PM
FP8 以下の浮動小数点数値化精度は、もはや H100 の「特許」ではありません。 Lao Huang は誰もが INT8/INT4 を使用できるようにしたいと考え、Microsoft DeepSpeed チームは NVIDIA からの公式サポートなしで A100 上で FP6 の実行を開始しました。テスト結果は、A100 での新しい方式 TC-FPx の FP6 量子化が INT4 に近いか、場合によってはそれよりも高速であり、後者よりも精度が高いことを示しています。これに加えて、エンドツーエンドの大規模モデルのサポートもあり、オープンソース化され、DeepSpeed などの深層学習推論フレームワークに統合されています。この結果は、大規模モデルの高速化にも即座に影響します。このフレームワークでは、シングル カードを使用して Llama を実行すると、スループットはデュアル カードのスループットの 2.65 倍になります。 1つ




