人間は、成長プロセスのさまざまな段階で多数の数学的問題を解決するために、多くの知識ポイントを習得する必要があります。しかし、知識の要点を理解しただけでは本当に理解したわけではなく、問題を解決できて初めて人間の知恵が反映されるのです。近年、ニューラル ネットワークはコンピュータ ビジョン、パターン マッチング、自然言語処理、強化学習などの分野で大きな成功を収めていますが、ニューラル ネットワーク モデルの離散的組み合わせ推論能力は人間のそれよりもはるかに低いです。では、ニューラル ネットワークは数学的問題を理解し、解決できるのでしょうか?もしそうなら、ニューラルネットワークの問題解決能力はどれほど優れているのでしょうか?
データ形式の観点から見ると、数学的問題はシーケンスとみなすことができ、その解決策 (問題解決の手順または式) は、シーケンスの形式で提示されることがよくあります。したがって、数学的問題を解くことは、自然言語から数学的言語への変換問題とみなすことができ、ニューラル ネットワーク モデルは数学的問題を形式的に解決することができます。これまでのさまざまな研究成果から、ニューラル ネットワークは翻訳問題で非常に優れたパフォーマンスを達成でき、複数のデータ セットで人間のパフォーマンスを超えていることが知られています。ただし、機械翻訳とは大きく異なります。数学的問題を解決するには、質問の意味を理解する能力に加えて、多くの場合、代数的な一般化されたオブジェクトとエンティティの離散的な組み合わせについて推論する能力がモデルに必要です。
数学的問題を解決するディープ モデルの能力を調査するために、中山大学人間機械知能統合研究室では、小学校および中学校の数学の応用問題と幾何学的な計算問題を使用しました。まず、深層モデルの意味理解、認知推論、数学的問題解決能力を向上させるために、一連の研究が実施されました。この記事では、中山大学人間・機械・物体知能統合研究室による数学的問題解決分野における一連の研究を簡単に紹介します。
論文 1: 数学文章題用の意味的に整合されたユニバーサル ツリー構造ソルバー
#The 2020 Conference on Empirical Methods in Natural Language Processing
##論文アドレス: https://aclanthology.org /2020.emnlp-main.309.pdf
#実用的な数学文章題ソルバーは、一次方程式などのさまざまな種類の数学文章題を解ける必要があります。変数、2変数1次方程式系、1変数2次方程式など。しかし、ほとんどの数学応用問題解決作業は四則演算のみを対象として設計されており、この種の設計をより多くの問題タイプに拡張するのは困難であることが多く、統合された数学応用問題ソルバーを使用してさまざまなタイプの式を解くことは不可能です。アプリケーションに関する質問も同時に行います。さらに、現在のほとんどの数学文章問題ソルバーには、問題テキストと解答式の間に意味上の制約がありません。
上記の問題に対応して、中山大学人間機械知能統合研究室チームは、統一された式ツリー表現スキームを提案しました。 -yuan 1 次方程式、2 変数の 1 次方程式、1 変数の 2 次方程式などの式を統一して表現できるため、ソルバーの設計が簡素化され、さまざまな種類のアプリケーション問題を解決できます。図1。
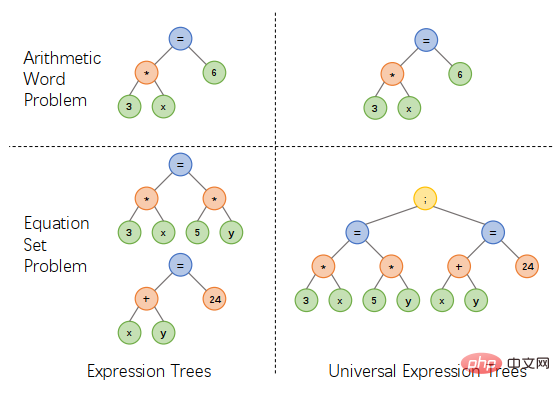
#図 1 統合された式ツリー表現スキームの設計
統一式ツリー表現スキームに基づいて、図 2 に示すように、意味的に整合されたツリー構造ユニバーサル ソルバー (SAU-Solver) をさらに提案します。当社のツリー構造ユニバーサル ソルバーは、2 層 GRU に基づく問題エンコーダーと、統一された式ツリー表現に基づくツリー構造デコーダーの 2 つの部分で構成されます。また、トレーニング プロセス中に、セマンティック アライメント正則化を導入しました。式のサブツリーと質問コンテキストの一貫性を制約することで、一般的なソルバーは問題と式の間の意味論的な関係をより完全に考慮し、さまざまなタイプの問題を調査できます。知識が得られるため、ソルバーの式生成機能が向上します。
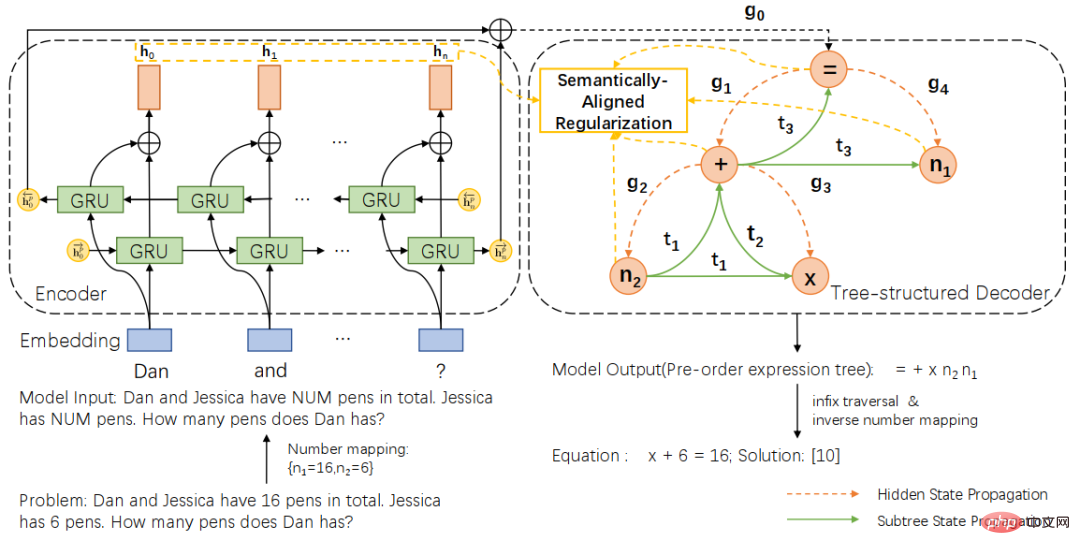
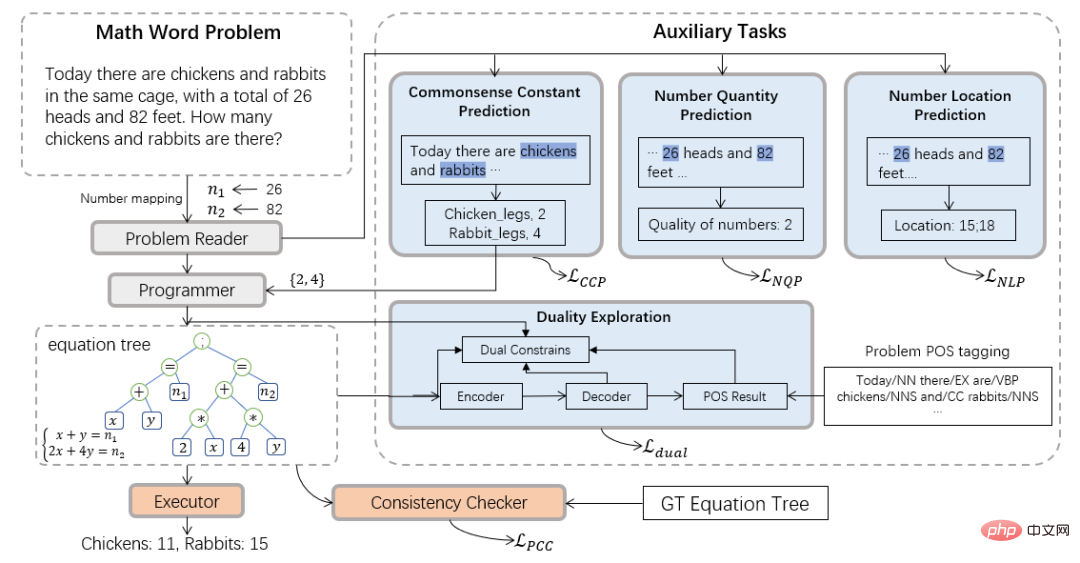
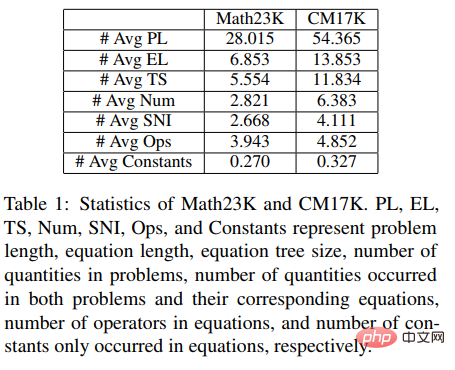
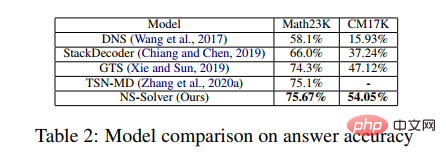
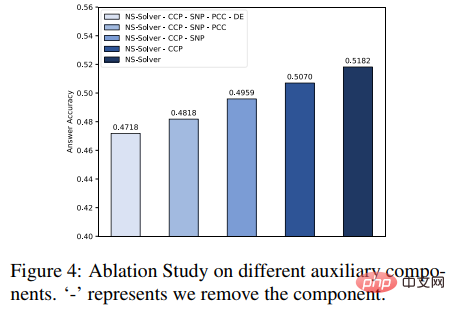
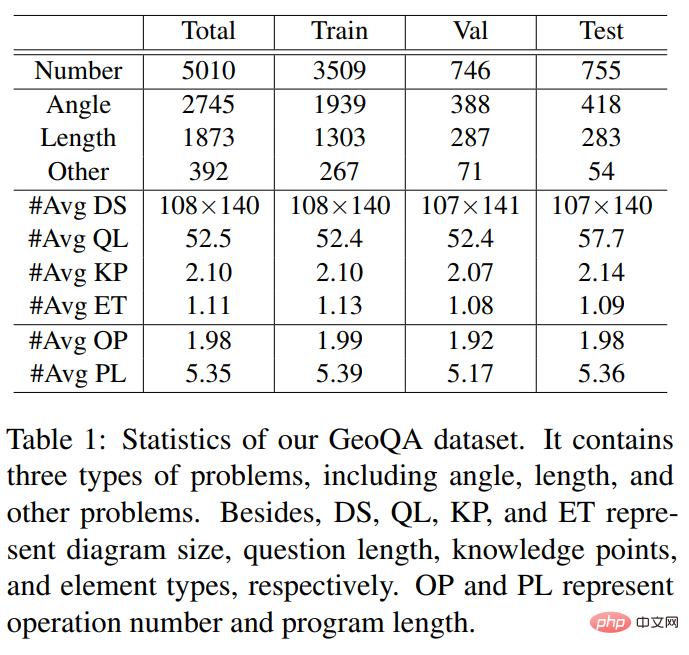
#図 2 セマンティック アラインメント ツリー構造ソルバー さらに、ソルバーの汎用性と解決能力をより適切に測定するために、現在のアノテーション データ セット内の単一タイプの質問を含む問題用の中規模の複数質問データ セット HMWP も構築しました。 . データ セットには、1 変数の線形方程式、2 変数の連立一次方程式、1 変数の 2 次方程式など、さまざまな式タイプを解く数千の数学テキストの質問が含まれています。私たちの実験は、複数の質問タイプを含むデータ セットは、単一タイプのデータ セットよりもソルバーにとってより困難であることを示しています。また、ソルバーの問題解決能力をより適切に測定し、ソルバー コミュニティでの研究を促進することもできます。 実験では、記事では提案された SAU ソルバーを HMWP、Math23K、ALG514、および Dolphin18K-Manual の既存の手法と比較しました。実験結果を下の図に示します。これは、私たちの方法の多用途性とより優れた数学的問題解決能力を証明しています。 研究の詳細については、元の論文を参照してください。 論文 2: 補助タスクを使用した数学文章問題のニューラルシンボリック ソルバー 計算言語学協会第 59 回年次総会および自然言語処理に関する第 11 回国際共同会議 論文アドレス: https://arxiv.org/abs/2107.01431 初等数学応用問題の現在のソルバーは、さまざまな数学記号の制約を考慮せず、単純な問題のみを解決します。エンコーダ/デコーダ フレームワークを不適切に使用し、不合理な予測につながります。記号的制約と記号的推論の導入は、数学的応用問題を自動的に解決するために非常に重要です。 そこで、中山大学人間機械知能統合研究所チームは、ニューロシンボリックコンピューティングパラダイムを導入し、次のことを支援する新しいニューロシンボリックソルバー(NS-Solver)を提案しました。タスク 明示的知識の注入を実行して、さまざまなレベルの記号制約を実現します。その技術アーキテクチャを図 3 に示します。 NS-Solver は、次の 3 つのコンポーネントによってネットワークのバックボーン上に構築されます: 1) 2 層の双方向 GRU ネットワークを通じて数学的問題の意味論的な理解と表現を効率的に実行するプロブレム リーダー、2) 記号推論に基づく記号推論を担当するプログラマー問題の意味論と常識的な予測結果に基づいて、解決式を生成します。 3) 実行者、sympy ライブラリを使用して式を解き、最終的な答えを取得します。 シンボル制約に関しては、追加のトレーニング信号と常識的な予測結果を使用してシンボル テーブルを明示的に制約し、問題解決の検索スペースを削減するためのさまざまな補助タスクを提案します。 1) 自己-教師付き数値予測タスク: 質問内の数値の位置と数を予測することで、質問のセマンティクスをよりよく理解します; 2) 常識的な量指定子予測タスク: 常識的な知識を注入し、予測結果を使用してシンボル テーブルを制約し、検索スペース; 3) 一貫性チェック: ソルバーの出力とターゲット式の間の一貫性を意味レベルからチェック; 4) 二重利用タスク: 問題から式への双方向制約を通じてソルバーの問題の意味理解を強化します。そして問題への表現。 図 3 ニューラルシンボリック ソルバー (NS ソルバー) さらに、ソルバーのパフォーマンスをより適切に検証するために、数学的問題解決コミュニティでの研究をより促進するために、より大規模な複数質問の数学的応用問題データ セット CM17K も構築しました。 CM17K には、4 変数の算術問題が 6,215 問、1 変数の線形方程式が 5,193 件、1 変数の非線形方程式が 3,129 件、方程式が 2,498 件含まれています。 CM17K と Math23K の統計を以下の表に示します。統計から、CM17K は Math23K よりも長い質問情報、より長い解法表現を持ち、より多くの常識を含んでいることがわかります。これは、CM17K が、解決の難易度という点で問題ソルバーのパフォーマンスをよりよく特徴づけていることを意味します。 実験では、記事は提案された NS-Solver を Math23K および CM17K の既存の手法と比較し、NS-Solver が優れた問題解決スキルを備えていることを証明するためにアブレーション実験を実施しました。そして多用途性。実験結果を次の 2 つの表に示します。 #さらに、下図に示すように、補助作業に関するアブレーション実験も実施しました。実験結果は、各補助タスクが NS-Solver の問題解決能力を向上させることができることを証明しています。 研究の詳細については、元の論文を参照してください。 論文 3: GeoQA – マルチモーダル数値推論に向けた幾何学的質問回答ベンチマーク 計算言語学協会の調査結果: ACL-IJCNLP 2021 論文アドレス: https://arxiv .org/pdf/2105.14517.pdf 自動数学的問題解決は、最近ますます注目を集めています。数学的問題の自動解決 ほとんどの研究は、数学的な文章題を自動的に解くことに重点を置いています。しかし、幾何学の問題に焦点を当てた作品はほとんどありません。数学の応用問題と比較して、幾何学の問題では、文章の説明と図表を同時に理解する必要があります。これは、幾何学問題では、問題文と図表が通常相互に補完し合い、不可欠であるためです。ジオメトリ問題を自動的に解決する既存の方法はルールに大きく依存しており、小規模なデータ セットでのみ評価されます。 #図 4 幾何学に関する質問の例
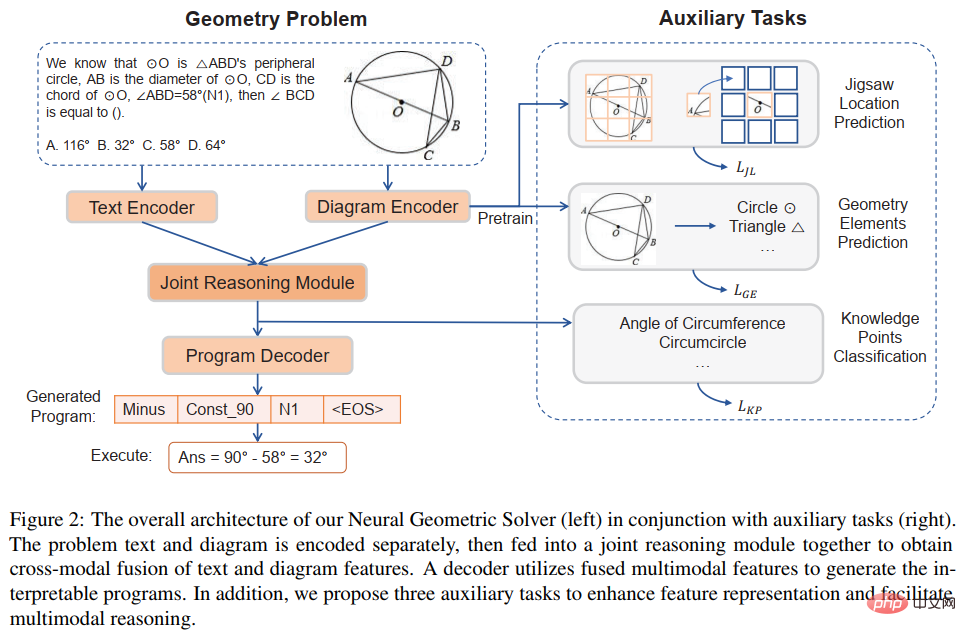
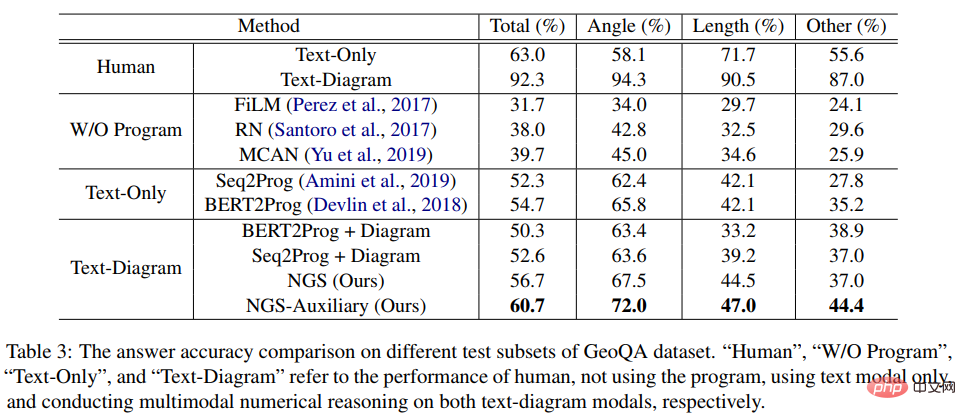
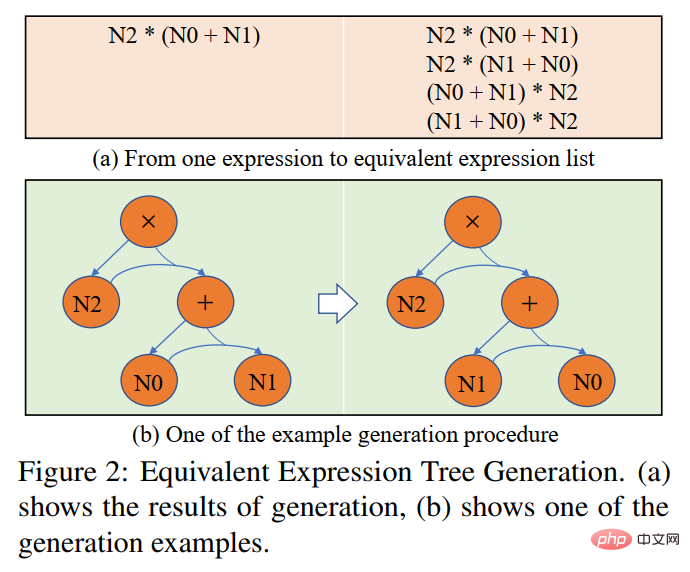
図 5 ニューロジオメトリ プロブレム ソルバー (NGS) の概略図 当社の NGS は主に、テキスト エンコーダー、ジオメトリ エンコーダー、結合推論モジュール、プログラム デコーダーで構成されています。テキスト エンコーダは質問テキストの意味表現を担当し、幾何図形エンコーダは幾何図形の表現を担当します。テキスト表現とグラフィック表現の両方が、マルチモーダル意味論的表現の共同推論モデルに入力され、プログラム デコードのためにプログラム デコーダーに供給され、解釈可能で実行可能な形式的な解決プログラムが出力されます。 さらに、幾何図形エンコーダによる幾何図形の表現能力を強化し、結合推論モジュールを促進して、幾何図形に含まれるマルチモーダル情報を完全に統合して効率的に表現します。モデルの表現能力を向上させ、定理の知識を注入するために、さまざまな補助タスクが実装されています。これらの補助タスクには次のものが含まれます: 1) パズルの位置予測: 幾何学図形を複数のパッチに切り分け、それらをランダムに配置し、次に幾何学エンコーダにそれらを再配置させることによって、幾何学図形のピクセル レベルのグラフィックス理解が達成されます; 2) 幾何学要素の予測: Let幾何学図形エンコーダは、オブジェクトレベルのグラフィックス理解を達成するために、現在の幾何学図形にどの幾何学要素が現れるかを予測することを学習します; 3) 知識点予測: 結合推論モジュールで質問テキスト表現と幾何学図形表現のマルチモーダル融合を実行します。同時に、全体的な問題表現を改善するために、知識ポイント分類タスクが導入されます。 NGS では、パズルの位置予測とジオメトリ要素の予測を使用してジオメトリ エンコーダを事前トレーニングします。ナレッジ ポイント予測タスクは、NGS によるマルチタスク トレーニングのサブタスクとして使用されます。 実験では、記事では GeoQA に基づいて複数のニューラル ネットワーク ベースのベースライン モデルを構築し、NGS をそれらと比較しました。 NGS と GeoQA のベースライン モデルの実験結果を以下の表に示します。 上記の表からわかるように、NGS は GeoQA 上でベースライン モデルよりも優れた問題解決パフォーマンスを達成できます。しかし、幾何学的な問題を解決する上で、さまざまなモデルと人間との間には依然として大きな隔たりがあることもわかります。 さらに、NGS におけるさまざまな設計の有効性を検証するために、さまざまなアブレーション実験を実施しました。研究の詳細については、元の論文を参照してください。 論文 4: 解決バイアスを軽減するための不偏数学文章題ベンチマーク #計算言語学協会の調査結果: NAACL 2022 ##論文アドレス: https://aclanthology.org/2022 。 founding-naacl.104.pdf この研究では、中山大学人間機械知能統合研究室チームが、問題を解決するための現在のベンチマークでの評価を再検討します。数学的応用問題 モデルの解決バイアス。この問題解決バイアスは主にデータ バイアスと学習バイアスによって引き起こされます。データ バイアスとは、トレーニング データ セットが各質問のさまざまな説明方法をすべてカバーできていないという問題を指します。その結果、問題解決モデルは浅い意味論しか学習できず、質問の意味の深い意味論を理解できません。図 6(a) に示すように、問題解決モデルは浅い意味論のみを学習し、それを問題解決に使用するため、問題の問題部分を削除した後でも、問題解決率は 69.4% に達する可能性があります。 学習バイアスとは、MWP は複数の等価式で解くことができるが、現在のデータ セットではラベルとして等価式のうちの 1 つだけが使用されることを意味します。モデルにこのラベルを強制的に学習させる一方、他の同等の方程式を無視すると、学習トレーニングに偏りが生じます。図 6(b) に示すように、トレーニング プロセス中に、モデルは GroundTruth 式と矛盾する式を生成する可能性がありますが、答えは正しいですが、データ セットでは特定の同等の式のみがラベルとして使用されるため、損失関数を計算するとき、式は誤った式であるとみなされ、2 つの正しい式の間の損失が解モデルに逆伝播され、モデルの過剰補正が発生します。 #図 6 データ バイアスと学習バイアスの例 データの偏りを軽減するために、中山大学人間機械知能統合研究室チームは新たな試みを行い、質問事項を可能な限りカバーする方法で新しい MWP のラベルを付け直しました。 .UnbiasedMWP のベンチマーク。基本的な問題として2907問の文章題を集め、各問題に含まれるストーリーを可能な限り多くの問題に注釈を付けました。 手動の注釈プロセスを簡素化するために、まず質問のバックボーンコンテンツに基づいて合理的な表現をいくつか生成し、次に質問を逆に書き直します。合理的な式を生成するために、次の 3 つの式バリアントを設計しました。 1) 変数の組み合わせ (Va) バリアント: 質問のバックボーンから 2 つの数値変数をランダムに選択し、数学演算子 (、-、*、/) を使用してそれらを組み合わせます。たとえば、n0 n1、n0 − n1 などです。 2) 部分式 (Sub) 変換: 元の質問のターゲット式に含まれるすべての部分式が演算子によって変更され、それによって新しい式が得られます。 3) 式全体 (Whole) 変形: 元の質問の対象式に含まれる演算子を変更することで、新しい式を取得します。上記の 3 つのバリエーションから取得された新しい式セットは手動でフィルター処理され、新しい質問で注釈を付けることができない式は除外され、残りの式には手動で質問の注釈が付けられます。 #学習バイアスを軽減するために、動的ターゲット選択戦略を提案します。トレーニング プロセス中に、モデル出力の結果に基づいて、それに近いターゲット式が選択されます。 GroundTruth として。等価な式を取得するには、数学演算の交換法則を使用して式ツリーを変形し、複数の等価な式を取得します。図 7 に示すように。 #図 7 等価式ツリー生成の概略図
動的ターゲット選択戦略が学習バイアスを軽減できるかどうかを検証するために、動的ターゲット選択戦略を複数の問題解決モデルに適用しました。実験結果を以下の表に示します。
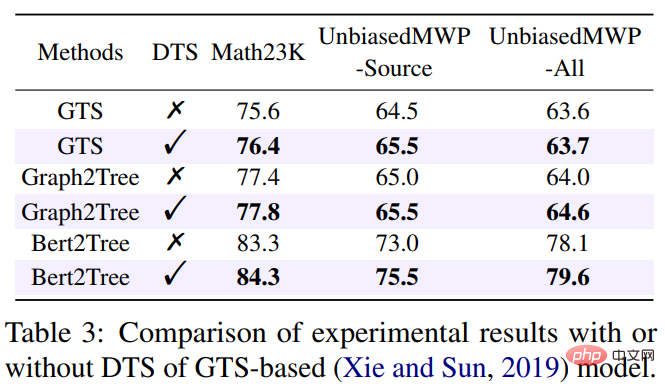
論文 5: LogicSolver: 論理的プロンプト強化学習による解釈可能な数学文章問題の解決に向けて 計算言語学協会の調査結果: EMNLP 2022 #近年、深層学習モデルは、数学的応用問題、特に正確な答えを自動的に解決することに大きな成功を収めています。ただし、これらのモデルは高い解決パフォーマンスを達成するために統計的な手がかり (浅いヒューリスティック) のみを使用しており、問題の背後にある数学的論理を真に理解して推論していないため、これらの方法を説明するのは困難です。 この問題を解決し、解釈可能な数学文章問題解決の分野の発展を促進するために、中山大学人間機械知能統合研究室チームは、最初の高品質の説明数学文章問題データを構築しました。セット、InterMWP。このデータセットには、11,495 個の数学文章問題と、代数知識に基づく 210 個の論理式が含まれており、各文章題の解法表現には論理式が注釈されています。既存の数学応用問題解決データセットとは異なり、当社の InterMWP は、問題ソルバーが解法式を出力するだけでなく、問題ソルバーが解法式に対応する代数知識に基づいた論理式を出力することを要求し、それによってモデルを実現します。出力の。 InterMWP データ セットと他の問題解決データ セットの類似点と相違点を図 8 に示します。具体的なアノテーションのプロセスについては、原文を参照してください。 #図 8 InterMWP データセットの例 数理論理学の知識を活用し、MWP 問題ソルバーに解釈可能性を与えるために、私たちのチームは、図 9 に示すように、新しい数学アプリケーション問題解決フレームワーク LogicSolver をさらに構築しました。このフレームワークは、論理式ライブラリから関連する論理知識を検索を通じてプロンプト情報として抽出し、質問エンコーダによるMWPの意味表現を改善し、MWPの論理説明の生成能力を強化します。 ##図 9 LogicSolver 設計図 実験では、InterMWP データセット上に複数のベースライン モデルを構築し、LogicSolver をこれらのベースライン モデルと比較しました。実験結果を以下の表に示します。
論文 6: UniGeo: 数式の再定式化による幾何学論理的推論の統合 Jiaqi Chen、Tong Li、Jinghui Qin、Pan Lu、Liang Lin、Chongyu Chen、Xiaodan Liang The 2022 Conference on Empirical Methods in Natural Language Processing この目的を達成するために、中山大学人間機械オブジェクト知能統合研究所チームは、数千の幾何学質問を含むベンチマーク データ セット UniGeo を構築しました。 UniGeo には、4,998 の幾何計算問題と 9,543 の幾何証明問題が含まれています。各証明問題に対して複数ステップの証明アノテーションが提供されており、これらのアノテーションは実行可能な記号プログラムに簡単に変換できます。図 10 に示すように、計算問題でも同様の注釈が使用されます。図 10 に示すようにアノテーションを付けた後、UniGeo は幾何学的計算問題と幾何学的証明問題を正式な記号言語で適切に表現できます。 図 10 UniGeo データ サンプル Afterこれら 2 つの質問の統一された表現が幾何計算問題と幾何証明問題に対するモデルの意味理解と記号推論能力を効果的に促進できることを検証するために、形式記号言語を使用して幾何計算問題と幾何証明問題に均一に注釈を付けます。これにより、より多くのことが可能になります。計算問題や証明問題を効率的に解くことができます。中山大学人間機械物体知能統合研究室チームは、図 11 に示すように、幾何学的な問題解決と証明を統合処理して、幾何学的な計算問題と幾何学的な証明問題を同時に処理するための Geoformer を構築しました。 図 11 GeoFormer の図
#図 12 数式事前トレーニングの概念図実験では、UniGeo ベンチマークに基づいて複数のベースライン モデルを構築し、提案した GeoFormer のパフォーマンスを比較しました。実験結果を以下の表に示します。
#実験結果から、私たちが提案した GeoFormer は、計算問題と証明問題の両方でベースライン モデルよりも良い結果が得られることがわかります。 -datasets.全体的なパフォーマンスが良好です。同様に、GeoFormer は、計算問題と証明問題の統合されたソリューションを必要とする完全なデータセットにおける NGS および BERT ベースライン モデルよりも優れています。数式の事前トレーニングと MLM の事前トレーニングの後、GeoFormer の事前トレーニングでは、GeoFormer と比較してパフォーマンスがさらに向上します。これらの実験結果は、GeoFormer の有効性を完全に証明するとともに、幾何計算問題と幾何証明問題の統一モデル推論がそれぞれのタスクにも役立つことを示しています。 この研究は EMNLP2022 のメインカンファレンスに含まれています。研究の詳細については続報をお待ちください。 論文 7: 数学文章題解決のためのテンプレートベースの対比蒸留事前トレーニング Jinghui Qin *、Zhicheng Yang*、Jiaqi Chen、Xiaodan Liang、Liang Lin 深層学習モデルは数学的問題解決の分野で大きな進歩を遂げましたが、これらのモデルは解決策を無視しています。この問題解決ロジックは、多くの場合、解決策テンプレート (ソリューション) に対応します。図 13 に示すように、2 つの異なる文章問題がそれぞれ同じ解決策に対応する可能性があります。
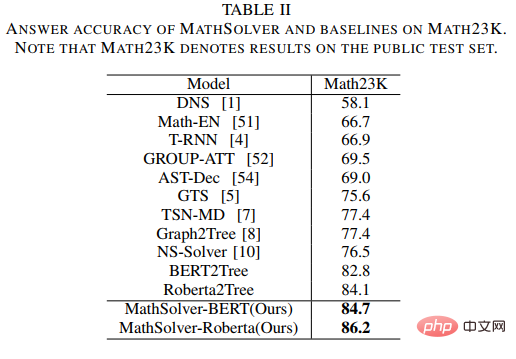
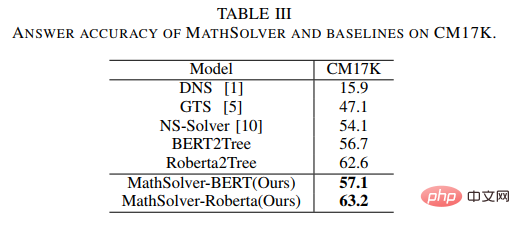
# さらに、事前トレーニングされた言語モデル (PLM) には、MWP の問題の解決に役立つ豊富な知識と高品質の意味表現を持つ機能が含まれています。 事前トレーニングされた言語モデルに含まれる豊富な知識を最大限に活用し、解決ロジックを使用してアプリケーションの問題をより効率的に解決するために、中山大学ヒューマンマシン-オブジェクトインテリジェント統合研究室チームは、事前トレーニングされた言語モデルとの比較に基づいてソリューションテンプレートを提案しました。蒸留事前トレーニングメソッドは、図14に示すように、ソルバーの問題エンコーダーに対してドメイン事前トレーニングを実行します。この方法では、多視点の対比学習を使用して数理論理学の知識を効果的に検討しながら、知識の蒸留を利用して知識と高品質の意味表現能力を事前トレーニングされた言語モデルに効果的に保持します。 具体的には、まず 2 つの質問間の解決テンプレートが一貫しているかどうかを指標として使用し、2 つの質問が表現空間内で互いに近くにあるべきかどうかを判断します。次に、教師エンコーダ、学生エンコーダ、およびそれらに対応する Momentum エンコーダからの比較学習を含む多視点比較学習を提案します。これにより、同じ解決テンプレートを持つ 2 つの質問表現が教師表現空間と学生表現空間で相互作用できます。ソリューション ロジックの注入を実現するには、スペースに近づきます。さらに、事前トレーニングされた言語モデルで初期化されたスチューデント エンコーダに含まれる知識と高品質な表現機能を可能な限り保持するために、知識の蒸留を使用して、特徴表現を使用してスチューデント エンコーダの表現を制限します。教師エンコーダの監視としての訓練された教師エンコーダと同じ表現能力を持ち、それによって意味の保存が達成されます。 図 14 ソリューション テンプレートと事前トレーニング済み言語モデルに基づく蒸留事前トレーニング方法の比較 #実験では、初期化としてさまざまな事前トレーニング済み言語モデルを使用し、メソッドの効果を検証します。問題エンコーダ MathEncoder をそれぞれ BERT ベースと Roberta ベースの重みで初期化し、GTS のデコーダを式デコーダとして使用します。 MathEncoder に基づくソルバーを総称して MathSolver と呼びます。 MathSolver と Math23K および CM17K の複数のメソッドを比較しました。実験結果を以下の表に示します。
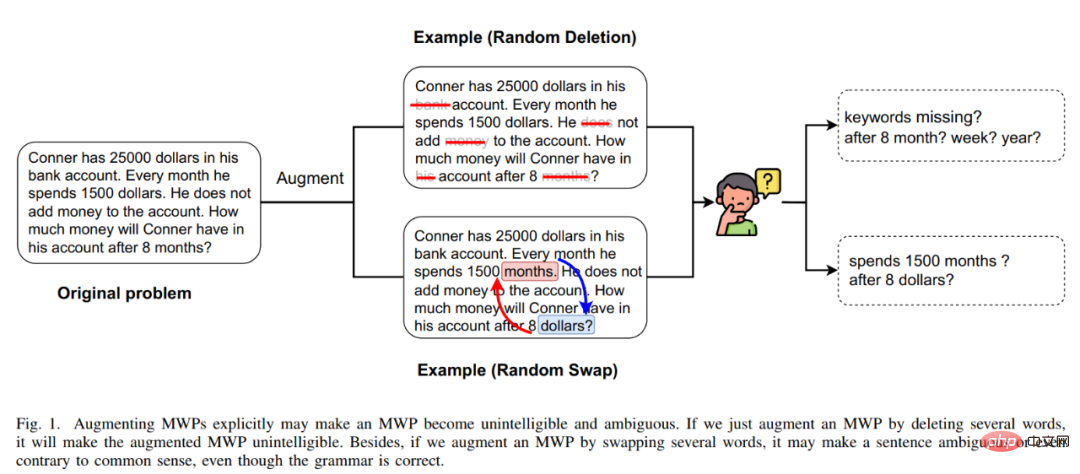
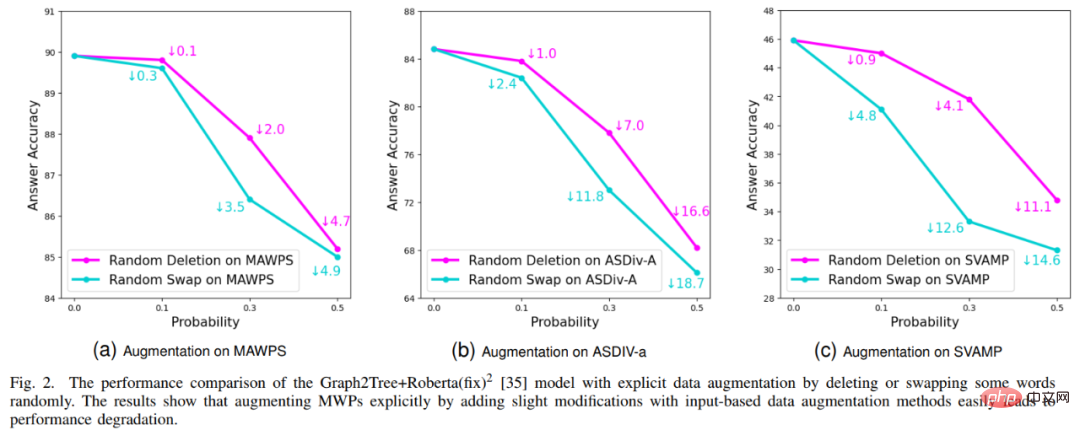
論文 8: 数学の文章問題解決者をトレーニングするための内省的データ拡張手法 #Jinghui Qin、Zhongzhan Huang、Ying Zeng、Liang Lin MWP のデータ ボトルネックの問題により、費用対効果の高いデータ拡張手法を使用してデータ利用効率を向上させ、ソルバーのパフォーマンスを向上させる方法を考えることが促されます。最も直接的なデータ拡張方法は、一般的に使用される文字置換、文字削除などの入力に基づくデータ拡張方法です。しかし、MWP には簡潔性と簡潔性という特性があるため、このタイプの方法は MWP には適していません。入力した文章が乱れたり、質問の意味が不明瞭になる可能性があります。また、質問の意味に含まれる数学的関係は変更できませんが、この種の方法では、図 15 に示すように、質問の意味に含まれる数学的関係が変更される可能性があります。 #図 15 MWP タスクに適用できない入力ベースのデータ拡張方法の例 # さらに、中山大学人間・機械・物体知能統合研究室チームも入力ベースのデータ強化手法について一定の検証を行い、その実験結果を図 16 に示します。実験結果は、入力ベースの明示的なデータ拡張方法は MWP タスクには適用できず、MWP タスクが遭遇するデータ ボトルネックの問題を効果的に軽減できないことを示しています。 #図 16 入力ベースのデータ拡張方法では MWP の問題解決効果を向上させることはできません
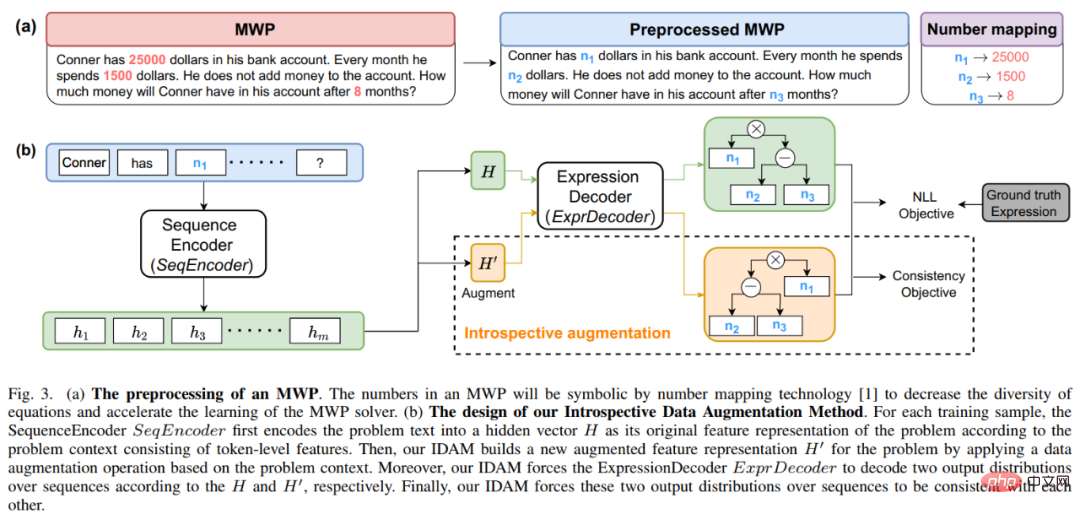
図 17 内省的データ拡張手法 (IDAM) の概略図 #実験では、IDAM を複数の SOTA メソッドに埋め込み、それらを複数のデータセットで比較し、IDAM メソッドの有効性と汎用性を検証しました。実験結果を以下の表に示します。実験結果から、同じ実験構成の下で、IDAM が異なる MWP データ セット上の異なるソルバー ベースライン モデルのパフォーマンスを向上できることがわかります。これは、MWP 問題に対する IDAM アプローチの有効性を完全に示しています。 この結果は、音声、音声、言語処理に関する IEEE/ACM トランザクションに送信されました。詳細については、しばらくお待ちください。 研究室紹介 孫文大学ヒューマン・コンピュータ・サイバー・インテリジェント融合研究室 (HCP Lab) は 2010 年に設立されました。林梁教授による最先端の人工知能技術のレイアウトに関する研究テーマは、中国画像グラフィック協会の科学技術賞一等賞、呉文軍自然科学賞、省自然科学一等賞を受賞しました。その他の栄誉もあり、梁暁丹や王克澤など国家レベルの若手人材を育成してきました。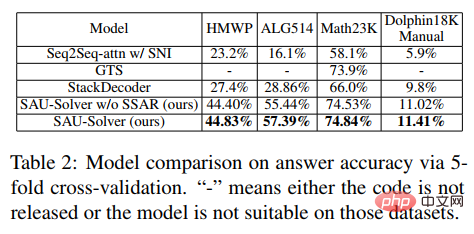 
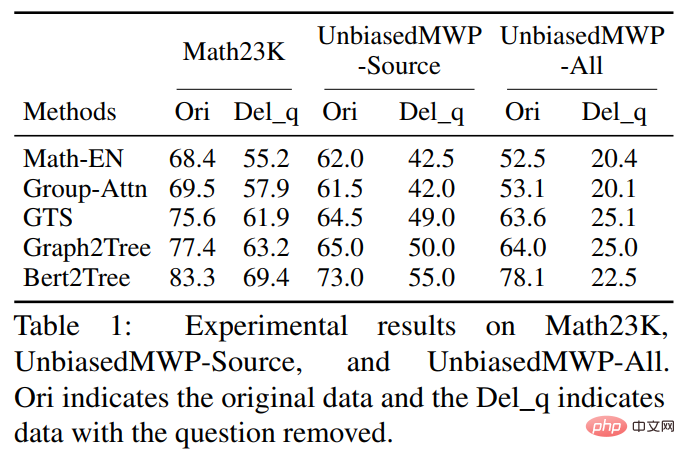
#実験結果から、動的ターゲット選択戦略が学習バイアスを効果的に軽減し、モデルの解法効果を向上させることができることがわかります。研究の詳細については、元の論文を参照してください。 
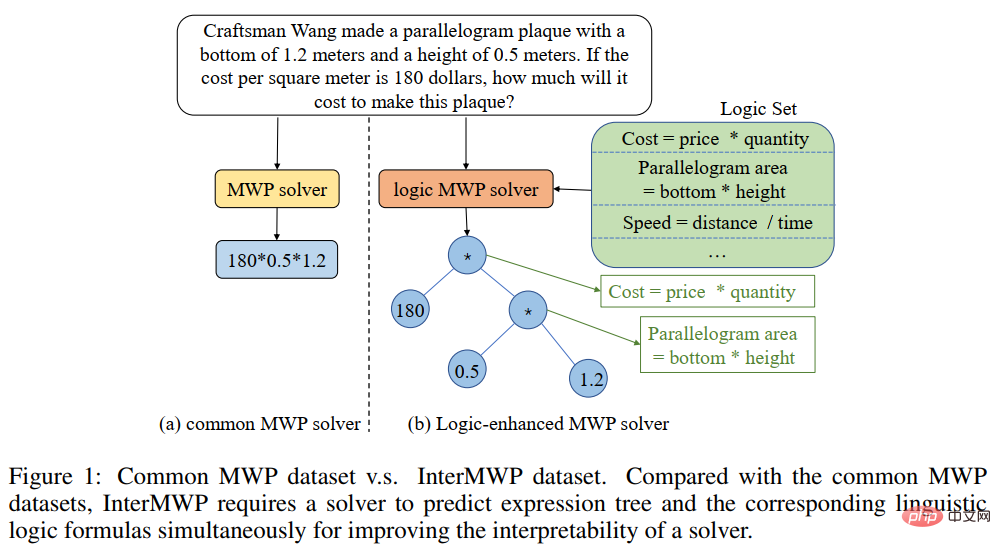
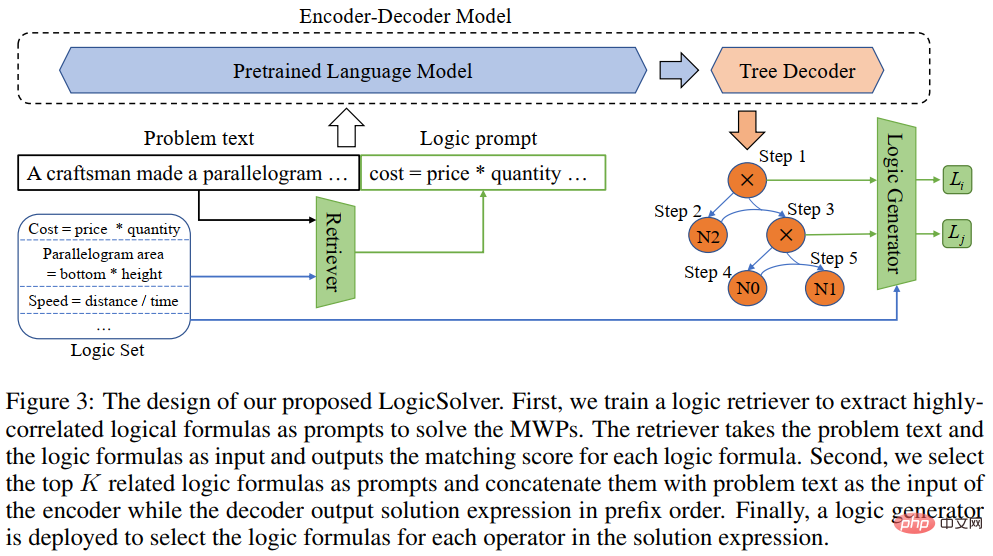
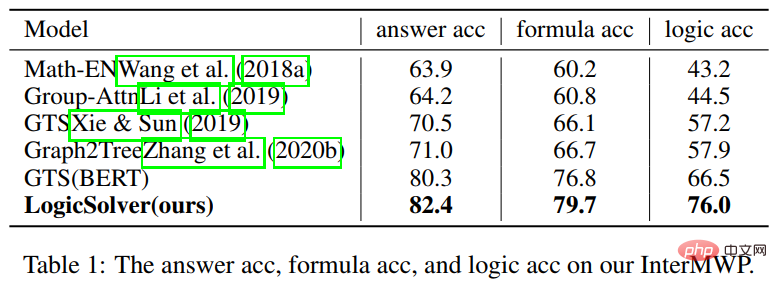
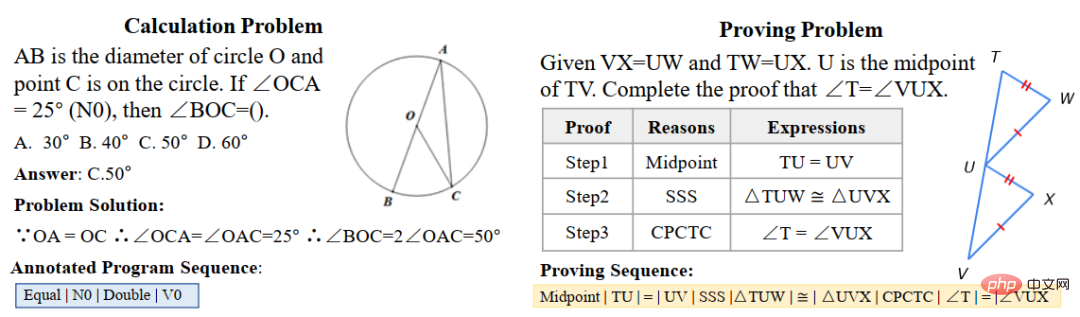
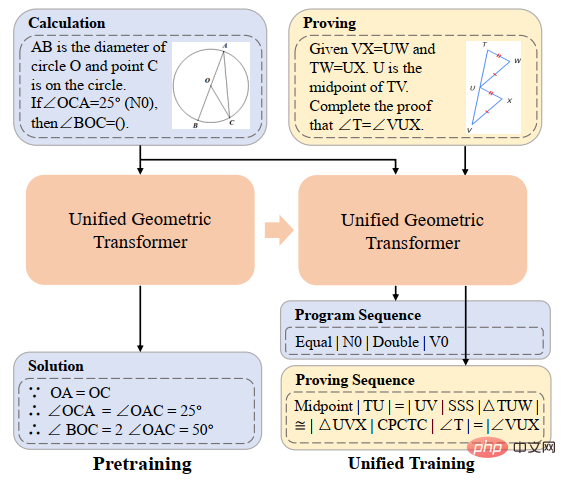
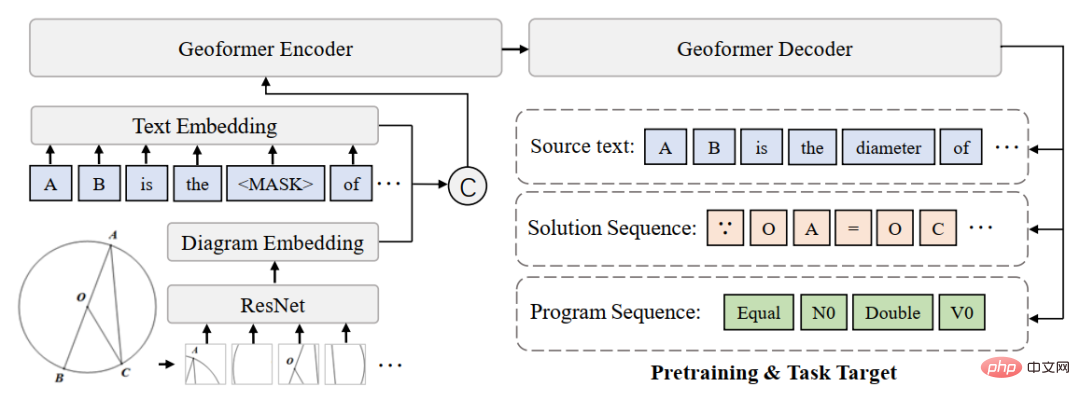
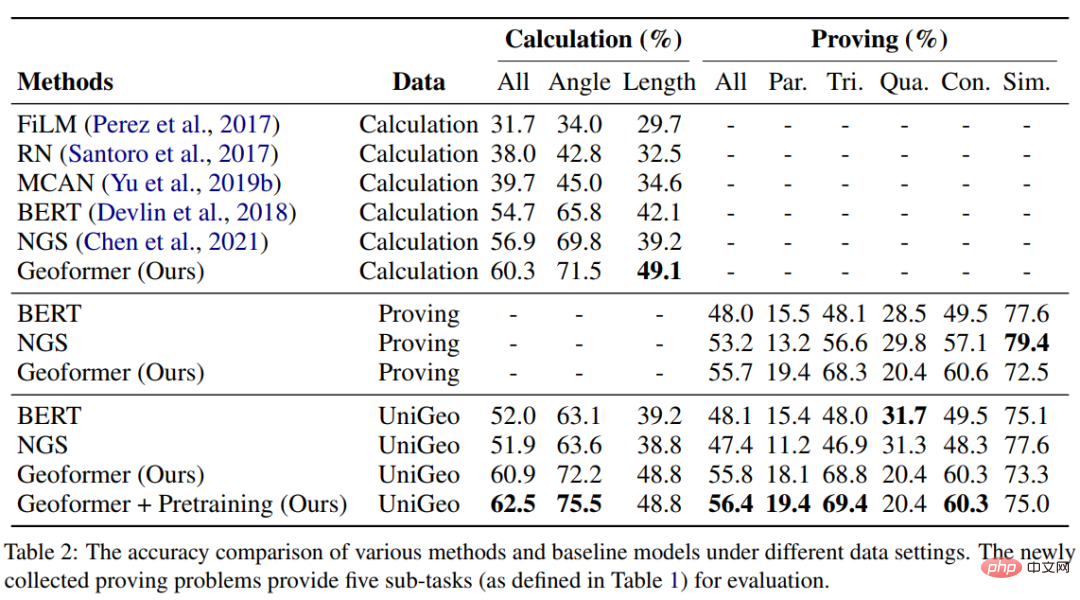
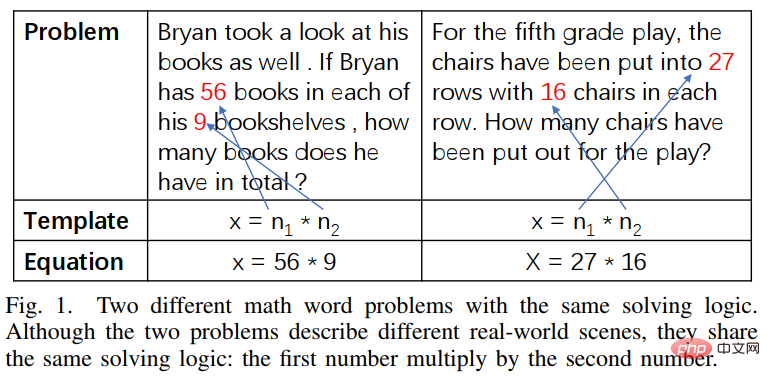図 13 言語の説明は異なるが、解決策は同じ文章題の例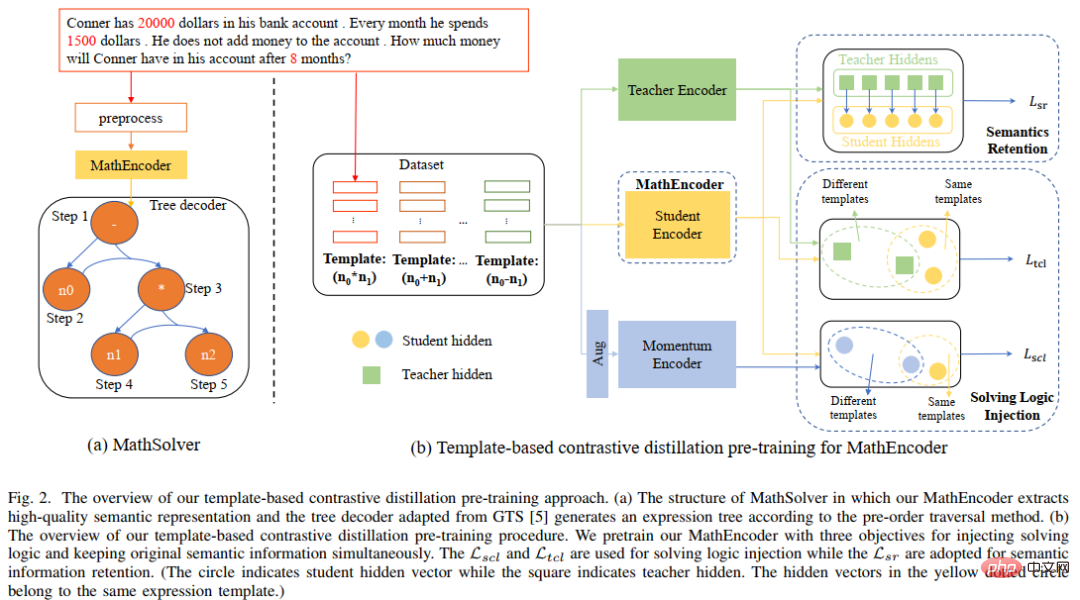
以上が中山大学の HCP Lab チーム: AI の問題解決における新たなブレークスルー、ニューラル ネットワークが数学的推論への扉を開くの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
