Michael Bronstein は、代数トポロジーを基にして、新しいグラフ ニューラル ネットワーク コンピューティング構造を提案します。
この記事は、Cristian Bodnar と Fabrizio Frasca の共著で、C. Bodnar、F. Frasca らによって 2021 ICML「Weisfeiler and Lehman Go Topological: Information Transfer Simple Network」および 2021 NeurIPS に掲載されました。 Weisfeiler and Lehman Go Cellular: CW Network」の論文を参考資料として使用します。
この記事は、微分幾何学と代数トポロジーの観点から見たグラフ ニューラル ネットワーク シリーズの議論の一部にすぎません。
グラフを使用すると、コンピューター ネットワークから大型ハドロン衝突型加速器での粒子相互作用に至るまで、あらゆるものをモデル化できます。グラフは、その離散的かつ組み合わせ的な性質により、計算が容易でありながら抽象的な関係を表現できるため、いたるところに普及しています。人気の理由の 1 つは、グラフがジオメトリ (空間内のノードの位置やエッジの曲がり方など) を抽象化し、ノードがどのように接続されているかの表現のみを残すことです。
グラフ理論は、レオンハルト オイラーの 1741 年の著書『Geometria situs』での観察に由来し、そこで彼は有名なケーニヒスベルクの 7 つの橋問題を指摘しました。この問題には解決策がありません。
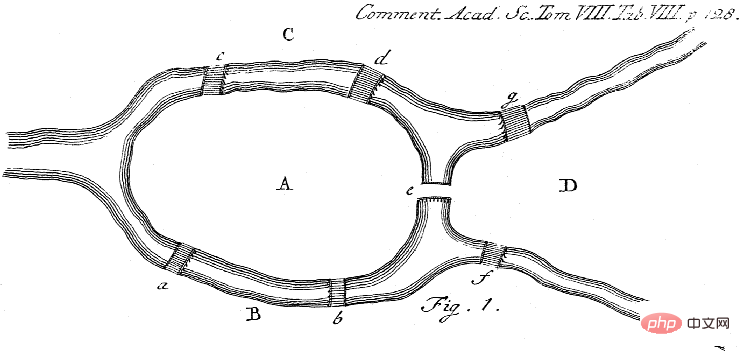
注: 7 つの橋の問題では、橋を何度も渡らずにケーニヒスベルクの円形の歩行ルートを見つける必要があります。オイラーが言ったように、ケーニヒスベルク市の正確な形状は重要ではなく、重要なのは異なる土地 (グラフのノード) がどのように互いに (エッジ) 接続されているかです。オイラーは、すべてのノードが偶数次数を持つ場合にのみ、そのようなサイクルが存在することを示しました。さらに、元の橋のうち現代まで残っているのは 5 つだけです。出典: Wikipedia
興味深いことに、オイラーの発見はグラフ理論の始まりとなっただけでなく、トポロジーの誕生ともみなされることがよくあります。グラフと同様に、トポロジストは、特定の形状や幾何学構造から独立した空間の特性に興味を持っています。
これらのアイデアの現代的な表現は、アンリ ポアンカレによる独創的な論文である 1895 年の「分析状況」に現れており、その研究は対流を引き起こしました。 形状の組み合わせ記述は興味深いものであり、トポロジー的不変量は以下のとおりです。これらの多様体からより簡単に見つけて計算できます。
キャプション: レオンハルト・オイラー (1707-1783) とアンリ・ポアンカレ (1854-1912)
これらの組み合わせ記述は今日セル複合体として知られており、グラフの高次元一般化と考えることができます。
ノードとエッジによって形成されるグラフとは異なり、セル複合体には高次元の構造または「セル」を含めることもできます。頂点は 0 セル、エッジは 1 セル、2D 表面は 2 です。 -細胞など細胞複合体を構築するには、1 つの細胞の境界を他の低次元の細胞に接着することで層状にします。
特殊なケースでは、セルが単体 (エッジ、三角形、四面体など) で構成されている場合、これらの空間は単体複合体とも呼ばれます。

注: グラフは、エッジ (1 セル) を接続する頂点のセットとして見ることができます。同様に、単一細胞複合体と細胞複合体は、2 つのセル (青で表示)、3 つのセル (緑で表示) などを接続したグラフとして見ることができます。
1 機械学習とデータ サイエンスにおけるトポロジー私たちは、トポロジーが実用的なツールになるまで 400 年も待つ必要はないと信じています。
トポロジカル データ分析 (TDA) の傘下では、浅い複合材料などのトポロジカル構造が機械学習やデータ サイエンスで使用されてきました。このタイプの手法は 1990 年代に登場しました。メトリックに依存せず、ノイズに強い方法で「データの形状」を分析しようとします。
TDA のルーツは、1920 年代後半の最も多作な地質学者の 1 人、レオポルド ベトナム オリスの研究に遡ります。ただし、これらのテクノロジーを大規模に適用するには、現代のコンピューティングの出現まで待たなければなりませんでした。

# 凡例: 点群が与えられた場合、各点の周りの固定半径の閉じた球間の交差により、単純な複合体が生成されます。球の半径を徐々に大きくすることで、単純な複合体のネストされたシーケンスを取得できます。画像出典: バスティアン・リーク。
#TDA の主力は、点群から位相特徴を抽出する方法である Persistent Homology (PH) です。点のデータセットが与えられると、PH は単純な複素数のネストされたシーケンスを作成します。各複素数は、分析される基礎となる点群の特定のスケールに対応します。次に、スケールが徐々に大きくなり、シーケンス内の 1 つの複合体から次の複合体に移行するにつれて現れたり消えたりするさまざまなトポロジ上の特徴 (接続されたコンポーネント、ループ、穴など) を追跡します。
深層学習の時代では、永続的相同性は「第二の人生」を持っています。これは、永続的相同性を介して逆伝播を実行できることを示しており、既に変換できることを示しているためです。確立された TDA デバイスは次のとおりです。深層学習フレームワークに統合されています。
最近の一連の研究では、実行されるデータと計算をサポートするためのより豊かな基盤となる位相空間として、幾何学的な深層学習における単純化と細胞複合体のさまざまな使用法を提案しています。
このアイデアを活用する最初のいくつかの研究では、単純化された複素数で動作する畳み込みモデルとランダム ウォーク法が提案されました。この記事のように、畳み込みモデルは、細胞の複合体における情報伝達の単純かつ具体的な例として理解できます。
計算はこれらの空間の位相構造 (つまり近傍構造) によって行われるため、この方法を位相情報の受け渡しと呼びます。このフレームワークでは、次の図に示すように、おそらく異なる次元の隣接するユニットが情報を交換します。
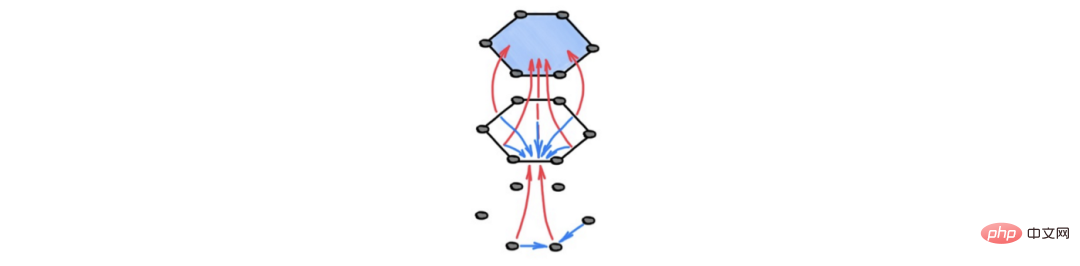
# 注: トポロジ情報伝送の概略図。青い矢印は、上層の隣接するセル、つまり同じ高次元セルの境界上のセル間の「水平」情報伝播を表します。赤い矢印は「垂直」情報伝播を示しており、セルはその境界で低次元のセルから情報を受け取ります。この計算は、境界セルからの情報をより粗い表現に要約することによって、(微分可能な) アンサンブル形式として解釈できます。 GNN のグラフを超えて
細胞複合体によって提供される豊富な構造にもかかわらず、機械学習のトポロジー オブジェクトではグラフが断然最も一般的であることを無視することはできません。であり、それらを超えるデータセットはほとんどありません。それにもかかわらず、入力グラフを変換することによって、これらの興味深い位相空間を活用することができます。グラフを高次元の位相空間に変換することを、圏論における同じ名前の概念に似せて「リフティング」と呼びます。一定のルールに従って入力グラフに高次元のセルを追加する変換です。たとえば、グラフの各クリフまたはサイクルに高次元のセルを接続することにより、グラフをセル複合体に昇格させることができます。これを行うことにより、グラフはより多くの構造を持つ別の空間に置き換えられ、元のグラフよりも優れた計算構造を GNN に提供できます。以下では、このアプローチの具体的な利点について説明します。
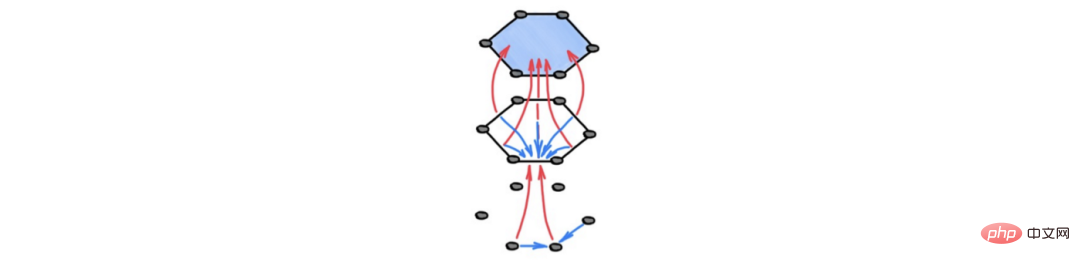
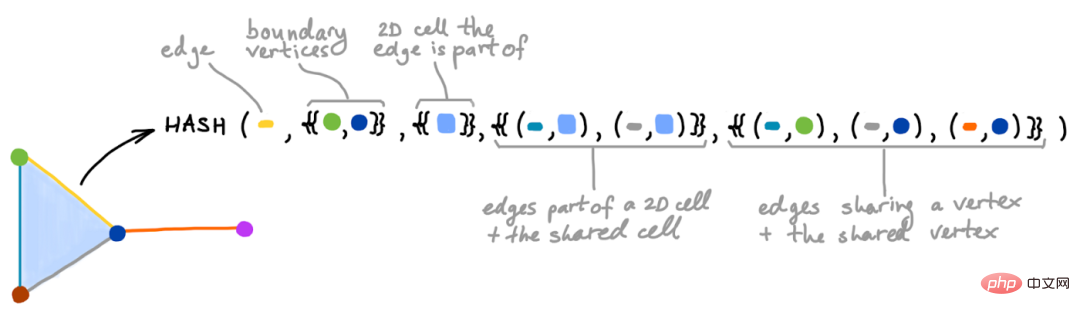
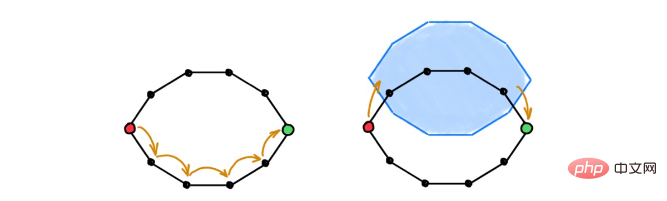
凡例: 2 次元の閉じた円板の境界を図の誘導ループに接着すると、次のように取得できます。図 高次元の細胞複合体を構築する。 GNN は通常、ノード中心のビューを採用しており、エッジに存在するデータは頂点間の通信を増やすための補助情報としてのみ見なされます。トポロジカル情報転送では、すべてのユニットが第一級市民です。それらの寸法に関係なく、それらには特定の表現が割り当てられ、それは隣接するユニットと情報を交換することによって開発されます。これは、特定の高次構造とそれらの間の相互作用を明示的にモデル化するためのレシピを提供します。特に、 これは、入力グラフのエッジ (つまり 1 ユニット) 特徴を進化させるための原則に基づいたアプローチを提供します。これは、大規模なクラスの GNN モデルでは考慮されない問題です。 図は定義上、バイナリ (「ペアごと」) であり、3 つ以上のオブジェクトが関与する関係や相互作用を表すことはできません。これは、高次の相互作用を特徴とする複雑なシステムをモデル化する場合に問題になる可能性があります。たとえば、化学反応における 3 つの反応物質が同時に相互作用する可能性があります。細胞複合体では、この状況は 2 つの細胞間の反応物を接続することによってコード化できます (つまり、「塗りつぶされた」三角形)。したがって、モデルの計算フローは高次相互作用の存在に適応されます。 凡例: 細胞ワイスフェイラー・リーマン (CWL) 検定。古典的な WL 検定を細胞集団に拡張した、アルゴリズムの各ステップどちらも、隣接するセルの色を完全にハッシュします (次元が異なる場合があります)。 情報伝達 GNN の表現能力は、Weisfeiler-Leman (WL) グラフ同型性テストによって制限されます。三角形やサイクルなどの部分構造は、非常に単純な非同形グラフとさえ区別できません。 以前の論文によると (論文アドレス: https://arxiv.org/abs/2103.03212; https://arxiv.org/ abs /2106.12575)、WL テスト (CWL) の細胞バージョンを使用して、細胞複合体の同型性をテストできます。この新しいテストを上記のグラフ リフティング手順と照合すると、WL テストよりも大きなグラフ クラスを区別できることがわかります。したがって、特定の条件下では、トポロジカル情報伝達プロセスは、このテストの利点を継承し、標準の GNN と比較して表現能力が向上します。 不十分、過剰な平滑化、およびボトルネック 情報 を交換できない場合、この現象はアンダーリーチと呼ばれます。 高次元セルによって誘発されるより豊かな近傍構造により、遠く離れたノード間にショートカットが作成されるため、セル複合体はこれらの問題を軽減できます。したがって、情報が有効であるためには、情報に広めるためのいくつかの計算ステップが含まれているだけで十分です。
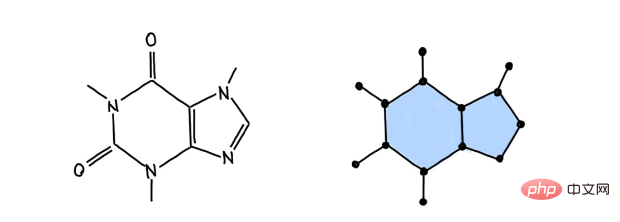
階層モデリング 情報の受け渡しによる計算は階層的であり、情報は低次元の単位から高次元の単位へと流れます。 -次元単位: 次元単位とその逆は、標準的なグラフ ニューラル ネットワークの「水平」プーリングではなく、「垂直」(微分可能な) プーリングの形式と考えることができます。これにより、GNN プーリングベースのパフォーマンスに悪影響を与える入力グラフの詳細な情報を無視することなく、「圧縮された」グラフ領域の誘導バイアスが保存されます。 注: トポロジ情報転送により、異なる次元のユニット間で情報が階層的に存在できるようになります。 特定のアプリケーションは、細胞複合体の構造と自然に一致します。たとえば、分子の原子、結合、化学環は、0 セル、1 セル、および 2 セルとして表すことができ、分子の物理構造間の直接的なつながりになります。対応により、トポロジカル情報伝達で上記の特性を利用できるようになり、これらの表現は、分子特性予測タスクにおけるトポロジカル情報伝達によって達成される最先端の結果も実証します。
穴代数と方向等価性
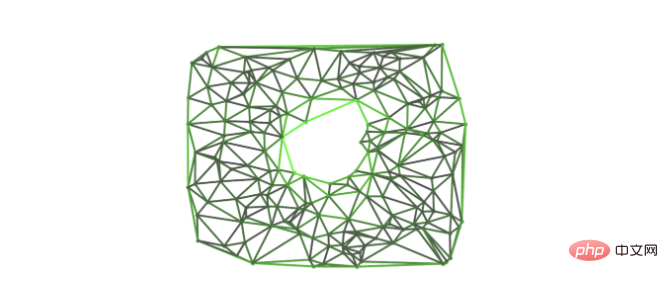
#トポロジカル情報伝達は、代数演算子 (境界演算子など) の (非線形) 一般化として見ることができます。したがって、位相情報の受け渡しも同様に動作する必要があります。つまり、各層の出力が入力複合体の方向の変化に「均一に」応答する必要があります。言い換えれば、レイヤーの方向が同等であることが必要です。私たちの研究では、やはり純粋な畳み込み設定において、適切な非線形性と情報伝達関数を選択することによって、トポロジカルな情報伝達がこの特性をどのように満たすかを研究しています。 位相空間を区別する既知の最も初期の位相不変量の 1 つであるオイラー特性は、もともとプラトン立体の分類に使用されていました。次元内のセル数の合計。驚くべきことに、2 つの細胞複合体が同型である場合、たとえ同じ空間の異なる離散化であっても、これらの合計は一貫しています。 興味深いことに、トポロジ情報伝達モデルの読み出し操作では、各次元単位に包含を適用するため、トポロジの不変性の計算が容易になります。 離散ホッジ理論は、細胞複合体のトポロジカルな特性をより幾何学的に説明します。 k セルに関連付けられたフィーチャの符号が k セルの方向に依存する場合、これらのフィーチャは数学的に、微分幾何学における微分 k 形状の離散バージョン (つまり、k 次元のボリューム要素) として見ることができます。一体型)。 Hoch Laplacian と呼ばれる演算子は、グラフィック ラプラシアンを一般化し、これらの微分形式を操作します。 このラプラシアン演算子に基づく拡散偏微分方程式は、限界内の複合材料の穴に関連する信号に収束することが証明できます。 注: Hoch Laplace 演算子に基づく拡散偏微分方程式は、初期微分形式に収束します。 射影の極限ラプラシアンカーネル上で。この画像は、ホッホ ラプラシアンのゼロ固有ベクトルが複合体の穴の周囲でどのように高い値をとるかを示しています。 最初の単純なニューラル ネットワーク モデルは、実際には Hoch Laplace の畳み込みモデルに基づいており、トポロジカル信号処理からインスピレーションを受けています。つい最近、この演算子に基づく畳み込みモデルのバージョンが、計算代数トポロジにおける NP 困難問題を解くために使用されました。 最近の論文では、とりわけ、トポロジカル情報伝達手法は、細胞複合体の構造をエンコードした変更されたグラフ上で情報伝達を操作する GNN にすぎないと主張しています。これは、情報伝達の計算にセルのペアが関与する畳み込みモデルにも当てはまります。 ただし、最も一般的な形式では、情報関数により、高次元セルが境界上の低次元セル間で受け渡されるエネルギーを調整できます。一般に、エッジは 2 つのノードを正確に接続し、2 セルは必要な数のエッジを接続できるため、情報はグラフ上の通常の 情報を介して渡すことができます。 どちらの場合も、計算は、データがアタッチされている基礎となる空間のトポロジによって駆動されます。私たちは、情報転送にこのトポロジカルな観点を採用することの利点は、純粋に計算上の考慮事項を超えて広がると信じています。貴重な数学的つながりに加えて、研究の議論を他の数学および計算分野に広げ、単調になりがちなコミュニティ間での積極的な相互受精を促進します。 私たちは、トポロジカル情報転送方法について 2 つの主な将来の方向性を予測しています: 第一に、長年にわたって GNN で開発された多くのアーキテクチャ (メカニズム)は、その特有の特性を活用しながら、これらの新しい位相空間に採用される可能性があります。 #第 2 に、代数トポロジーの分野からのより多くの数学オブジェクトやツール (ハニカム プーリーなどの構造を含む) は、最も数学に精通した ML 研究者にとっても魅力的です。 、これも彼らにとっては異質に聞こえるかもしれません) は、グラフおよび幾何学的な深層学習コミュニティによって採用されるでしょう。 これらのメソッドは、古い問題に対する答えを提供し、新しい問題の解決に役立ちます。ロバート グリストが言ったように、「新しい課題には新しい数学が必要です」(新しい課題には新しい数学が必要です) 新しい数学)。 高次の特徴と構造
高次の相互作用
表現力
トポロジー
情報ドメイン アライメント
2 トポロジーと微分幾何の組み合わせ
代数トポロジーでは、各単体に任意の「方向」がある有向単純複素数を使用するのが一般的です。各エッジでソース ノードとターゲット ノードを選択し、三角形ごとにそのノードをトラバースする順序を選択します。方向を選択すると、「境界演算子」を介して特定の単体の境界を計算するなど、複雑な形状に対して興味深い代数演算子を実行できます。これらの代数演算は、単純複合体の「穴」、つまり境界を持たないが他のものの境界上にない領域を見つけるために使用することもできます。舞台裏では、永続的な相同性はこれらの計算に依存してトポロジカルな特徴を検出します。
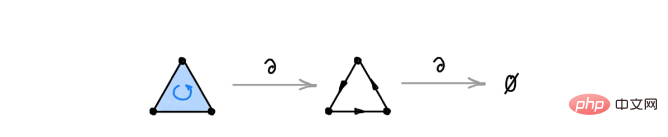 # 凡例: 2 シンプレックスに適用される境界演算子は三角形を生成します。三角形に演算子を再度適用すると、三角形は境界のないサイクルであるため、結果はゼロになります。
# 凡例: 2 シンプレックスに適用される境界演算子は三角形を生成します。三角形に演算子を再度適用すると、三角形は境界のないサイクルであるため、結果はゼロになります。 離散ホッジ理論
3 最終的な考察
これらは単なる偽装グラフなのでしょうか?
以上がMichael Bronstein は、代数トポロジーを基にして、新しいグラフ ニューラル ネットワーク コンピューティング構造を提案します。の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7748
7748
 15
15
 1643
1643
 14
14
 1397
1397
 52
52
 1291
1291
 25
25
 1234
1234
 29
29
 CUDA の汎用行列乗算: 入門から習熟まで!
Mar 25, 2024 pm 12:30 PM
CUDA の汎用行列乗算: 入門から習熟まで!
Mar 25, 2024 pm 12:30 PM
General Matrix Multiplication (GEMM) は、多くのアプリケーションやアルゴリズムの重要な部分であり、コンピューター ハードウェアのパフォーマンスを評価するための重要な指標の 1 つでもあります。 GEMM の実装に関する徹底的な調査と最適化は、ハイ パフォーマンス コンピューティングとソフトウェア システムとハードウェア システムの関係をより深く理解するのに役立ちます。コンピューター サイエンスでは、GEMM を効果的に最適化すると、計算速度が向上し、リソースが節約されます。これは、コンピューター システムの全体的なパフォーマンスを向上させるために非常に重要です。 GEMM の動作原理と最適化方法を深く理解することは、最新のコンピューティング ハードウェアの可能性をより有効に活用し、さまざまな複雑なコンピューティング タスクに対してより効率的なソリューションを提供するのに役立ちます。 GEMMのパフォーマンスを最適化することで
 Word文書で足し算、引き算、掛け算、割り算を計算する方法
Mar 19, 2024 pm 08:13 PM
Word文書で足し算、引き算、掛け算、割り算を計算する方法
Mar 19, 2024 pm 08:13 PM
WORD は強力なワード プロセッサです。Word を使用してさまざまなテキストを編集できます。Excel の表では、足し算、引き算、乗算の計算方法をマスターしました。そのため、Word の表で数値の足し算を計算する必要がある場合は、乗数を引くにはどうすればよいですか? 計算には電卓しか使用できませんか?答えはもちろん「いいえ」です。WORD でも実行できます。今日は、Word文書の表で加算、減算、乗算、除算などの基本的な演算を数式を使って計算する方法を説明しますので、一緒に学びましょう。そこで、今日は、WORD 文書で加算、減算、乗算、除算を計算する方法を詳しく説明します。ステップ 1: WORD を開き、ツールバーの [挿入] の下にある [表] をクリックし、ドロップダウン メニューに表を挿入します。
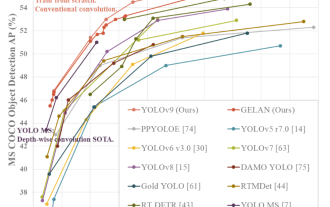 YOLOは不滅です! YOLOv9 がリリースされました: パフォーマンスとスピード SOTA~
Feb 26, 2024 am 11:31 AM
YOLOは不滅です! YOLOv9 がリリースされました: パフォーマンスとスピード SOTA~
Feb 26, 2024 am 11:31 AM
現在の深層学習手法は、モデルの予測結果が実際の状況に最も近くなるように、最適な目的関数を設計することに重点を置いています。同時に、予測に十分な情報を取得するには、適切なアーキテクチャを設計する必要があります。既存の方法は、入力データがレイヤーごとの特徴抽出と空間変換を受けると、大量の情報が失われるという事実を無視しています。この記事では、ディープネットワークを介してデータを送信する際の重要な問題、つまり情報のボトルネックと可逆機能について詳しく説明します。これに基づいて、深層ネットワークが複数の目的を達成するために必要なさまざまな変化に対処するために、プログラマブル勾配情報 (PGI) の概念が提案されています。 PGI は、目的関数を計算するためのターゲット タスクに完全な入力情報を提供することで、ネットワークの重みを更新するための信頼できる勾配情報を取得できます。さらに、新しい軽量ネットワーク フレームワークが設計されています。
 Python の count() 関数を使用してリスト内の要素の数を数える方法
Nov 18, 2023 pm 02:53 PM
Python の count() 関数を使用してリスト内の要素の数を数える方法
Nov 18, 2023 pm 02:53 PM
Python の count() 関数を使用してリスト内の要素の数を計算する方法には、特定のコード サンプルが必要です。Python は強力で習得しやすいプログラミング言語として、さまざまなデータ構造を処理するための組み込み関数を多数提供しています。その 1 つは count() 関数で、リスト内の要素の数をカウントするために使用できます。この記事では、count()関数の使い方と具体的なコード例を詳しく説明します。 count() 関数は Python の組み込み関数であり、特定の値を計算するために使用されます。
 行列式を使用して三角形の面積を計算するJavaプログラム
Aug 31, 2023 am 10:17 AM
行列式を使用して三角形の面積を計算するJavaプログラム
Aug 31, 2023 am 10:17 AM
はじめに 行列式を使用して三角形の面積を計算する Java プログラムは、3 つの頂点の座標を指定して三角形の面積を計算できる簡潔で効率的なプログラムです。このプログラムは、Java で基本的な算術および代数計算を使用する方法と、Scanner クラスを使用してユーザー入力を読み取る方法を示しているため、ジオメトリを学習または操作する人にとって役立ちます。プログラムはユーザーに三角形の 3 点の座標を入力するように要求し、その座標が読み取られて、座標行列の行列式を計算するために使用されます。行列式の絶対値を使用して面積が常に正であることを確認し、式を使用して三角形の面積を計算し、ユーザーに表示します。このプログラムは簡単に変更して、さまざまな形式での入力を受け入れたり、追加の計算を実行したりできるため、幾何学的計算のための多用途ツールになります。決定要因のランク
 Java で部分文字列の出現数を再帰的にカウントする
Sep 17, 2023 pm 07:49 PM
Java で部分文字列の出現数を再帰的にカウントする
Sep 17, 2023 pm 07:49 PM
2 つの文字列 str_1 と str_2 を指定します。目的は、再帰的プロシージャを使用して、文字列 str1 内の部分文字列 str2 の出現数をカウントすることです。再帰関数は、その定義内で自分自身を呼び出す関数です。 str1 が「Iknowthatyouknowthatiknow」、str2 が「know」の場合、出現回数は -3 になります。例を通して理解しましょう。たとえば、入力 str1="TPisTPareTPamTP"、str2="TP"; 出力 Countofoccurrencesofasubstringrecursi
 1.3ミリ秒には1.3ミリ秒かかります。清華社の最新オープンソース モバイル ニューラル ネットワーク アーキテクチャ RepViT
Mar 11, 2024 pm 12:07 PM
1.3ミリ秒には1.3ミリ秒かかります。清華社の最新オープンソース モバイル ニューラル ネットワーク アーキテクチャ RepViT
Mar 11, 2024 pm 12:07 PM
論文のアドレス: https://arxiv.org/abs/2307.09283 コードのアドレス: https://github.com/THU-MIG/RepViTRepViT は、モバイル ViT アーキテクチャで優れたパフォーマンスを発揮し、大きな利点を示します。次に、この研究の貢献を検討します。記事では、主にモデルがグローバル表現を学習できるようにするマルチヘッド セルフ アテンション モジュール (MSHA) のおかげで、軽量 ViT は一般的に視覚タスクにおいて軽量 CNN よりも優れたパフォーマンスを発揮すると述べられています。ただし、軽量 ViT と軽量 CNN のアーキテクチャの違いは十分に研究されていません。この研究では、著者らは軽量の ViT を効果的なシステムに統合しました。
 C# で Math.Pow 関数を使用して指定した数値のべき乗を計算する方法
Nov 18, 2023 am 11:32 AM
C# で Math.Pow 関数を使用して指定した数値のべき乗を計算する方法
Nov 18, 2023 am 11:32 AM
C# には、多くの数学関数が含まれる Math クラス ライブラリがあります。これらには、累乗を計算する関数 Math.Pow が含まれており、指定された数値の累乗を計算するのに役立ちます。 Math.Pow 関数の使用法は非常に簡単で、基数と指数を指定するだけです。構文は次のとおりです: Math.Pow(base,exponent); ここで、base は基数を表し、exponent は指数を表します。この関数は double 型の結果、つまりべき乗の計算結果を返します。しましょう




