Pythonデータ分析モジュールNumpyのスライス、インデックス作成、ブロードキャストについて詳しく解説

Numpy のスライスとインデックス付け

ndarray オブジェクトの内容は、Python のリストのスライス操作と同様に、インデックス付けまたはスライスを通じてアクセスおよび変更できます。

ndarray 配列は、0 ～ n-1 の添字に基づいてインデックスを付けることができます。スライス オブジェクトは、組み込みのスライス関数と開始の設定を通じて元の配列から取得できます。 stop パラメータと step パラメータ 新しい配列を切り出します。

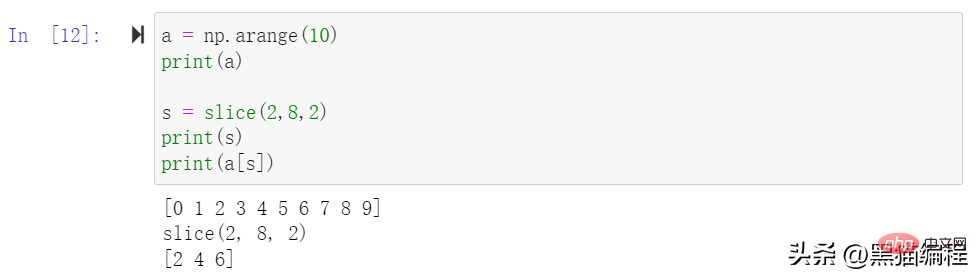
スライスには楕円を含めることもできます...、選択タプルの長さを配列の次元と同じにします。省略記号が行位置で使用されている場合、行内の要素を含む ndarray が返されます。

#高度なインデックス

整数配列インデックス

次の例では、配列を取得します。 # 位置 ##(0,0)、(1,1)

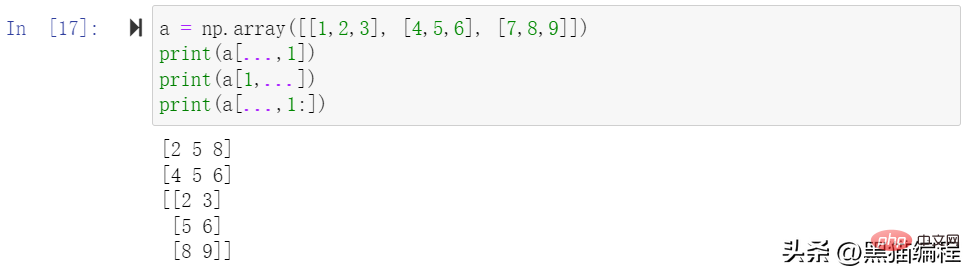
、および (2,0) の要素。

#

a = np.array([[0,1,2], [3,4,5], [6,7,8], [9,10,11]])
print(a)
print('-' * 20)

rows = np.array([[0,0], [3,3]])
cols = np.array([[0,2], [0,2]])

b = a[rows, cols]
print(b)
print('-' * 20)

rows = np.array([[0,1], [2,3]])
cols = np.array([[0,2], [0,2]])
c = a[rows, cols]
print(c)
print('-' * 20)

rows = np.array([[0,1,2], [1,2,3], [1,2,3]])
cols = np.array([[0,1,2], [0,1,2], [0,1,2]])
d = a[rows, cols]
print(d)

[[ 012]
 [ 345]
 [ 678]
 [ 9 10 11]]
--------------------
[[ 02]
 [ 9 11]]
--------------------
[[ 05]
 [ 6 11]]
--------------------
[[ 048]
 [ 37 11]
 [ 37 11]]

返される結果は、各コーナー要素を含む ndarray オブジェクトです。

スライスを使用してインデックス配列と組み合わせることができます: または ....次の例のように:

a = np.array([[1,2,3], [4,5,6], [7,8,9]])

print(a)
print('-' * 20)

b = a[1:3, 1:3]
print(b)
print('-' * 20)

c = a[1:3, [0,2]]
print(c)
print('-' * 20)

d = a[..., 1:]
print(d)

[[1 2 3]
 [4 5 6]
 [7 8 9]]
--------------------
[[5 6]
 [8 9]]
--------------------
[[4 6]
 [7 9]]
--------------------
[[2 3]
 [5 6]
 [8 9]]

ブール型インデックス

ブール型配列を使用してターゲット配列にインデックスを付けることができます。

ブール インデックスは、ブール演算 (比較演算子など) を使用して、指定された条件を満たす要素の配列を取得します。

次の例では、5 より大きい要素を取得します。

a = np.array([[1,2,3], [4,5,6], [7,8,9]])

print(a)
print('-' * 20)

print(a[a > 5])

[[1 2 3]
 [4 5 6]
 [7 8 9]]
--------------------
[6 7 8 9]

次の例では、~ (補数演算子) を使用して、 NaN をフィルターします。

a = np.array([np.nan, 1, 2, np.nan, 3, 4, 5])

print(a)
print('-' * 20)

print(a[~np.isnan(a)])

[nan1.2. nan3.4.5.]
--------------------
[1. 2. 3. 4. 5.]

次の例は、配列から複数以外の要素をフィルターで除外する方法を示しています。

a = np.array([1, 3+4j, 5, 6+7j])

print(a)
print('-' * 20)

print(a[np.iscomplex(a)])

[1.+0.j 3.+4.j 5.+0.j 6.+7.j]
--------------------
[3.+4.j 6.+7.j]

ファンシー インデックス

ファンシー インデックスとは、インデックス付けに整数配列を使用することを指します。

Fancy インデックスは、インデックス配列の値に基づく値をターゲット配列の軸の添字として受け取ります。

1 次元の整数配列をインデックスとして使用する場合、ターゲットが 1 次元配列の場合、インデックスの結果は対応する位置の要素になります。次元配列の場合、それは添字に対応する行です。

Fancy インデックス作成はスライスとは異なり、常にデータを新しい配列にコピーします。

#1 次元配列

#

a = np.arange(2, 10)

print(a)
print('-' * 20)

b = a[[0,6]]
print(b)

[2 3 4 5 6 7 8 9]
--------------------
[2 8]

#2 次元配列

# #1、順次インデックス配列を渡します

a = np.arange(32).reshape(8, 4)

print(a)
print('-' * 20)

print(a[[4, 2, 1, 7]])

[[ 0123]
 [ 4567]
 [ 89 10 11]
 [12 13 14 15]
 [16 17 18 19]
 [20 21 22 23]
 [24 25 26 27]
 [28 29 30 31]]
--------------------
[[16 17 18 19]
 [ 89 10 11]
 [ 4567]
 [28 29 30 31]]

2、逆順のインデックス配列

a = np.arange(32).reshape(8, 4)
print(a[[-4, -2, -1, -7]])

[[16 17 18 19]
 [24 25 26 27]
 [28 29 30 31]
 [ 4567]]

を渡します

3. 複数のインデックス配列を渡す (np.ix_ を使用する必要があります)

np.ix_ 関数は、2 つの配列を入力し、デカルト積マッピング関係を生成することです。

デカルト積とは、数学における 2 つのセット X と Y のデカルト積 (デカルト積) を指し、直積とも呼ばれ、

X×Y# # で表されます。 #、最初のオブジェクトは X のメンバーであり、2 番目のオブジェクトは Y のすべての可能な順序ペアのメンバーの 1 つです。

たとえば、A={a,b}、B={0,1,2} の場合、

A×B={(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}
B×A={(0, a), (0, b), (1, a), (1, b), (2, a), (2, b)}

a = np.arange(32).reshape(8, 4)
print(a[np.ix_([1,5,7,2], [0,3,1,2])])

[[ 4756]
 [20 23 21 22]
 [28 31 29 30]
 [ 8 119 10]]

Broadcast(Broadcast)

ブロードキャストは、さまざまな形状の配列に対して数値計算を実行する numpy の方法です。配列に対する算術演算は通常、対応する要素に対して実行されます。

如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同，且各维度的长度相同。

a = np.arange(1, 5)
b = np.arange(1, 5)

c = a * b
print(c)

[ 149 16]

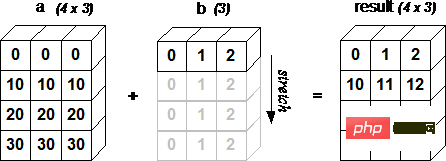
当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制。如：

a = np.array([
[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]
])

b = np.array([0, 1, 2])

print(a + b)

[[ 012]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

下面的图片展示了数组 b 如何通过广播来与数组 a 兼容。

tile扩展数组

a = np.array([1, 2])

b = np.tile(a, (6, 1))
print(b)

print('-' * 20)

c = np.tile(a, (2, 3))
print(c)

[[1 2]
 [1 2]
 [1 2]
 [1 2]
 [1 2]
 [1 2]]
--------------------
[[1 2 1 2 1 2]
 [1 2 1 2 1 2]]

4x3 的二维数组与长为 3 的一维数组相加，等效于把数组 b 在二维上重复 4 次再运算：

a = np.array([
[0, 0, 0],
[10, 10, 10],
[20, 20, 20],
[30, 30, 30]
])

b = np.array([0, 1, 2])
bb = np.tile(b, (4, 1))

print(a + bb)

[[ 012]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

广播的规则:

• 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分都通过在前面加 1 维补齐。
• 输出数组的形状是输入数组形状的各个维度上的最大值。
• 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错。
• 当输入数组的某个维度的长度为 1 时，沿着此维度运算时都用此维度上的第一组值。

简单理解：对两个数组，分别比较他们的每一个维度（若其中一个数组没有当前维度则忽略），满足：

• 数组拥有相同形状。
• 当前维度的值相等。
• 当前维度的值有一个是 1。

若条件不满足，抛出 "ValueError: frames are not aligned" 异常。

以上がPythonデータ分析モジュールNumpyのスライス、インデックス作成、ブロードキャストについて詳しく解説の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。