拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にします
最近、AIペイントがとても人気があります。
AI の描画機能に驚嘆する一方で、拡散モデルが AI において大きな役割を果たしているということはご存じないかもしれません。人気モデルOpenAIのDALL・E 2を例に挙げると、簡単なテキスト(プロンプト)を入力するだけで、1024*1024の高解像度画像を複数生成できます。
DALL・E 2 が発表されて間もなく、Google は、指定されたテキストの説明からシーンのリアルな画像を生成できるテキストから画像への AI モデルである Imagen をリリースしました。 。
ほんの数日前、Stability.Ai はテキスト生成画像モデル Stable Diffusion の最新バージョンを公開し、生成された画像は商用グレードに達しました。
Google が 2020 年に DDPM をリリースして以来、普及モデルは徐々に発電分野で新たな注目のスポットになりました。その後、OpenAI が GLIDE や ADM-G モデルなどを発表し、普及モデルが普及しました。
多くの研究者は、拡散モデルに基づくテキスト画像生成モデルはパラメータが少ないだけでなく、より高品質な画像を生成し、GAN に代わる可能性があると考えています。
しかし、拡散モデルの背後にある数式は、VAE や GAN よりも理解するのがはるかに難しいと多くの研究者が信じており、多くの研究者を落胆させています。
最近、Google Research の研究者が「拡散モデルを理解する: 統一された視点」を執筆しました。この記事では、拡散モデルの背後にある数学的原理を非常に詳細に示しており、他の人にも理解してもらえるようにすることを目的としています。研究者は、拡散モデルとは何か、そしてそれがどのように機能するのかを追跡して学ぶことができます。 
論文アドレス: https://arxiv.org/pdf/2208.11970.pdf この論文がどれほど「数学的」であるかについて、論文の著者は次のように述べています。それは次のようになります: これらのモデルの背後にある数学を、耐え難いほど詳細に示します。
この論文は 6 つの部分に分かれており、主に生成モデル、ELBO、VAE、階層型 VAE、変分拡散モデル、スコアベースの生成モデルなどが含まれます。

以下は、紹介用の論文からの抜粋です:
世代モデル
分布内の観測サンプル x が与えられた場合、生成モデルの目標は、その真のデータ分布 p(x) をモデル化する方法を学習することです。モデルが学習された後、新しいサンプルを生成できます。さらに、いくつかの形式では、学習モデルを使用して観測値やサンプルデータを評価することもできます。
現在の研究文献には、いくつかの重要な方向性があります。この記事では、主に次のようなものを含む、高レベルで簡単に紹介するだけです: 複雑な分布のサンプリング プロセスをモデル化する GAN。 。 「尤度ベースの」手法とも呼ばれる生成モデルは、観察されたデータ サンプルに高い尤度を割り当てることができ、通常は自己回帰、正規化されたフロー、VAE を含みます。エネルギーベースのモデリング。このアプローチでは、分布は任意の柔軟なエネルギー関数として学習され、その後正規化されます。スコアベースの生成モデルでは、エネルギー関数自体をモデル化することを学習するのではなく、エネルギー モデルに基づくスコアがニューラル ネットワークとして学習されます。
この研究では、この論文で示されているように、拡散モデルには尤度ベースの解釈とスコアベースの解釈があることを調査してレビューします。
変分拡散モデル
簡単に見ると、変分拡散モデル (VDM) には 3 つの主要な制限された (または仮定された) マルコフがあると考えることができます。階層変分オートエンコーダ (MHVAE)、それらは次のとおりです:
- 潜在次元はデータ次元とまったく同じです;
- 各タイム ステップにおける潜在エンコーダーの構造は学習されず、事前定義されます線形ガウスモデルとして。言い換えれば、これは前のタイム ステップの出力を中心としたガウス分布です。
- #ポテンシャル エンコーダーのガウス パラメーターは時間の経過とともに変化し、ポテンシャル分布の基準は時間の経過とともに変化します。プロセスの最終時間ステップ T はガウス分布です。
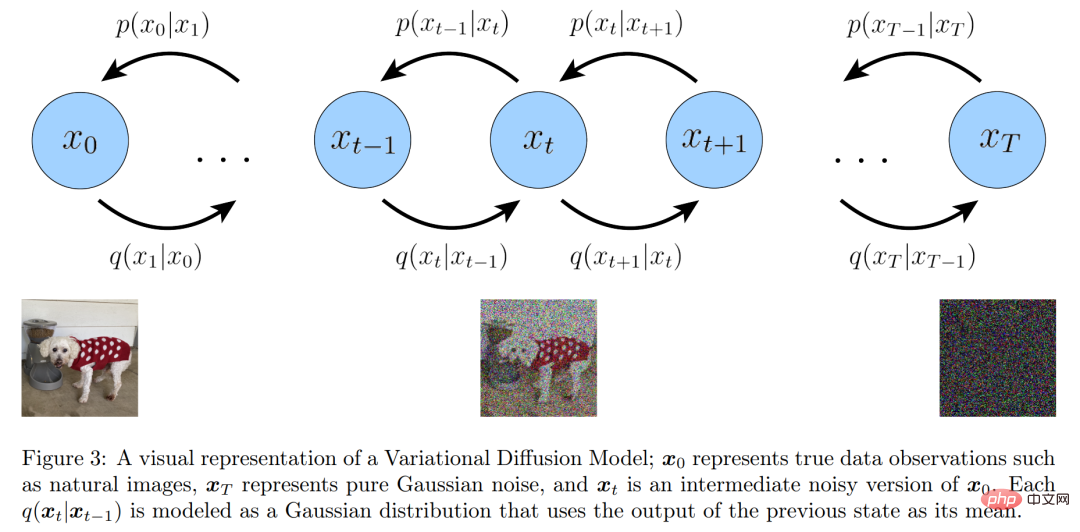
#変分拡散モデルの視覚的表現
さらに、標準マルコフ階層変分オートエンコーダーからの階層変換間のマルコフ プロパティを明示的に維持します。彼らは、上記の 3 つの主要な仮定の意味を 1 つずつ拡張しました。
最初の仮定から始めると、シンボルの誤用により、実データ サンプルと潜在変数は x_t として表現できるようになりました。ここで、t=0 は実サンプル データを表し、t ∈ [1 , T] は対応する潜在変数を表し、その階層構造は t によってインデックス付けされます。 VDM 事後分布は MHVAE 事後分布と同じですが、次のように書き換えることができます:

2 番目の仮説より, エンコーダーにおける各潜在変数の分布は、以前に層化された潜在変数を中心としたガウス分布であることが知られています。 MHVAE とは異なり、各タイム ステップでのエンコーダーの構造は学習されず、線形ガウス モデルとして固定されます。平均と標準偏差はハイパーパラメーターとして事前設定することも、パラメーターとして学習することもできます。数学的には、エンコーダ変換は次のように表されます。
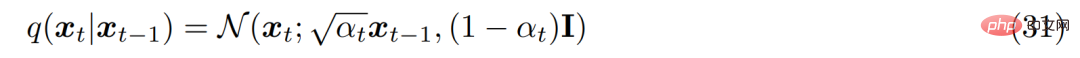
#3 番目の仮説の場合、α_t は固定されるか、次に従って学習可能です。取得されたスケジュールは時間の経過とともに進化するため、最終的な潜在変数 p(x_T) の分布は標準ガウス分布になります。その後、MHVAE の結合分布を更新でき、VDM の結合分布は次のように記述できます。一般に、この一連の仮定は、時間の経過とともに変化する画像の安定したノイズを説明します。研究者らは、ガウス ノイズを追加することで画像を徐々に破損させ、最終的にはガウス ノイズと同一になりました。
他の HVACE と同様に、VDM は証拠下限 (ELBO) を最大化することで最適化できます。これは次のように導出されます。 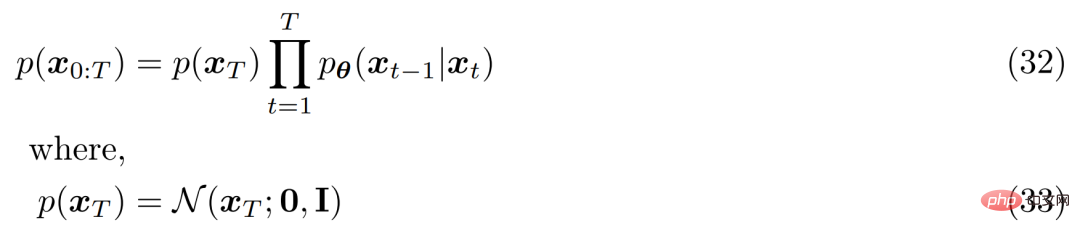
#ELBO の説明プロセスを以下の図 4 に示します。
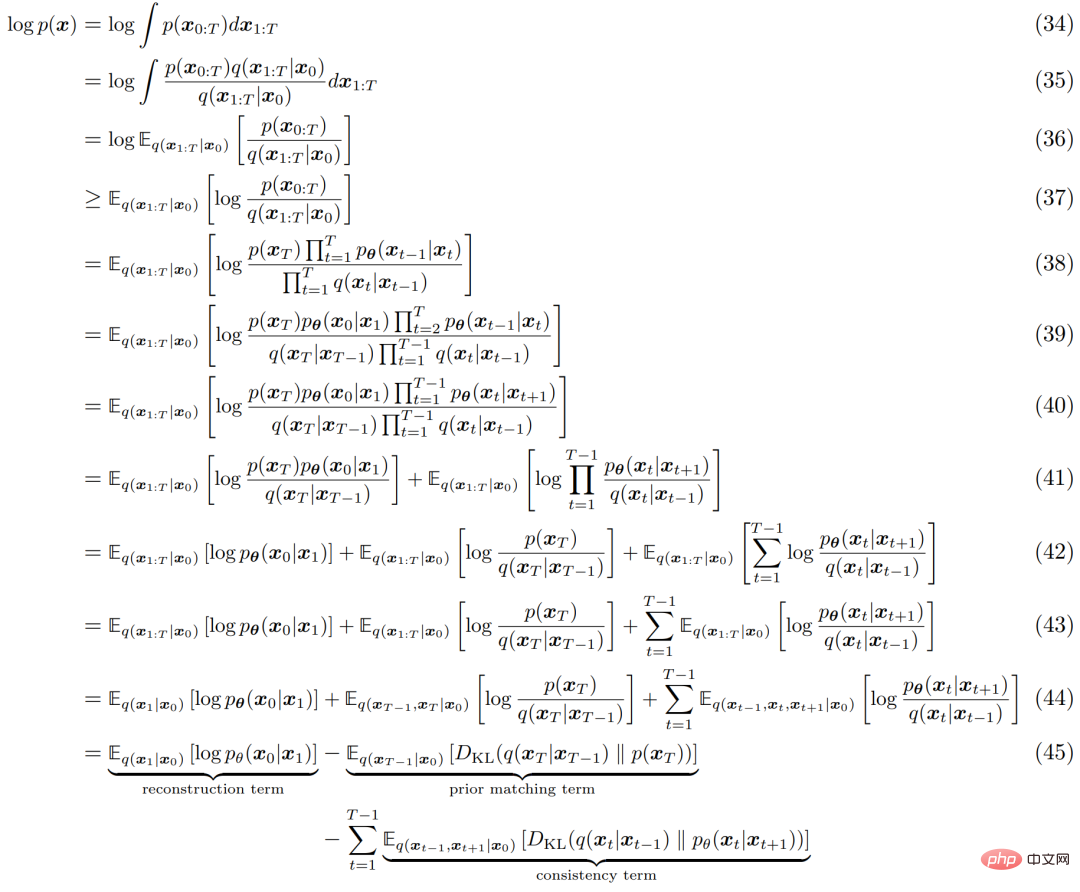 # #3 つの等価な説明
# #3 つの等価な説明
#前に示したように、変分拡散モデルは、任意のノイズのあるバージョン x_t とその時間インデックス t 自然画像 x_0 から元の x_t を予測するニューラル ネットワークを学習するだけでトレーニングできます。ただし、x_0 には同等のパラメータ化が 2 つあり、VDM のさらに 2 つの解釈を開発できます。
まず、大量のパラメータ化手法を使用できます。 q(x_t|x_0) の形式を導出する場合、式 69 は次のように整理できます。 これを、以前に導出された真のノイズ除去変換平均 µ_q(x_t, x_0) に取り込むと、次のように再導出できます。近似のノイズ除去変換平均 µ_θ(x_t, t) は次のように設定されます:
対応する最適化問題は次のようになります。 :
変分拡散モデルの 3 つの一般的な解釈を導き出すには、Tweedie の公式に目を向ける必要があります。これは、サンプルが与えられた場合、指数関数的家族分布の真の平均は、サンプルの最尤推定値 (経験的平均とも呼ばれる) に推定スコアを含む補正項を加えたものによって推定できることを指します。 数学的に言えば、ガウス変数 z 〜 N (z; µ_z, Σ_z) の場合、トゥイーディー公式は次のように表されます。 スコアベースの生成モデル 幸いなことに、この直感は、別のタイプの生成モデル、つまりスコアベースの生成モデルの助けを借りて得ることができます。実際、研究者らは、以前に導出された VDM 定式化が同等の分数ベースの生成モデリング定式化を持ち、2 つの解釈の間で柔軟な切り替えが可能であることを実証しました。 スコア関数の最適化がなぜ意味があるのかを理解するために、研究者らはエネルギーベースのモデルを再検討しました。任意の柔軟な確率分布は次のように記述できます。
正規化定数の計算またはモデル化を回避する方法。その方法は次のとおりです。ニューラル ネットワーク s_θ(x) を使用して、分布 p(x) のスコア関数 ∇ log p(x) を学習します。式 152 の両辺は対数微分できることがわかります:
# これはニューラル ネットワークとして自由に表現できます。 、正規化定数は含まれません。スコア関数は、トゥルー スコア関数を使用してフィッシャーの発散を最小限に抑えることで最適化できます。
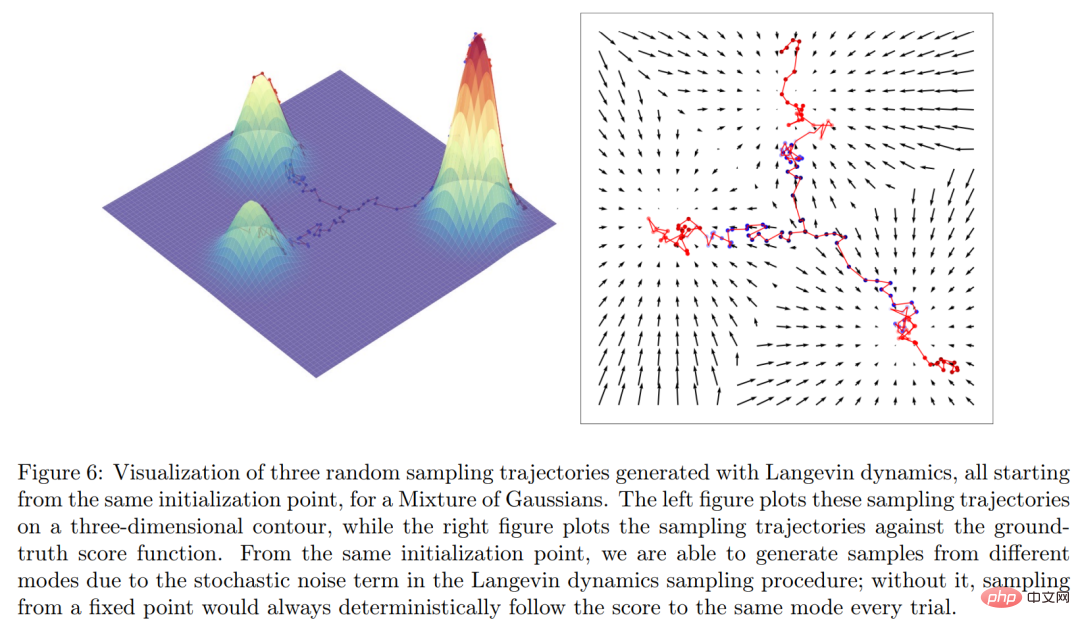
直観的に言えば、スコア関数はデータ x が位置する空間全体にわたるベクトル場を定義します。モデルは以下の図 6 に示されています。
最後に、研究者らは変分拡散モデルとスコアベースのモデル間の明示的な関係の生成を確立しました。 詳細については、元の論文を参照してください。 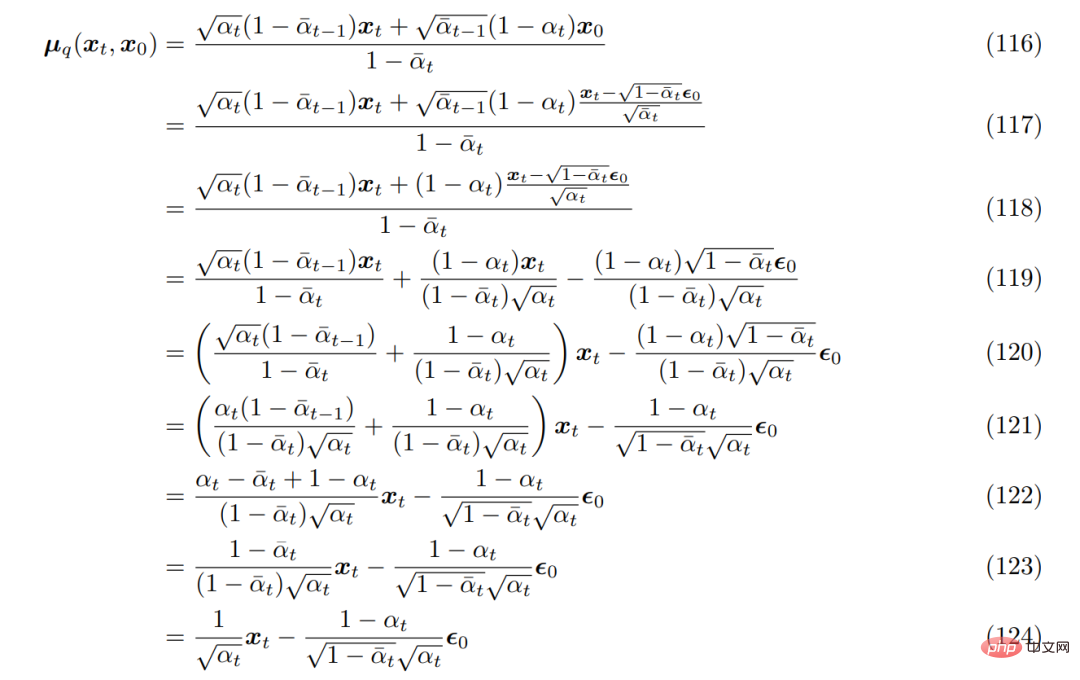
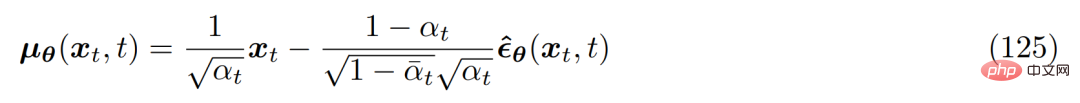
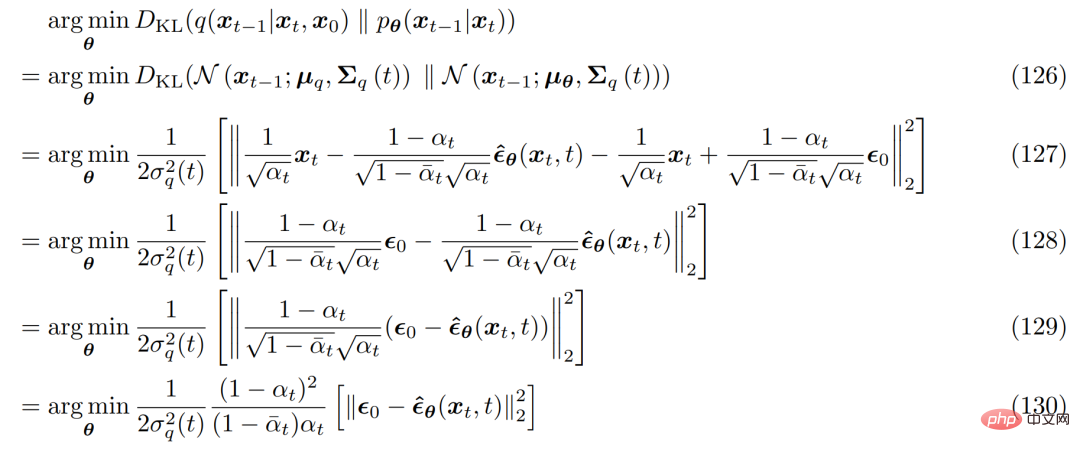
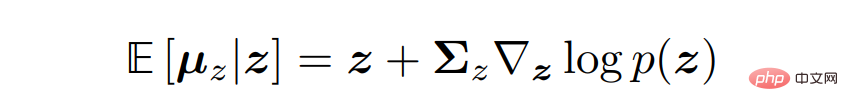 研究者らは、ニューラル ネットワークを最適化するだけで変分拡散モデルを学習できることを示しました。s_θ(x_t, t) が得られます。スコア関数 ∇ log p(x_t) を予測します。ただし、導出におけるスコア項は、Tweedie の公式の適用から得られます。これは、スコア関数が正確に何であるか、またはそれがモデル化する価値がある理由について、必ずしも優れた直観や洞察を提供するとは限りません。
研究者らは、ニューラル ネットワークを最適化するだけで変分拡散モデルを学習できることを示しました。s_θ(x_t, t) が得られます。スコア関数 ∇ log p(x_t) を予測します。ただし、導出におけるスコア項は、Tweedie の公式の適用から得られます。これは、スコア関数が正確に何であるか、またはそれがモデル化する価値がある理由について、必ずしも優れた直観や洞察を提供するとは限りません。 
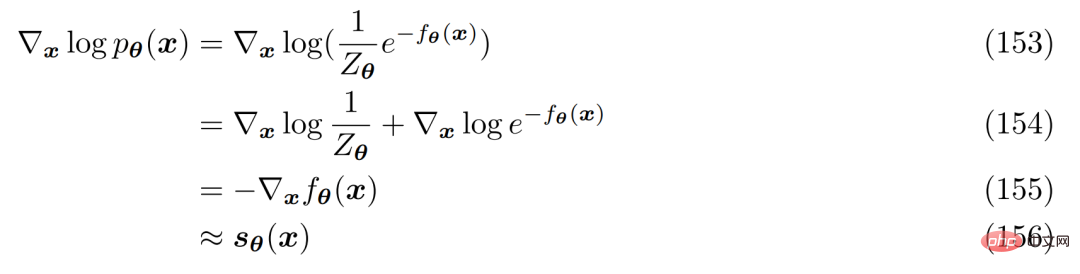

以上が拡散モデルの背後にある数学は難しすぎて理解しにくいですか? Google は統一された視点でそれを明確にしますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7467
7467
 15
15
 1376
1376
 52
52
 77
77
 11
11
 19
19
 20
20
 世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
世界で最も強力なオープンソース MoE モデルが登場。GPT-4 に匹敵する中国語機能を備え、価格は GPT-4-Turbo のわずか 1% 近くです
May 07, 2024 pm 04:13 PM
従来のコンピューティングを超える能力を備えているだけでなく、より低コストでより効率的なパフォーマンスを実現する人工知能モデルを想像してみてください。これは SF ではありません。世界で最も強力なオープンソース MoE モデルである DeepSeek-V2[1] が登場しました。 DeepSeek-V2 は、経済的なトレーニングと効率的な推論の特徴を備えた強力な専門家混合 (MoE) 言語モデルです。これは 236B のパラメータで構成されており、そのうち 21B は各マーカーをアクティブにするために使用されます。 DeepSeek67B と比較して、DeepSeek-V2 はパフォーマンスが優れていると同時に、トレーニング コストを 42.5% 節約し、KV キャッシュを 93.3% 削減し、最大生成スループットを 5.76 倍に高めます。 DeepSeek は一般的な人工知能を研究する会社です
 MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
MLP に代わる KAN は、オープンソース プロジェクトによって畳み込みまで拡張されました
Jun 01, 2024 pm 10:03 PM
今月初め、MIT やその他の機関の研究者らは、MLP に代わる非常に有望な代替案である KAN を提案しました。 KAN は、精度と解釈可能性の点で MLP よりも優れています。また、非常に少数のパラメーターを使用して、多数のパラメーターを使用して実行する MLP よりも優れたパフォーマンスを発揮できます。たとえば、著者らは、KAN を使用して、より小規模なネットワークと高度な自動化で DeepMind の結果を再現したと述べています。具体的には、DeepMind の MLP には約 300,000 個のパラメーターがありますが、KAN には約 200 個のパラメーターしかありません。 KAN は、MLP が普遍近似定理に基づいているのに対し、KAN はコルモゴロフ-アーノルド表現定理に基づいているのと同様に、強力な数学的基礎を持っています。以下の図に示すように、KAN は
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
こんにちは、電気アトラスです!ボストン・ダイナミクスのロボットが復活、180度の奇妙な動きにマスク氏も恐怖
Apr 18, 2024 pm 07:58 PM
Boston Dynamics Atlas は正式に電動ロボットの時代に突入します!昨日、油圧式アトラスが歴史の舞台から「涙ながらに」撤退したばかりですが、今日、ボストン・ダイナミクスは電動式アトラスが稼働することを発表しました。ボストン・ダイナミクス社は商用人型ロボットの分野でテスラ社と競争する決意を持っているようだ。新しいビデオが公開されてから、わずか 10 時間ですでに 100 万人以上が視聴しました。古い人が去り、新しい役割が現れるのは歴史的な必然です。今年が人型ロボットの爆発的な年であることは間違いありません。ネットユーザーは「ロボットの進歩により、今年の開会式は人間のように見え、人間よりもはるかに自由度が高い。しかし、これは本当にホラー映画ではないのか?」とコメントした。ビデオの冒頭では、アトラスは仰向けに見えるように地面に静かに横たわっています。次に続くのは驚くべきことです
 Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google は大喜び: JAX のパフォーマンスが Pytorch や TensorFlow を上回りました! GPU 推論トレーニングの最速の選択肢となる可能性があります
Apr 01, 2024 pm 07:46 PM
Google が推進する JAX のパフォーマンスは、最近のベンチマーク テストで Pytorch や TensorFlow のパフォーマンスを上回り、7 つの指標で 1 位にランクされました。また、テストは最高の JAX パフォーマンスを備えた TPU では行われませんでした。ただし、開発者の間では、依然として Tensorflow よりも Pytorch の方が人気があります。しかし、将来的には、おそらくより大規模なモデルが JAX プラットフォームに基づいてトレーニングされ、実行されるようになるでしょう。モデル 最近、Keras チームは、ネイティブ PyTorch 実装を使用して 3 つのバックエンド (TensorFlow、JAX、PyTorch) をベンチマークし、TensorFlow を使用して Keras2 をベンチマークしました。まず、主流のセットを選択します
 テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボットは工場で働く、マスク氏:手の自由度は今年22に達する!
May 06, 2024 pm 04:13 PM
テスラのロボット「オプティマス」の最新映像が公開され、すでに工場内で稼働可能となっている。通常の速度では、バッテリー(テスラの4680バッテリー)を次のように分類します:公式は、20倍の速度でどのように見えるかも公開しました - 小さな「ワークステーション」上で、ピッキング、ピッキング、ピッキング:今回は、それがリリースされたハイライトの1つビデオの内容は、オプティマスが工場内でこの作業を完全に自律的に行い、プロセス全体を通じて人間の介入なしに完了するというものです。そして、オプティマスの観点から見ると、自動エラー修正に重点を置いて、曲がったバッテリーを拾い上げたり配置したりすることもできます。オプティマスのハンドについては、NVIDIA の科学者ジム ファン氏が高く評価しました。オプティマスのハンドは、世界の 5 本指ロボットの 1 つです。最も器用。その手は触覚だけではありません
 FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: 魚眼カメラに基づいた最初のターゲット検出アルゴリズム
Apr 26, 2024 am 11:37 AM
目標検出は自動運転システムにおいて比較的成熟した問題であり、その中でも歩行者検出は最も初期に導入されたアルゴリズムの 1 つです。ほとんどの論文では非常に包括的な研究が行われています。ただし、サラウンドビューに魚眼カメラを使用した距離認識については、あまり研究されていません。放射状の歪みが大きいため、標準のバウンディング ボックス表現を魚眼カメラに実装するのは困難です。上記の説明を軽減するために、拡張バウンディング ボックス、楕円、および一般的な多角形の設計を極/角度表現に探索し、これらの表現を分析するためのインスタンス セグメンテーション mIOU メトリックを定義します。提案された多角形モデルの FisheyeDetNet は、他のモデルよりも優れたパフォーマンスを示し、同時に自動運転用の Valeo 魚眼カメラ データセットで 49.5% の mAP を達成しました。
 DualBEV: BEVFormer および BEVDet4D を大幅に上回る、本を開いてください!
Mar 21, 2024 pm 05:21 PM
DualBEV: BEVFormer および BEVDet4D を大幅に上回る、本を開いてください!
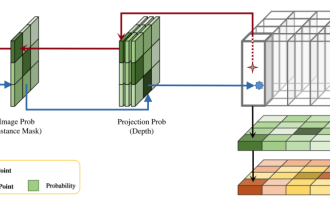
Mar 21, 2024 pm 05:21 PM
この論文では、自動運転においてさまざまな視野角 (遠近法や鳥瞰図など) から物体を正確に検出するという問題、特に、特徴を遠近法 (PV) 空間から鳥瞰図 (BEV) 空間に効果的に変換する方法について検討します。 Visual Transformation (VT) モジュールを介して実装されます。既存の手法は、2D から 3D への変換と 3D から 2D への変換という 2 つの戦略に大別されます。 2D から 3D への手法は、深さの確率を予測することで高密度の 2D フィーチャを改善しますが、特に遠方の領域では、深さ予測に固有の不確実性により不正確さが生じる可能性があります。 3D から 2D への方法では通常、3D クエリを使用して 2D フィーチャをサンプリングし、Transformer を通じて 3D と 2D フィーチャ間の対応のアテンション ウェイトを学習します。これにより、計算時間と展開時間が増加します。




