
"重み付き有向グラフ G=(V,E) では、各辺の重みは実数です。さらに、ソースと呼ばれる V の頂点も与えられます。
ソースから他のすべての頂点までの最短パス長を計算します。これは単一ソース最短パス (SSSP) 問題です。"
半世紀以上にわたり、世界中の研究者がこの問題の解決に努めてきました。このアルゴリズム パズルは、コペンハーゲン大学コンピューター サイエンス学部の研究チームによってついに解決されました。
負の重み SSSP アルゴリズム: 高速かつ効率的

論文リンク: https://arxiv。 org/abs/2203.03456
研究者のクリスチャン・ウルフ・ニルセン氏はインタビューで、彼らのソリューションは 30 年以上存在してきた最初の画期的な進歩であると述べました。 Õ(n(4/3) log W) 負の重みを備えた演算時間制約付き SSSP 組み合わせアルゴリズム。
SSSP には、ダイクストラ アルゴリズム (ダイクストラ アルゴリズム) とベルマン フォード アルゴリズム (ベルマン フォード アルゴリズム) の 2 つの古典的なアルゴリズムがあり、どちらも独自の制限があります。 。
ダイクストラ アルゴリズムは演算時間が最も短く、ほぼ線形時間に達します OO(m n log n) ですが、負の重みエッジは計算できません。
Bellman-Ford アルゴリズムは負の重みエッジを計算できますが、演算時間が長すぎて OO(mn に達します) )。現在、負の重み付けエッジを解決するための最先端の SSSP アルゴリズムは、複雑な連続最適化と動的代数およびグラフィカル アルゴリズムに依存しています。これは、後の世代の学者がアルゴリズムの最適化を続けたとしても、その計算時間は依然として Õ(n(4/3) log W## かかるという事実につながります。 #)。この計算時間の制約は 30 年前から存在しています。
これらの制限に直面して、Wulff-Nilsen は 2 つの質問を提起しました。
# 1) できること負の重み付けエッジ アルゴリズムの動作により、ほぼ線形な時間が達成されますか?
#2) これは簡単なツールで実現できますか?
#時間と品質の両方を必要とする方法はありますか?
#言わないでください、それは実際に存在します。
Wulff-Nilsen によって提案されたアルゴリズムは、単純な画像分解アルゴリズムである Low Diameter Decomposition によって強化された画像スケーリング アルゴリズムです。通常、この分解アルゴリズムは、非負の重み付けエッジのグラフ分解にのみ使用されます。この研究の貢献の 1 つは、それを負の重み付けエッジ画像に適用して、負の重み付けエッジ SSSP 再帰スケーリング アルゴリズムを強化することです。
導出プロセスWulff-Nilsen は、ジョンソンの価格アルゴリズムに基づいています。提案: 画像 G = (V, E, w) において、Φ を任意の関数とする: V→ Z。 w(Φ) を重み関数とします: #########意味: ###############、 ###: ###############。
画像内G = (V, E,w) および画像G' = (V, E,w')、次の場合: 1) 画像 G と画像間の最短距離image G' 内の最短距離は等しい、またはその逆; 2) G は G' 内にのみ存在します。 に負のウェイト リングが含まれる場合、イメージ G はイメージ G' と等しくなります。 系 2.7 任意の画像 と価格関数 Φ を考えます。 #####。 u では、v ∈ V、
です。 そして、どのリングでも C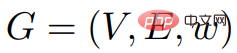 、。 したがって、
、。 したがって、
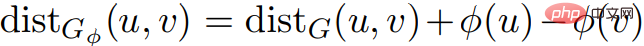 G は と等しくなります。
G は と等しくなります。
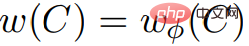 ##、、 の場合、G および
##、、 の場合、G および 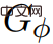 G'等しい。
G'等しい。 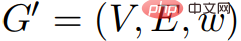
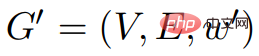
 このアルゴリズムの目的は、次の場合に価格関数 Φ を計算することです。 ##GΦ のすべてのエッジの重みは、負の重みサイクルが存在しないと仮定すると、負ではありません。その後、
このアルゴリズムの目的は、次の場合に価格関数 Φ を計算することです。 ##GΦ のすべてのエッジの重みは、負の重みサイクルが存在しないと仮定すると、負ではありません。その後、
でダイクストラのアルゴリズムを実行できます。 #その後、Wulff-Nilsen はアルゴリズム フレームワークの導入を開始しました。 まず、Wulff-Nilsen は、負の重みエッジのないグラフを入力するアルゴリズム Dijkstra (G,s) があると仮定しますG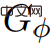 , 頂点 s ∈ V, s in
, 頂点 s ∈ V, s in
は最短パス ツリーを出力します。実行時間は #O(m
n log n) です。 G が DAG (有向非巡回グラフ) の場合、 が次のような価格関数 #単一ソース最短パス問題の目的は、特定の開始ノードからネットワーク内の他のすべてのノードまでの最短パスを見つけることです。 #ネットワークは、ノードとエッジと呼ばれるノード間の接続で構成されるグラフとして表されます。 各エッジには方向 (たとえば、これは一方通行の道路を表すために使用できます) と、それに沿って移動するコストを表す重みがあります。角。すべてのエッジの重みが負でない場合、問題は古典的なダイクストラのアルゴリズムを使用してほぼ線形時間で解決できます。 新しい結果は、ダイクストラのアルゴリズムとほぼ同じ時間でこの問題を解決しますが、負のエッジの重みも考慮します。 その後、Wulff-Nilsen 氏は、組み合わせツールで最も重要な 2 つのアルゴリズム、 ScaleDown と SPmain について言及しました。 ScaleDown アルゴリズムは段階的に実行され、最後の段階では ElimNeg () を使用して価格を計算します。関数番号 について、 が条件を満たすことを意味します ( であるため)。これは、ScaleDown 出力が正しいことを証明します。 アルゴリズムが終了した場合、すべての これは、すべての 、 理論が に当てはまると仮定した帰納法により、 # したがって、 したがって、 #これにより、SPmain アルゴリズムの正しさを証明できます。 これまでのところ、Wulff-Nilsen の負の重み SSSP ソリューションの 2 つの最も重要なアルゴリズムが正しいことが証明されています。新しいアルゴリズムは、ほぼ線形の時間を確保しながら、負の重みを導入することに成功しました。 昨年、ウルフ・ニルセンは、時間とともに変化するネットワーク内で最短パスを見つける方法を含む、同じ分野で新たな進歩を遂げました。最近の謎に対する彼の解決策は、この研究に基づいています。 彼は、SSSP 問題を解決することで、電気自動車が目的地までの最速ルートを瞬時に計算できるだけでなく、これを行うための最もエネルギー効率の高い方法です。 Wulff-Nilsen 氏は次のように説明しました。「私たちのアルゴリズムは負の重みを追加します。これは、以前のアルゴリズムにはなかった次元です。実際の例は、山での運転時です。負の重量の次元を使用すると、ナビゲーション システムは電気自動車の所有者に下り坂の多いルートを推奨できるため、下り坂で電気自動車を充電できるようになります。」 Wulff-Nilsen 氏はまた、自社のアルゴリズムは電気自動車のルート計画だけでなく、金融業界の投機の監視にも使用できると述べた。同氏は、「原則として、このアルゴリズムは、中央銀行などのユーザーに早期警告を提供したり、さまざまな通貨の売買で投機を行う投機家に警告したりするために使用できます。現在、多くの犯罪者が犯罪を行うためにコンピューターを使用していますが、私たちのアルゴリズムは非常に高速なので、可能性があります。脆弱性が悪用される前に監視し、検出するために使用されます。」 ダイクストラが最初に最短距離問題を提案したのは 1959 年でした。 , 彼はおそらく思いつかなかったでしょう。 , 60 年以上にわたり、この問題の解決策を絶えず最適化している人たちがいます。また、パズルの答えがこれほど豊かな含意を持っていることに驚かれるかもしれません。 #これが科学の魅力なのかもしれません。 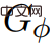 Φ を計算します。負のエッジの重みは単純です。トポロジの v1、...、vn をループし、すべての入力エッジの重みが負でないように Φ(vi) を設定するだけです。
Φ を計算します。負のエッジの重みは単純です。トポロジの v1、...、vn をループし、すべての入力エッジの重みが負でないように Φ(vi) を設定するだけです。 
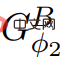 ##Φ2。 ElimNeg が終了すると、価格関数 ψ'、letすべてのエッジ値が返されます。は負ではありません。つまり、
##Φ2。 ElimNeg が終了すると、価格関数 ψ'、letすべてのエッジ値が返されます。は負ではありません。つまり、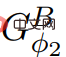 、、
、、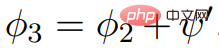 には負の重みが含まれていないためです。
には負の重みが含まれていないためです。 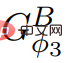
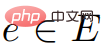
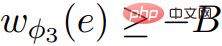
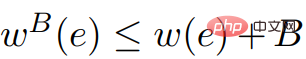
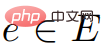 および
および 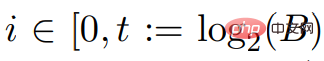 について、
について、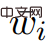 は整数であり、すべての # について##、
は整数であり、すべての # について##、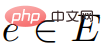 。
。 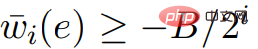
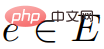 について意味します。
について意味します。 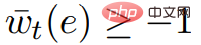 したがって、グラフ G* の重みは負ではありません。
したがって、グラフ G* の重みは負ではありません。 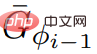 5 行目の ScaleDown に対する応答アルゴリズムの
5 行目の ScaleDown に対する応答アルゴリズムの 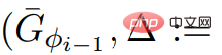
 # の呼び出しは、必要な入力属性を満たします。
# の呼び出しは、必要な入力属性を満たします。 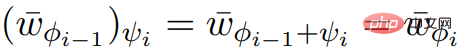 の出力と ScaleDown を通じて、## を取得できます。 #。
の出力と ScaleDown を通じて、## を取得できます。 #。 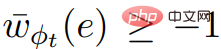 なので、if C は
なので、if C は 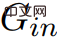
 # の の値はすべて 2n の倍数であるため、負の重みサイクル、および
# の の値はすべて 2n の倍数であるため、負の重みサイクル、および 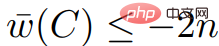 ; も
; も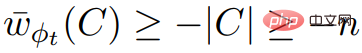 、 はわかっているので、
、 はわかっているので、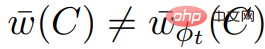 は系 2.7 と矛盾します。
は系 2.7 と矛盾します。 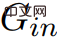 に負の重みサイクルが含まれている場合、アルゴリズムは終了しないと結論付けることができます。 。
に負の重みサイクルが含まれている場合、アルゴリズムは終了しないと結論付けることができます。 。
以上が60年前のパズル!コペンハーゲン大学の研究者が「単一ソースの最短経路」問題を解決の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。