
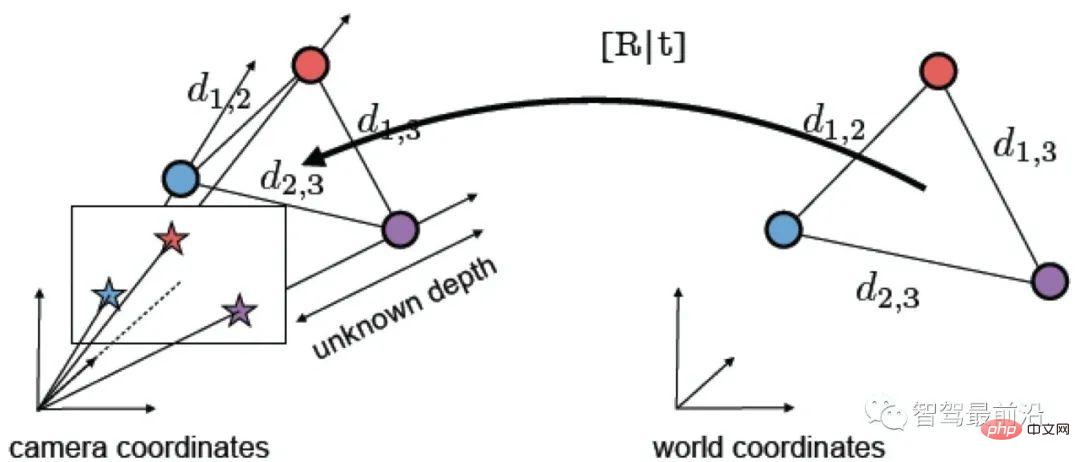
無人運転では、知覚、位置決め、計画と意思決定、および制御が 4 つの基本的なシステム モジュールです。現在のアルゴリズムでは絶対的なインテリジェンスを実現できないため、安全な自動運転を実現するためにモジュールのパフォーマンスと堅牢性を向上させるには、依然として大量の事前知識が必要です。中でも高精度地図は、道路や周辺環境に関する事前知識を統合したものです。地図に基づく正確な位置情報は、走行状況を判断するための重要な基礎となり、その後の認識や計画の決定を強力にサポートします。
現在、測位に使用される主なデータ ソースには、GPS、LIDAR、ビジョン、ミリ波レーダーが含まれます。視覚に関しては、現在、業界で十分に信頼できる測位ソリューションが認識されていませんが、この分野での探究は決して止まらず、その主な理由は次のとおりです:
安全性が最も重要な指標自動運転システムのほとんどの機能の実装は、マルチソース データとさまざまなアルゴリズム結果の結合です。完璧なセンサー ソリューションはありません。たとえば、広く使用されているソリューションである GPS RTK は、衛星の状態、気象条件、データ リンクの伝送状態の影響を受けやすく、トンネル、屋内、および高濃度の人口密集地域では使用できません。建物が立ち上がる。さらに、LIDAR には、深度情報を提供するための計算負荷が小さく、照明の影響を受けないという利点がありますが、情報はまばらで、コストは依然として非常に高価であり、大量の車両を組み立てる能力はまだありません。それに比べて、カメラから提供される視覚情報は照明や天候の影響を受けますが、低コストでコンテンツが豊富であるため、現在の運転支援ソリューションの主要なデータソースであり、地図測位においても大きな可能性を秘めています。
主流の視覚測位アルゴリズムの中心的な考え方は同じであるため、この記事では、一連の重要なアルゴリズムの観点から、実際に最も一般的に使用されている特徴点に基づく全地球測位のみを紹介します。フレームワーク コンポーネント アルゴリズム、つまり地図座標系での位置決め。この記事では、位置決めアルゴリズムをマクロ的に入門することを目的として、最適化や幾何拘束式の導出については省略していますので、詳細については関連文献や書籍を参照してください。
ビジュアル グローバル ポジショニングとは、マップ座標系でカメラの位置を見つけることを指します。現在の画像 6 自由度 (DoF) ポーズ (Pose)、つまり (x、y、z) 座標、および 3 つの座標軸 (ヨー、ピッチ、ロール) の周りの角度偏向。現在、主に 3D 構造ベースの方法、2D 画像ベースの方法、シーケンス画像ベースの方法、深層学習ベースの方法に分類できます。このうち、深層学習に基づく手法はエンドツーエンド手法であり、他の多段階(マルチステージ)の非エンドツーエンド手法はプロセスが異なりますが、アルゴリズムの考え方はほぼ図1のとおりです。表示:

#図 1: クエリ画像に基づいて 2D-3D 変換行列を計算し、カメラのポーズを解決します
構築されたマップに基づいて、履歴内で最も類似したマップ サブセット (画像/点群/特徴点) と一致し、一致したマップ サブセットによって提供される履歴ポーズの真の値に基づいて、 , 特徴点座標の真の値、点ペア間の変換行列を計算し、現在のカメラのポーズを解決します。
つまり、そのコアには、画像の説明、マッピング クエリ、特徴のマッチング、ポーズの計算という 4 つの側面が含まれています。これは技術レベルでのマクロな分類にすぎず、実際のアルゴリズム フレームワークは必ずしもこの順序で実行されるわけではなく、学者は主にこれらの技術の改良に重点を置いて研究を行っています。全体として、特徴点に基づく画像記述は基本的に成熟しており、発展性は低い。姿勢計算は幾何学的制約に基づいた最適化問題であるため、方法は比較的固定されています。対照的に、マッピング クエリとフィーチャ マッチングには多くの改良された技術があります。データ ソースに応じて、マッピング クエリとマッチングは 2D-2D、2D-3D、または 3D-3D になります。 2D 画像はカメラで取得され、3D 点群は深度を提供する双眼カメラまたは RGB-D カメラで生成できます。
2D画像自体は明るさと色から構成されるマトリックスであり、見る角度、照明、色合いの変化などに非常に敏感です。そしてそれを直接使用することは非常に困難です。したがって、関連する計算には通常、代表点が使用されます。人々は、そのような点に回転、平行移動、スケール、照明の不変性などの利点があることを期待しています。これらの点は、キーポイントや記述子を含め、画像の特徴点と呼ばれます。キー ポイントは特徴点の位置を表現し、記述子は特徴点の視覚的特徴を主にベクトル形式で記述します。一般に、記述子は主に、特定のパターンのキーポイント付近のグレースケール/カラー グラデーションの変化をカウントします。堅牢な記述子の場合、同じ特徴点の記述子の距離 (Distance) は、異なる画像の異なる状況ではより小さくなる必要があります。
記述子は通常、手動で作成された機能です。古典的な説明には、HOG (方向性勾配のヒストグラム) [1]、SIFT (スケール不変特徴変換) [2]、SURF (高速ロバスト特徴) [3]、AKAZE (Accelerated KAZE) [4] などが含まれます。
リアルタイム要件を満たすために、LBP (ローカル バイナリ パターン) [5]、BRIEF (バイナリ ロバスト) など、より高速な計算速度を備えたいくつかのバイナリ パターン記述子が設計されています。独立した基本特徴)、ORB (Oriented FAST および回転 BRIEF) [6]、BRISK (Binary堅牢不変スケーラブル キーポイント) [7]、FREAK (Fast retina key-point) [8] など。
ディープ ラーニングが普及する前は、これらの手作りの機能がコンピューテーショナル ビジョン業界全体をリードしていました。現在に至るまで、これらの機能はラベル付きデータが不足しているシナリオで広く使用されています。多くの制約、アプリケーション。以下に、一般的に使用される 2 つの記述子を簡単に紹介します。
SIFT
SIFT 記述子は、CV の世界で最も影響力のあるテクノロジーの 1 つと見なされます。キーポイント検出の観点からは、マルチスケール空間上の極値点をキーポイントとして検出するために、主にガウス差分法 (DoG) が使用されます。 Babaud et al. [9] は、ガウス平滑化が使用できる唯一のマルチスケール空間平滑化フィルター カーネルであることを証明し、関連する方法に十分な理論的サポートを提供します。
では、なぜこのような方法で主要な特徴点を見つけることができるのでしょうか?
ガウス カーネルは、ぼかした空間を通じて画像をさまざまなスケールに拡大縮小できるため、一方、勾配の変化が小さい滑らかな領域では、異なるスケール空間での値の差が小さくなります。逆に、エッジ、ポイント、コーナー、テクスチャなどの領域では差が大きくなります。このように、隣接するスケールの画像間で差分をとることにより、最終的にマルチスケール空間の極点を計算することができる。ただし、画像の詳細が異なると、本質的に縮尺も異なります。たとえば、ポートレートでは、小さなぼかしの後に顔が滑らかになって 1 つのピースになる場合がありますが、フレームの隅では局所的な「極端な値」を反映するために大規模なスムージングが必要になる場合があります。
したがって、図 2 に示すように、まず画像ピラミッドを使用して画像をグループ化 (オクターブ) し、次に異なるスケールのガウス カーネルを各グループで使用してシリーズを形成します。層の。この方法は、単により多くのスケールのガウス カーネルを使用するよりも優れており、より多くの特徴点を検出できます。 SIFT はキーポイント検出に DoG を使用しますが、他の検出方法も実行可能であり、SIFT 記述子の確立に影響を与えないことに注意してください。
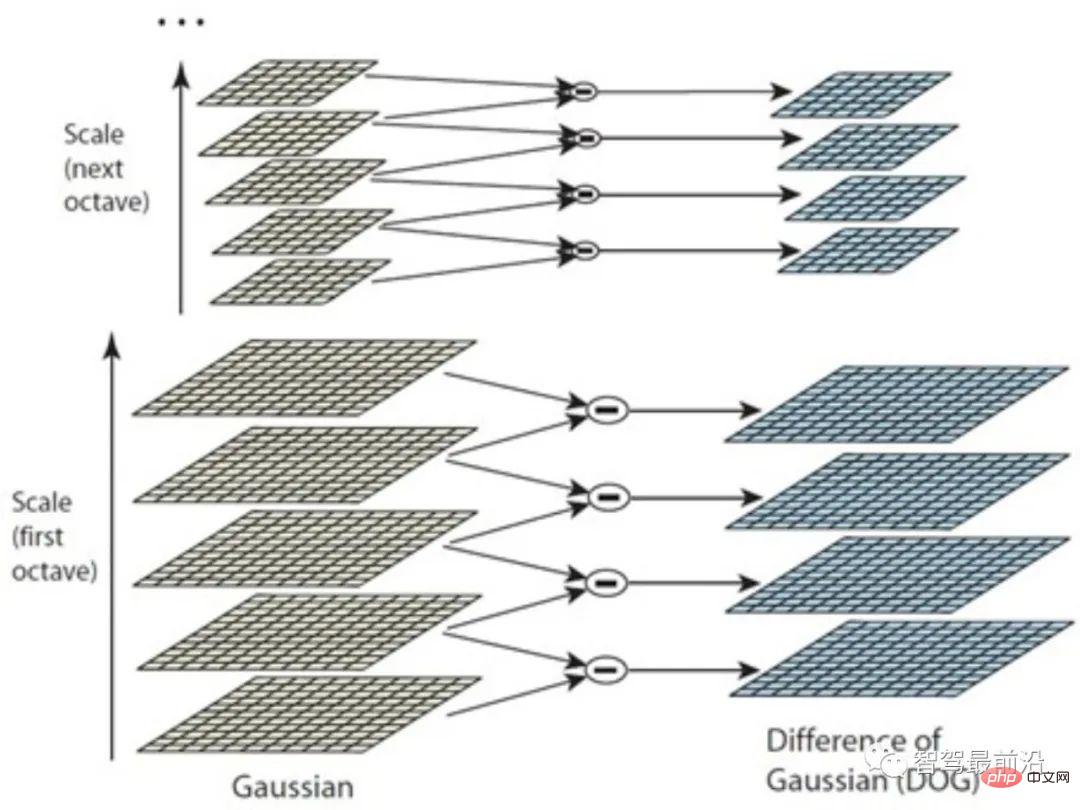
図 2: ガウス法の違い
SIFT 機能の説明Points sub は、HOG の単純な統計バージョンとして理解できます。図3に示すように、検出されたキーポイントを中心として周囲の16×16の領域を選択し、その領域を4つの4×4のパッチに再構成します。各ブロックについて、8 ビンのヒストグラムを使用して勾配がカウントされます。勾配の方向によって、どのビンに該当するかが決まり、勾配のモジュールによって値のサイズが決まります。スケールの一貫性を確保するには、グラデーション サイズを正規化する必要があります。回転の不変性を確保するために、16 × 16 領域内のすべての勾配に基づいて主方向が計算され、すべての勾配が主方向に従って回転されます。結果は、4 × 4 × 8 の 128 次元ベクトルになります。
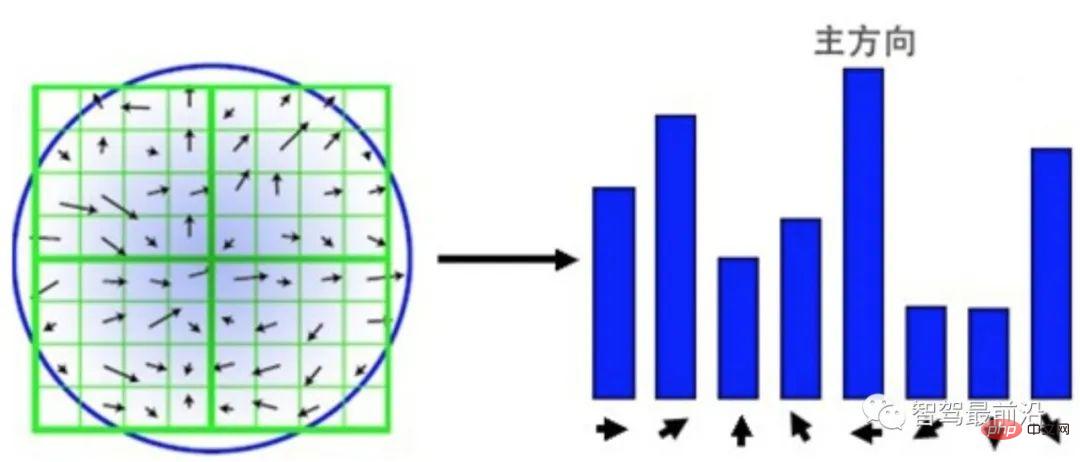
#図 3: 勾配ブロック統計に基づく SIFT 記述子
##バイナリ記述子
SIFT が提案された後、SURF、AKAZE などのいくつかの改良されたアルゴリズムが作成されましたが、2019 年の今日でも、一部のシナリオではアルゴリズムのリアルタイム要件を保証することが依然として困難です。たとえば、ハンドヘルド デバイスの計算能力には一般に限界があります。自動運転では、複数のコンピューティング集約型モジュールによって CPU と GPU リソースを同時にスケジュールする必要があります。したがって、効率はアルゴリズムの実用性を検討するための重要な指標です。
効率を向上させるために、学者によっていくつかのバイナリ記述子が提案されています。一般に、これらの方法では、フィーチャのキー ポイントの周囲でポイント サンプリングが実行されます。次に、一対の点のグレースケール サイズが比較され、その結果が 0/1 で表され、N 次元のバイナリ記述ベクトルが形成され、特徴点のバイナリ パターンが形成されます。異なるバイナリ記述子の最大の違いは、主に、異なる特徴サンプリング モードと異なる点ペア選択方法にあります。
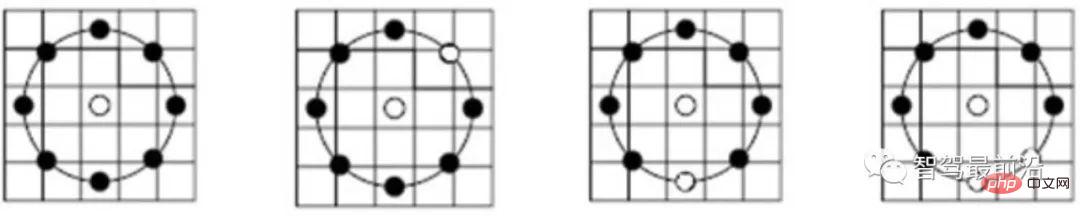
#図 4: LBP 記述サブサンプリング モード
図に示すように4 に示すように、LBP 記述子はキー ポイントの周囲を循環サンプリングし、それを中央のキー ポイントのグレースケールと比較するスキームを採用しています。グレースケールの比較結果がリング上に表示され、黒い点が 0、白い点が 1 になります。 LBP はバイナリ記述子の最も単純な形式ですが、ORB は BRIEF 機能を改良し、現在一般的に使用されているバイナリ記述子です。図 5 に示すように、点のペアを選択するとき、ORB は単に中心点を使用するのとは異なり、ランダムな方法を使用して局所的な詳細をより包括的に記述します。ただし、点ペア間の相関は比較的大きく、そのため記述子の識別性が低下します。 ORB は、貪欲かつ網羅的な手法を直接使用してこの問題を解決し、相関の低いランダムな点のペアを見つけます。
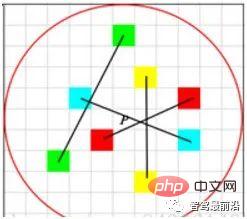
図 5: ORB 記述子ポイント ペア選択モード##上記のサンプリングバイナリ記述子の方法と点ペア選択方法は人々の一般的な直感と一致していますが、BRISK や FREAK などの記述子は、スケール情報を備えたより規則的なバイナリ パターン構築方法を提供します。たとえば、FREAK 記述子は人間の目の視覚サンプリング パターンを模倣します。図6に示すように、各サンプリング点の値は赤い円内の平均グレー値であり、青い線は点ペアの選択計画を表します。
 図 6: FREAK はサブサンプリング、ポイント ペア選択モードについて説明します。
図 6: FREAK はサブサンプリング、ポイント ペア選択モードについて説明します。
#バイナリ記述子の高い効率は主に 3 つの側面に反映されます。
(1) バイナリ記述子は特徴記述としてバイナリ ベクトルを使用し、特定の勾配を計算せずに点ペアのサイズを比較するだけで済みます。
(2) ハミング距離 (ハミング距離) は、計算が速く、最適化が容易であり、2 つの記述子を比較するために使用できます。
(3) 各バイナリ ベクトルは 10 進数に対応するため、それ自体もパターンを表し、SIFT のようなヒストグラムで表す必要はありません。
バイナリ記述子は、通常、SIFT ファミリ記述子ほど識別力がありませんが、特定のシナリオでは、並列プログラミングと組み合わせることで、同様の識別機能を確保しながら効率を数十倍高めることができます。何百回も。
#データベースの作成とクエリ
入力観測画像の場合、データベースを通じてマッピング履歴 (画像/点群/特徴点) をクエリして、現在の観測画像の最も可能性の高い観測値を取得します。画像. マップサブセット(画像/点群/特徴点)を取得し、マップと観測情報を照合し、変換行列を計算し、観測カメラの姿勢を取得します。
インデックスは、このプロセスを高速化するための鍵です。データベース自体は巨大になる傾向があります。北京市朝陽市のジョイシティ2階で美団のパウチロボットを試験運用した例では、3台の深度カメラが設置され、審査後も900×600の写真が8万枚近く使用された。測位のリアルタイム性を考慮すると、クエリと 80,000 枚の画像を毎回 1 つずつ比較することは不可能であるため、アルゴリズム全体を高速化するにはインデックス技術を使用する必要があります。この技術は、SLAMにおけるループバックテストや画像検索、ビジョンにおける位置認識などと重なる部分が多いため、以下では一般的な手法のみを紹介します。
画像には複数の特徴点があります。特徴点は、VLAD (ローカルに集約された記述子のベクトル) エンコードなど、最初にエンコードする必要があり、ローカル記述子は、画像のグローバルな説明。次に、kd-tree などのインデックスを使用して、イメージ レベルのクエリを実行します。もちろん、階層型バッグオブワードモデル (Bag-of-words、BoW) の順方向インデックスおよび逆方向インデックス方式など、エンコードとインデックス付けを同時に実行することもできます。
VLAD エンコード
VLAD (ローカルに集約された記述子のベクトル)[10]、図 7 に示すは、ローカルディスクリプタを集約してコードブックを構成し、ディスクリプタとコードワード(Word)との距離を累積的に計算することでグローバル符号化を行うシンプルな方式です。  ディメンション記述子
ディメンション記述子  は、
は、 コードワードのコードブックを通じてエンコードされ、
コードワードのコードブックを通じてエンコードされ、 ディメンションを形成します記述ベクトルの場合、ベクトル内の値は、記述子と
ディメンションを形成します記述ベクトルの場合、ベクトル内の値は、記述子と 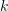 番目の次元の
番目の次元の 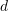 番目のコード ワードとの差です。次に、
番目のコード ワードとの差です。次に、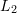 正規化を実行して、最終的な VLAD ベクトルを形成します。
正規化を実行して、最終的な VLAD ベクトルを形成します。
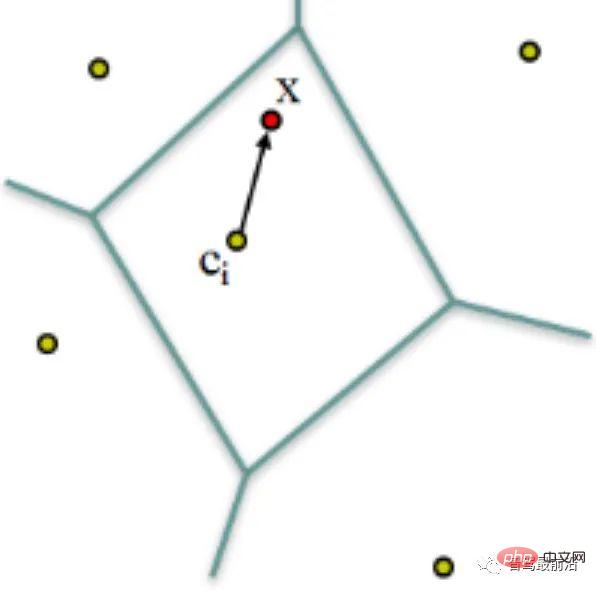
#図 7: VLAD は記述子とコード ワード間の距離によってエンコードされます
ここでは特に DenseVLAD[11] と NetVLAD[12] について紹介します。 Torii らは、DenseSIFT がクエリとマッチングの両方で標準 SIFT よりも優れていることを証明しました。 DenseVLAD は、2 ピクセル間隔のグリッド状のサンプリング パターンで 4 つのスケールで SIFT ポイントを抽出します。 2,500 万個の記述子をグローバルにランダムにサンプリングし、K-means アルゴリズムを使用して 128 個のコードワードのコードブックを生成します。 VLAD ベクトルは、正規化後に PCA (主成分分析) を使用して次元削減され、最終的な 4096 次元の DenseVLAD ベクトルが形成されます。図 8 に示すように、DenseSIFT を使用してマッチングした後の内部点 (緑色) の数が多くなります。

図 8: DenseSIFT と標準 SIFT の特徴点、マッチング後の内部点 (緑色) の比較
NetVLAD は、VLAD エンコードの識別性を高めるために、VLAD に監視情報を追加します。図 9 に示すように、赤と緑の 2 つの記述子が、一致すべきではない 2 つの画像からのものであると仮定します。両方とも VLAD 中心 (×) からより大きな半径と同様の距離にあるため、L2 正規化後、エンコードされた値は非常に類似します。赤と緑の記述子に対応するピクチャが一致しないという監視情報を追加した後、NetVLAD によって生成された中心点 (★) により 2 つの記述子をより適切に区別し、エンコードされた距離 (半径) の差を増やすことができます。
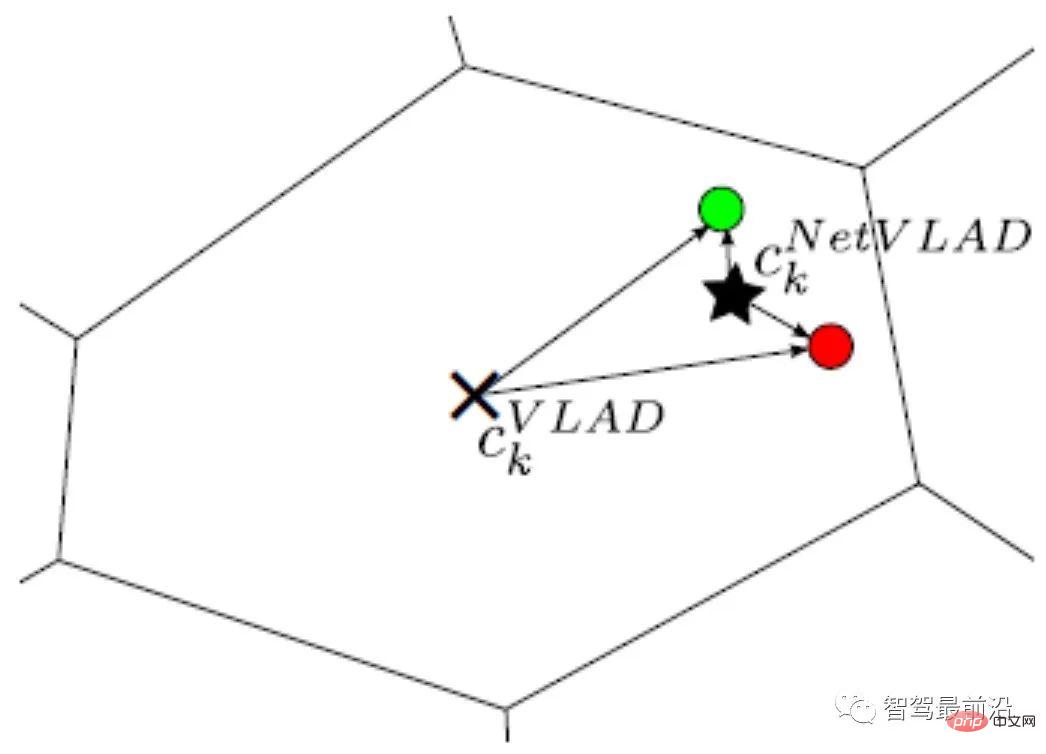
図 9: NetVLAD クラスタリング センター (×) と VLAD クラスタリング センター (★) の比較BoW コーディング インデックスバッグ オブ ワード モデル BoW [13, 14] に基づく機能コーディングとその設計アイデアは、コンピューター ビジョンの開発において決定的な役割を果たしており、今後もそうはならないでしょう。ここで紹介されています。この記事では、2D クエリ画像マッチング 2D 画像データベースを例として、一般的な BoW エンコーディングとインデックス付けの統合モデルを紹介します。図 10 に示すように、辞書 (Vocabulary) は階層的手法を用いて生成され、データセット内のすべての記述子について空間が木構造に従って分割され、各階層は k-means クラスタリングによって計算されます。最後のリーフ ノードはコード ワードに相当します (図 10 には 9 つのコード ワードがあります)。
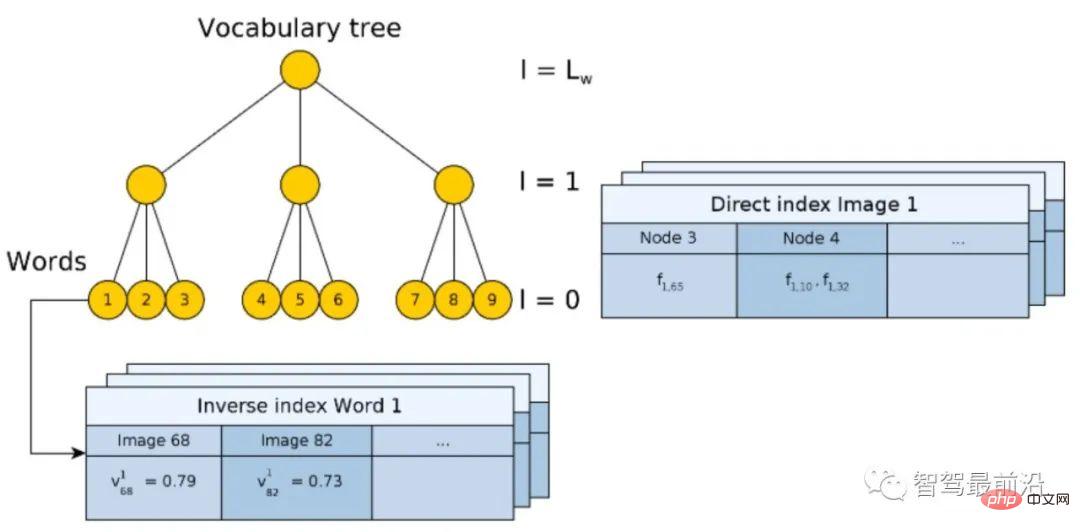
#図 10: 順方向インデックスと逆方向インデックスを備えた階層型 BoW モデル
ツリー構築プロセスは、実際には元の画像をエンコードするプロセスです。ただし、エンコード自体は検索プロセスを高速化するものではなく、VLAD と同様に、データベース内の画像と 1 つずつ比較する必要があります。したがって、ここでは、符号化されたベクトルを比較する必要のない逆インデックス (Inverse Index) が設計されています。原理を図 11 に示します。クエリ画像 (Query image) の場合、抽出された記述子は BoW に入力され、最終的にコードワード リーフ ノード (ビジュアル ワード) k に分類されます。各コードワードはインデックスに対応し、コードワード 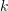 の重みをデータベース
の重みをデータベース  番目の画像に記録します
番目の画像に記録します 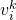 (図10)。ここで、重みは TF-IDF (用語頻度 – 逆文書頻度) を使用して計算されます。つまり、単語
(図10)。ここで、重みは TF-IDF (用語頻度 – 逆文書頻度) を使用して計算されます。つまり、単語 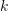 がある画像
がある画像  に頻繁に出現し、他の画像では出現頻度が低い場合、この単語の画像識別性と重み値が優れていることになります。
に頻繁に出現し、他の画像では出現頻度が低い場合、この単語の画像識別性と重み値が優れていることになります。 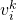 さらに高くなります。最後に、投票メカニズムを通じて一致する画像が選択されます。逆インデックスは必ずしもツリー構造の BoW 上に構築されるわけではなく、高速なクエリの方法を提供するだけであることにも注意してください。
さらに高くなります。最後に、投票メカニズムを通じて一致する画像が選択されます。逆インデックスは必ずしもツリー構造の BoW 上に構築されるわけではなく、高速なクエリの方法を提供するだけであることにも注意してください。
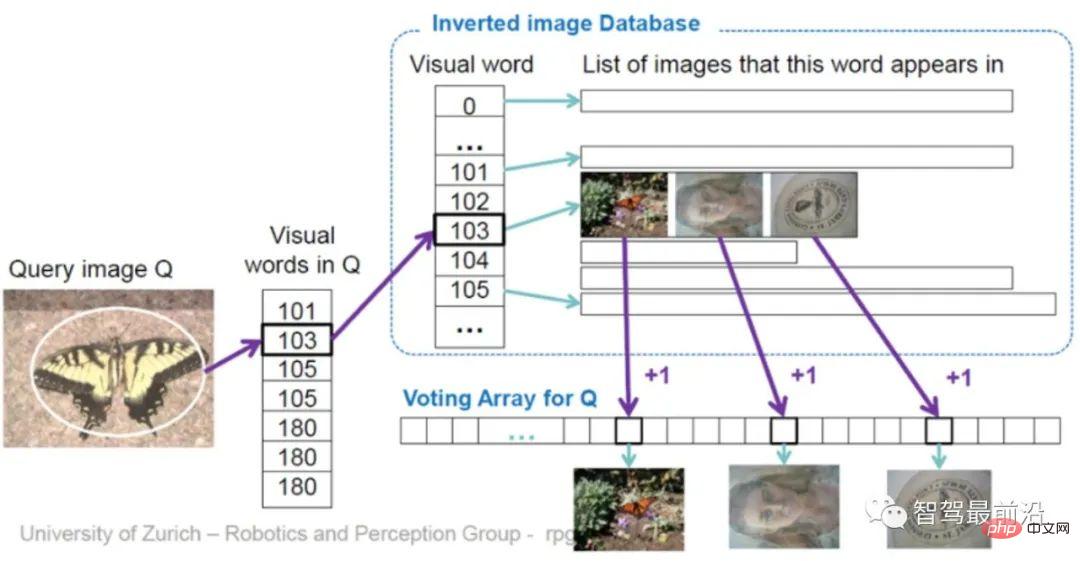
#図 11: 逆インデックス投票メカニズムを介して画像を直接クエリする
フォワード インデックス (ダイレクト インデックス) の主な機能は、BoW を構築するときにデータベース画像の特徴点がどのノードに該当するかを記録することです。このようにして、画像がクエリされるときに、インデックスを介して直接特徴点を抽出することができます。
3D 点群クエリ
2D 画像クエリでは、まず画像がセマンティック レベルからクエリされるため、画像は特徴点の空間範囲を制限します。 3D 点群クエリにはそのような制約がないため、多くの困難があります。空間的な連続性を考慮する必要がある場合は、クエリされたすべての点が観測可能な範囲内にあるかどうかなどを考慮します。ここでは、TPAMI 2016 で Sattler によって公開されたメソッド [15] のみを紹介します。何年にもわたる改良を経て、このメソッドのフレームワークは比較的シンプルで完全なものになりました。辞書エンコード検索の手順は前のセクションの内容と重複するため、ここではアクティブ検索と可視性フィルタリングの 2 つのメカニズムのみを紹介します。
アクティブ検索は主に、一致する 3D ポイントを空間内で可能な限り近づけ、幾何学的意味を持たせることを目的としています。図 12 に示すように、赤い点は、一連のエンコードと洗練のプロセスを通じて点群内の点と一致します (赤い線)。提案された優先順位付けフレームワークによれば、最も高い確率で 3D 点が点群から検出され、逆に (青い線) クエリ画像内の対応する 2D 点と一致します。

図 12: アクティブな検索
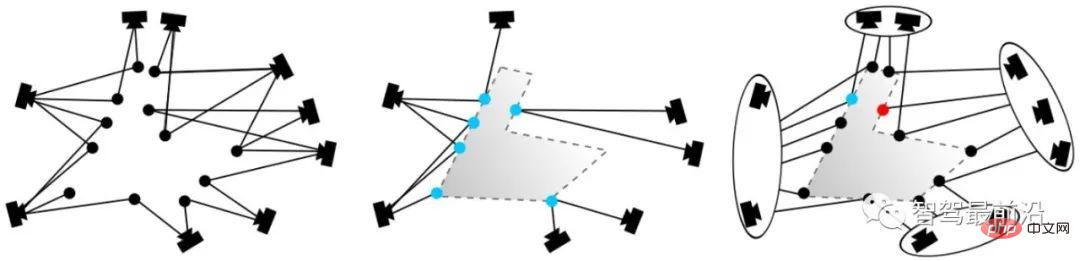
##図 13: 可視性フィルタリング 可視性フィルタリング
主な目的は、一致したポイントをカメラにできるだけ見えるようにすることです (位置決めは監視されていないため、一致したポイントが正しいかどうかを知ることはできません)。ここで採用されている方法は、SfM を使用して 3D 点群マップを作成する際に、2 部の視程グラフを作成することです。図 13 (左) に示すように、ある点を 2 台のカメラで同時に観察できる場合、位相関係が確立されます。図 13 (中) では、青い点が対応点であり、観察の観点からは矛盾しています。既存のトポロジに対してグラフ クラスタリングを実行すると、図 13 (右) に示すように、カメラが 2 つのグループにグループ化されます。このようにして、新しいグラフ トポロジ関係を生成できます。次に、各サブグラフ間の重なりを判断することにより、見えない可能性が高い点を除外します。双眼カメラと RGB-D カメラは深度を取得できますが、2D 画像をクエリすると限られた範囲内の 3D 特徴点座標も取得できることに注意してください。ただし、現在の技術的な制限により、 、複雑な屋内マテリアルや大規模な屋外シーンでは、深度は信頼できません。したがって、2D 画像点と 3D 点群マップのマッチングは依然として重要な方法です。
特徴点マッチング
古典的な RANSAC
ランダム サンプル コンセンサス アルゴリズム (ランダム サンプル コンセンサス、RANSAC) [16] は古典的なデータです。フィルタリングおよびパラメータフィッティングアルゴリズム。データの分布(インライア)が特定の数学モデルに準拠していると仮定し、反復計算により外れ値やノイズ点を除去し、同時に確率的に最適なモデルパラメータを取得します。グローバル ポジショニングでは、内部点は正しい一致を指し、外部点は不正確な一致を指し、パラメトリック モデルは一致する点のペアの空間変換行列を指します。図 14 に示すように、RANSAC アルゴリズムによる最適化の後、マッチングはより合理的になります。 RANSAC が見つけることを期待する一致するサブセットは、内部点の再投影誤差ができるだけ小さいこと、内部点の数ができるだけ大きいという 2 つの指標を満たす必要があります。したがって、基本的なプロセスは次のとおりです。#① 初期サブセットをサンプリングします。
② 変換行列を計算します。
③ 変換行列に基づいてマッチング点の再投影誤差を計算します。
④ 大きな誤差のある点を削除します
⑤ ①~④をループして、指標に最もよく適合する一致ソリューションを保持します。

図 14: (上) 元の特徴のマッチング、(下) RANSAC アルゴリズムによって最適化されたマッチング
このうち、最初の候補マッチングは記述子間の距離に基づいて生成されますが、再投影誤差はキーポイントの空間位置にのみ関係し、記述子自体とは関係ありません。具体的な射影行列の手法については「2.4 姿勢計算」を参照してください。 RANSAC アルゴリズムは、元のマッチング誤差とパラメータ選択の影響を受けるため、アルゴリズムが合理的であるのに十分な確率を保証できるだけであり、必ずしも最適な結果が得られるわけではないことに注意してください。アルゴリズム パラメーターには主にしきい値と反復回数が含まれます。 RANSAC が信頼できるモデルを取得する確率は反復回数に正比例し、取得された一致の数はしきい値に反比例します。したがって、実際の使用では、より良い結果を得るために、異なるパラメータ設定を繰り返し試す必要がある場合があります。
学者らは、古典的な RANSAC アルゴリズムに多くの改良を加え、図 15 に示すように、グローバル RANSAC (Universal-RANSAC) の構造図 [17] を提案し、普遍的な RANSAC アルゴリズムを形成しています。 RANSAC アルゴリズム: 適応型 RANSAC アーキテクチャは、事前フィルタリング、最小サブセット サンプリング、最小サブセットからの信頼性の高いモデル生成、パラメータ検証、モデル改良など、RANSAC のほぼすべての改善点をカバーしています。
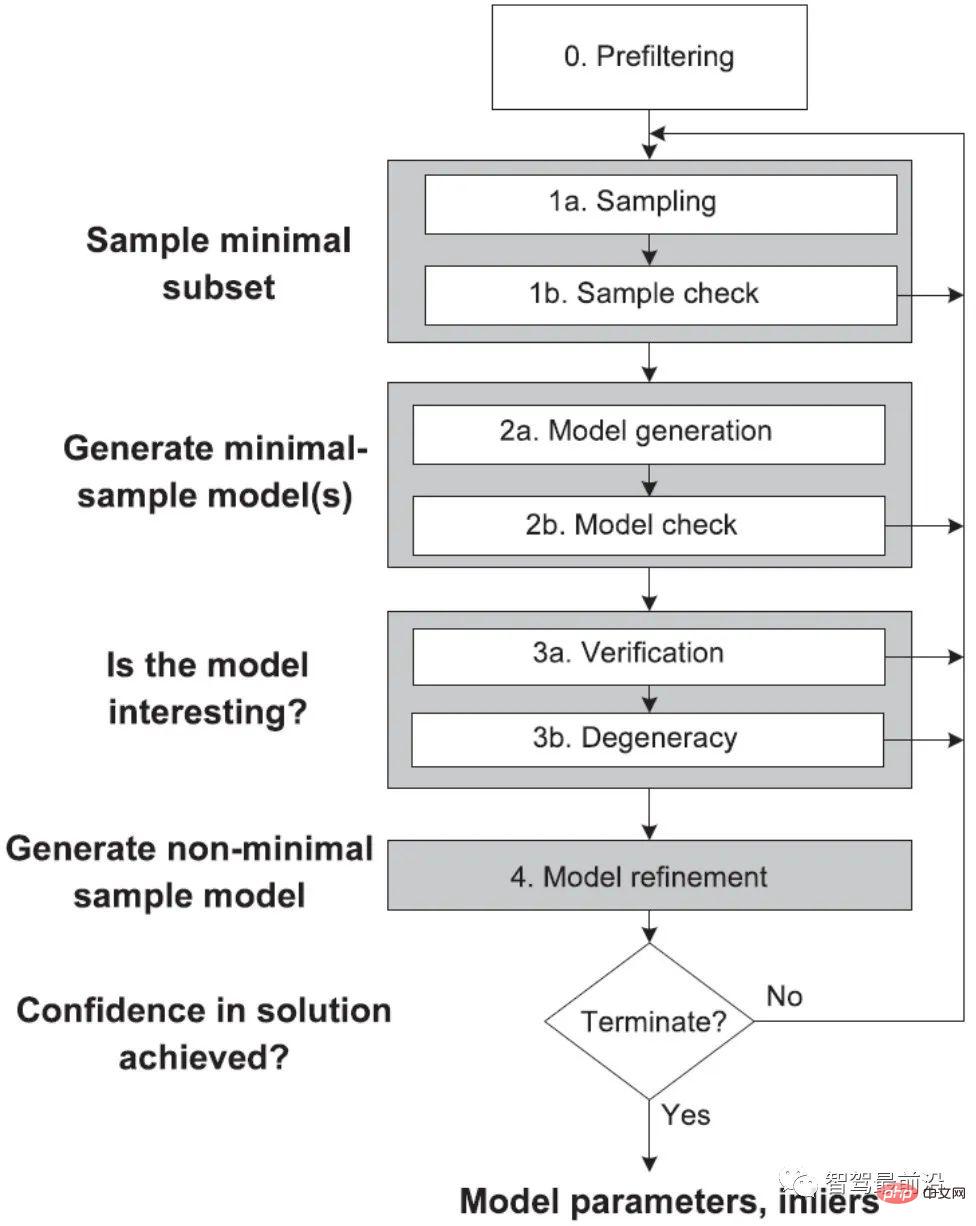
##図 15: Universal-RANSAC ユニバーサル アルゴリズム フレームワーク
DifferentiableRANSAC
手動記述子は依然として測位分野で高いパフォーマンスを示しているため、一部の学者は、アルゴリズム フレームワークの特定の部分を置き換えるために深層学習の使用を検討し始めています。エンドツーエンドの姿勢推定モデルを直接使用して、従来の方法を完全に置き換えます。微分可能 RANSAC (DSAC) [18] は、決定論的な仮説選択を確率論的な仮説選択に置き換えて、RANSAC プロセスを導き出すことを目的としています。指標の違いは、誤差が特徴点ではなく画像全体に基づいており、特徴点一致をスクリーニングする元のプロセスが、カメラ姿勢仮説 h を確率で直接スクリーニングするプロセスに置き換えられることです。現在の方法には比較的大きな制限がありますが、DSAC は、現在の教師なし測位アルゴリズム フレームワークに事前知識を追加する方法についての実現可能なアイデアを提供します。

ビット ポーズ計算
であり、変換モーメントの同次形式  は次のとおりです。
は次のとおりです。 
 このうち、
このうち、
は回転行列、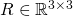 は平行移動行列です。
は平行移動行列です。 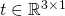
2.4.1 2D-2D 変換行列の計算
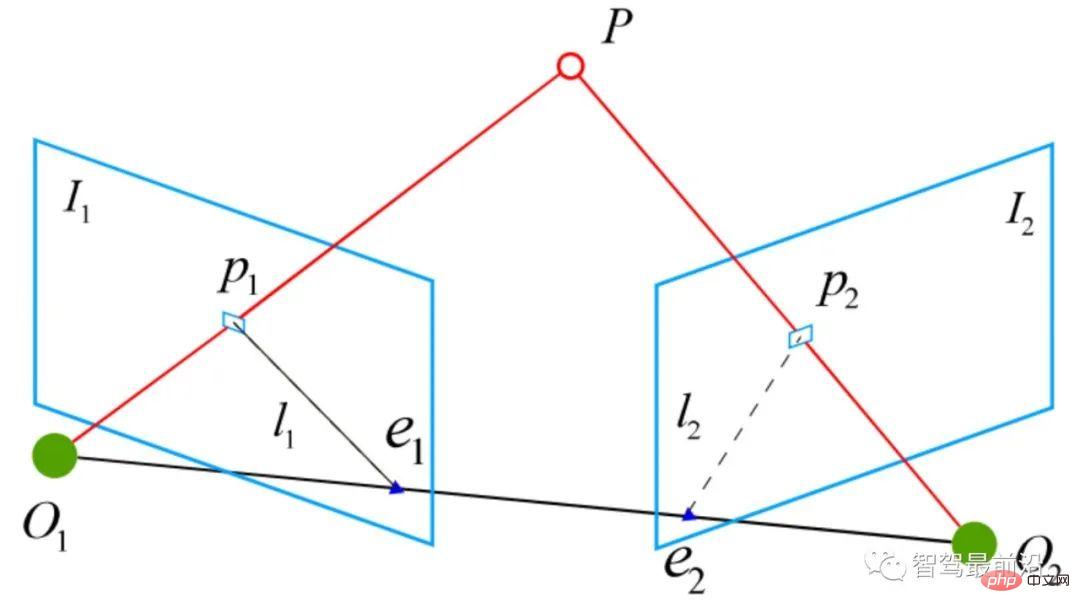
図 17: 2D-2D 変換行列の計算エピポーラ幾何学
2 つの 2 次元画像内の一致する特徴点のペア (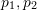 ) は、正規化された平面上にあります。座標は (
) は、正規化された平面上にあります。座標は ( 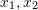 )、対応する変換行列はエピポーラ制約を通じて計算する必要があります。図 17 に示すように、その幾何学的意味は、
)、対応する変換行列はエピポーラ制約を通じて計算する必要があります。図 17 に示すように、その幾何学的意味は、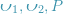 が 3 つの同一平面上にあることです。この面は極面とも呼ばれ、
が 3 つの同一平面上にあることです。この面は極面とも呼ばれ、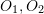 はベースラインと呼ばれ、
はベースラインと呼ばれ、 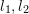 は極線と呼ばれます。エピポーラ制約には平行移動と回転の両方が含まれており、次のように定義されます。
は極線と呼ばれます。エピポーラ制約には平行移動と回転の両方が含まれており、次のように定義されます。

そのうち、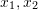 は ## です。
は ## です。 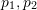 # 正規化平面上の座標。∧ は外積演算子です。式の中間部分を基本行列
# 正規化平面上の座標。∧ は外積演算子です。式の中間部分を基本行列 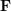 と必須行列
と必須行列 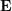 として計算すると、次のようになります。 ##
として計算すると、次のようになります。 ##
必須行列 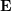 にはスケール情報がないため、E にゼロ以外の定数を乗算した後でもエピポーラ制約は保持されます。
にはスケール情報がないため、E にゼロ以外の定数を乗算した後でもエピポーラ制約は保持されます。 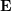 は古典的な 8 点法 (8 点アルゴリズム) で解くことができ、その後分解して
は古典的な 8 点法 (8 点アルゴリズム) で解くことができ、その後分解して 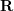 、
、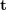 ## を取得します。 #。したがって、2D-2D 変換行列解法には 2 つの欠点があることがわかります。1 つは、単眼視覚にはスケールの不確実性があり、スケール情報は初期化中に
## を取得します。 #。したがって、2D-2D 変換行列解法には 2 つの欠点があることがわかります。1 つは、単眼視覚にはスケールの不確実性があり、スケール情報は初期化中に 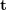 によって提供される必要があります。同様に、単眼の初期化は純粋な回転だけではなく、十分な程度の平行移動が必要です。そうでない場合、
によって提供される必要があります。同様に、単眼の初期化は純粋な回転だけではなく、十分な程度の平行移動が必要です。そうでない場合、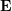 はゼロになります。
はゼロになります。
#2.4.2 2D-3D 変換行列の計算
2D-3D マッチングは姿勢推定において重要です。 。一般に、PnP メソッドが使用されます。つまり、 は、2D-3D 対応点の変換行列を解き、カメラのポーズを取得することが知られています。 3D 点 P(X, Y, Z) をカメラの撮像面 ( ) に投影します。
) に投影します。 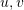

はスケール  です。この方程式の解は線形方程式問題に還元でき、各特徴は次の 2 つの線形制約を提供できます。
です。この方程式の解は線形方程式問題に還元でき、各特徴は次の 2 つの線形制約を提供できます。 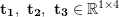

3D-3D変換行列計算
3D ポイント間の変換行列は、反復最近点 (ICP) アルゴリズムを使用して解決できます。点ペア マッチング ( ) の結果が正しいと仮定すると、得られた変換行列は再投影誤差
) の結果が正しいと仮定すると、得られた変換行列は再投影誤差  を最小限に抑える必要があります。 SVD を使用して最小二乗問題を解決することもできます:
を最小限に抑える必要があります。 SVD を使用して最小二乗問題を解決することもできます:
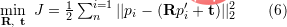
またはリー代数に基づく非線形最適化手法バンドル調整を使用して # を解決します。
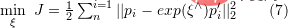
##このうち、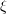 はカメラのポーズを表します。ここでの最適化目標は、2D-3D マッチングにおけるバンドル調整の目標と似ていますが、元の画像は双眼カメラまたは RGB によって処理されているため、カメラの内部パラメータ
はカメラのポーズを表します。ここでの最適化目標は、2D-3D マッチングにおけるバンドル調整の目標と似ていますが、元の画像は双眼カメラまたは RGB によって処理されているため、カメラの内部パラメータ 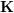 を考慮する必要はありません。 -D 深度カメラ: 2D 点がカメラの撮像面から 3D 世界に投影されます。
を考慮する必要はありません。 -D 深度カメラ: 2D 点がカメラの撮像面から 3D 世界に投影されます。
ICP 問題には、独自の解決策と無限の解決策があることが証明されています。したがって、一意な解が存在する場合、最適化関数は凸関数に相当し、その最小値が大域最適解となり、どのような初期化を行ってもこの一意な解が得られる。これは ICP 法の大きな利点の 1 つです。
#この記事では、画像の説明、マッピング クエリ、特徴マッチング、姿勢計算の 4 つの側面から特徴点に基づく姿勢推定アルゴリズムを紹介します。従来の視覚的全地球測位手法が依然として実用化の第一選択ですが、従来の手法は、特徴点が正しく定義され、正しく抽出され、正しく照合され、正しく観察されるという前提に基づいており、この前提は視覚にとって非常に重要です。それ自体、大きな挑戦です。第二に、従来の手法はエンドツーエンドではなく多段階のフレームワークであるため、各リンクとリンク間の相互作用には多くのパラメータ調整が必要であり、各リンクのテクノロジーを個別の研究方向として使用できます。実際のアプリケーションでは、特定のシナリオに対応する多くのトリックを追加する必要があり、エンジニアリングがより複雑になります。そして、エンドツーエンド方式に対する人々の期待により、PoseNet、VLocNet、HourglassNet などのネットワークが誕生し、ベンチマークで良好な結果を達成しています。著者は、現在のエンドツーエンド手法にはまだ多くの問題があると考えていますが、主な問題としては、損失関数に幾何学的制約が欠けていること、マップを構築する際の姿勢の 6 自由度空間が連続的ではないこと、入力空間との適切なマッピングを形成することが困難であり、対応する位置、姿勢回帰、改良メカニズムなどが欠如しています。ディープラーニングは非線形空間の最も強力なモデリングツールとして、今後測位の分野でさらに登場する可能性は否定できません。
視覚的な位置決めそのものに戻ると、視覚の最も重要な利点は、低コスト、豊富なセマンティクス、および使用シナリオの制限がほとんどないことです。したがって、視覚に焦点を当て、他の低コストセンサーによって補完される位置決め融合ソリューションも、将来的には重要なテーマとなるでしょう。
以上がWanzi解析による自動運転特徴点に基づく全地球測位技術の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。