ディープラーニングでマスターしなければならない13の確率分布

1. 確率分布の概要

• 共役とは、共役分布の関係があることを意味します。
• ベイズ確率理論では、事後分布 p(θx) と事前確率分布 p(θ) が同じ確率分布族に属する場合、事前分布と事後分布は共役分布と呼ばれ、事前分布は共役分布と呼ばれます。尤度関数の事前共役。 Conjugate prerior ウィキペディアはこちら (https://en.wikipedia.org/wiki/Conjugate_prior) です。
• 複数の分類は、ランダム分散が 2 より大きいことを意味します。
• n 回ということは、事前確率 p(x) も考慮することを意味します。
• 確率についてさらに詳しく知りたい場合は、[パターン認識と機械学習、Bishop 2006] を読むことをお勧めします。

2. 分布確率と特性

1. 一様分布 (連続)

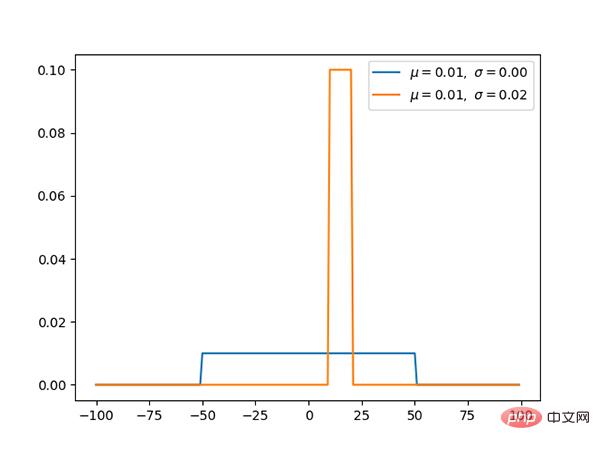
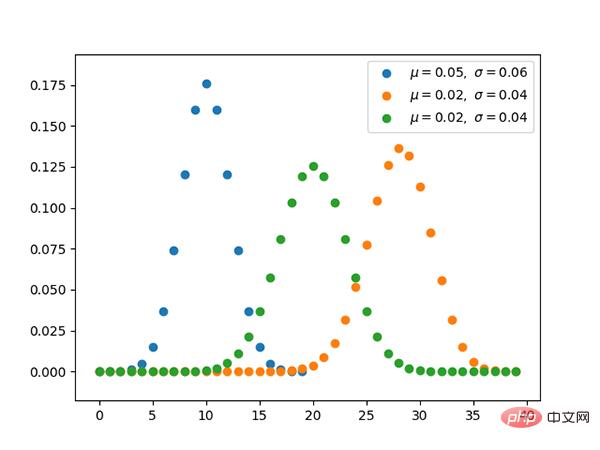
コード: https://github.com/graykode/distribution-is- all-you-need/blob/master/uniform.py

一様分布は [a, b] で同じ確率値を持ち、単純な確率分布です。

2. ベルヌーイ分布 (離散)

コード: https://github.com/graykode/distribution-is-all-you-need/ blob/master/bernoulli.py

• 事前確率 p(x) はベルヌーイ分布を考慮しません。したがって、尤度を最大化するように最適化すると、簡単に過剰適合になる可能性があります。
• バイナリクロスエントロピーを使用して二項分類を分類します。その形式はベルヌーイ分布の負の対数と同じです。画像

3. 二項分布 (離散)

コード: https://github.com/graykode/distribution-is-all-you-need/blob/master/ binomial .py

• パラメータ n と p を持つ二項分布は、一連の n 回の独立した実験における成功数の離散確率分布です。
• 二項分布は、事前に取り出す数量を指定して事前確率を考慮した分布です。

4. マルチベルヌーイ分布、カテゴリ分布 (離散)

コード: https://github.com/graykode/distribution - is-all-you-need/blob/master/categorical.py

• 多重ベルヌーイ分布はカテゴリ分布と呼ばれます。
• クロスエントロピーは、負の対数をとるマルチベルヌーイ分布と同じ形式をとります。

5. 多項式分布 (離散)

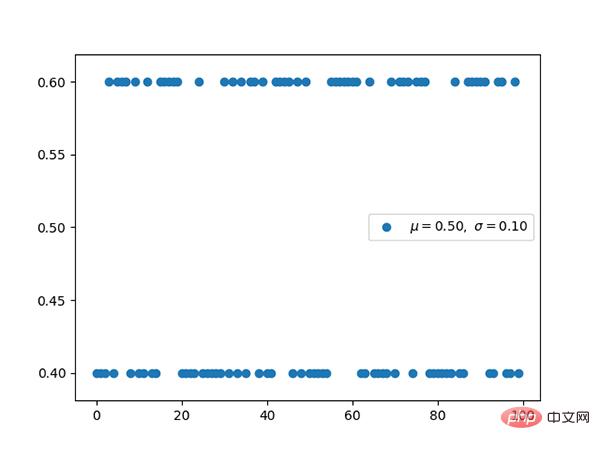
コード: https://github.com/graykode/distribution-is-all-you -need/blob/master/multinomial.py

多項分布とカテゴリ分布の関係は、ベルヌール分布と二項分布の関係と同じです。

6.β ディストリビューション (継続)

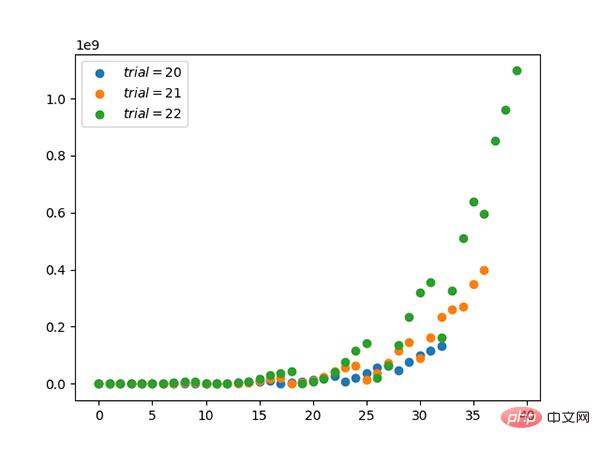
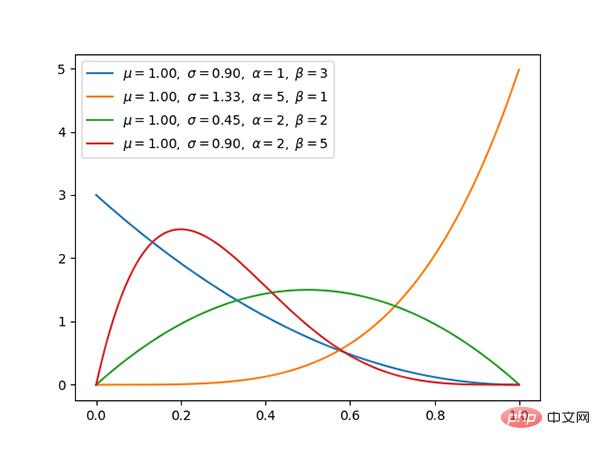
コード: https://github.com/graykode/distribution-is-all-you-need/ blob/master/beta.py

• ベータ分布は、二項分布およびベルヌーイ分布と共役です。
• 共役を使用すると、既知の事前分布を使用して事後分布をより簡単に取得できます。
• β分布が特殊な場合(α=1、β=1)を満たす場合、一様分布は同じになります。

7.ディリクレ分布 (連続)

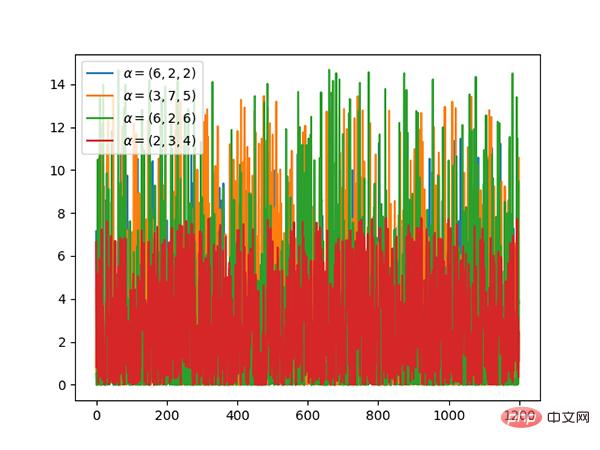
コード: https://github.com/graykode/distribution-is-all-you -need/blob/master/dirichlet.py

• ディリクレ分布と多項式分布は共役です。
• k=2 の場合、ベータ分布になります。

8. ガンマ分布 (連続)

コード: https://github.com/graykode/distribution-is-all-you -need/blob/master/gamma.py

• gamma(a,1)/gamma(a,1) gamma(b,1) が beta(a,b) と同じ場合、ガンマ分布はベータ分布になります。
• 指数分布とカイ二乗分布はガンマ分布の特殊なケースです。

9. 指数分布 (連続)

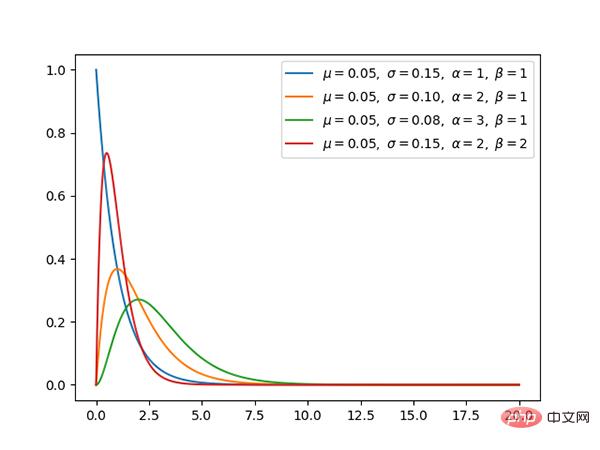
コード: https://github.com/graykode/distribution-is-all-you -need/blob/master/exponential.py

指数分布は、α が 1 の場合の γ 分布の特殊なケースです。

10. ガウス分布 (連続)

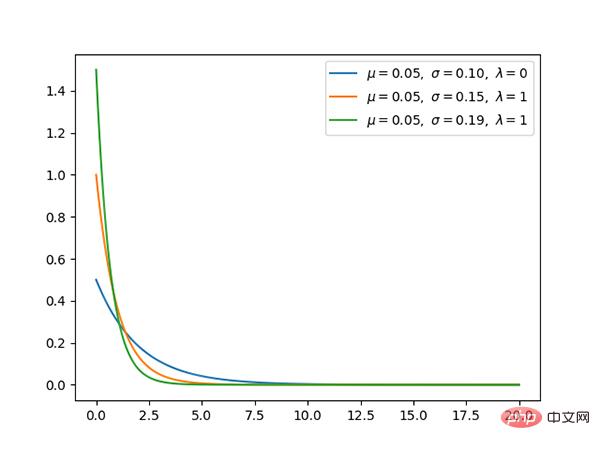
コード: https://github.com/graykode/distribution-is-all-you-need/ blob/master/gaussian.py

ガウス分布は、非常に一般的な連続確率分布です。

11. 正規分布 (連続)

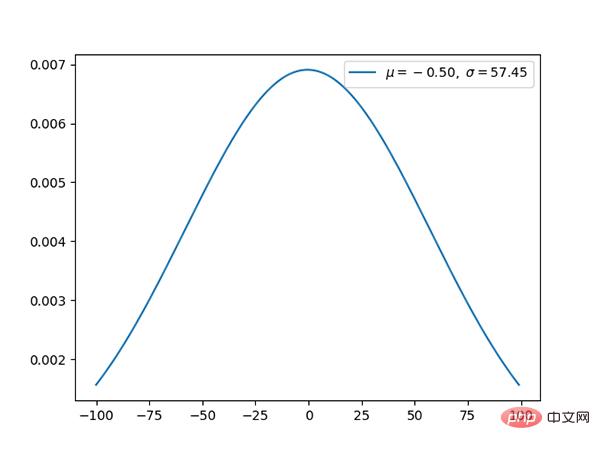
コード: https://github.com/graykode/distribution-is-all-you-need / blob/master/normal.py

正規分布は、平均が 0、標準偏差が 1 の標準ガウス分布です。

12. カイ二乗分布 (連続)

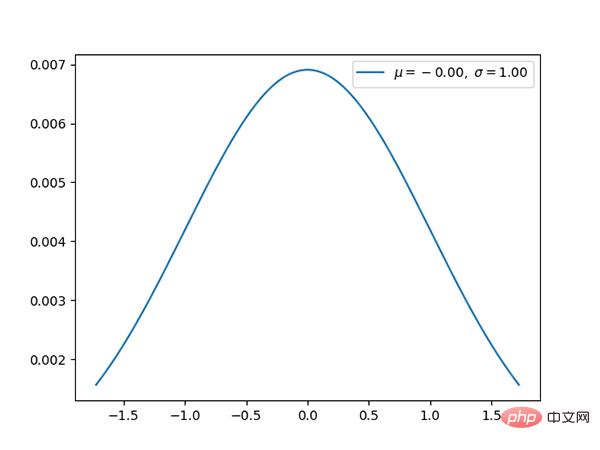
コード: https://github.com/graykode/distribution-is-all-you- need /blob/master/chi-squared.py

• k 自由度のカイ二乗分布は、k 個の独立した標準正規確率変数の二乗和の分布です。
• カイ二乗分布はベータ分布の特殊なケースです

13.t 分布 (連続)

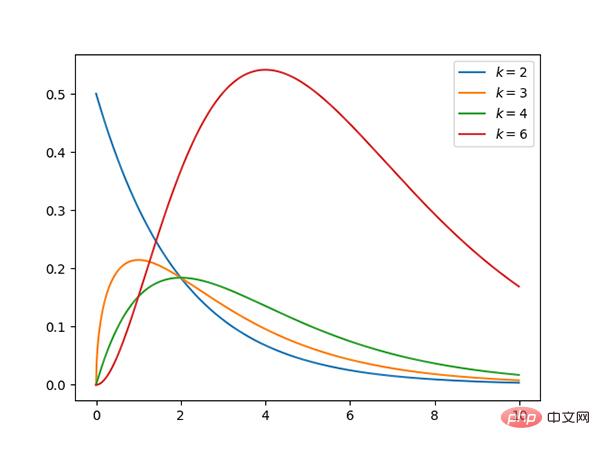
コード: https://github.com/graykode/distribution-is-all-you-need/blob/master/student-t.py

t 分布は、正規分布に似た対称の釣鐘型分布です。これは、平均を大きく下回る値を生成する可能性が高いことを意味します。

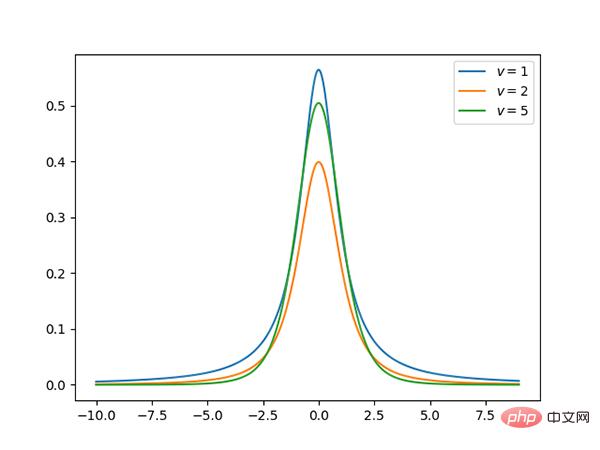
経由：https://github.com/graykode/distribution-is-all-you-needa

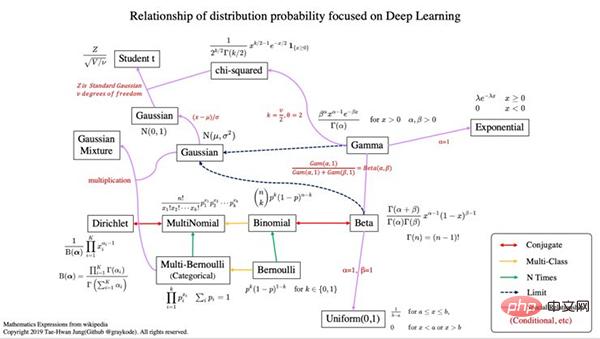
以上がディープラーニングでマスターしなければならない13の確率分布の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。