Pythonを使ってミサイルの自動追尾を実装、超燃える！

皆さんこんにちは、私はブラザーJです。

何らかの数学的基礎がなければ、これを計算することは困難です。しかし、コンピュータの場合は異なり、コンピュータの非常に速い計算速度を利用して、微分の考え方を使用し、三角法の簡単な知識を追加することでそれを実現できます。

さて、早速、そのアルゴリズムの原理と図を見てみましょう:

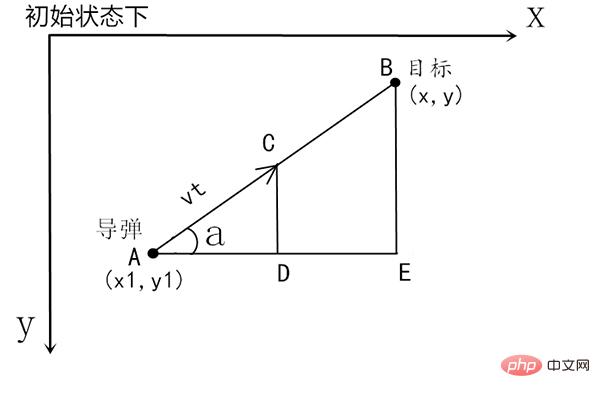
後で pygame を使用してデモンストレーションするため、 y 軸が下を向いた座標系なので、ここでも y 軸が下を向いた座標系を使用します。

アルゴリズムの一般的な考え方は、上の図に基づいて、時間 t を十分に小さいセグメント (1/1000 など、タイム スライスが小さいほど正確になります) に分割することです。セグメントは上記のように三角形を構築してミサイルを計算し、次のタイムスライスでの歩行方向 (つまり ∠a) と移動距離 (つまり vt=|AC|) このときターゲットは 2 回目にも移動しますこのとき、計算された点 C が 2 番目のタイム スライスの開始点となり、点 C と 2 番目のタイム スライス上の新しいターゲット ポイントに三角形を構築して新しい vt を計算し、3 番目のタイム スライスに入力します。スライスして繰り返します。

ミサイルとターゲットの初期座標がそれぞれ (x1, y1)、(x, y) であると仮定し、直角三角形 ABE を作成します。この三角形はサイン値とコサイン値を見つけるために使用されます。 ∠a の vt は自分で設定します 点 A の x 座標と y 座標がそれぞれどれだけ移動したかを計算する必要があります 移動量は AD と CD の長さです この 2 つは掛け算できますそれぞれ vt cos(a) と sin(a) によって計算されます。

sin(a) と cos(a)、サインと傾き、コサイン隣接と傾きを計算します。斜辺は 2 点距離の公式を使用して計算できます。

#So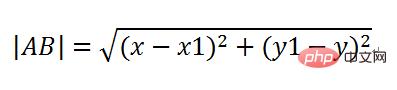

AC の長さは、ミサイルの速度に時間を乗じたもので、|AC|=vt となり、その後、 AD と CD は計算できるため、タイム スライスが経過すると、ミサイルは新しい位置点 C に出現するはずで、その座標は古い点 A の x プラス AD と y マイナス CD になります。

したがって、点 C の新しい座標は次のとおりです:

この操作を繰り返し繰り返してください。最初のタイム スライスと 2 番目のタイム スライスを一緒に見てみましょう: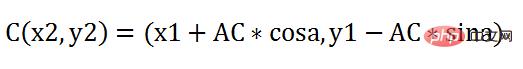

最初のタイム スライスは、ABE というタイム スライスによって構築された三角形です。ターゲット B 点から D 点まで、ミサイルは C 点にあるので、新しい三角形 CDF を構築し、先ほどの計算プロセスを繰り返します。図の角度 ∠b がミサイルが回転する必要がある角度です。現実には、毎回かかるだけです フィルムでミサイルの方向を修正するだけです ミサイルの方向を変える方法は、私たちが研究する必要がある問題ではありません。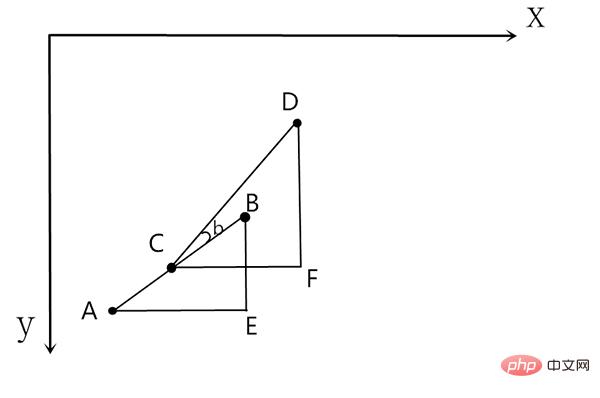

わかりました、私は使っているので、最近、Python の pygame ライブラリを使って小さなゲームを作成しましたが、次に pygame を使用してこの効果を示します。効果は次のとおりです:

非常に簡単なコードは次のとおりです:

import pygame,sys
from math import *
pygame.init()
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/red_pointer.png').convert_alpha()
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
old_angle=0
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点线段的弧度值
x1,y1=(x1+section*cosa,y1-section*sina)
d_angle = degrees(angle)#弧度转角度
screen.blit(missile, (x1-missile.get_width(), y1-missile.get_height()/2))
dis_angle=d_angle-old_angle#dis_angle就是到下一个位置需要改变的角度
old_angle=d_angle#更新初始角度
pygame.display.update()

ミサイルを粒子としてのみ考える場合は、上記のアルゴリズムで十分ですが、粒子は頭尾であっても回転する必要がないため、ミサイルの回転は行いませんでした。もちろん、この前提は、読み込むミサイル画像が非常に小さい場合、回転しなくても問題ないように見えるということです。しかし、pygame で回転を行うのは簡単な作業ではありません。まず画像を長方形に置き換えてから、回転関数を追加して効果を確認しましょう

missiled = pygame.transform.rotate(missile, -(d_angle))
screen.blit(missiled, (x1-missile.get_width(), y1-
missile.get_height()/2))

画像のせいで座標点は左上隅の点であるため、画像の座標を矢印の先端に固定したい場合は、画像の長さを短くして画像の実際の印刷位置 x を小さくするだけで済みます。 y 幅を半分に縮小します。しかし、実際のランニング効果は良好ではありません:

大致方向相同，但是图片箭头的尖点并没有一直跟随鼠标，这是为什么呢。经过一番研究，我发现原来是这个图旋转的机制问题，我们看看旋转后的图片变成什么样了：

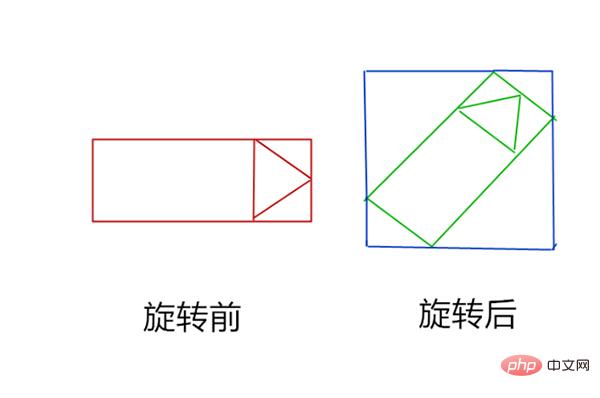
旋转后的图片变成了蓝色的那个范围，根据旋转角度的不同，所变成的图片大小也不一样，我们看旋转90的情况

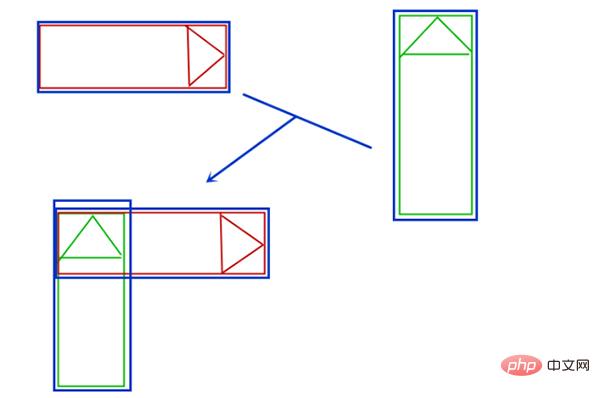
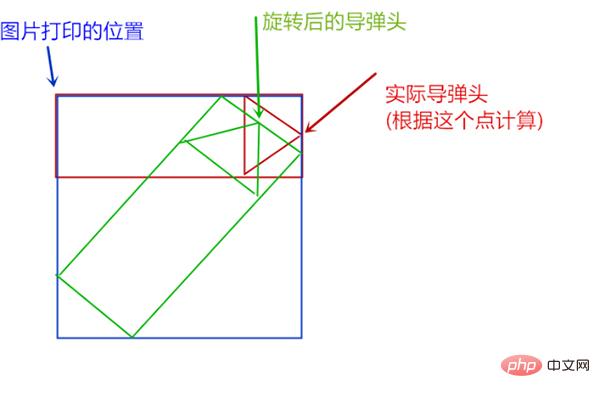
我们发现，旋转后的图片不仅面积变大了，导弹头的位置也变了。那应该怎么解决这个问题呢？思路是，每一次旋转图片以后，求出旋转图的头位置（图中的绿色箭头点），然后把绿图的打印位置移动一下，下，x，y分别移动两个头的距离，就可以让旋转后的导弹头对准实际我们参与运算的那个导弹头的位置，移动后应该是这样的：

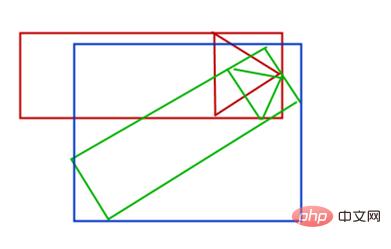
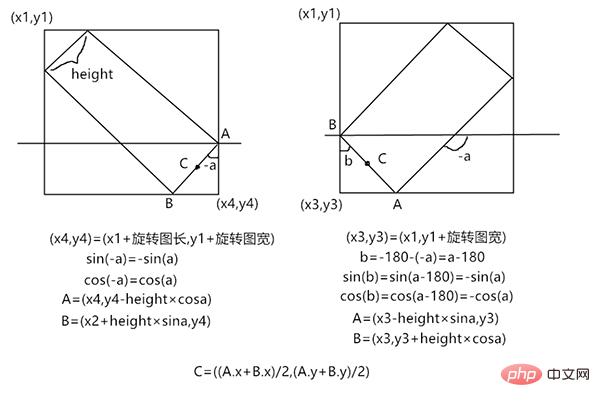
这样，两个导弹头的点就一致了。接下来我们分析求旋转后的导弹头的算法。根据旋转角度的不同，旋转角在不同象限参数不一样，所以我们分为这四种情况

1，2象限

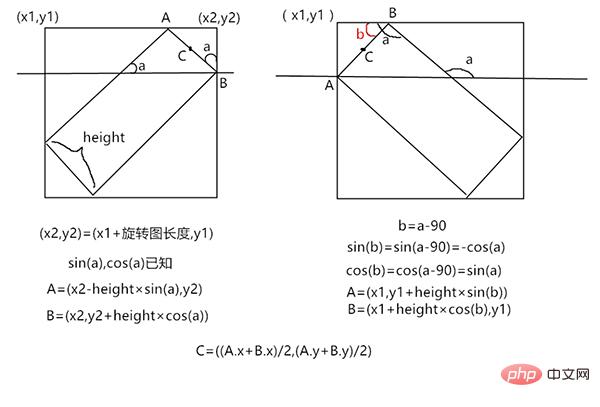
3，4象限，它的旋转只有正负0—180，所以3，4象限就是负角

显示图片的时候我们将他移动

screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))

这里的 (x1-width, y1-height/2) 其实才是上图中的 (x1, y1)

所以最后我们加入相关算法代码，效果就比较完美了

大功告成，最后附上全部的算法代码

import pygame,sys
from math import *
pygame.init()
font1=pygame.font.SysFont('microsoftyaheimicrosoftyaheiui',23)
textc=font1.render('*',True,(250,0,0))
screen=pygame.display.set_mode((800,700),0,32)
missile=pygame.image.load('element/rect1.png').convert_alpha()
height=missile.get_height()
width=missile.get_width()
pygame.mouse.set_visible(0)
x1,y1=100,600 #导弹的初始发射位置
velocity=800#导弹速度
time=1/1000 #每个时间片的长度
clock=pygame.time.Clock()
A=()
B=()
C=()
while True:
for event in pygame.event.get():
if event.type==pygame.QUIT:
sys.exit()
clock.tick(300)
x,y=pygame.mouse.get_pos()#获取鼠标位置，鼠标就是需要打击的目标
distance=sqrt(pow(x1-x,2)+pow(y1-y,2))#两点距离公式
section=velocity*time #每个时间片需要移动的距离
sina=(y1-y)/distance
cosa=(x-x1)/distance
angle=atan2(y-y1,x-x1)#两点间线段的弧度值
fangle=degrees(angle) #弧度转角度
x1,y1=(x1+section*cosa,y1-section*sina)
missiled=pygame.transform.rotate(missile,-(fangle))
if 0<=-fangle<=90:
A=(width*cosa+x1-width,y1-height/2)
B=(A[0]+height*sina,A[1]+height*cosa)
if 90<-fangle<=180:
A = (x1 - width, y1 - height/2+height*(-cosa))
B = (x1 - width+height*sina, y1 - height/2)
if -90<=-fangle<0:
A = (x1 - width+missiled.get_width(), y1 - height/2+missiled.get_height()-height*cosa)
B = (A[0]+height*sina, y1 - height/2+missiled.get_height())
if -180<-fangle<-90:
A = (x1-width-height*sina, y1 - height/2+missiled.get_height())
B = (x1 - width,A[1]+height*cosa )
C = ((A[0] + B[0]) / 2, (A[1] + B[1]) / 2)
screen.fill((0,0,0))
screen.blit(missiled, (x1-width+(x1-C[0]),y1-height/2+(y1-C[1])))
screen.blit(textc, (x,y)) #鼠标用一个红色*代替
pygame.display.update()

以上便是用Python模拟导弹自动追踪的代码实例。

以上がPythonを使ってミサイルの自動追尾を実装、超燃える！の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。