主な技術思想と因果推論手法の概要

はじめに: 因果推論はデータ サイエンスの重要な分野であり、インターネットや業界における製品の反復、アルゴリズム、インセンティブ戦略の評価において重要な役割を果たしています。その役割は、データ、実験、または統計計量経済モデルを組み合わせて、意思決定の基礎となる新しい変化の利点を計算することです。しかし、因果関係の推論は単純なものではありません。まず、日常生活において、人々は相関関係と因果関係を混同することがよくあります。相関関係は、多くの場合、2 つの変数が同時に増加または減少する傾向があることを意味しますが、因果関係は、変数を変更したときに何が起こるかを知りたいこと、または、実際にそれを行った場合に反事実的な結果が得られることを期待することを意味します。過去 違う行動をとったら、未来は変わるでしょうか?ただし、現実の世界で反事実データを観察したり収集したりするのが難しいことが多いのが難点です。
この記事では、因果推論の 2 つの学派、ルービン因果モデル (RCM; Rubin 1978) と因果関係図 (Pearl 1995) ) の主要な技術的アイデアと、近年の新しい手法やアプリケーションだけでなく、著者の学歴は比較的計量経済学に関連しているため、引用した手法や論文は主に経済文献を参照しており、理論の深さと幅広さ、手法の応用については一部省略している部分があるかもしれませんが、ご容赦ください。
潜在的な結果モデル
i を使用して各研究対象またはユーザーを表し、これらは特定の戦略的介入の対象となる可能性があります: Ti=1 は次のことを表します。介入 (実験グループ)、Ti=0 は介入なし (ベースライン グループ) を表し、注目する対応する結果は Yi0 です。 と Yi1 ですが、実際に発生する状況は 1 つだけです。つまり、Yi0 と Y# です。 ##i1そのうちの 1 つだけが観察でき、もう 1 つは不明です。ここで期待する因果推論結果は、平均治療効果 ATE=E[Y1-Y0] です。
ATE を推定することの難しさは、特定の数学的導出によって説明できます。 Yi0 と Yi1 のいずれか 1 つだけを観察するので、何が起こるか実際に直接計算できるのは、実験グループとベースライン グループの間のグループ間差 E[Yi1|Ti##=1]-E[Yi0|Ti #=0], この差は、さらに E[Yi1# に等しく分解できます。 ##|Ti##=1]-E[Yi0 #|Ti=1] E[Yi0|T i=1]-E[Yi0|Ti =0]。ここで E[Yi1|Ti=1]-E[ Yi0|T#i=1] は、次の個人にあります。実験グループの平均治療効果 (ATT)、ATT と ATE は等しくないことが多く、この 2 つの差が、我々が計算する外部妥当性 (外部妥当性) を表します。サンプルが特定の年齢層のユーザーに限定されている場合、結果はすべての年齢層のユーザーに一般化できない可能性があり、分析に外部妥当性がない可能性があることを示しています。上記の式の 2 番目の部分 E[Yi0|Ti =1]-E[Yi0|Ti=0]サンプル選択のバイアスを表します。選択バイアスは現実には 0 にならないことがよくあります。たとえば、実験グループとベンチマーク グループがランダムにサンプリングされておらず、特定の特徴分布に違いがある場合、選択バイアスが発生する可能性があります。したがって、私たちが計算したグループ間の差は、選択バイアスが排除され、外部妥当性があり、大規模で十分なサンプルに基づいている場合にのみ、実際に期待される平均治療効果を表します。潜在効果モデルの思考方法は、実際には、特定の設定とモデルを通じてそのような条件を達成することです。そのアイデアの背後には、比較的厳密な数学的前提もあります。以下では、主要なアイデアと、さまざまな手法に基づいた近年の技術開発と応用をレビューしますが、紙面の都合上、ブレークポイント回帰手法についてはここでは詳しく紹介しません。 1. A/B テスト
潜在効果モデルの最も一般的な方法業界で一般的に使用されるランダム化された実験、または A/B テストです。グループ間の違いを観察するために、特定のランダムサンプリングを通じて実験グループとベースライングループを構築しました。ただし、たとえランダム性が満たされたとしても、ここでの因果推論の有効性は依然として重要な仮定、つまり安定単位治療値仮定 (SUTVA) を満たす必要があることを指摘しておく必要があります。各個人の潜在的な結果は、その人自身にのみ関連しており、他の個人が実験戦略によって介入されるかどうかとは何の関係もありません。同時に、私たちが懸念している単一の戦略的介入には、結果につながるさまざまな形式や強度はありません。さまざまな潜在的な結果。現実には、SUTVA の前提に違反するシナリオが数多くあります。これは、混雑問題に対する予算や戦略的な制御、または迂回設計の改善など、さまざまな新しい A/B テスト手法の開発にも影響を与えています。ここでは、流用に関連するいくつかの例を示します:
LinkedIn では、実験者がネットワーク サンプリング実験手法を使用して、ソーシャル ネットワークが従来の個別のランダム実験にもたらす課題に対処しています。まず、ユーザーを異なるクラスターに分割し、各クラスターを個人としてランダムに分割して実験指標を測定し、推定された治療効果はユーザーのネットワーク効果エクスポージャーを推定することで補正されます (Gui et al. 2015)。
Airbnb などのプラットフォームでは、買い手と売り手の間に相互影響が存在することが多く、これが従来の実験手法を妨げる可能性もあります。研究者は、双方向実験計画とインベントリの動的モデルを通じて実験評価指標を構築します(Johari et al. 2022)。双方向実験は比較的新しい分野であり、その実験デザインは、実験者が従来の一方的実験の波及効果を発見するのに役立ちますが、実験結果の統計的な推論と修正を行うのは困難であり、実験結果を統計的に推論することは困難である可能性があることを指摘しておく必要があります。絶対的な答えですが、ビジネスシナリオと組み合わせてさらに議論する必要があります。
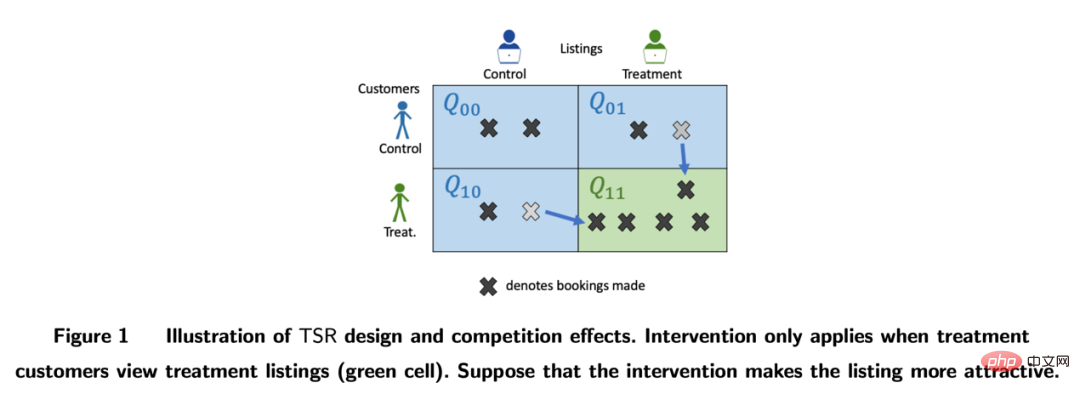
論文からの画像 Johari et al. (2022)
2, 操作変数法
操作変数は線形回帰の内生性問題を解く手法です。次に、内生性の問題と、操作変数を通じて内生性を解決する方法を紹介します。内生性に関する主な問題は、X が Y に及ぼす影響を考慮しているのに、X と Y の両方に影響を与える未測定の変数 U が存在する場合です。この場合、X は内生変数、U は前述の交絡変数です。 X に関連する変数 Z が見つかり、Z が U に関連していない場合。次に、Z を操作変数として使用して、X の Y に対する因果効果を推定します。具体的な計算方法は、一般に 2 段階の最小二乗法です。実際に操作変数法を使用する場合は、「弱い操作変数」の問題、つまり操作変数 Z と注目変数 X の相関が非常に低く、結果に偏りを引き起こす可能性があることに注意する必要があります。推定された因果関係。そのような問題が存在するかどうかを確認するには、統計的検定方法が信頼できます。
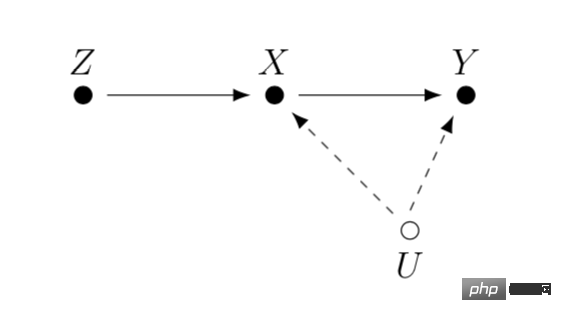
#操作変数手法の開発の 1 つは、ハートフォードによって提案された深層学習モデルと組み合わせることです。 et al. (2017) Deep IV メソッド。この研究は、従来の操作変数の 2 段階最小二乗法を 2 つのディープ ニューラル ネットワークのより柔軟な予測タスクに変換し、従来の方法におけるデータ生成プロセス (DGP) に関する強い仮定を緩和します。
#実際のアプリケーションでは、インターネット上の多数のA/Bテストで蓄積されたシナリオをもとに、実験的なメタ学習を通じて指標を学習することができます。と操作変数メソッド間の因果関係。たとえば、Peysakhovich & Eckles (2018) は Facebook データを使用し、実験グループの情報を操作変数として使用し、2 段階の最小二乗法に基づいて L0 正則化を組み合わせました。これにより、従来の操作変数のバイアス問題を解決できます。限られたサンプルを対象とした手法であり、現実世界の状況での多数の実験で観察される効果の絶対値が比較的低い (「弱い操作変数」) という問題も克服できます。
指標間の影響関係を学習することに加えて、操作変数の考え方は、レコメンデーション システムにおけるバイアスの問題を解決するためにも使用できます。レコメンデーション システムでは、モデルのトレーニングは多くの場合、ユーザーの履歴ビューやいいね! のフィードバック行動に依存しますが、これらの履歴データは、表示場所や露出モードなどの交絡要因の影響を受けることがよくあります。Kuaishou と人民大学 Si et al. の研究者 (2022)は、操作変数のアイデアを使用した IV4Rec フレームワークを提案し、検索クエリを操作変数として使用して、推奨システムの埋め込みにおける因果関係と非因果関係を分解します。深層学習と組み合わせると、Kuaishou データと非因果関係の両方で使用できます。公開データセットMINDを活用し、推奨モデルの改善効果を検証します。
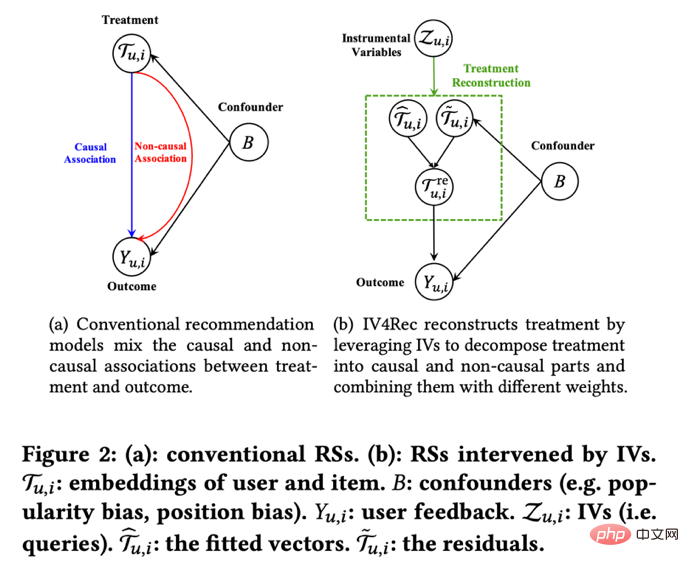
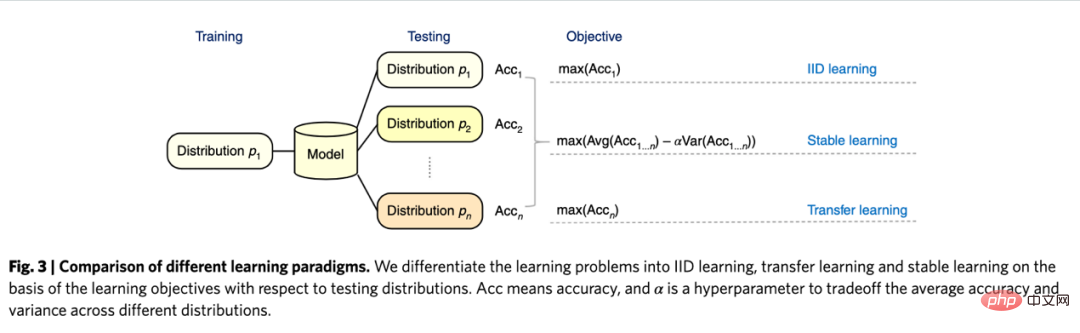
写真は Si らの論文 (2022) から引用しました。 マッチングは、ビジネスで広く使用されている因果分析手法であり、主に問題が発生した場合に問題を解決するために使用されます。実験グループと対照グループが何らかの理由で比較できない場合 (交絡因子)、実験グループの各ユーザーは、特定の特性 (CEM 粗粒度マッチング) または介入を受け入れる確率 (傾向) において最もよく似ているユーザーと照合されます。スコア) ) 最も類似した (PSM 傾向スコア マッチング) コントロール グループ ユーザーを抽出し、比較可能な実験グループとコントロール グループを再作成します。マッチングはAB/RCT(ランダム化比較試験)のランダム実験に最も似た手法で、操作方法も比較的似ており、結果も非常に直感的です。さらに、マッチングは治療効果を推定するノンパラメトリックな方法であり、一般的な線形パラメトリック モデルの仮定の影響を受けません。サンプルをマッチングすることで、新機能の普及率が低い問題を解決するためによく使用される二重差分法も使用できます。近年、傾向スコアのマッチングをより正確にするために、主に機械学習モデルと組み合わせたマッチング手法の開発が行われていますが、同時に、ここでの考え方は他のいくつかの因果関係手法や機械学習モデルの修正にも適用されています。内容については後述します。 近年、パネルデータの因果推論には多くの新しい方法があります。まず、従来のパネル データ手法を確認してみましょう。 #最も一般的に使用される方法は、二重差分法です。最も単純な差分の差は、グループ間の差を制御し、それを回帰モデル yit=α0 α## の形式で記述することです。 #1治療 i α2投稿 t α3治療 i*投稿 。ここで、Treati#=1 は、個人が介入されたかどうかを表します。 #= 1 は介入後の観察期間を表します。次の表から、α2 α3 が次のとおりであることがわかります。実験群 実験日前後の差分値、α2 は、対照群の実験日前後の差分値です。これら 2 つの項目の差により、α3 は因果効果の推定値であり、上記のモデルの交互作用項の係数でもあります。は 2 つの違いの結果です。 #差分法は、比較的厳密な仮定に基づいています。 「平行傾向」は最も重要な前提であり、政策介入前の実験群とベンチマーク群のアウトカム指標の平均値は時間の経過とともに安定しており、これは政策以外の他の要因の影響が少ないことを示している。介入自体は実験群でもベンチマーク群でも同じです。時間傾向プロットを使用して並列仮説をテストでき、一部の統計的推論パッケージも対応する関数を提供します。並列テストが失敗した場合は、回帰に制御変数または時間傾向項を追加することで、さらなるテストを実行できます。場合によっては、三重差分法の助けを借りて解決することもできます。さらに、実際には、二重差分法を実装する方法は数多くあります。上記の方法以外に、「双方向固定効果モデル」の設定も採用可能です。 Y it Xit β αi ξt εit, ただし、強力な仮定にも依存しています。つまり、変化する交絡因子はありません。過去の実績が現在の治療状況に影響を与えず、政策の治療効果も変わらないことが求められます。その背後にある理論と手法の限界、およびマッチングや再重み付けなどの拡張された新しい手法については、スタンフォード大学の Xu Yiqing 教授が教えるコースと併せて学習することをお勧めします。 ## https://yiqingxu.org/teaching/ ここでは、より一般的に使用されるもののいくつかをリストします。新しいメソッド: 総合制御法は、パネルデータの因果推論法から派生した一連の手法であり、新しい推定または統計的推論の検証研究が常に登場しています。グループまたは地域で介入が実施される場合、実験グループは 1 つの時点で 1 つの観測値しか持たず、地域のプロモーション活動を行っている都市など、データの期間が長くなります。差分法は適していませんが、現時点では合成制御法を採用することができます。原理は、いくつかの対照都市を選択し、それらを介入前の実験グループに非常によく似た「仮想対照グループ」に当てはめることです。近年の詳細な理論的導入と最適化については、米国のアベルト・アバディ教授の研究を参照してください。マサチューセッツ工科大学とその共同研究者による論文 (Abadie、Diamond、Hainmueller 2010) およびさらなる研究のための NBER での短期コース: https:// www.nber.org/lecture/2021-Summer-institute-methods-lecture-alberto-abadie-synthetic-controls-methods-and-practice 二重微分法と合成制御 実際、すべての法則は一連の分析フレームワーク システム内で統一できます。 Arkhangelsky et al. (2021) による研究では、差分の差分は個人や時間の重み付けを行わずに二元固定効果回帰問題を解決するのに対し、合成制御法は政策介入が行われる前に個人に重み ω を適用して適合することを指摘しました。この論文は、個人の重み ω と時間の重み λ の両方を含む合成二重差分 (SDID) という 2 つの方法を組み合わせて新しい推定量を提案し、推定量全体のロバスト性を向上させます。ここでの時間重み λ は、介入後の期間に類似するデータ期間に高い重みが与えられると理解できます。 いくつかの方法の比較: Arkhangelsky et al. の論文からの画像 ( 2021) パネル データをマトリックス補完手法と組み合わせて因果推論を行うこともできます。これは、この分野における近年の新しい開発でもあります。行列補完アルゴリズムは、凸最適化問題を解くことによって、因果推論が直面する反事実データの欠落の問題を解決します。この方法は、個人が一貫性のないポリシー介入時間にさらされる状況に適しています。たとえば、製品を反復して有効にするためにはユーザーが製品バージョンを更新する必要があるが、ユーザーの更新時間が一貫していない場合などです。詳細な方法理論については、Athey et al. (2021) などの関連論文を参照してください。ランダム介入下での行列補完、合成制御、回帰予測手法も最適化問題の枠組みで統合することができ、複数の手法をアンサンブル方式で組み合わせて、よりロバストな推定結果を取得することもできます (Athey et.al 2019) 。 マトリックス完成図: この図は AEA の Guidon Imbens のコースからのものです。W は治療ステータスを表します https: //www.aeaweb.org/conference/cont-ed/2018-webcasts 上記のこのセクションでは、パネル データの因果関係の主な方法を紹介しました。推論と進歩というように、この分野は非常に多様な手法があり、進歩も早い分野ですが、実際にさまざまな政策をより正確に評価するためには、手法の背後にある前提や限界について利用者が十分に考える必要があります。スペースの制限があるため、ここでは非常に簡単な紹介のみを行います。 機械学習との組み合わせ異種因果関係の研究は、実際、近年の因果推論の開発におけるトレンドです。まず不均一因果効果を紹介しましょう。不均一処理効果 (HTE) とは、サンプルの異なる個々の特性により、実験が個人に異なる効果をもたらす現象を指します。数式と組み合わせて表現すると、HTE にはさまざまな形式があります: 各個人の因果効果 ITE (個人治療効果): τi=Yi1-Yi0、Y 1 つだけi1 と Yi0 の 2 つは観測できますが、もう 1 つと τi は特定のモデル手法を通じて推定する必要があります。 特定の特性に対するグループの平均因果効果。ここでは特性を表すために X を使用します。その場合、推定される CATE (条件付き平均治療効果) は制限されます。特性の特定の値を持つ母集団に対する平均因果効果: τ(x)=E[Y1-Y0|X=x]。 #HTE の分析手法には現在、幅広い応用シナリオがあります。 HTE を通じて、特定の戦略的介入に最も反応するグループの特徴を知ることができ、A/B テスト戦略のメカニズムを調査する際に、期待される効果があるか、効果がないのかを調査するのにも役立ちます。戦略の中のさまざまなパーソナライゼーションに適用されます。異種因果関係推論手法は、業界やインターネットで多くの応用例があります。たとえば、トリップアドバイザーは会員登録インセンティブの測定に使用されています。マイクロソフトは、この手法と短期データを使用して、さまざまなプロジェクトの長期 ROI を測定しています。詳細な応用例は次のとおりです。 2021 年度 KDD トレーニング コース (https://causal-machine-learning.github.io/kdd2021-tutorial/) を参照してください。 #不均一因果関係の最も一般的な方法は、実際には実験分析で一般的に使用される多次元分析ですが、多次元分析の使用には次の問題に対する注意が必要です。複数のテスト。同時に、十分な寸法がある場合、実験サンプル サイズに対する要件が比較的高く、分析効率は比較的低くなります。機械学習手法は、効率を向上させるためのいくつかのマイニング手法を提供します。その利点は、異種因果関係の分布を適応的に学習でき、厳密な関数形式の仮定を必要としないことです。線形回帰に基づく従来の計量経済手法よりも優れています。または多次元分析です。方法はより強い自由度を持っていますが、技術的な課題は統計的推論をどのように行うかです。近年、機械学習と計量経済学の組み合わせの深化に伴い、この分野では多くの手法が考案され、応用されていますが、ここでは以下の手法に焦点を当てます。これらの手法の基本的な前提はすべて条件付き独立性の仮定です。 (条件付き独立性の仮定)、つまり、さまざまな交絡変数が十分に制御されている場合にのみ、因果効果の比較的正確な推定値を取得できます。 コーザル フォレスト: ランダム フォレストに基づいて、フィッティング推定を直接実行するノンパラメトリック手法です。因果ツリーの主な推定ロジックは、各葉に対する因果効果を定義することによってツリー全体の損失関数を定義することです。因果ツリーは、X を分割する特定の方法に従って、すべての葉の損失の合計を最大化することを目的としています。機械学習のツリー アルゴリズムとは異なる推定目標に加えて、因果推論アルゴリズムでは、トレーニング セットのサンプルが一般にトレーニング セットと推定セットに分割されるという違いもあります。トレーニング セットはリーフ分割に使用され、推定セットはリーフ分割に使用されます。葉を切った後の各葉ノードに対する平均処理効果を計算します。因果関係ツリーの利点は、結果が非常に簡潔で理解しやすいことです。バケット化を通じて、実験効果に明確な違いがある人々のグループを直接特定できます。多くの場合、最初にバケット化された指標が因果効果の差の最大の次元になります。 。ただし、因果ツリーは過学習になりやすいため、実際の作業では因果ランダム フォレストを使用することをお勧めします (詳細については、Athey and Imbens 2016、Wager and Athey 2018 を参照してください)。統計的推論のプロパティ。この手法の拡張については、Athey, Tibshirani and Wager (2019) や Friedberg et al. (2020) などの研究成果を参照してください。これらの新しい手法は、交絡変数がある場合の問題にさらに対処し、結果をよりスムーズに推定できます。 。 メタ学習者: 因果ツリーを使用して因果効果を直接推定するモデルとは異なり、これは間接推定モデルの一種です。結果変数 Y を直接モデル化します。したがって、メタ学習器は推定された HTE を統計的推論に直接使用することはできませんが、実際のアプリケーションでは、一部の研究者はブートストラップを使用してこの問題を解決します。メタ学習者の推定アルゴリズムには、T-Learner、S-Learner、X-Learner の 3 種類があります。 3 つの方法の基本的な違いは次のとおりです。 最も単純なのは S-learner です。介入変数を 1 回限りのモデリングの特性変数として使用します。これは、治療変数と結果変数に強い相関がある状況に適しています。そうでない場合、モデルは、介在変数の変化によって引き起こされる結果の変化を識別できません。 少し複雑なものは T-learner です。 2 つのモデルに実験グループの Yi1 と対照グループの Yi0 をそれぞれ学習させることで因果効果を特定します。実験に多くの変数がある場合の使用に適しています。グループとコントロール グループ、およびより平均的なモデルを使用する場合、モデルの 1 つがより正規化されます。 XX 学習者は、2 つの方法を使用する比較的新しい方法です。ステップ 傾向スコアを推定して使用してバイアスを修正すると、データ量が少ない場合に、より適切な推定を行うことができます (詳細については、Künzel et al. 2019 を参照)。 DML と DRL に基づく見積もりフレームワーク: これら 2 つのフレームワークを Microsoft の Econml ツールと組み合わせて紹介します: https://www.microsoft.com/en-us/research/project/econml/ ##DML (Double Machine Learning) デュアル機械学習は、高次元の交絡変数の存在下で、変数、処理変数、結果変数間の関係を柔軟に混同するフレームワーク手法であり、その名のとおり因果関係を推定します。効果は主に 2 つのステップに分かれています。最初のステップでは、2 つの (必ずしも同じではない) 機械学習モデルを使用して、2 つの条件付き期待値 E(Y|X,W) と E(T|X,W) をそれぞれ推定します。次に残差を受け取ります。ここで、X と W は両方とも交絡変数ですが、CATE では X のみが関連変数です。第 2 ステップは残差に基づいて ATE または CATE を推定することであり、CATE を推定する場合、T-E(T|X,W) の残差に X に関する関数 θ(X) を乗じて推定します。 ATE の推定方法については、Chernozhukov et al. (2018) を参照してください。 Econml は、2 番目のステップで選択できる多くのモデルを提供します: LinearDML (OLS モデルを使用)、DML (カスタム モデルを使用)、CausalForestDML (因果関係のあるランダム フォレストを使用)... DML フレームワークを使用する場合は、2 つのモデルの残差項の平均が 0 から大きく乖離していないか、有意な相関があるかどうかを確認する必要がありますが、そうであれば、交絡変数が十分に制御されていない可能性があります。 DRL フレームワークは、二重ロバスト方式に基づいており、これも 2 つのステップに分かれています。最初のステップでは、X、W、T を使用して Y、そして予測値を gt(X,W) として定義します; 2 番目のステップでは、分類モデルを使用して X と W を使用して T を予測し、次の結果を取得します。傾向スコア。pt(X,W) として定義されます。ここでの T は離散変数であり、ある種の回帰ベースのモデル gt(X,W) に制限されることに注意してください。 2 ステップの結果の後、調整された結果変数が計算されます: 続いて調整された Y #i,tDR## 実験グループと対照の間の差異 Y# を見つけますグループ ##i1DR-Yi0DR、X を返して CATE を取得します。 DRL が二重ロバストと呼ばれる理由は、上記の式で gt(X,W) および p であるためです。 t(X, W) の 1 つの推定値が正しい限り、因果効果の推定値には偏りはありません。ただし、両方のモデルの推定値が間違っている場合、結果として生じる誤差は非常に大きくなる可能性があります。 DML と同様に、Econml の DRL のさまざまな学習者の違いは、Yi1DR に適合させるためにどのような種類のモデルが使用されるかです。 #-Yi0DR# #。 機械学習モデルに基づく異種因果推論手法のアプリケーションにおける最大の課題は、実際には、適切な機械学習モデルを選択し、比較的堅牢な推定結果を得るためにパラメータを調整する方法です。アプリケーションの経験と最近の研究に基づいて、次の注意事項があります: 上で紹介した方法は、基本的に、介在変数の下での静的な異種因果効果に焦点を当てています。しかし、実際のアプリケーションでは、より複雑な問題が発生します。たとえば、複数の介在変数が関係します。製品によってユーザーに提供される補助金インセンティブには、サインイン インセンティブと他のタスクに対する報酬の両方が含まれる場合があります。さまざまな種類のインセンティブの配分のバランスをとる方法は、異種因果関係構築として定義できます。複数の介在変数のモデリングと最適化の問題。もう 1 つの例は、動的な因果効果であり、交絡変数が異なる時点での介入によって変化します (Lewis and Syrgkanis 2020 を参照)。インセンティブ タスクを例に挙げると、これらのタスクにより、ユーザーが新しいアンカーに注意を払うようになり、コンテンツの視聴の好みが変わり、その後のインセンティブの効果にも影響を与える可能性があります。これらの複雑なシナリオは、さまざまな手法のさらなる拡張に影響を与えており、将来的にはより確立された体系的な研究と応用が生まれることにも期待しています。 前のセクションでは、潜在的な結果モデルの主要なアイデアと方法論の開発について紹介しました。このタイプの流派手法は統計理論が比較的完成しており、比較的正確な推定結果が得られます。ただし、変数間の相関度 1 の影響を推定する場合にのみ使用できる (つまり、1 つの従属変数といくつかの独立変数のみが許可され、間接的な効果のリンクは推定できない) という制限があります。多くの変数間のリンクと複雑な関係には、別の流派の構造因果モデル手法の使用が必要です。 構造因果モデルは、有向非巡回グラフ (DAG) を使用して、変数間の因果関係と条件付き分布を記述します。グラフの各ノードは変数であり、因果関係はこれらのノードを結ぶエッジによって表されます (例: X1#)。 # #2 は、X2 を表し、X1# に影響を与えます##、X1 を子ノード、X2## とも呼びます。 # 親ノード。一連の確率変数 X=(X1,X2,. .. .,X##P)、変数の結合分布は、P(X)=∏p# として表すことができます。 ##j=1P(Xj|paj)、paj は、Xj# のすぐ隣です。 ## の親ノード。因果関係を表現する場合、現在の X=(X1,X 2 と仮定して、do 演算子の概念を導入します。 ,...Xp)=(x1,x2,...xxp)、使用しますdo(Xj=x'j) 変数 X## を表します#j 介入 (xx'j に割り当て) を実行すると、変数間の条件付き分布関係を使用できます。新しい DAG: P(X1=x1,X2=x2,...,Xp #=xp|do(Xj =xx'j))、古い分布と新しい分布の下での他の変数の予想される変化は、XXj# です。 ##それらに対する因果関係 (E(X1|do)(Xj など) =x'j)-E(X1| (Xj=xj)) を実行します。アウトカム因果モデルの創設者であるユダヤ・パール氏は、因果関係を特定するために因果図を使用する場合、「バックドア基準」と「フロントドア基準」が満たされていれば、実際にはすべての変数を観察する必要はない、と研究の中で指摘しました。具体的な理論的な詳細については、Pearl (2009) を参照してください。構造的因果モデルと潜在的結果モデルは実際には関連していることを付け加えておく必要があります。 実際のアプリケーションでは、因果グラフを定義するための情報が直接得られない可能性があるため、変数間の因果グラフ構造をどのように学習するかが重要な問題になります。このタイプの問題を解決するときは、まず必要な仮定を明確にする必要があります。 因果マルコフ 因果マルコフ仮定: この仮定は、任意のノードの条件付き分散は、その直接の親ノードのみに基づきます。 因果十分性の仮定: この仮定は、観察できない交絡変数が存在しないことと同じです。 因果忠実度因果忠実度の仮定: この仮定は、いくつかの条件付き確率分布に基づいて、一部のノードが独立していることを意味します (したがって、グラフはカットされます)。 アルゴリズムは大きく 2 つのカテゴリに分類されます。 詳細な紹介については、こちらをご覧ください。 Glymour、Zhang、Sprites (2019) および 2018 年の「Science China: Mathematics」第 12 号の記事「因果推論の統計的手法」を参照してください: # #https://cosx.org/2022/10/causality-statistical-method/ 。 制約ベースのアルゴリズム: 条件付き分布に依存しないテストに基づいて、条件を満たすすべてのパラメーターを学習します。忠実性と因果的マルコフ仮定 因果図、つまり 2 つのノード間の条件付き分布が独立しているかどうかをテストします。たとえば、PC アルゴリズム (Spirtes および Glymour 1991) および IC アルゴリズム (Verma および Pearl 1990) です。 スコアベースのアルゴリズム: 特定のスコアで定義されたグラフ構造を最適化することで、データに最も一致するものを見つけます。 。構造方程式とスコア関数を定義する必要があります。たとえば、CGNN アルゴリズム (Goudet et al. 2017) や NOTEARS アルゴリズム (Zheng et al. 2018) です。ここでは、NOTEARS アルゴリズムに焦点を当てます。従来のアルゴリズムは、すべてのノードとノード間の考えられる関係に基づいており、すべての考えられるグラフを検索し、特定の基準に従って最適解を選択します。これは典型的な NP 困難問題であり、多くの時間がかかります。長年にわたる現在のコンピューティング リソースでは、基本的にコンピューティングのニーズを満たすことができません。 NOTEARS アルゴリズムは、離散探索問題を連続探索問題に変換します。このアルゴリズムにより、計算速度が大幅に向上し、一般のデータ アナリストが使用できるようになります。ただし、この方法には一定の制限もあります。たとえば、すべての変数のノイズはガウス分布でなければならないと仮定されています。近年、ますます多くの方法 (He et al. 2021 など) が次の仮定を改善しようとしています。そのような方法。 #強化学習の分野の発展に伴い、因果推論と強化学習を組み合わせて互いの発展を促進できることもわかりました。 。因果推論は、強化学習における状態間または状態とアクションの間の因果関係を推論することにより、強化学習アルゴリズムが価値関数や最適な戦略をより効率的に学習するのに役立ちます。この側面に興味のある読者は、コロンビア大学のエリアス・バレインボイム教授を参照してください。 https://www.php.cn/link/ad16fe8f92f051afbf656271afd7872d)。一方、強化学習は、ファーウェイのノアの方舟研究所の Zhu、Ng、Chen (2019) など、因果グラフの学習アルゴリズムに統合することもできます。 因果推論の今後の展望については、近年のグラフ学習、因果推論、機械学習に関連した新たな研究パラダイムとして、研究チームが提案した「安定学習」について言及する必要があります。清華大学の崔鵬教授のコンセプト(Cui and Athey 2022)。機械学習や人工知能などのモデルの適用は、独立かつ同一に分散されているという重要な前提に依存しています。つまり、トレーニング セットとテスト セットは同じディストリビューションに由来する必要がありますが、実際にはさまざまな OOD (Out Of Distribution、分布外) 問題があり、現時点ではモデルのパフォーマンスは保証できません。これは歴史上のさまざまなモデルが直面した問題でもあり、重要な技術的リスクです。因果推論は、このような問題を解決するのに役立ちます。 OOD 問題を克服するために、構造がさまざまな環境で同じ予測効果を持つことが保証できる場合、この構造は因果構造である必要があり、さまざまな環境における因果構造のパフォーマンスは比較的安定しています。 Cui Peng氏のチームによる研究(He et al. 2022、Shen et al. 2021)では、交絡変数のマッチングバランスのアイデアを使用することで、サンプルの重み付けを変更することですべての変数を独立させ、相関ベースのモデルを作成できることがわかりました。原因と結果に基づいたモデル。いわゆる安定学習では、1 つの分布のトレーニング セットと複数の異なる未知の分布のテスト セットを使用し、最適化の目標は精度の分散を最小限に抑えることです。これは将来的に非常に重要な分野であると思いますので、興味のある読者は関連する研究の進歩に引き続き注目してください。 独立した同一分散学習、転移学習、安定した学習の比較: 論文 Cui and Athey 2022 の画像 レコメンデーションシステム、コンピュータビジョン、自動運転、自然言語処理などの機械学習や人工知能関連分野は、実際の応用においては因果関係に満ちています。推論と因果グラフ学習はこれらの分野の発展を促進しました. ここでは近年の例もいくつかリストします. 機械学習に関連するより詳細なアプリケーションとベンチマークシミュレータとデータセットについては, UCLとUCLの研究者の概要を参照してください.オックスフォード大学 (Kaddour et al. 2022)。レコメンドシステムの分野では、操作変数手法の応用でも紹介したように、レコメンドシステムには必然的にバイアスが発生しますが、ユーザーとアイテムの因果関係をグラフで特定することで、レコメンドシステムのバイアスを修正することができます。たとえば、Wang et al. (2021) と Zhang et al. (2021) は、それぞれクリックベイトと人気によって引き起こされるバイアスを排除するために因果関係図を使用しました。自動運転の分野では、Microsoft の研究者らが、因果推論を車両軌道予測に統合する模擬運転環境プラットフォームである CausalCity (McDuff et al. 2022) を立ち上げました。自然言語処理の分野では、研究者らは、言語モデルとコーパスにおけるバイアスのテスト (Vig et al. 2020) を含め、因果推論が NLP 手法をより堅牢で理解しやすくするのに役立つことを発見しました (Zeng et al. 2020)。将来的には、因果推論が今後も繁栄し、これらの分野やその他の分野で重要な役割を果たすと信じています。 3, マッチング手法
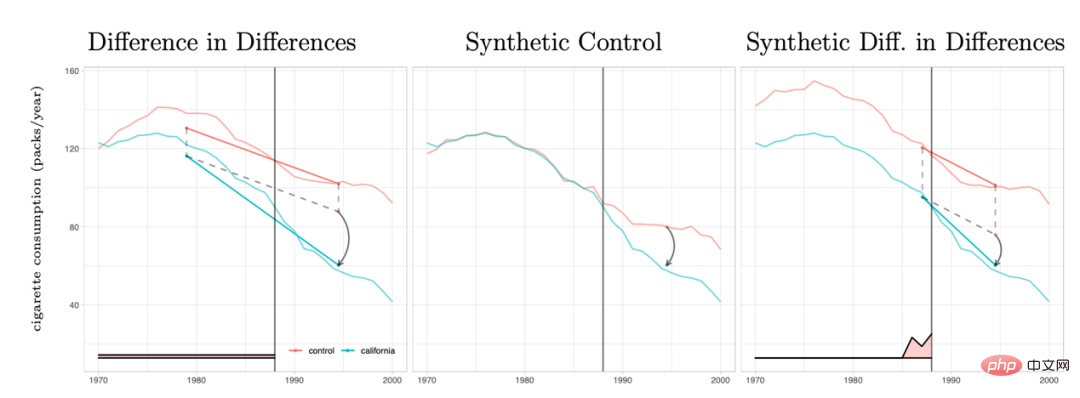
4, シリアル手法とパネルデータの開発
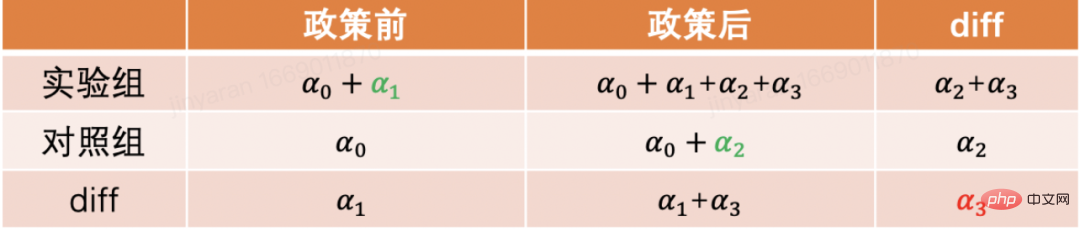 =τTreat
=τTreat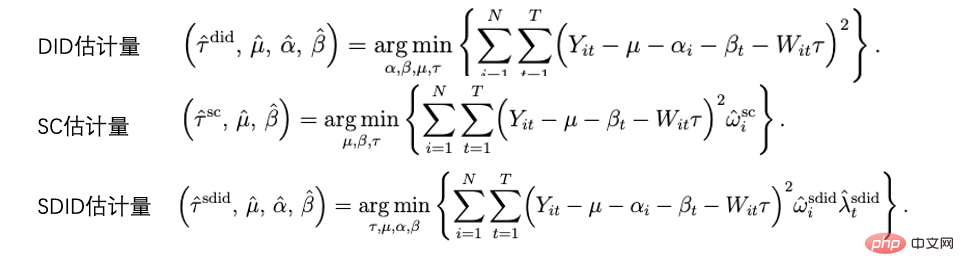

#5, 異種因果関係の手法のレビュー
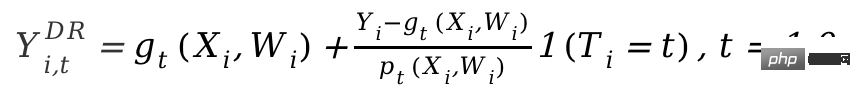
https://github.com/uber/causalml 。
構造因果モデル
以上が主な技術思想と因果推論手法の概要の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7490
7490
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 41
41
 CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: BEVFormer 構造を明示的に監視して、ロングテール検出パフォーマンスを向上させます。
Mar 26, 2024 pm 12:41 PM
上記および筆者の個人的な理解: 現在、自動運転システム全体において、認識モジュールが重要な役割を果たしている。道路を走行する自動運転車は、認識モジュールを通じてのみ正確な認識結果を得ることができる。下流の規制および制御モジュール自動運転システムでは、タイムリーかつ正確な判断と行動決定が行われます。現在、自動運転機能を備えた自動車には通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなどのさまざまなデータ情報センサーが搭載されており、さまざまなモダリティで情報を収集して正確な認識タスクを実現しています。純粋な視覚に基づく BEV 認識アルゴリズムは、ハードウェア コストが低く導入が容易であるため、業界で好まれており、その出力結果はさまざまな下流タスクに簡単に適用できます。
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の基礎となる原則とアルゴリズムの選択を調べる
Apr 02, 2024 pm 05:36 PM
C++sort 関数の最下層はマージ ソートを使用し、その複雑さは O(nlogn) で、クイック ソート、ヒープ ソート、安定したソートなど、さまざまなソート アルゴリズムの選択肢を提供します。
 人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能は犯罪を予測できるのか? CrimeGPT の機能を調べる
Mar 22, 2024 pm 10:10 PM
人工知能 (AI) と法執行機関の融合により、犯罪の予防と検出の新たな可能性が開かれます。人工知能の予測機能は、犯罪行為を予測するためにCrimeGPT (犯罪予測技術) などのシステムで広く使用されています。この記事では、犯罪予測における人工知能の可能性、その現在の応用、人工知能が直面する課題、およびこの技術の倫理的影響について考察します。人工知能と犯罪予測: 基本 CrimeGPT は、機械学習アルゴリズムを使用して大規模なデータセットを分析し、犯罪がいつどこで発生する可能性があるかを予測できるパターンを特定します。これらのデータセットには、過去の犯罪統計、人口統計情報、経済指標、気象パターンなどが含まれます。人間のアナリストが見逃す可能性のある傾向を特定することで、人工知能は法執行機関に力を与えることができます
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
 Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
Jiuzhang Yunji DataCanvas マルチモーダル大規模モデル プラットフォームの実践と考察
Oct 20, 2023 am 08:45 AM
1. マルチモーダル大型モデルの発展の歴史 上の写真は、1956 年に米国のダートマス大学で開催された最初の人工知能ワークショップです。このカンファレンスが人工知能開発の始まりとも考えられています。記号論理学の先駆者たち(前列中央の神経生物学者ピーター・ミルナーを除く)。しかし、この記号論理理論は長い間実現できず、1980 年代と 1990 年代に最初の AI の冬の到来さえもたらしました。最近の大規模な言語モデルが実装されて初めて、ニューラル ネットワークが実際にこの論理的思考を担っていることがわかりました。神経生物学者ピーター ミルナーの研究は、その後の人工ニューラル ネットワークの開発に影響を与えました。彼が参加に招待されたのはこのためです。このプロジェクトでは。
 58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
58 ポートレート プラットフォームの構築におけるアルゴリズムの適用
May 09, 2024 am 09:01 AM
1. 58 Portraits プラットフォーム構築の背景 まず、58 Portraits プラットフォーム構築の背景についてお話ししたいと思います。 1. 従来のプロファイリング プラットフォームの従来の考え方ではもはや十分ではありません。ユーザー プロファイリング プラットフォームを構築するには、複数のビジネス分野からのデータを統合して、ユーザーの行動や関心を理解するためのデータ マイニングも必要です。最後に、ユーザー プロファイル データを効率的に保存、クエリ、共有し、プロファイル サービスを提供するためのデータ プラットフォーム機能も必要です。自社構築のビジネス プロファイリング プラットフォームとミドルオフィス プロファイリング プラットフォームの主な違いは、自社構築のプロファイリング プラットフォームは単一のビジネス ラインにサービスを提供し、オンデマンドでカスタマイズできることです。ミッドオフィス プラットフォームは複数のビジネス ラインにサービスを提供し、複雑な機能を備えていることです。モデリングを提供し、より一般的な機能を提供します。 2.58 中間プラットフォームのポートレート構築の背景のユーザーのポートレート 58
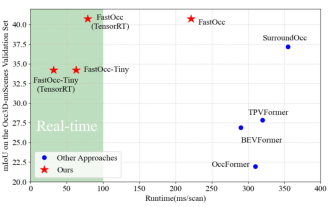 SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
上記と著者の個人的な理解は、自動運転システムにおいて、認識タスクは自動運転システム全体の重要な要素であるということです。認識タスクの主な目的は、自動運転車が道路を走行する車両、路側の歩行者、運転中に遭遇する障害物、道路上の交通標識などの周囲の環境要素を理解して認識できるようにすることで、それによって下流のシステムを支援できるようにすることです。モジュール 正しく合理的な決定と行動を行います。自動運転機能を備えた車両には、通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなど、さまざまな種類の情報収集センサーが装備されており、自動運転車が正確に認識し、認識できるようにします。周囲の環境要素を理解することで、自動運転車が自動運転中に正しい判断を下せるようになります。頭




