11 の一般的な分類特徴エンコード技術

機械学習アルゴリズムは数値入力のみを受け入れるため、カテゴリカルな特徴が見つかった場合は、そのカテゴリカルな特徴をエンコードします。この記事では、11 の一般的なカテゴリカル変数のエンコード方法を要約します。

1. ONE HOT エンコーディング

最も一般的でよく使用されるエンコーディング方法は、One Hot Enoding です。 n 個の観測値と d 個の個別の値を持つ単一の変数は、n 個の観測値を持つ d 個のバイナリ変数に変換され、各バイナリ変数はビット (0, 1) で識別されます。

例:

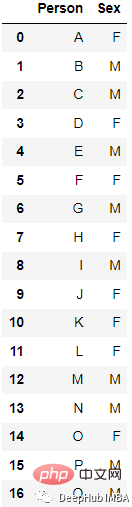
エンコード後

##最も簡単な実装は、pandas の get_dummies # を使用することです。 ##

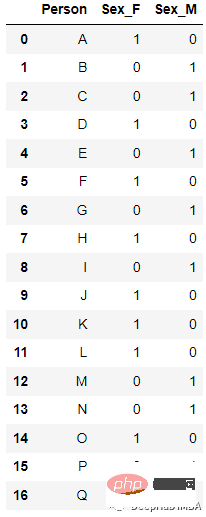
new_df=pd.get_dummies(columns=[‘Sex’], data=df)

2. ラベル エンコーディング

一意に識別された整数をカテゴリ データ変数に割り当てます。この方法は非常に単純ですが、順序付けされていないデータを表すカテゴリ変数では問題が発生する可能性があります。たとえば、高い値を持つタグは、低い値を持つタグよりも高い優先順位を持つことができます。

たとえば、上記のデータでは、エンコード後に次の結果が得られました:

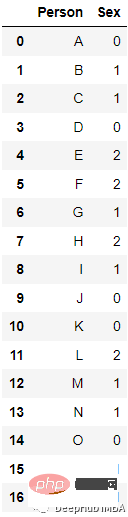sklearn の LabelEncoder は直接変換できます:

from sklearn.preprocessing import LabelEncoder
 le=LabelEncoder()
 df[‘Sex’]=le.fit_transform(df[‘Sex’])

3. Label Binarizer

LabelBinarizer は、複数カテゴリのリストからラベル行列を作成するために使用されるツール クラスです。リストを、一意の値の数とまったく同じ列数の行列に変換します。入力セット内。

たとえば、このデータ

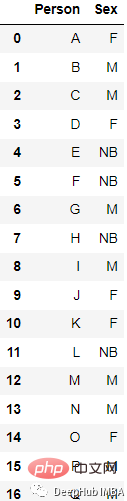変換結果は

##

from sklearn.preprocessing import LabelBinarizer
 lb = LabelBinarizer()
 new_df[‘Sex’]=lb.fit_transform(df[‘Sex’])

4です。1つは省略します。エンコーディング

Leave One Out がエンコードされると、ターゲット カテゴリ特徴変数の同じ値を持つすべてのレコードが平均されて、ターゲット変数の平均が決定されます。エンコード アルゴリズムは、トレーニング データセットとテスト データセットの間でわずかに異なります。分類の対象となる特徴レコードがトレーニング データ セットから除外されるため、これは「Leave One Out」と呼ばれます。

特定のカテゴリ変数の特定の値は次のようにコーディングされます。

ci = (Σj != i tj / (n — 1 + R)) x (1 + εi) where
 ci = encoded value for ith record
 tj = target variable value for jth record
 n = number of records with the same categorical variable value
 R = regularization factor
 εi = zero mean random variable with normal distribution N(0, s)

たとえば、次のデータ:

エンコード後: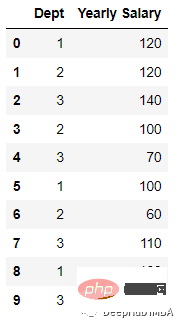

これを実証するにはエンコード プロセスでは、データ セットを作成します: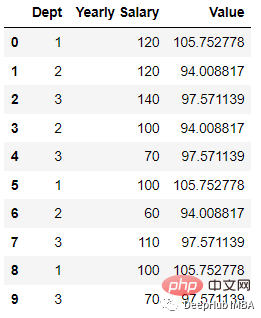

import pandas as pd;
 data = [[‘1’, 120], [‘2’, 120], [‘3’, 140],
 [‘2’, 100], [‘3’, 70], [‘1’, 100],[‘2’, 60],
 [‘3’, 110], [‘1’, 100],[‘3’, 70] ]
 df = pd.DataFrame(data, columns = [‘Dept’,’Yearly Salary’])

そしてエンコードします:

import category_encoders as ce
 tenc=ce.TargetEncoder()
 df_dep=tenc.fit_transform(df[‘Dept’],df[‘Yearly Salary’])
 df_dep=df_dep.rename({‘Dept’:’Value’}, axis=1)
 df_new = df.join(df_dep)

このようにし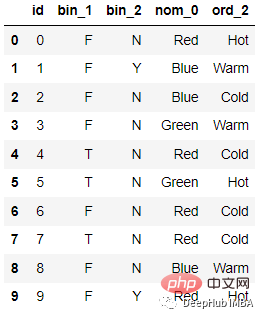て、上記の結果が得られます。

5. ハッシュ

ハッシュ関数を使用すると、文字列は一意のハッシュ値に変換されます。メモリ使用量が非常に少なく、より多くのカテゴリ データを処理できるためです。特徴ハッシュは、機械学習においてまばらな高次元特徴を管理するための効果的な方法です。オンライン学習シナリオに適しており、高速、シンプル、効率的、高速という特徴があります。

たとえば、次のデータ:

エンコード後

コードは次のとおりです。 :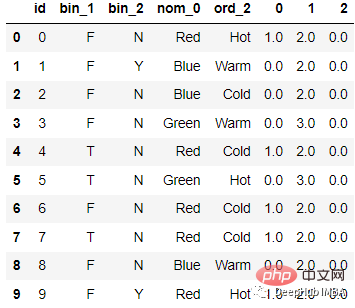

from sklearn.feature_extraction import FeatureHasher
 # n_features contains the number of bits you want in your hash value.
 h = FeatureHasher(n_features = 3, input_type =’string’)
 # transforming the column after fitting
 hashed_Feature = h.fit_transform(df[‘nom_0’])
 hashed_Feature = hashed_Feature.toarray()
 df = pd.concat([df, pd.DataFrame(hashed_Feature)], axis = 1)
 df.head(10)

6. 証拠エンコーディングの重み

(WoE) 開発の主な目標は、クレジットおよび金融業界におけるローン不履行リスクを評価するための予測モデルを作成することです。証拠が理論をどの程度支持または反駁するかは、その証拠の重み、つまり WOE によって異なります。

P(良い) / P(悪い) = 1 の場合、WoE は 0 です。このグループの結果がランダムである場合、P(Bads) > P(Goods)、オッズ比は 1、証拠の重み (WoE) は 0 になります。グループ内で P(Goods) > P(bad) の場合、WoE は 0 より大きくなります。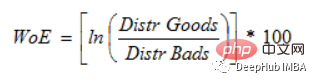

因为Logit转换只是概率的对数，或ln(P(Goods)/P(bad))，所以WoE非常适合于逻辑回归。当在逻辑回归中使用wo编码的预测因子时，预测因子被处理成与编码到相同的尺度，这样可以直接比较线性逻辑回归方程中的变量。

例如下面的数据

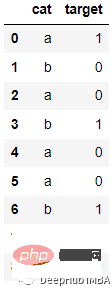
会被编码为：

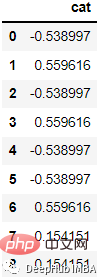
代码如下：

from category_encoders import WOEEncoder
 df = pd.DataFrame({‘cat’: [‘a’, ‘b’, ‘a’, ‘b’, ‘a’, ‘a’, ‘b’, ‘c’, ‘c’], ‘target’: [1, 0, 0, 1, 0, 0, 1, 1, 0]})
 woe = WOEEncoder(cols=[‘cat’], random_state=42)
 X = df[‘cat’]
 y = df.target
 encoded_df = woe.fit_transform(X, y)

7、Helmert Encoding

Helmert Encoding将一个级别的因变量的平均值与该编码中所有先前水平的因变量的平均值进行比较。

反向 Helmert 编码是类别编码器中变体的另一个名称。它将因变量的特定水平平均值与其所有先前水平的水平的平均值进行比较。

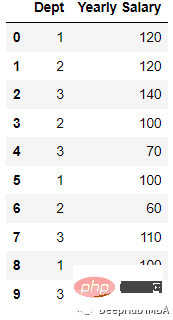
会被编码为

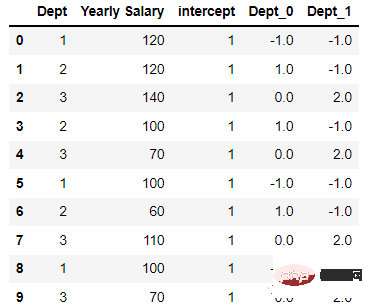
代码如下：

import category_encoders as ce
 encoder=ce.HelmertEncoder(cols=’Dept’)
 new_df=encoder.fit_transform(df[‘Dept’])
 new_hdf=pd.concat([df,new_df], axis=1)
 new_hdf

8、Cat Boost Encoding

是CatBoost编码器试图解决的是目标泄漏问题，除了目标编码外，还使用了一个排序概念。它的工作原理与时间序列数据验证类似。当前特征的目标概率仅从它之前的行(观测值)计算，这意味着目标统计值依赖于观测历史。

TargetCount:某个类别特性的目标值的总和(到当前为止)。

Prior:它的值是恒定的，用(数据集中的观察总数(即行))/(整个数据集中的目标值之和)表示。

featucalculate:到目前为止已经看到的、具有与此相同值的分类特征的总数。

编码后的结果如下：

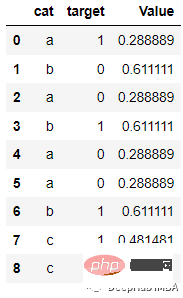
代码：

import category_encoders
 category_encoders.cat_boost.CatBoostEncoder(verbose=0,
 cols=None, drop_invariant=False, return_df=True,
 handle_unknown=’value’, handle_missing=’value’,
 random_state=None, sigma=None, a=1)
 
 target = df[[‘target’]]
 train = df.drop(‘target’, axis = 1)
 
 # Define catboost encoder
 cbe_encoder = ce.cat_boost.CatBoostEncoder()
 
 # Fit encoder and transform the features
 cbe_encoder.fit(train, target)
 train_cbe = cbe_encoder.transform(train)

9、James Stein Encoding

James-Stein 为特征值提供以下加权平均值：

• 观察到的特征值的平均目标值。
• 平均期望值（与特征值无关）。

James-Stein 编码器将平均值缩小到全局的平均值。该编码器是基于目标的。但是James-Stein 估计器有缺点：它只支持正态分布。

它只能在给定正态分布的情况下定义（实时情况并非如此）。为了防止这种情况，我们可以使用 beta 分布或使用对数-比值比转换二元目标，就像在 WOE 编码器中所做的那样（默认使用它，因为它很简单）。

10、M Estimator Encoding:

Target Encoder的一个更直接的变体是M Estimator Encoding。它只包含一个超参数m，它代表正则化幂。m值越大收缩越强。建议m的取值范围为1 ~ 100。

11、 Sum Encoder

Sum Encoder将类别列的特定级别的因变量(目标)的平均值与目标的总体平均值进行比较。在线性回归(LR)的模型中，Sum Encoder和ONE HOT ENCODING都是常用的方法。两种模型对LR系数的解释是不同的，Sum Encoder模型的截距代表了总体平均值(在所有条件下)，而系数很容易被理解为主要效应。在OHE模型中，截距代表基线条件的平均值，系数代表简单效应(一个特定条件与基线之间的差)。

最后，在编码中我们用到了一个非常好用的Python包 “category-encoders”它还提供了其他的编码方法，如果你对他感兴趣，请查看它的官方文档：

http://contrib.scikit-learn.org/category_encoders/

以上が11 の一般的な分類特徴エンコード技術の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。