新しい SOTA を実現するための、変分特徴集約に基づく回帰メタ学習、少数サンプルのターゲット検出
従来の物体検出問題とは異なり、少数ショット物体検出 (FSOD) では、基本的なクラス サンプルは多数あるが、新しいクラス サンプルは少数しかないことを前提としています。目標は、基本クラスから新しいクラスに知識を転送する方法を研究し、それによって新しいクラスを認識する検出器の能力を向上させることです。
#FSOD は通常、2 段階のトレーニング パラダイム # に従います。最初の段階では、検出器は豊富な基本クラス サンプルを使用してトレーニングされ、オブジェクトの位置特定や分類などのオブジェクト検出タスクに必要な一般的な表現を学習します。第 2 段階では、少数 (1、2、3 など) の新規クラス サンプルのみを使用して検出器が微調整されます。ただし、基本クラスと新規クラスのサンプル数の不均衡により、学習されたモデルは通常、基本クラスに偏り、同様の基本クラスを持つ新規クラスのターゲットの混乱につながります。さらに、各新規クラスのサンプルはわずかしかないため、モデルは新規クラスの分散の影響を受けやすくなります。たとえば、複数のトレーニングに対して新しいクラスのサンプルをランダムにサンプリングした場合、結果は毎回大きく異なります。したがって、小さなサンプルの下でモデルのロバスト性を向上させることが非常に必要です。
最近、Tencent Youtu Lab と武漢大学は、変分特徴集約に基づく少数サンプルのターゲット検出モデル VFA を提案しました。 VFA の全体構造は、メタ学習対象検出フレームワーク Meta R-CNN の改良版に基づいており、次の 2 つの特徴集約手法が提案されています。 カテゴリに依存しない特徴集約 CAA (Class-Agnostic Aggregation) And#variational feature aggregation VFA (variational feature aggregation)。
機能集約は FSOD の重要な設計であり、クエリ サンプルとサポート サンプルの間の相互作用を定義します。 Meta R-CNN などの以前のメソッドは通常、クラス固有の集約 (CSA)、つまり、機能集約のための同様のクエリおよびサポート サンプルの機能を使用します。対照的に、この論文で提案されている CAA では、異なるクラスのサンプル間の特徴の集約が可能です。 CAA はモデルがクラスに依存しない表現を学習することを奨励するため、基本クラスに対するモデルの偏りを軽減します。さらに、異なるクラス間の相互作用により、クラス間の関係をより適切にモデル化できるため、クラスの混乱が軽減されます。CAA に基づいて、この記事では、変分エンコーダー (VAE) を使用してサポート サンプルをクラス分布にエンコードし、学習された分布から新しいサポートをサンプルする VFA を提案します。 。関連研究 [1] では、クラス内の分散 (外観の変動など) はクラス間で類似しており、共通の分布によってモデル化できると述べています。したがって、基本クラスの分布を使用して新しいクラスの分布を推定することができ、それによってサンプルが少ない場合の特徴集約の堅牢性が向上します。
VFA は、複数の FSOD データ セットで現行の最良モデルよりも優れたパフォーマンスを発揮します。関連研究が口頭発表として受理されました by AAAI 2023。

VFA モデルの詳細
より強力なベースライン手法: Meta R-CNN現在の FSOD の作業主に次のことが考えられます。メタ学習に基づく手法とファインチューニングに基づく手法の 2 つのカテゴリに分類されます。いくつかの初期の研究では、メタ学習が FSOD に効果的であることが実証されましたが、最近では微調整ベースの手法がますます注目を集めています。
この記事では、まず、メタ学習に基づいたベースライン手法であるメタ R-CNN を確立します。これは、2 つの手法間のギャップを狭め、一部の指標では微調整に基づく手法をさらに上回ります。 。 最初に、メタ学習メソッド Meta R-CNN [2] と微調整ベースのメソッド TFA [3] を取り上げて、2 つのメソッド間の実装におけるいくつかのギャップを分析しました。どちらの方法も 2 段階のトレーニング パラダイムに従っていますが、TFA では微調整段階で追加のテクニックを使用してモデルを最適化します。
- TFA は、モデルが少数ショット カテゴリに過剰適合しないように、ほとんどのネットワーク パラメーターをフリーズし、最終的な分類層と回帰層のみをトレーニングします。
- TFA は、分類層をランダムに初期化する代わりに、基本クラスの事前トレーニングされた重みをコピーし、新しいクラスの重みのみを初期化します。
- TFA は、線形分類器の代わりにコサイン分類器を使用します。
TFA の成功を考慮して、私たちは Meta R-CNN を構築しました。以下の表 1 に示すように、微調整段階を注意深く処理する限り、メタ学習手法でも良好な結果を達成できます。したがって、この論文ではベースライン手法として Meta R-CNN を選択します。
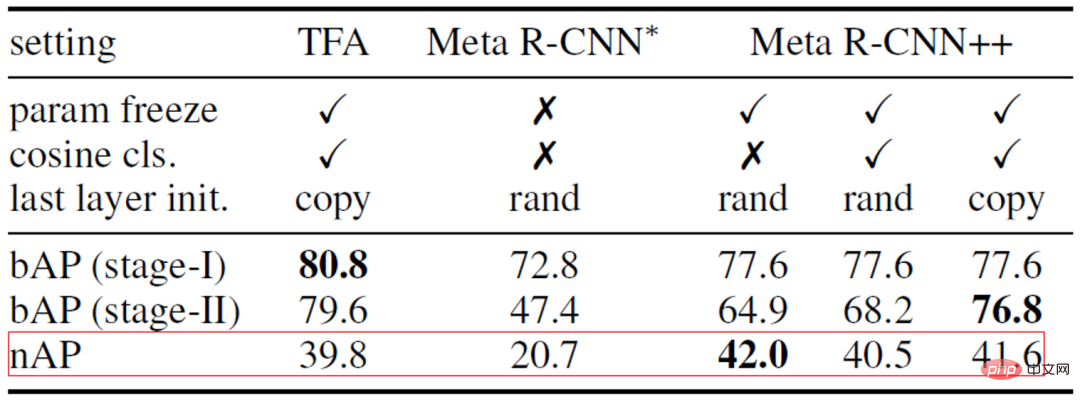
表 1: Meta R-CNN と TFA## の比較と分析
#カテゴリに依存しない特徴量の集約 CAA
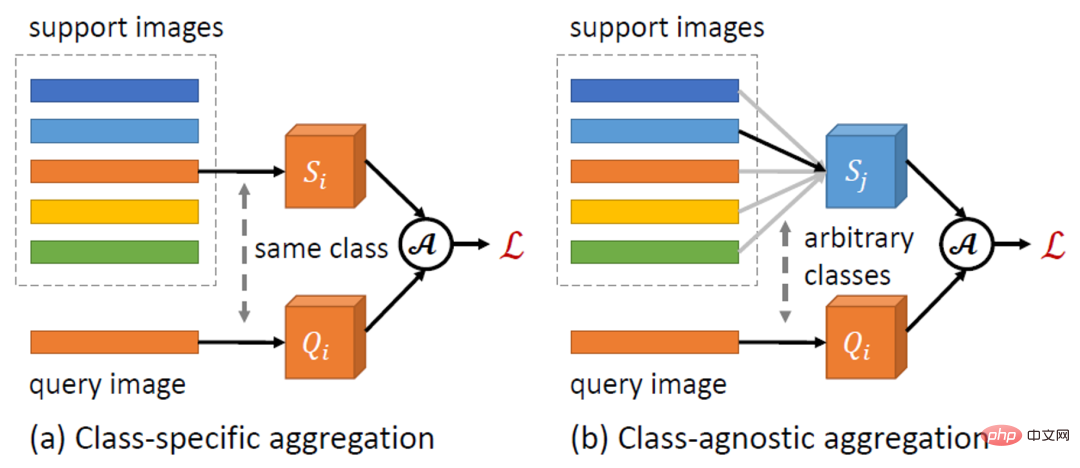
##図 1: カテゴリに依存しない特徴集約 CAAA の概略図
この記事では、シンプルかつ効果的 カテゴリに依存しない特徴集約手法 CAA。上の図 1 に示すように、CAA では異なるクラス間の特徴集約が可能であり、これによりモデルがクラスに依存しない表現を学習することが促進され、クラス間のバイアスやクラス間の混乱が軽減されます。具体的には、カテゴリ の各 RoI 機能 と一連のサポート機能 
 、
、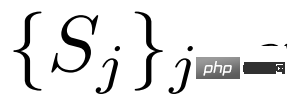 に対して、クラスをランダムに選択します。サポート機能 の
に対して、クラスをランダムに選択します。サポート機能 の  ## は、クエリ機能
## は、クエリ機能 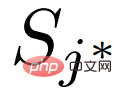
#次に、集約された特徴を
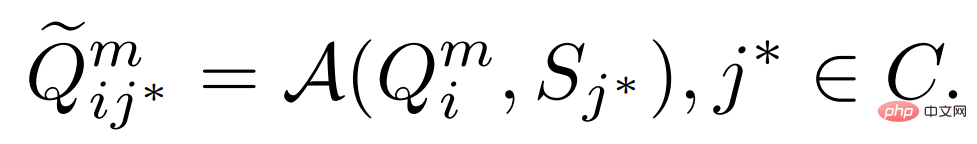

分類スコア

を出力します。
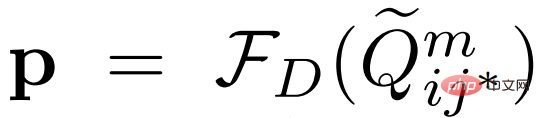 変動特徴集約 VFA
変動特徴集約 VFA
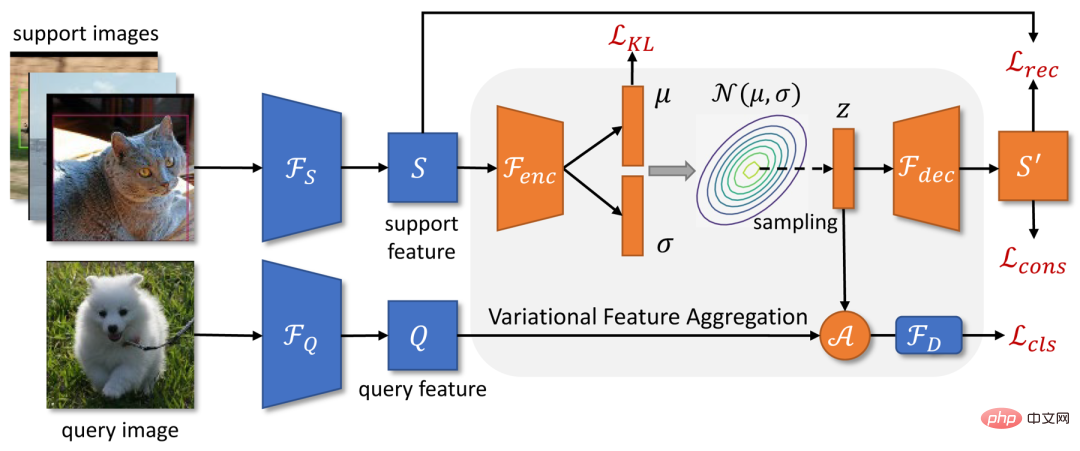
前へwork は通常、カテゴリの中心を表すためにサポート サンプルを単一の特徴ベクトルにエンコードします。ただし、サンプルが小さく分散が大きい場合、クラス中心を正確に推定することが困難になります。このペーパーでは、まずサポート機能をクラスを介したディストリビューションに変換します。推定されたクラス分布は特定のサンプルに偏っていないため、分布からサンプリングされた特徴はサンプルの分散に対して比較的堅牢です。 VFA のフレームワークは上の図 2 に示されています。
#a) 変分特徴学習#。 VFA は、カテゴリの分布を学習するために変分オートエンコーダ VAE [4] を採用しています。図 2 に示すように、サポート特徴 S の場合、最初にエンコーダ を使用して、分布パラメータ  および
および  を推定します。次に、変分推論を通じて分布
を推定します。次に、変分推論を通じて分布  から
から 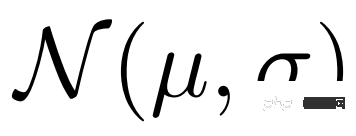 をサンプリングし、最後にデコーダを通じて再構成された値を取得します。
をサンプリングし、最後にデコーダを通じて再構成された値を取得します。  サポート機能
サポート機能 。 VAE を最適化する場合、一般的な KL 損失
。 VAE を最適化する場合、一般的な KL 損失 と再構築損失
と再構築損失 に加えて、この記事では一貫性損失も使用して、学習された分布にカテゴリ情報を保持させます。 # ########################################
に加えて、この記事では一貫性損失も使用して、学習された分布にカテゴリ情報を保持させます。 # ########################################
b) 変分特徴融合。サポート機能はカテゴリのディストリビューションに変換されるため、ディストリビューションからフィーチャをサンプリングし、クエリ機能を使用してそれらを集約できます。具体的には、VFA もカテゴリに依存しない集約 CAA を使用しますが、クエリ特徴  と変分特徴
と変分特徴  を集約します。クラス
を集約します。クラス  のクエリ機能
のクエリ機能  とクラス
とクラス  のサポート機能
のサポート機能 
を考慮して、最初にその分布 ## を推定します。 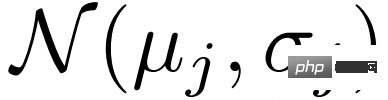 # と変分特徴量
# と変分特徴量 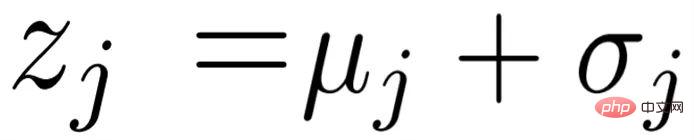 ; を抽出し、次の式でそれらを融合します:
; を抽出し、次の式でそれらを融合します:
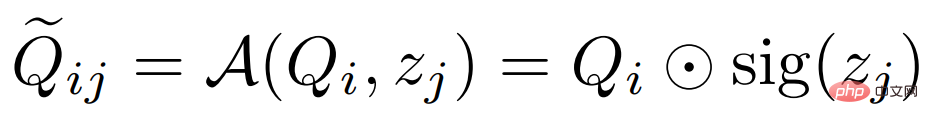
ここで、 はチャネル乗算を表し、sig はシグモイド演算の略です。トレーニング フェーズでは、集計のためにサポート機能 をランダムに選択します。テスト フェーズでは、
はチャネル乗算を表し、sig はシグモイド演算の略です。トレーニング フェーズでは、集計のためにサポート機能 をランダムに選択します。テスト フェーズでは、
のサポート機能  を平均します。クラス値
を平均します。クラス値  、分布
、分布 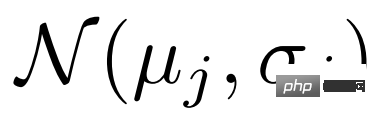 を推定します。ここで、
を推定します。ここで、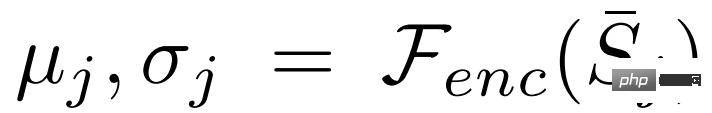 。
。
分類 - 回帰タスクの分離
通常、検出サブネットワーク  には、共有特徴抽出器
には、共有特徴抽出器 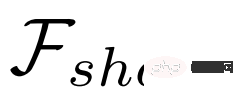 と 2 つの独立したネットワーク (分類サブネットワーク ##) が含まれています。
と 2 つの独立したネットワーク (分類サブネットワーク ##) が含まれています。  # および回帰サブネットワーク
# および回帰サブネットワーク  。以前の研究では、集約された特徴は、オブジェクト分類と境界ボックス回帰のために検出サブネットワークに入力されました。ただし、分類タスクには翻訳不変の特徴が必要ですが、回帰には翻訳共変の特徴が必要です。サポート特徴はカテゴリの中心を表し、変換不変であるため、集約された特徴は回帰タスクに悪影響を及ぼします。
。以前の研究では、集約された特徴は、オブジェクト分類と境界ボックス回帰のために検出サブネットワークに入力されました。ただし、分類タスクには翻訳不変の特徴が必要ですが、回帰には翻訳共変の特徴が必要です。サポート特徴はカテゴリの中心を表し、変換不変であるため、集約された特徴は回帰タスクに悪影響を及ぼします。
この記事では、単純な分類と回帰タスクの分離を提案します。  と
と  が元の集計されたクエリ特徴を表すものとします。前の方法では、両方のタスクに
が元の集計されたクエリ特徴を表すものとします。前の方法では、両方のタスクに  を使用します。ここで、分類スコア
を使用します。ここで、分類スコア  および予測境界ボックス
および予測境界ボックス 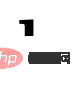 は次のように定義されます:
は次のように定義されます:
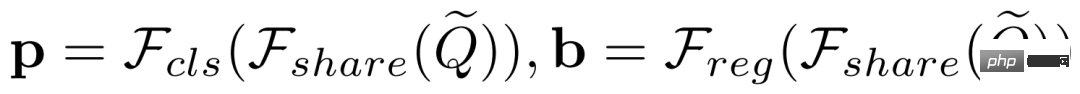
を使用します: 
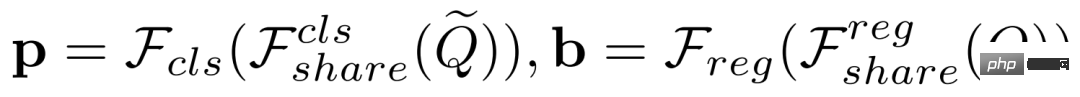
実験評価
PASCAL VOC、MS COCO。 評価指標: 新規クラス平均精度 nAP、基本クラス平均精度 bAP。
主な結果
VFA は両方のデータセットで良好な結果を達成しました。たとえば、PASCAL VOC データセット (以下の表 2) では、VFA は以前の方法よりも大幅に高く、VFA の 1 ショットの結果は、一部の方法の 10 ショットの結果よりもさらに高くなっています。
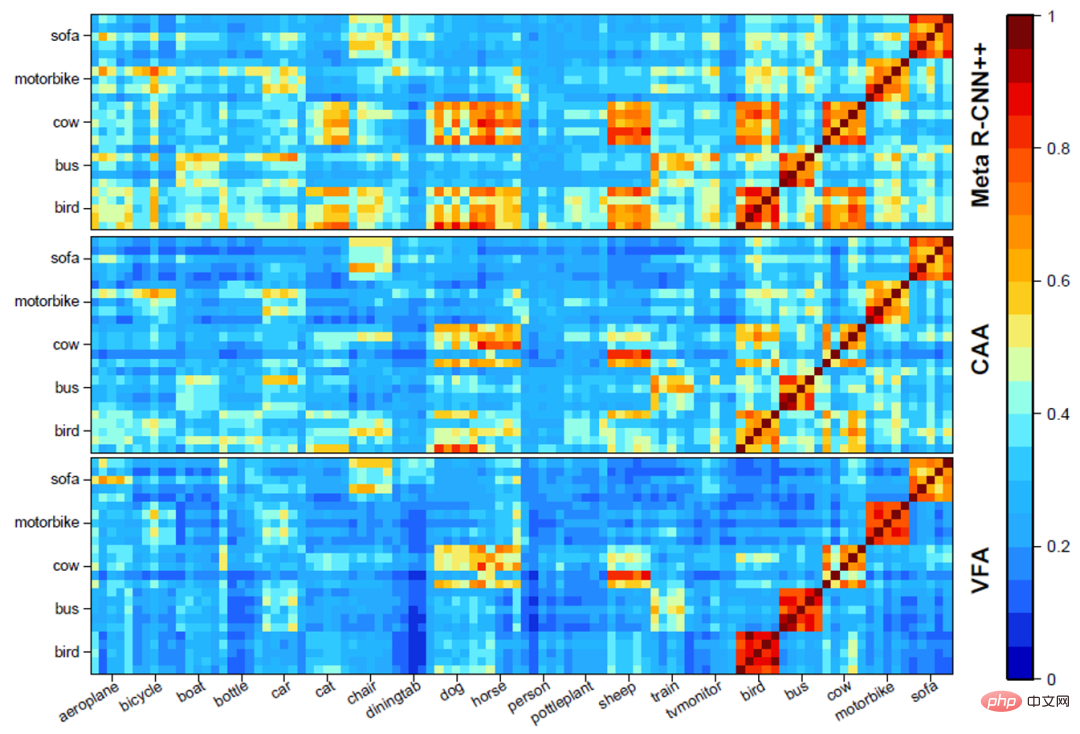
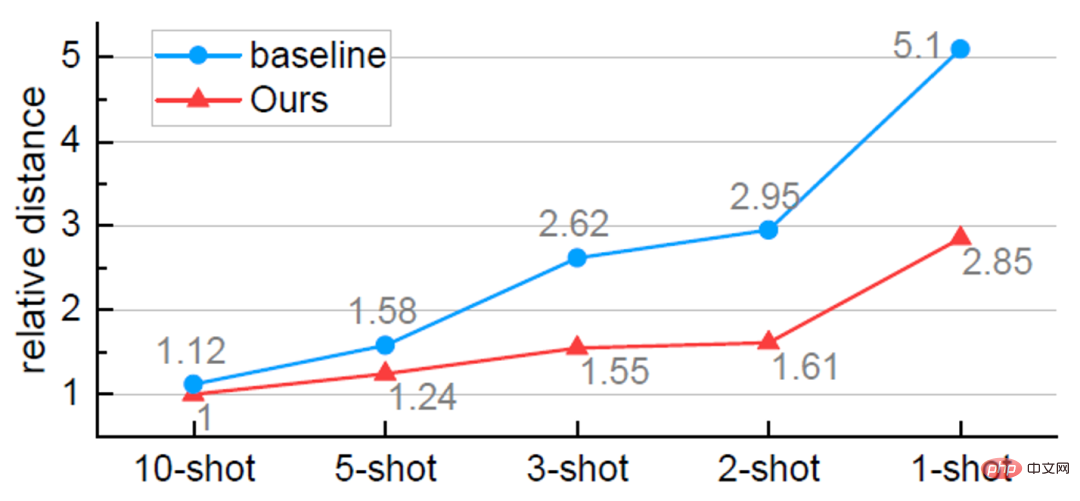
アブレーション実験 a) さまざまなモジュールの役割 。以下の表 3 に示すように、VFA のさまざまなモジュールが連携してモデルのパフォーマンスを向上させることができます。 b) さまざまな特徴集約方法の視覚的分析。以下の図 3 に示すように、CAA は基本クラスと新しいクラスの間の混乱を減らすことができ、VFA は CAA に基づいてクラス間の区別をさらに強化します。 ##c) より正確なカテゴリ中心点の推定。以下の図 4 に示すように、VFA はカテゴリの中心をより正確に推定できます。そして、サンプル数が減少するにつれて、推定の精度はベースライン手法よりも徐々に高くなります。これは、サンプル数が少ない (K=1) ときにこの方法のパフォーマンスが向上する理由も説明します。 d) 結果の視覚化##。 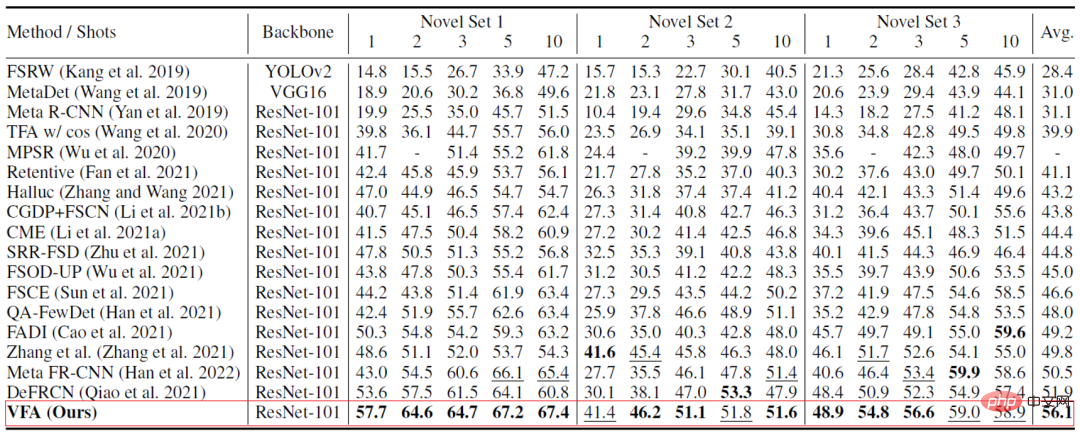
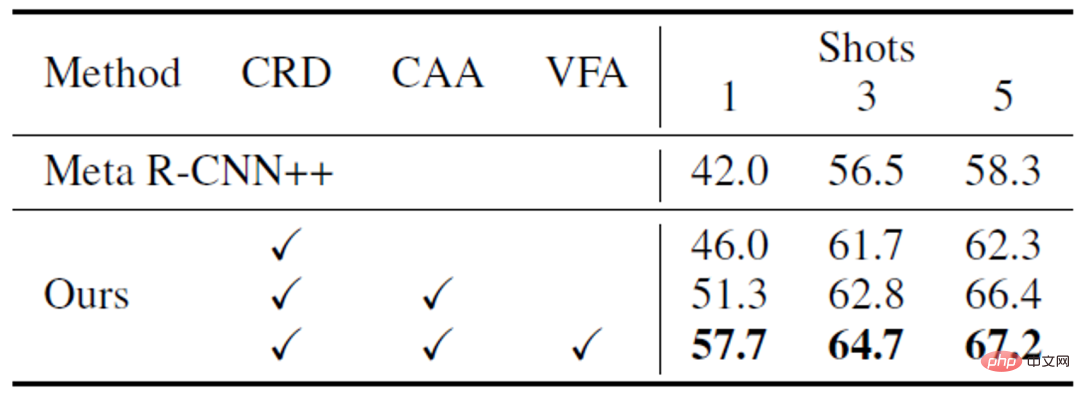

本稿では、FSODにおけるメタ学習に基づく特徴集約手法に立ち戻り、カテゴリ非依存の特徴集約CAAと変分特徴集約VFAを提案する。 CAA は、基本クラスと新規クラスの間のクラスのバイアスと混乱を軽減できます。VFA は、サンプルをクラス分布に変換して、より堅牢な特徴の集約を実現します。 PASCAL VOC および MS COCO データセットの実験は、この論文で提案された方法の有効性を示しています。
以上が新しい SOTA を実現するための、変分特徴集約に基づく回帰メタ学習、少数サンプルのターゲット検出の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

Video Face Swap
完全無料の AI 顔交換ツールを使用して、あらゆるビデオの顔を簡単に交換できます。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7675
7675
 15
15
 1393
1393
 52
52
 1207
1207
 24
24
 91
91
 11
11
 i7-7700 が Windows 11 にアップグレードできない場合の解決策
Dec 26, 2023 pm 06:52 PM
i7-7700 が Windows 11 にアップグレードできない場合の解決策
Dec 26, 2023 pm 06:52 PM
i77700 のパフォーマンスは win11 を実行するのに完全に十分ですが、ユーザーは i77700 を win11 にアップグレードできないことがわかります。これは主に Microsoft によって課された制限が原因であるため、この制限をスキップする限りインストールできます。 i77700 は win11 にアップグレードできません: 1. Microsoft が CPU バージョンを制限しているためです。 2. win11 に直接アップグレードできるのは、Intel の第 8 世代以降のバージョンのみです 3. i77700 は第 7 世代として、win11 のアップグレードのニーズを満たすことができません。 4. ただし、i77700はパフォーマンス的にはwin11を快適に使用するのに完全に可能です。 5. したがって、このサイトの win11 直接インストール システムを使用できます。 6. ダウンロードが完了したら、ファイルを右クリックして「ロード」します。 7. ダブルクリックして「ワンクリック」を実行します。
 転倒検知、骨格点人間動作認識に基づき、コードの一部はChatgptで完成
Apr 12, 2023 am 08:19 AM
転倒検知、骨格点人間動作認識に基づき、コードの一部はChatgptで完成
Apr 12, 2023 am 08:19 AM
こんにちは、みんな。今日は転倒検知プロジェクトについてお話ししたいと思います。正確に言うと、骨格点に基づく人間の動作認識です。大きく3つのステップに分かれています:人体認識、人体骨格点動作分類プロジェクトのソースコードがパッケージ化されています。入手方法については記事の最後を参照してください。 0. chatgpt まず、監視対象のビデオ ストリームを取得する必要があります。このコードは比較的固定されており、chatgpt で記述したコードを直接 chatgpt に完成させることができますが、問題なくそのまま使用できます。しかし、後のビジネス タスク (メディアパイプを使用して人間のスケルトン ポイントを特定するなど) になると、chatgpt によって指定されたコードは正しくありません。 chatgpt はビジネスロジックから独立したツールボックスとして使用できると思います。
 MIT の最新傑作: GPT-3.5 を使用して時系列異常検出の問題を解決する
Jun 08, 2024 pm 06:09 PM
MIT の最新傑作: GPT-3.5 を使用して時系列異常検出の問題を解決する
Jun 08, 2024 pm 06:09 PM
今日は、MIT が先週公開した記事を紹介します。GPT-3.5-turbo を使用して時系列異常検出の問題を解決し、時系列異常検出における LLM の有効性を最初に検証しました。プロセス全体に微調整はなく、GPT-3.5-turbo は異常検出に直接使用されます。この記事の核心は、時系列を GPT-3.5-turbo が認識できる入力に変換する方法とその設計方法です。 LLM が異常検出タスクを解決できるようにするためのプロンプトまたはパイプライン。この作品について詳しく紹介していきます。画像用紙タイトル:Large languagemodelscanbeゼロショタノマリデテ
 改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
改良された検出アルゴリズム: 高解像度の光学式リモートセンシング画像でのターゲット検出用
Jun 06, 2024 pm 12:33 PM
01 今後の概要 現時点では、検出効率と検出結果の適切なバランスを実現することが困難です。我々は、光学リモートセンシング画像におけるターゲット検出ネットワークの効果を向上させるために、多層特徴ピラミッド、マルチ検出ヘッド戦略、およびハイブリッドアテンションモジュールを使用して、高解像度光学リモートセンシング画像におけるターゲット検出のための強化されたYOLOv5アルゴリズムを開発しました。 SIMD データセットによると、新しいアルゴリズムの mAP は YOLOv5 より 2.2%、YOLOX より 8.48% 優れており、検出結果と速度のバランスがより優れています。 02 背景と動機 リモート センシング技術の急速な発展に伴い、航空機、自動車、建物など、地表上の多くの物体を記述するために高解像度の光学式リモート センシング画像が使用されています。リモートセンシング画像の判読における物体検出
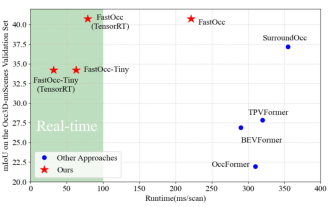 SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
SOTA をリアルタイムで追加すると、大幅に増加します。 FastOcc: より高速な推論と展開に適した Occ アルゴリズムが登場しました。
Mar 14, 2024 pm 11:50 PM
上記と著者の個人的な理解は、自動運転システムにおいて、認識タスクは自動運転システム全体の重要な要素であるということです。認識タスクの主な目的は、自動運転車が道路を走行する車両、路側の歩行者、運転中に遭遇する障害物、道路上の交通標識などの周囲の環境要素を理解して認識できるようにすることで、それによって下流のシステムを支援できるようにすることです。モジュール 正しく合理的な決定と行動を行います。自動運転機能を備えた車両には、通常、サラウンドビューカメラセンサー、ライダーセンサー、ミリ波レーダーセンサーなど、さまざまな種類の情報収集センサーが装備されており、自動運転車が正確に認識し、認識できるようにします。周囲の環境要素を理解することで、自動運転車が自動運転中に正しい判断を下せるようになります。頭
 PHP 言語開発で null 値エラーを検出して処理するにはどうすればよいですか?
Jun 11, 2023 am 10:51 AM
PHP 言語開発で null 値エラーを検出して処理するにはどうすればよいですか?
Jun 11, 2023 am 10:51 AM
最新の Web アプリケーションの継続的な開発により、PHP は最も人気のあるプログラミング言語の 1 つとして、Web サイト開発で広く使用されています。ただし、開発プロセス中に NULL 値エラーが頻繁に発生し、これらのエラーによりアプリケーションが例外をスローし、ユーザー エクスペリエンスに影響を与える可能性があります。したがって、PHP 開発プロセスにおいて、Null エラーを検出して対処する方法は、プログラマーが習得する必要がある重要なスキルです。 1. NULL 値エラーとは何ですか? PHP 開発プロセスでは、NULL 値エラーは通常、初期化されていない変数と可変変数という 2 つの状況を指します。
 AAAI2024: Far3D - 150m まで直接到達する視覚的な 3D ターゲット検出の革新的なアイデア
Dec 15, 2023 pm 01:54 PM
AAAI2024: Far3D - 150m まで直接到達する視覚的な 3D ターゲット検出の革新的なアイデア
Dec 15, 2023 pm 01:54 PM
最近、Arxiv で純粋視覚周囲知覚に関する最新の研究を読みました。この研究は PETR シリーズの手法に基づいており、長距離ターゲット検出の純粋視覚問題の解決に焦点を当てており、知覚範囲を 150 メートルに拡張しています。この論文の手法と結果は非常に参考になるので、解釈してみました 原題:Far3D: Expanding the Horizon for Surround-view3DObject Detection 論文リンク: https://arxiv.org/abs/2308.09616 :北京工業大学 & Megvii Technology タスクの背景 自動運転の理解における 3D 物体検出
 変圧器を使用して、ライダー、ミリ波レーダー、視覚的特徴を効果的に関連付けるにはどうすればよいですか?
Apr 19, 2024 pm 04:01 PM
変圧器を使用して、ライダー、ミリ波レーダー、視覚的特徴を効果的に関連付けるにはどうすればよいですか?
Apr 19, 2024 pm 04:01 PM
著者が自動運転を個人的に理解するための基本的なタスクの 1 つは 3 次元のターゲット検出であり、現在では多くの方法がマルチセンサー フュージョンに基づいて実装されています。では、なぜマルチセンサーフュージョンが必要なのでしょうか? それがライダーとカメラのフュージョンであっても、ミリ波レーダーとカメラのフュージョンであっても、主な目的は、点群と画像の間の補完的な接続を使用して、ターゲット検出の精度を向上させることです。コンピューター ビジョンの分野で Transformer アーキテクチャを継続的に適用することで、アテンション メカニズムに基づく手法により、複数のセンサー間の融合の精度が向上しました。共有された 2 つの論文は、このアーキテクチャに基づいており、それぞれのモダリティの有用な情報をさらに活用し、より優れた融合を達成するための新しい融合方法を提案しています。 TransFusion: 主な貢献




