 テクノロジー周辺機器
テクノロジー周辺機器
 AI
AI
 GPT-3 の数学問題を解く精度は 92.5% に向上しました。 Microsoft、微調整せずに「科学」言語モデルを作成する MathPrompter を提案
GPT-3 の数学問題を解く精度は 92.5% に向上しました。 Microsoft、微調整せずに「科学」言語モデルを作成する MathPrompter を提案
GPT-3 の数学問題を解く精度は 92.5% に向上しました。 Microsoft、微調整せずに「科学」言語モデルを作成する MathPrompter を提案
大規模な言語モデルの最も批判されている欠点は、深刻なナンセンスを除けば、おそらく「数学ができない」ことでしょう。
たとえば、複数ステップの推論を必要とする複雑な数学的問題の場合、言語モデルは通常、正しい答えを与えることができません。 「思考の連鎖」技術のおかげで、途中の段階でエラーが発生することがよくあります。
文系の自然言語理解課題とは異なり、数学の問題は正解が 1 つしかなく、答えの範囲もそれほど広くないため、正確な解を導き出すことが困難です。大規模な言語モデルの場合は、より困難だと言えます。
さらに、数学的な問題に関しては、既存の言語モデルでは通常、答えに対する信頼性が提供されず、ユーザーは生成された答えの信頼性を判断できなくなります。
この問題を解決するために、Microsoft Research は、予測への依存度を高めながら、算術問題における LLM のパフォーマンスを向上させることができる MathPrompter テクノロジを提案しました。
論文リンク: https://arxiv.org/abs/2303.05398
MathPrompter はゼロショット思考を使用しますチェーン ヒンティング テクノロジは、複数の代数式または Python 関数を生成して、同じ数学的問題をさまざまな方法で解決することで、出力結果の信頼性を高めます。
他のヒントベースの CoT メソッドと比較して、MathPrompter は中間ステップの妥当性もチェックします。
175B パラメーター GPT に基づいて、MathPrompter メソッドを使用して MultiArith データ セットの精度を 78.7% から 92.5% に向上させました。
数学に特化したプロンプト
近年の自然言語処理の発展は、大規模言語モデル (LLM) の規模が拡大し続けていることによるところが大きいです。は、驚くべきゼロショットおよび少数ショット機能を実証し、プロンプト技術の開発にも貢献しました。ユーザーは、プロンプトでいくつかの簡単な例を LLM に入力するだけで、新しいタスクを予測できます。
プロンプトは、単一ステップのタスクでは非常に成功していると言えますが、複数ステップの推論が必要なタスクでは、プロンプト技術のパフォーマンスはまだ不十分です。
人間は複雑な問題を解決するとき、それを分解して段階的に解決しようとします。「思考連鎖」(CoT) 促進テクノロジーは、この直感を LLM に拡張します。推論を必要とするさまざまな NLP タスクにわたってパフォーマンスの向上が達成されました。
この論文では、主に「数学的推論タスクを解決するため」の Zero-shot-CoT メソッドを研究しています。以前の研究では、MultiArith データセットの精度が大幅に向上しました。17.7% から向上しました。
#1. モデルが従う思考の連鎖は結果を改善しますが、思考の連鎖をチェックするわけではありません。続く各ステップの結果;
2. LLM 予測結果には信頼性がありません。
MathPrompterこれらのギャップをある程度解決するために、研究者は「人間が数学の問題を解決する方法」からインスピレーションを得て、複雑な問題をより単純な複数ステップの手順に分解しました。 、複数のメソッドを利用して各ステップでメソッドを検証します。
#LLM は生成モデルであるため、特に数学的推論タスクの場合、生成された答えが正確であることを確認するのは非常に困難になります。
研究者は、生徒が算数の問題を解くプロセスを観察し、生徒が解決策を検証するために行ったいくつかの手順を要約しました:
既知の結果との準拠 ソリューションを既知の結果と比較することで、その精度を評価し、必要な調整を行うことができます。これは、問題が以下のような標準的な問題の場合に特に役立ちます。成熟したソリューション。
マルチ検証は、複数の角度から問題にアプローチし、結果を比較することで、ソリューションの有効性を確認し、ソリューションが合理的かつ正確であることを保証します。 。
クロスチェック、問題を解決するプロセスは、最終的な答えと同じくらい必要です。プロセスの中間ステップが正しいことを検証することで、明確な答えを得ることができます。ソリューションの理解、その背後にある思考プロセス。
#計算検証: 電卓またはコンピューターを使用して算術計算を実行すると、最終的な答えの精度を検証できます
具体的に質問すると、

## レストランでの大人の食事の料金は次のとおりです。 5ドル、子供は無料で食べられます。 15 人が来て、そのうち 8 人が子供である場合、このグループの食事の費用はいくらですか?
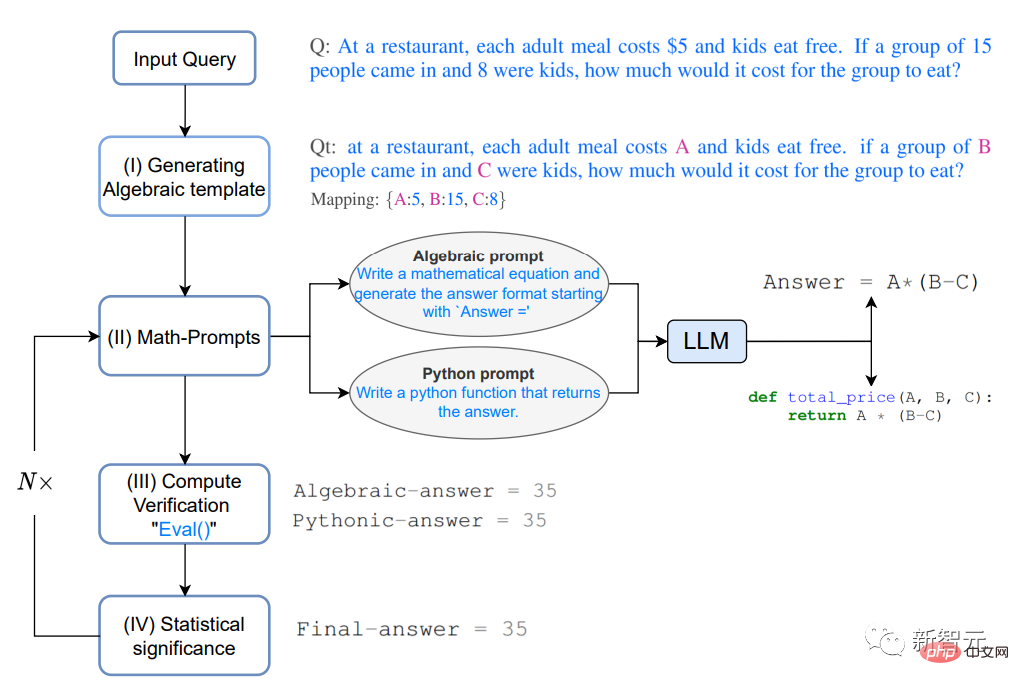
#1. 代数テンプレートの生成#まず問題を解決します 代数に変換しますこの形式では、キーと値のマップを使用して数値項を変数に置き換えることで、修正された質問 Qt

複数の検証とクロスチェックの上記の思考プロセスによって得られた直感に基づいて、2 つの異なる方法を使用して Qt 分析ソリューションを生成しますは、代数的および Python の両方で、Qt の追加コンテキストを生成するための次のヒントを LLM に提供します。
#プロンプトは、「代数式を導出する」または「Python 関数を作成する」です。

LLM モデルは、プロンプトに応答した後、次の式を出力できます。
上記で生成された分析計画は、LLM の「中間思考プロセス」に関するヒントをユーザーに提供します。ヒントを追加すると、結果の精度が向上します。 . 精度と一貫性が向上し、より正確で効率的なソリューションを生成する MathPrompter の能力が向上します。

#3. 計算の検証
Qt で複数の入力変数を使用するランダム キー - value マップを使用して、前のステップで生成された式を評価します。Python の eval() メソッドを使用してこれらの式を評価します。
次に、出力結果を比較して、答えに一致した意見が見つかるかどうかを確認します。これにより、答えが正しく、信頼できるというより高い信頼度も得られます。
式が出力に一致すると、入力 Q の変数値を使用して最終的な計算が行われます。答え。

4. 統計的有意性
さまざまな式の出力でのコンセンサスを確保するには、ステップ 2 と 3 をほぼ繰り返します。実験を 5 回行い、最も頻繁に観察された回答値を報告します。
明確な合意がない場合は、ステップ 2、3、4 を繰り返します。
実験結果
MathPrompter は MultiArith データ セットで評価されました。その中の数学的質問は、複雑な算術演算を実行する機械学習モデルの能力をテストするために特に使用され、適切に解決するには、さまざまな算術演算と論理的推論を適用する必要があります。
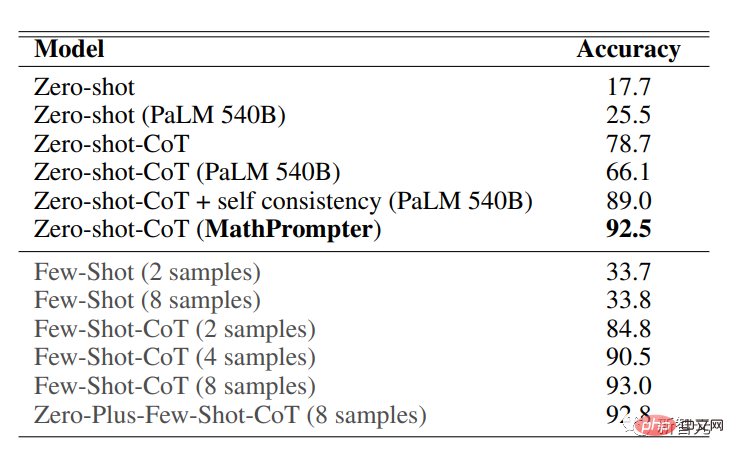
MultiArith データセットの精度結果は、MathPrompter がすべての Zero-shot および Zero -shot- よりも優れたパフォーマンスを示していることを示しています。 CoT ベースライン、精度が 78.7% から 92.5% に向上
175B パラメーター GPT3 DaVinci に基づく MathPrompter モデルのパフォーマンスが 540B パラメーター モデルのパフォーマンスに匹敵することがわかります。 SOTA の Few -shot-CoT メソッドと同等です。

上記の表からわかるように、MathPrompter の設計により、「生成された答えには 1 段階の違いがある場合があります。」という問題は、モデルを複数回実行し、コンセンサス結果を報告することで回避できます。
さらに、推論ステップが長すぎる可能性があるという問題は、通常必要なトークンが少ない Python または代数手法で解決できます。 #また、推論ステップは正しくても、最終的な計算結果が正しくない場合がありますが、MathPrompter では Python の eval() メソッド関数を使用してこの問題を解決します。
ほとんどの場合、MathPrompter は正しい中間解答と最終解答を生成できますが、表の最後の質問のように、代数出力と Python 出力が一致する場合もいくつかあります。はい、しかしエラーがあります。
以上がGPT-3 の数学問題を解く精度は 92.5% に向上しました。 Microsoft、微調整せずに「科学」言語モデルを作成する MathPrompter を提案の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7518
7518
 15
15
 1378
1378
 52
52
 81
81
 11
11
 21
21
 67
67
 ChatGPT では、無料ユーザーが 1 日あたりの制限付きで DALL-E 3 を使用して画像を生成できるようになりました
Aug 09, 2024 pm 09:37 PM
ChatGPT では、無料ユーザーが 1 日あたりの制限付きで DALL-E 3 を使用して画像を生成できるようになりました
Aug 09, 2024 pm 09:37 PM
DALL-E 3は、前モデルより大幅に改良されたモデルとして2023年9月に正式導入されました。これは、複雑な詳細を含む画像を作成できる、これまでで最高の AI 画像ジェネレーターの 1 つと考えられています。ただし、発売当初は対象外でした
 AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI が数学研究を破壊する!フィールズ賞受賞者で中国系アメリカ人の数学者が上位 11 件の論文を主導 | テレンス・タオが「いいね!」しました
Apr 09, 2024 am 11:52 AM
AI は確かに数学を変えつつあります。最近、この問題に細心の注意を払っている陶哲軒氏が『米国数学協会会報』(米国数学協会会報)の最新号を送ってくれた。 「機械は数学を変えるのか?」というテーマを中心に、多くの数学者が意見を述べ、そのプロセス全体は火花に満ち、ハードコアで刺激的でした。著者には、フィールズ賞受賞者のアクシャイ・ベンカテシュ氏、中国の数学者鄭楽軍氏、ニューヨーク大学のコンピューター科学者アーネスト・デイビス氏、その他業界で著名な学者を含む強力な顔ぶれが揃っている。 AI の世界は劇的に変化しています。これらの記事の多くは 1 年前に投稿されたものです。
 ChatGPT と Python の完璧な組み合わせ: インテリジェントな顧客サービス チャットボットの作成
Oct 27, 2023 pm 06:00 PM
ChatGPT と Python の完璧な組み合わせ: インテリジェントな顧客サービス チャットボットの作成
Oct 27, 2023 pm 06:00 PM
ChatGPT と Python の完璧な組み合わせ: インテリジェント カスタマー サービス チャットボットの作成 はじめに: 今日の情報化時代において、インテリジェント カスタマー サービス システムは企業と顧客の間の重要なコミュニケーション ツールとなっています。より良い顧客サービス体験を提供するために、多くの企業が顧客相談や質問応答などのタスクを完了するためにチャットボットに注目し始めています。この記事では、OpenAI の強力なモデル ChatGPT と Python 言語を使用して、インテリジェントな顧客サービス チャットボットを作成し、顧客サービスを向上させる方法を紹介します。
 携帯電話にchatgptをインストールする方法
Mar 05, 2024 pm 02:31 PM
携帯電話にchatgptをインストールする方法
Mar 05, 2024 pm 02:31 PM
インストール手順: 1. ChatGTP ソフトウェアを ChatGTP 公式 Web サイトまたはモバイル ストアからダウンロードします; 2. それを開いた後、設定インターフェイスで言語を中国語を選択します; 3. ゲーム インターフェイスでヒューマン マシン ゲームを選択し、中国スペクトル; 4 . 起動後、チャット ウィンドウにコマンドを入力してソフトウェアを操作します。
 ChatGPT と Java を使用してインテリジェントなチャットボットを開発する方法
Oct 28, 2023 am 08:54 AM
ChatGPT と Java を使用してインテリジェントなチャットボットを開発する方法
Oct 28, 2023 am 08:54 AM
この記事では、ChatGPT と Java を使用してインテリジェントなチャットボットを開発する方法を紹介し、いくつかの具体的なコード例を示します。 ChatGPT は、OpenAI によって開発された生成事前トレーニング トランスフォーマーの最新バージョンです。これは、自然言語を理解し、人間のようなテキストを生成できるニューラル ネットワーク ベースの人工知能テクノロジーです。 ChatGPT を使用すると、適応型チャットを簡単に作成できます
 中国でもchatgptは使えますか?
Mar 05, 2024 pm 03:05 PM
中国でもchatgptは使えますか?
Mar 05, 2024 pm 03:05 PM
chatgpt は中国でも使用できますが、香港やマカオでも登録できません。ユーザーが登録したい場合は、外国の携帯電話番号を使用して登録できます。登録プロセス中にネットワーク環境を切り替える必要があることに注意してください。外国のIP。
 ChatGPTとPythonを使ってユーザー意図認識機能を実装する方法
Oct 27, 2023 am 09:04 AM
ChatGPTとPythonを使ってユーザー意図認識機能を実装する方法
Oct 27, 2023 am 09:04 AM
ChatGPT と Python を使用してユーザー意図認識機能を実装する方法 はじめに: 今日のデジタル時代において、人工知能技術はさまざまな分野で徐々に不可欠な部分になりました。その中で、自然言語処理 (Natural Language Processing、NLP) テクノロジーの開発により、機械が人間の言語を理解して処理できるようになります。 ChatGPT (Chat-GeneratingPretrainedTransformer) は、
 ChatGPT PHP を使用してインテリジェントな顧客サービス ロボットを構築する方法
Oct 28, 2023 am 09:34 AM
ChatGPT PHP を使用してインテリジェントな顧客サービス ロボットを構築する方法
Oct 28, 2023 am 09:34 AM
ChatGPTPHP を使用してインテリジェントな顧客サービス ロボットを構築する方法 はじめに: 人工知能技術の発展に伴い、顧客サービスの分野でロボットの使用が増えています。 ChatGPTPHP を使用してインテリジェントな顧客サービス ロボットを構築すると、企業はより効率的でパーソナライズされた顧客サービスを提供できるようになります。この記事では、ChatGPTPHP を使用してインテリジェントな顧客サービス ロボットを構築する方法を紹介し、具体的なコード例を示します。 1. ChatGPTPHP をインストールし、ChatGPTPHP を使用してインテリジェントな顧客サービス ロボットを構築します。



