デシジョン ツリー アルゴリズムの構造
翻訳者| Zhao Qingyu
査読者| Sun Shujuan
序文
機械学習では、分類には 2 つの段階があります。それぞれ学習段階と予測段階です。学習フェーズでは、指定されたトレーニング データに基づいてモデルが構築され、予測フェーズでは、そのモデルはデータに基づいて応答を予測するために使用されます。デシジョン ツリーは、理解して説明するのが最も簡単な分類アルゴリズムの 1 つです。
機械学習では、分類には学習段階と予測段階の 2 つの段階があります。学習フェーズでは、指定されたトレーニング データに基づいてモデルが構築され、予測フェーズでは、そのモデルはデータに基づいて応答を予測するために使用されます。デシジョン ツリーは、理解して説明するのが最も簡単な分類アルゴリズムの 1 つです。
デシジョン ツリー アルゴリズム
デシジョン ツリー アルゴリズムは、教師あり学習アルゴリズムの 1 つです。他の教師あり学習アルゴリズムとは異なり、デシジョン ツリー アルゴリズムは回帰問題と分類問題の両方を解決するために使用できます。
デシジョン ツリーを使用する目的は、以前のデータ (トレーニング データ) から推測される単純な決定ルールを学習することによって、ターゲット変数のクラスまたは値を予測するトレーニング モデルを作成することです。
デシジョン ツリーでは、ツリーのルートから開始してレコードのクラス ラベルを予測します。ルート属性の値を記録された属性と比較し、その比較に基づいて、この値に対応する分岐をたどって次のノードにジャンプします。
デシジョン ツリーの種類
ターゲット変数の種類に基づいて、ツリーを 2 つのタイプに分けることができます:
1. カテゴリ変数デシジョン ツリー: はい デシジョンカテゴリカルターゲット変数のツリーは、カテゴリカル変数決定木と呼ばれます。
2. 連続変数決定木: 決定木の対象変数が連続であるため、連続変数決定木と呼ばれます。
例: 顧客が保険会社に更新料を支払うかどうかを予測するという問題があるとします。ここでは顧客の収入が重要な変数ですが、保険会社はすべての顧客の収入の詳細を把握しているわけではありません。これが重要な変数であることがわかったので、職業、製品、その他のさまざまな変数に基づいて顧客の収益を予測するデシジョン ツリーを構築できます。この場合、ターゲット変数は連続であると予測します。
デシジョン ツリーに関する重要な用語
1. ルート ノード (ルート ノード): メンバーまたはサンプル全体を表し、さらに 2 つ以上の同じタイプのコレクションに分割されます。
2. 分割): ノードを 2 つ以上の子ノードに分割するプロセス。
3. 意思決定ノード: 子ノードがさらに多くの子ノードに分割される場合、その子ノードは意思決定ノードと呼ばれます。
4. リーフ/ターミナル ノード: 分割できないノードは、リーフ ノードまたはターミナル ノードと呼ばれます。
5. プルーニング: デシジョン ノードの子ノードを削除するプロセスは、プルーニングと呼ばれます。建設は、分離の逆のプロセスとみなすこともできます。
6. ブランチ/サブツリー: ツリー全体のサブパートはブランチまたはサブツリーと呼ばれます。
7. 親ノードと子ノード: 子ノードに分割できるノードは親ノードと呼ばれ、子ノードは親ノードの子ノードです。
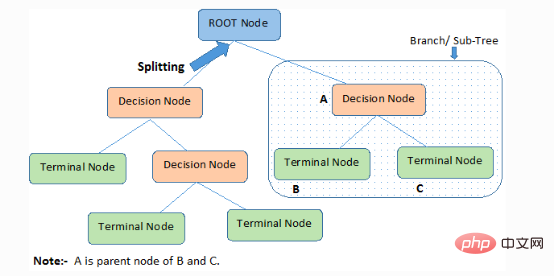
デシジョン ツリーは、ルートからリーフ/終端ノードまでの降順でサンプルを分類し、サンプルの分類方法を提供します。ツリー内の各ノードは特定の属性のテスト ケースとして機能し、ノードからの各下降方向はテスト ケースに対する考えられる答えに対応します。このプロセスは本質的に再帰的であり、新しいノードをルートとする各サブツリーに対して同じように扱われます。
デシジョン ツリーを作成するときに行う仮定
デシジョン ツリーを使用するときに行ういくつかの仮定を次に示します:
#●まず、トレーニング セット全体をルートとして取得します。##●特徴量は分類できればベストです。これらの値が連続値である場合、モデルを構築する前に離散化できます。
#●レコードは属性値に基づいて再帰的に分散されます。 #いくつかの統計的手法を使用して、対応する属性がツリーのルート ノードまたはツリーの内部ノードに順番に配置されます。 デシジョン ツリーは、積の和の式形式に従います。 Sum of Products (SOP) は選言正規形としても知られています。クラスの場合、ツリーのルートから同じクラスのリーフ ノードまでの各分岐は値の結合であり、クラスで終わる異なる分岐は論理和を構成します。 デシジョン ツリーの実装プロセスにおける主な課題は、ルート ノードと各レベル ノードの属性を決定することであり、この問題は属性選択問題です。現在、各レベルでノードの属性を選択するためのさまざまな属性選択方法があります。 デシジョン ツリーはどのように機能しますか?意思決定の分離特性はツリーの精度に重大な影響を与えます。分類ツリーと回帰ツリーの意思決定基準は異なります。 デシジョン ツリーは、さまざまなアルゴリズムを使用して、ノードを 2 つ以上の子ノードに分割することを決定します。子ノードを作成すると、子ノードの均一性が高まります。言い換えれば、ノードの純度はターゲット変数と比較して増加します。デシジョン ツリーは、使用可能なすべての変数でノードを分離し、分割する多くの同型子ノードを生成できるノードを選択します。アルゴリズムはターゲット変数のタイプに基づいて選択されます。次に、デシジョン ツリーで使用されるいくつかのアルゴリズムを見てみましょう:
ID3→(D3 の拡張)
C4.5→(ID3 の後継)
CART→ (分類と回帰木)
CHAID→(カイ二乗自動交互作用検出は分類木計算時に多段階分離を実行)
MARS→(多重適応回帰スプライン)
ID3 アルゴリズムは、トップダウンの貪欲な検索手法を使用して、バックトラックすることなく、可能な分岐空間を通じてデシジョン ツリーを構築します。貪欲なアルゴリズムは、その名前が示すように、常にある時点で最善と思われるものを選択します。
ID3 アルゴリズム ステップ:
1. 元のセット S をルート ノードとして使用します。
2. アルゴリズムの各反復中に、セット S 内の未使用の属性を反復処理し、属性のエントロピー (H) と情報ゲイン (IG) を計算します。
3. 次に、最小のエントロピーまたは最大の情報利得を持つ属性を選択します。
4. 次に、選択した属性を使用してセット S を分離し、データのサブセットを生成します。
5. アルゴリズムは、各反復で以前に選択されたことのない属性のみを考慮して、各サブセットを反復し続けます。
属性選択方法
データ セットに N 個の属性が含まれている場合、どの属性をルート ノードに配置するか、内部ノードとしてツリーのさまざまなレベルに配置するかを決定するのは複雑な手順です。この問題は、任意のノードをルート ノードとしてランダムに選択することによっては解決できません。無作為なアプローチを採用すると、さらに悪い結果が生じる可能性があります。
この属性選択の問題を解決するために、研究者はいくつかのソリューションを設計しました。彼らは、次の基準を使用することを提案しました:
- エントロピー
- 情報利得
- ジニ指数
- 利得率
- 分散削減
- カイ 2 乗
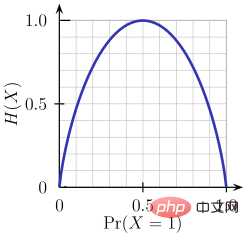

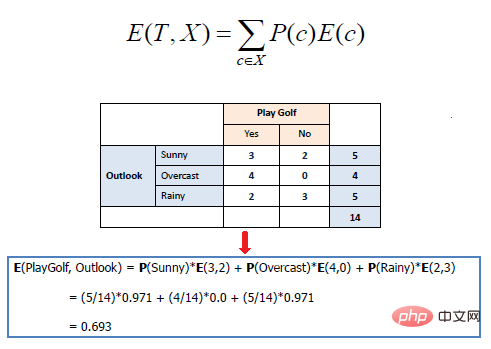
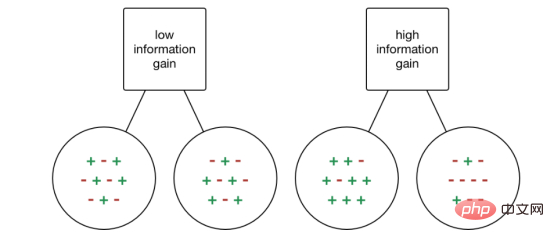

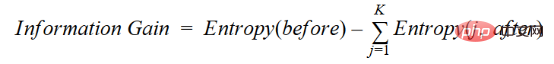
異なる値を持つより小さなパーティションの場合に有利です。
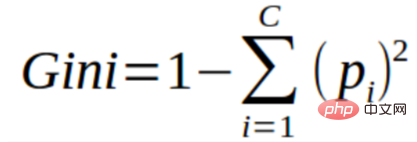
Gini インデックスは、カテゴリカルなターゲット変数「成功」または「失敗」から切り離すことができません。バイナリ分離のみを実行します。ジニ係数が高いほど不平等の程度が大きくなり、不均一性が強くなります。
ジニ指数分離を計算する手順は次のとおりです。
- 次のコマンドを使用して、子ノードのジニ係数を計算します。上記の成功 (p) と失敗 (q) の式は (p² q²) です。
- 分離の各ノードの加重ジニ スコアを使用して、分離のジニ係数インデックスを計算します。
CART (分類および回帰ツリー) は、ジニ指数法を使用して分離点を作成します。
4. 獲得率
情報獲得では、多数の値を持つ属性がルート ノードとして選択される傾向があります。これは、多数の異なる値を持つプロパティが優先されることを意味します。
C4.5 は ID3 の改良された方法で、ゲイン比を使用します。これは情報ゲインを修正してバイアスを低減するもので、通常はこれが最適な方法です。ゲイン レートは、分割を行う前に分岐の数を考慮することで、情報ゲインの問題を解決します。個別の固有情報を考慮に入れることで、情報の獲得を補正します。
ユーザーと、性別、年齢層、階級などの変数に基づいた映画ジャンルの好みを含むデータセットがあるとします。情報獲得の助けを借りて、「性別」で分離します (情報獲得が最も高いと仮定します)。今度は、変数「年齢層」と「評価」も同様に重要になる可能性があります。獲得率の助けを借りて、次のようなプロパティを選択できます。次の層で分離されます。
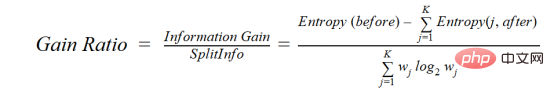
#ここで、before は分離前のデータセット、K は分離によって生成されたサブセットの数、(j, after) は分離後のサブセットです。 j.
5. 分散削減分散削減は、連続ターゲット変数 (回帰問題) に使用されるアルゴリズムです。このアルゴリズムでは、標準分散公式を使用して最適な分離を選択します。母集団を分離する基準として分散が小さい分離を選択します。
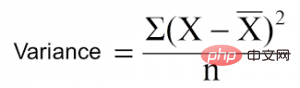
は平均、X は実際の値、n は数値です。価値観の。
分散を計算する手順:
- 各ノードの分散を計算します。
- 各分離の分散を計算し、それを各ノードの分散の加重平均として使用します。
CHAID は、カイ 2 乗自動相互作用検出器の略称です。これは、古いツリー分類方法の 1 つです。子ノードとその親ノードの間の統計的に有意な差を見つけます。ターゲット変数の観測頻度と期待頻度の差の二乗和によって測定します。
これは、カテゴリカル ターゲット変数「成功」または「失敗」で機能します。 2 つ以上の分離を実行できます。カイ二乗値が大きいほど、子ノードと親ノードの差が統計的に有意になります。 CHAID というツリーが生成されます。
数学では、カイ 2 乗は次のように表されます。

カイ 2 乗を計算する手順
- 成功と失敗の偏差を計算して、単一ノードのカイ 2 乗を計算します。
- 別々の値を使用します。各ノードの成功と失敗 すべてのカイ 2 乗の合計により、分離されたカイ 2 乗が計算されます。 ##デシジョン ツリーがあります。特に列がいっぱいのツリーでよくある問題です。場合によっては、ツリーがトレーニング データ セットを記憶しているように見えることがあります。デシジョン ツリーに制約がない場合、最悪の場合、観測ごとに 1 つのリーフが生成されるため、トレーニング データ セットに対して 100% の精度が得られます。したがって、これはトレーニング セットの一部ではないサンプルを予測する際の精度に影響します。
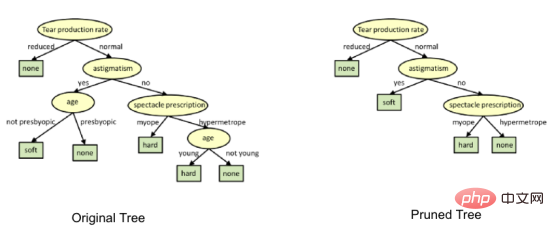
1. デシジョン ツリーの剪定
分離プロセスでは、停止基準に達するまで完全に成長したツリーが生成されます。ただし、成熟したツリーはデータを過剰適合させる可能性があり、その結果、目に見えないデータの精度が低下します。

import numpy as np import matplotlib.pyplot as plt import pandas as pd
その後、次のメソッドを使用してロードします。データセット。ユーザーID、性別、年齢、推定給与、購買状況の5つの属性が含まれます。
data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()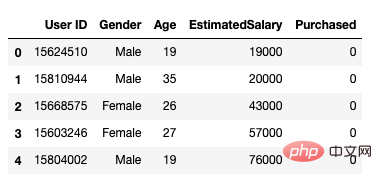
図 1 データセット
年齢と予測のみを組み合わせます。性別やユーザー ID などの他の特性は無関係で、個人の購買力に影響を与えないため、給与が独立変数 X として使用され、y が従属変数となります。
feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values y = data.iloc[:,4].values
次のステップは、データ セットをトレーニング セットとテスト セットに分離することです。
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test =train_test_split(X,y,test_size = 0.25, random_state= 0)
次に特徴スケーリングを実行します
#feature scaling from sklearn.preprocessing import StandardScaler sc_X = StandardScaler() X_train = sc_X.fit_transform(X_train) X_test = sc_X.transform(X_test)
モデルをデシジョン ツリーに適合させます。分類子。
from sklearn.tree import DecisionTreeClassifier classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
予測を立てて精度を確認します。
#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))デシジョン ツリー分類器の精度は 91% です。
混同マトリックス
from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred)Output: array([[64,4], [ 2, 30]])
#まず、モデルの予測を視覚化しましょう
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()ログイン後にコピー
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()##次に、このツリーを想像してください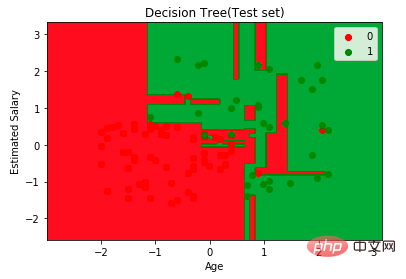
conda install python-graphviz pip install pydotplus
from sklearn.tree import export_graphviz from sklearn.externals.six import StringIO from IPython.display import Image import pydotplusdot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True,feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
在决策树形图中,每个内部节点都有一个分离数据的决策规则。Gini代表基尼系数,它代表了节点的纯度。当一个节点的所有记录都属于同一个类时,您可以说它是纯节点,这种节点称为叶节点。
在这里,生成的树是未修剪的。这棵未经修剪的树不容易理解。在下一节中,我会通过修剪的方式来优化树。
随后优化决策树分类器
criteria: 该选项默认配置是Gini,我们可以通过该项选择合适的属性选择方法,该参数允许我们使用different-different属性选择方式。支持的标准包含基尼指数的“基尼”和信息增益的“熵”。
splitter: 该选项默认配置是" best ",我们可以通过该参数选择合适的分离策略。支持的策略包含“best”(最佳分离)和“random”(最佳随机分离)。
max_depth:默认配置是None,我们可以通过该参数设置树的最大深度。若设置为None,则节点将展开,直到所有叶子包含的样本小于min_samples_split。最大深度值越高,过拟合越严重,反之,过拟合将不严重。
在Scikit-learn中,只有通过预剪枝来优化决策树分类器。树的最大深度可以用作预剪枝的控制变量。
# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))至此分类率提高到94%,相对之前的模型来说,其准确率更高。现在让我们再次可视化优化后的修剪后的决策树。
dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True, feature_names = feature_cols,class_names=['0','1']) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
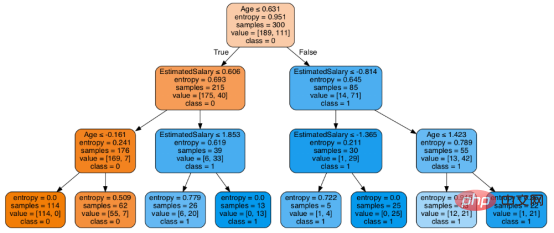
上图是经过修剪后的模型,相对之前的决策树模型图来说,其更简单、更容易解释和理解。
总结
在本文中,我们讨论了很多关于决策树的细节,它的工作方式,属性选择措施,如信息增益,增益比和基尼指数,决策树模型的建立,可视化,并使用Python Scikit-learn包评估和优化决策树性能,这就是这篇文章的全部内容,希望你们能喜欢它。
译者介绍
赵青窕,51CTO社区编辑,从事多年驱动开发。
原文标题:Decision Tree Algorithm, Explained,作者:Nagesh Singh Chauhan
以上がデシジョン ツリー アルゴリズムの構造の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7488
7488
 15
15
 1377
1377
 52
52
 77
77
 11
11
 19
19
 40
40
 オープンソースの無料画像注釈ツールおすすめ 15 選
Mar 28, 2024 pm 01:21 PM
オープンソースの無料画像注釈ツールおすすめ 15 選
Mar 28, 2024 pm 01:21 PM
画像の注釈は、ラベルまたは説明情報を画像に関連付けて、画像の内容に深い意味と説明を与えるプロセスです。このプロセスは機械学習にとって重要であり、画像内の個々の要素をより正確に識別するために視覚モデルをトレーニングするのに役立ちます。画像に注釈を追加することで、コンピュータは画像の背後にあるセマンティクスとコンテキストを理解できるため、画像の内容を理解して分析する能力が向上します。画像アノテーションは、コンピュータ ビジョン、自然言語処理、グラフ ビジョン モデルなどの多くの分野をカバーする幅広い用途があり、車両が道路上の障害物を識別するのを支援したり、障害物の検出を支援したりするなど、幅広い用途があります。医用画像認識による病気の診断。この記事では主に、より優れたオープンソースおよび無料の画像注釈ツールをいくつか推奨します。 1.マケセンス
 この記事では、SHAP: 機械学習のモデルの説明について説明します。
Jun 01, 2024 am 10:58 AM
この記事では、SHAP: 機械学習のモデルの説明について説明します。
Jun 01, 2024 am 10:58 AM
機械学習とデータ サイエンスの分野では、モデルの解釈可能性が常に研究者や実務家に焦点を当ててきました。深層学習やアンサンブル手法などの複雑なモデルが広く適用されるようになったことで、モデルの意思決定プロセスを理解することが特に重要になってきました。 Explainable AI|XAI は、モデルの透明性を高めることで、機械学習モデルに対する信頼と自信を構築するのに役立ちます。モデルの透明性の向上は、複数の複雑なモデルの普及や、モデルを説明するための意思決定プロセスなどの方法によって実現できます。これらの方法には、特徴重要度分析、モデル予測間隔推定、ローカル解釈可能性アルゴリズムなどが含まれます。特徴重要度分析では、入力特徴に対するモデルの影響度を評価することで、モデルの意思決定プロセスを説明できます。モデルの予測間隔の推定
 透明!主要な機械学習モデルの原理を徹底的に分析!
Apr 12, 2024 pm 05:55 PM
透明!主要な機械学習モデルの原理を徹底的に分析!
Apr 12, 2024 pm 05:55 PM
平たく言えば、機械学習モデルは、入力データを予測された出力にマッピングする数学関数です。より具体的には、機械学習モデルは、予測出力と真のラベルの間の誤差を最小限に抑えるために、トレーニング データから学習することによってモデル パラメーターを調整する数学関数です。機械学習には、ロジスティック回帰モデル、デシジョン ツリー モデル、サポート ベクター マシン モデルなど、多くのモデルがあります。各モデルには、適用可能なデータ タイプと問題タイプがあります。同時に、異なるモデル間には多くの共通点があったり、モデル進化の隠れた道が存在したりすることがあります。コネクショニストのパーセプトロンを例にとると、パーセプトロンの隠れ層の数を増やすことで、それをディープ ニューラル ネットワークに変換できます。パーセプトロンにカーネル関数を追加すると、SVM に変換できます。これです
 学習曲線を通じて過学習と過小学習を特定する
Apr 29, 2024 pm 06:50 PM
学習曲線を通じて過学習と過小学習を特定する
Apr 29, 2024 pm 06:50 PM
この記事では、学習曲線を通じて機械学習モデルの過学習と過小学習を効果的に特定する方法を紹介します。過小適合と過適合 1. 過適合 モデルがデータからノイズを学習するためにデータ上で過学習されている場合、そのモデルは過適合していると言われます。過学習モデルはすべての例を完璧に学習するため、未確認の新しい例を誤って分類してしまいます。過適合モデルの場合、完璧/ほぼ完璧なトレーニング セット スコアとひどい検証セット/テスト スコアが得られます。若干修正: 「過学習の原因: 複雑なモデルを使用して単純な問題を解決し、データからノイズを抽出します。トレーニング セットとしての小さなデータ セットはすべてのデータを正しく表現できない可能性があるため、2. 過学習の Heru。」
 宇宙探査と人類居住工学における人工知能の進化
Apr 29, 2024 pm 03:25 PM
宇宙探査と人類居住工学における人工知能の進化
Apr 29, 2024 pm 03:25 PM
1950 年代に人工知能 (AI) が誕生しました。そのとき、研究者たちは、機械が思考などの人間と同じようなタスクを実行できることを発見しました。その後、1960 年代に米国国防総省は人工知能に資金を提供し、さらなる開発のために研究所を設立しました。研究者たちは、宇宙探査や極限環境での生存など、多くの分野で人工知能の応用を見出しています。宇宙探査は、地球を超えた宇宙全体を対象とする宇宙の研究です。宇宙は地球とは条件が異なるため、極限環境に分類されます。宇宙で生き残るためには、多くの要素を考慮し、予防策を講じる必要があります。科学者や研究者は、宇宙を探索し、あらゆるものの現状を理解することが、宇宙の仕組みを理解し、潜在的な環境危機に備えるのに役立つと信じています。
 C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ での機械学習アルゴリズムの実装: 一般的な課題と解決策
Jun 03, 2024 pm 01:25 PM
C++ の機械学習アルゴリズムが直面する一般的な課題には、メモリ管理、マルチスレッド、パフォーマンスの最適化、保守性などがあります。解決策には、スマート ポインター、最新のスレッド ライブラリ、SIMD 命令、サードパーティ ライブラリの使用、コーディング スタイル ガイドラインの遵守、自動化ツールの使用が含まれます。実践的な事例では、Eigen ライブラリを使用して線形回帰アルゴリズムを実装し、メモリを効果的に管理し、高性能の行列演算を使用する方法を示します。
 説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
説明可能な AI: 複雑な AI/ML モデルの説明
Jun 03, 2024 pm 10:08 PM
翻訳者 | Li Rui によるレビュー | 今日、人工知能 (AI) および機械学習 (ML) モデルはますます複雑になっており、これらのモデルによって生成される出力はブラックボックスになっており、関係者に説明することができません。 Explainable AI (XAI) は、利害関係者がこれらのモデルがどのように機能するかを理解できるようにし、これらのモデルが実際に意思決定を行う方法を確実に理解できるようにし、AI システムの透明性、信頼性、およびこの問題を解決するための説明責任を確保することで、この問題を解決することを目指しています。この記事では、さまざまな説明可能な人工知能 (XAI) 手法を検討して、その基礎となる原理を説明します。説明可能な AI が重要であるいくつかの理由 信頼と透明性: AI システムが広く受け入れられ、信頼されるためには、ユーザーは意思決定がどのように行われるかを理解する必要があります
 フラッシュ アテンションは安定していますか?メタとハーバードは、モデルの重みの偏差が桁違いに変動していることを発見しました
May 30, 2024 pm 01:24 PM
フラッシュ アテンションは安定していますか?メタとハーバードは、モデルの重みの偏差が桁違いに変動していることを発見しました
May 30, 2024 pm 01:24 PM
MetaFAIR はハーバード大学と協力して、大規模な機械学習の実行時に生成されるデータの偏りを最適化するための新しい研究フレームワークを提供しました。大規模な言語モデルのトレーニングには数か月かかることが多く、数百、さらには数千の GPU を使用することが知られています。 LLaMA270B モデルを例にとると、そのトレーニングには合計 1,720,320 GPU 時間が必要です。大規模なモデルのトレーニングには、これらのワークロードの規模と複雑さにより、特有のシステム上の課題が生じます。最近、多くの機関が、SOTA 生成 AI モデルをトレーニングする際のトレーニング プロセスの不安定性を報告しています。これらは通常、損失スパイクの形で現れます。たとえば、Google の PaLM モデルでは、トレーニング プロセス中に最大 20 回の損失スパイクが発生しました。数値的なバイアスがこのトレーニングの不正確さの根本原因です。




