皆さんこんにちは、ピーターです~
インターネット上のさまざまな次元削減アルゴリズムに関する情報は不均一で、ほとんどのアルゴリズムではソース コードが提供されていません。これは、Python を使用して、PCA、LDA、MDS、LLE、TSNE などの 11 の古典的なデータ抽出 (データ次元削減) アルゴリズムを実装する GitHub プロジェクトです。関連情報と表示効果が含まれており、機械学習の初心者や初心者に非常に適しています。データマイニングを始めたばかりの方。
いわゆる次元削減とは、ベクトルに含まれる有用な情報を表すために、d の数を持つベクトル Zi のセットを使用することです。 Xi に数字 D を付けます。ここで、d
通常、ほとんどのデータ セットの次元は数百、さらには数千であり、古典的な MNIST の次元はすべて 64 であることがわかります。
MNIST 手書き数字データ セット
しかし、実際のアプリケーションでは、私たちが使用する有用な情報にはそれほど高い次元は必要なく、データの数が増加するたびに、 1 つの次元に必要なサンプルは指数関数的に増加し、これは大規模な「次元災害」に直接つながる可能性があります。データ次元の削減によって次のことが達成できます。
ノイズを除去します。この情報を正しく処理し、次元削減を正確かつ効果的に実行できれば、ノイズの削減に大きく役立ちます。計算量が削減され、機械の稼働効率が向上します。データの次元削減は、テキスト処理、顔認識、画像認識、自然言語処理などの分野でもよく使用されます。
高次元空間のデータはまばらに分散していることが多いため、次元削減のプロセス中に、通常、データの削除が行われます。これらのデータには、冗長データ、無効な情報や重複した表現などは削除されます。
例: 1024*1024 の画像があります。中央の 50*50 の領域を除いて、他の位置はすべてゼロ値です。これらのゼロ情報は役に立たない情報として分類できます。対称グラフィックスの場合、情報の対称的な部分は、繰り返される情報として分類できます。
したがって、ほとんどの古典的な次元削減手法もこの内容に基づいています。次元削減手法は、線形次元削減と非線形次元削減に分けられます。非線形次元削減は、カーネル関数ベースと固有値ベースの手法に分けられます。
に基づくカーネル関数の非線形次元削減法 - KPCA、KICA、KDA
固有値に基づく非線形次元削減法 (フローパターン学習) - ISOMAP、LLE、LE、LPP、LTSA、MVU
Heucoderハルビン工業大学でコンピューター技術を専攻する修士課程の学生である彼は、PCA、KPCA、LDA、MDS、ISOMAP、LLE、TSNE、AutoEncoder、FastICA、SVD、LE、LPP を含む合計 12 の古典的な次元削減アルゴリズムをコンパイルしました。以下では、主に PCA アルゴリズムを例として、次元削減アルゴリズムの具体的な動作を紹介します。
PCA は、高次元空間から低次元空間へのマッピングに基づくマッピング手法であり、最も基本的な教師なし次元削減アルゴリズムでもあります。目標は、データが最も大きく変化する方向、または再構成誤差が最小になる方向に投影することです。これは、1901 年に Karl Pearson によって提案された、線形次元削減手法です。 PCA に関連する原理は、最大分散理論または最小誤差理論と呼ばれることがよくあります。この 2 つは同じ目標を持っていますが、プロセスの焦点が異なります。
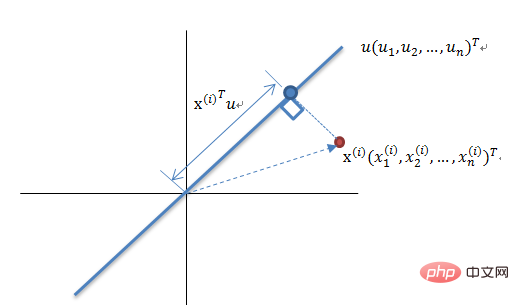
最大分散理論の次元削減原理
N 次元ベクトルのセットを K 次元 (K は 0 より大きく、N より小さい) に削減します。目標は、K 個の単位直交基底があり、各フィールドの COV(X,Y) が 0 で、フィールドの分散ができるだけ大きいことを選択することです。したがって、最大分散は投影データの分散が最大化されていることを意味します。このプロセスでは、データセット Xmxn の最適な投影空間 Wnxk や共分散行列などを見つける必要があります。アルゴリズム フローは次のとおりです:
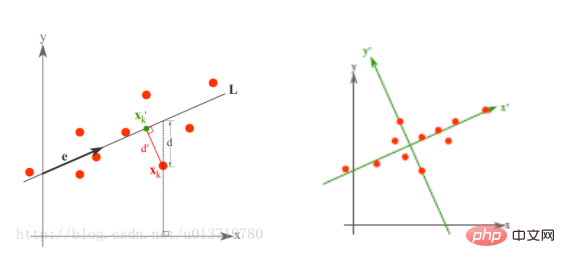最小誤差理論の次元削減原理
最小誤差は平均投影コストを最小にする線形投影であり、その際に二乗誤差評価関数J0(x0)などのパラメータを求める必要があります。
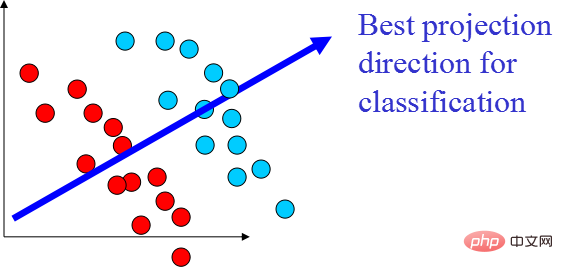
PCA アルゴリズムのコードは次のとおりです:
from __future__ import print_function
from sklearn import datasets
import matplotlib.pyplot as plt
import matplotlib.cm as cmx
import matplotlib.colors as colors
import numpy as np
%matplotlib inline
def shuffle_data(X, y, seed=None):
if seed:
np.random.seed(seed)
idx = np.arange(X.shape[0])
np.random.shuffle(idx)
return X[idx], y[idx]
# 正规化数据集 X
def normalize(X, axis=-1, p=2):
lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
lp_norm[lp_norm == 0] = 1
return X / np.expand_dims(lp_norm, axis)
# 标准化数据集 X
def standardize(X):
X_std = np.zeros(X.shape)
mean = X.mean(axis=0)
std = X.std(axis=0)
# 做除法运算时请永远记住分母不能等于 0 的情形
# X_std = (X - X.mean(axis=0)) / X.std(axis=0)
for col in range(np.shape(X)[1]):
if std[col]:
X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]
return X_std
# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
if shuffle:
X, y = shuffle_data(X, y, seed)
n_train_samples = int(X.shape[0] * (1-test_size))
x_train, x_test = X[:n_train_samples], X[n_train_samples:]
y_train, y_test = y[:n_train_samples], y[n_train_samples:]
return x_train, x_test, y_train, y_test
# 计算矩阵 X 的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
if not Y.any():
Y = X
n_samples = np.shape(X)[0]
covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))
return np.array(covariance_matrix, dtype=float)
# 计算数据集 X 每列的方差
def calculate_variance(X):
n_samples = np.shape(X)[0]
variance = (1 / n_samples) * np.diag((X - X.mean(axis=0)).T.dot(X - X.mean(axis=0)))
return variance
# 计算数据集 X 每列的标准差
def calculate_std_dev(X):
std_dev = np.sqrt(calculate_variance(X))
return std_dev
# 计算相关系数矩阵
def calculate_correlation_matrix(X, Y=np.empty([0])):
# 先计算协方差矩阵
covariance_matrix = calculate_covariance_matrix(X, Y)
# 计算 X, Y 的标准差
std_dev_X = np.expand_dims(calculate_std_dev(X), 1)
std_dev_y = np.expand_dims(calculate_std_dev(Y), 1)
correlation_matrix = np.divide(covariance_matrix, std_dev_X.dot(std_dev_y.T))
return np.array(correlation_matrix, dtype=float)
class PCA():
"""
主成份分析算法 PCA，非监督学习算法.
"""
def __init__(self):
self.eigen_values = None
self.eigen_vectors = None
self.k = 2
def transform(self, X):
"""
将原始数据集 X 通过 PCA 进行降维
"""
covariance = calculate_covariance_matrix(X)
# 求解特征值和特征向量
self.eigen_values, self.eigen_vectors = np.linalg.eig(covariance)
# 将特征值从大到小进行排序，注意特征向量是按列排的，即 self.eigen_vectors 第 k 列是 self.eigen_values 中第 k 个特征值对应的特征向量
idx = self.eigen_values.argsort()[::-1]
eigenvalues = self.eigen_values[idx][:self.k]
eigenvectors = self.eigen_vectors[:, idx][:, :self.k]
# 将原始数据集 X 映射到低维空间
X_transformed = X.dot(eigenvectors)
return X_transformed
def main():
# Load the dataset
data = datasets.load_iris()
X = data.data
y = data.target
# 将数据集 X 映射到低维空间
X_trans = PCA().transform(X)
x1 = X_trans[:, 0]
x2 = X_trans[:, 1]
cmap = plt.get_cmap('viridis')
colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
class_distr = []
# Plot the different class distributions
for i, l in enumerate(np.unique(y)):
_x1 = x1[y == l]
_x2 = x2[y == l]
_y = y[y == l]
class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
# Add a legend
plt.legend(class_distr, y, loc=1)
# Axis labels
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()
if __name__ == "__main__":
main()最後に、次のように次元削減の結果が得られます。その中で、特徴量 (D) がサンプル数 (N) よりもはるかに大きい場合に、ちょっとしたトリックを使用して PCA アルゴリズムの複雑度変換を実装できます。
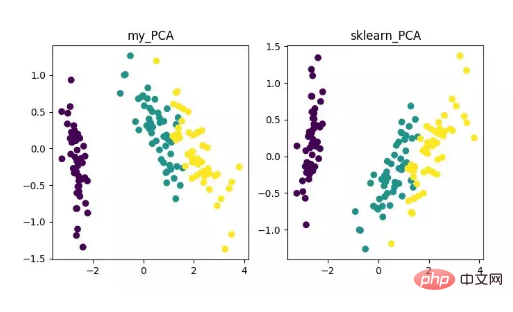
PCA 次元削減アルゴリズムの表示
もちろん、このアルゴリズムは古典的で一般的に使用されていますが、欠点も非常に明らかです。線形相関は非常にうまく除去できますが、高次の相関に直面した場合は効果が乏しく、同時に PCA 実装の前提はデータの主な特徴が直交方向に分布していると仮定することです。非直交方向の場合 分散が大きい方向がいくつかあるため、PCA の効果は大幅に減少します。
KPCA は、カーネル テクノロジと PCA を組み合わせた製品です。違いは、共分散行列を計算するときにカーネル関数が使用されることです。これは、カーネル関数によるマッピング後の共分散行列です。
カーネル関数の導入により、非線形データ マッピングの問題を非常にうまく解決できます。 kPCA は非線形データを高次元空間にマッピングできます。標準 PCA を使用して非線形データを別の低次元空間にマッピングします。
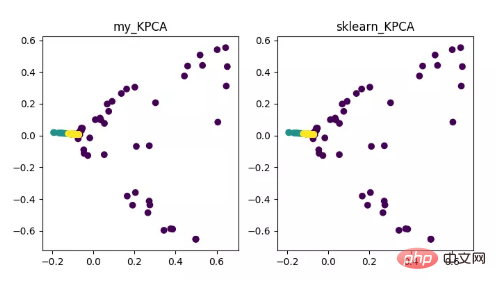
KPCA 次元削減アルゴリズムの表示
コード アドレス:
https://github.com/heucoder/Dimensionity_reduction_alo_codes/blob/master /codes/PCA/KPCA.py
LDA は特徴抽出として使用できるテクノロジーであり、その目標は次のとおりです。クラス間の差異を最大化し、分類などのタスク、つまり異なるクラスのサンプルを効果的に分離することを容易にするために、クラス内差異の方向性の投影を最小限に抑えます。 LDA は、データ分析プロセスの計算効率を向上させ、正則化できないモデルの次元性の障害によって引き起こされる過剰適合を軽減できます。
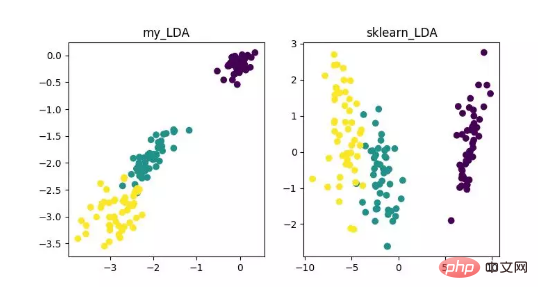
LDA 次元削減アルゴリズムの表示
コード アドレス:
https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master /codes/LDA
MDS は多次元スケーリング分析であり、研究対象の認識や好みを直感的な空間図で表現する手法です。 . 従来の次元削減方法。この方法では、任意の 2 つのサンプル点間の距離を計算し、低次元空間に投影して投影を達成した後も相対距離を維持できるようにします。
sklearn の MDS は反復最適化手法を採用しているため、以下では反復手法と非反復手法の両方を実装します。
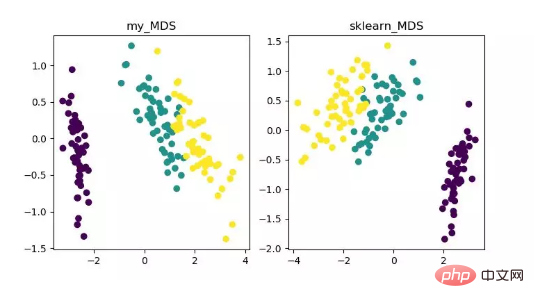
MDS 次元削減アルゴリズムの表示
コード アドレス:
https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master /codes/MDS
Isomap は等尺性マッピング アルゴリズムです。このアルゴリズムは、非線形構造化データ セットに対する MDS アルゴリズムの欠点をうまく解決します。
MDS アルゴリズムでは、次元削減後のサンプル間の距離は変更されませんが、Isomap アルゴリズムでは近傍グラフが導入されます。サンプルは隣接するサンプルにのみ接続され、隣接する点間の距離を計算して、ここに追加されます。次元削減と距離保存に基づいています。
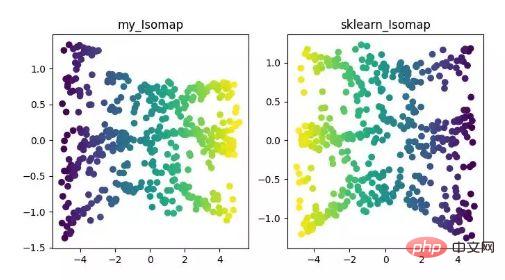
ISOMAP 次元削減アルゴリズムの表示
コード アドレス:
https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master /codes/ISOMAP
LLE(ローカル線形埋め込み)LLE は、非線形次元削減アルゴリズムであるローカル線形埋め込みアルゴリズムです。このアルゴリズムの核となる考え方は、各点は複数の隣接する点の線形結合によって近似的に再構成され、その後、高次元データが低次元空間に投影されて、データ間で局所的な線形再構成が維持されるということです。つまり、同じ再構成係数を持ちます。いわゆる多様体の次元削減を扱う場合、その効果は PCA よりもはるかに優れています。
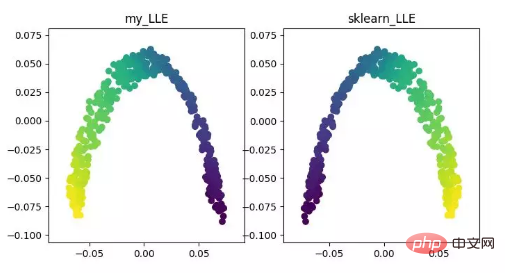
LLE 次元削減アルゴリズムの表示
コード アドレス:
https://github.com/heucoder/Dimensionity_reduction_alo_codes/tree/master/codes/LLE
以上がPython は 12 次元削減アルゴリズムを実装しますの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。
![[Web フロントエンド] Node.js クイック スタート](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
