深層学習の汎化能力について簡単に説明した記事

1. DNN 汎化能力の問題
この論文では主に、なぜ過剰パラメータ化されたニューラル ネットワーク モデルが優れた汎化パフォーマンスを発揮できるのかについて説明しています。つまり、トレーニング セットを単に記憶するのではなく、トレーニング セットから一般的なルールを要約して、テスト セットに適用できるようにします (汎化能力)。

従来のデシジョン ツリー モデルを例に挙げると、ツリー モデルがデータ セットの一般的なルールを学習すると、ツリーが最初にノードを分割する場合は良い状況になります。異なるラベルを持つサンプルを区別するだけで十分で、深さが非常に小さく、対応する各リーフのサンプル数が十分である (つまり、統計ルールに基づくデータ量も比較的大きい) 場合、ルールは次のようになります。他のデータに一般化できる可能性があります。 (つまり、適合性と汎化能力が優れている)。
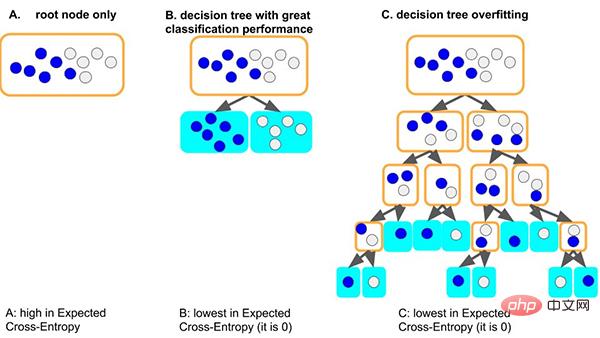
もう 1 つの最悪の状況は、ツリーがいくつかの一般的なルールを学習できない場合、このデータセットを学習するために、ツリーはおそらく葉ごとにますます深くなってしまうことです。ノードは少数のサンプルに対応します (少量のデータによってもたらされる統計情報は単なるノイズである可能性があります) 最後に、すべてのデータは暗記によって記憶されます (つまり、過学習で汎化能力がありません)。深すぎるツリー モデルは簡単にオーバーフィットする可能性があることがわかります。
では、過剰にパラメータ化されたニューラル ネットワークはどのようにして適切な一般化を達成できるのでしょうか?
2. DNN の汎化能力の理由
この記事では、ニューラル ネットワークの勾配降下最適化プロセスにおける汎化能力の理由を探るという、シンプルかつ一般的な観点から説明します:
勾配コヒーレンス理論を要約しました。さまざまなサンプルからの勾配のコヒーレンスが、ニューラル ネットワークが優れた一般化機能を備えている理由です。トレーニング中にさまざまなサンプルの勾配が適切に調整されている場合、つまり、それらがコヒーレントである場合、勾配降下法は安定しており、迅速に収束することができ、結果として得られるモデルは適切に一般化できます。そうしないと、サンプルが少なすぎる場合、またはトレーニング時間が長すぎる場合、一般化できない可能性があります。

この理論に基づいて、次のような説明ができます。
2.1 幅ニューラル ネットワークの一般化
幅広ニューラル ネットワーク モデルには優れた一般化機能があります。これは、より広いネットワークにはより多くのサブネットワークがあり、より小規模なネットワークよりも勾配コヒーレンスが生成される可能性が高く、その結果一般化が向上するためです。言い換えれば、勾配降下法は一般化 (一貫性) 勾配を優先する特徴セレクターであり、より広いネットワークにはより多くの特徴があるため、より優れた特徴がある可能性があります。
- 元の論文: 一般化と幅。Neyshabur et al. [2018b] は、より広いネットワークほどより一般化できることを発見しました。これで説明できますか? 直観的には、より広いネットワークには、任意のレベルでより多くのサブネットワークがあります。つまり、セクション 10 で説明したように、勾配降下法は、よく一般化された (一貫した) 機能では、より広範なネットワークは、より多くの機能を備えているという理由だけで、より優れた機能を備えている可能性があります。これに関連して、宝くじの仮説も参照してください [Frankle and Carbin, 2018]
- 論文リンク: https ://github.com/aialgorithm/Blog
しかし、個人的には、ネットワーク入力層/隠れ層の幅を区別する必要があると思います。特にデータ マイニング タスクの入力層の場合、入力特徴量は通常手動で設計されるため、特徴量の選択を考慮する (入力層の幅を減らすなど) 必要があります。そうでないと、特徴量ノイズを直接入力すると勾配コヒーレンスに干渉します。 . .
2.2 ディープ ニューラル ネットワークの一般化
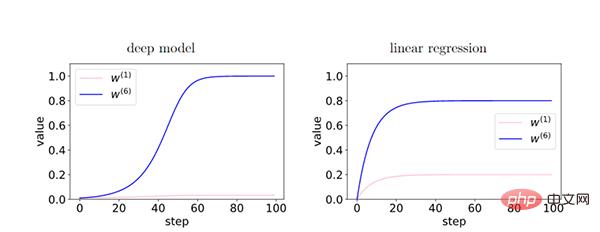
ネットワークが深くなるほど、勾配コヒーレンス現象が増幅され、一般化能力が向上します。

ディープモデルでは、層間のフィードバックによってコヒーレントな勾配が強化されるため、コヒーレントな勾配の特性(W6)とインコヒーレントな勾配の特性(W1間の相対差)が存在します。 ) はトレーニング中に指数関数的に増幅されます。これにより、より深いネットワークではコヒーレントな勾配が優先されるため、一般化機能が向上します。
2.3 早期停止
早期停止を通じて、非コヒーレントな勾配の過度の影響を軽減し、一般化を向上させることができます。
トレーニング中、いくつかの簡単なサンプルは他のサンプル (ハード サンプル) よりも早くフィッティングされます。トレーニングの初期段階では、これらの簡単なサンプルの相関勾配が支配的であり、適合が容易です。学習の後半段階では、困難なサンプルの一貫性のない勾配が平均勾配 g(wt) を支配し、汎化能力が低下するため、この時点で早期に停止する必要があります。

- (注: 単純なサンプルとは、データ セット内に多くの共通の勾配があるサンプルです。このため、ほとんどの勾配はそれに有益です。 、収束
2.4 完全勾配降下法 VS 学習率
完全勾配降下法にも優れた汎化能力があることがわかりました。さらに、注意深い実験では、確率的勾配降下法が必ずしもより良い一般化につながるわけではないことが示されていますが、これは確率的勾配が極小値から飛び出したり、正則化などに役割を果たしたりする可能性を排除するものではありません。
- 私たちの理論に基づくと、有限学習率とミニバッチ確率論は汎化には必要ありません
学習率が低いと汎化誤差は減少しない可能性があると考えていますなぜなら、学習率が低いほど反復回数が増えることを意味するからです(早期停止の反対)。
- 学習率が十分に小さいと仮定すると、トレーニングが進むにつれて汎化ギャップは減少しません。これはトレーニングの反復安定性分析からわかります: さらに 40 ステップでは、安定性は低下するだけです。これに違反すると、実際の設定では、これは理論の興味深い制限を示しています。
2.5 L2 および L1 正則化
L2 および L1 正則化を目的関数に追加し、対応する勾配計算を行います。 , L1 正規項に追加する必要がある勾配はsign(w)、L2 勾配は w です。 L2 正則化を例にとると、対応する勾配 W(i 1) 更新式は次のとおりです。 図
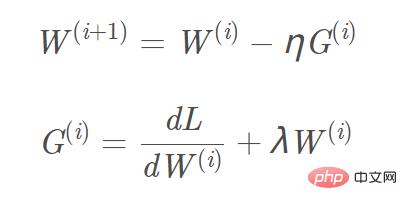
「L2 正則化 (重みの減衰)」は次のように考えることができます。一種の「背景力」により、各パラメーターをデータに依存しないゼロ値に近づけることができます (L1 は疎な解を簡単に取得でき、L2 は 0 に近い滑らかな解を簡単に取得できます)。これにより、弱い勾配方向の影響が排除されます。一貫した勾配方向の場合にのみ、パラメータを「背景力」から相対的に分離でき、データに基づいて勾配の更新を完了できます。

2.6 高度な勾配降下アルゴリズム
- Momentum、Adam およびその他の勾配降下アルゴリズム
Momentum、Adam For等勾配降下アルゴリズムでは、パラメータ W の更新方向は現在の勾配によって決定されるだけでなく、以前に蓄積された勾配の方向にも関連します (つまり、蓄積されたコヒーレント勾配の効果は保持されます)。これにより、勾配方向がわずかに変化する次元ではパラメータの更新が速くなり、勾配方向が大きく変化する次元では更新振幅が小さくなり、収束が促進され発振が低減される効果が得られます。
- 弱い勾配方向での勾配降下の抑制
バッチ勾配降下アルゴリズムを最適化し、汎化機能をさらに向上させることで、弱い勾配方向での勾配更新を抑制できます。たとえば、ウィンザー化勾配降下法を使用して勾配の外れ値を除外し、平均を取ることができます。または、勾配の外れ値の影響を軽減するために、平均の代わりに勾配の中央値を取得します。
概要
記事の最後に一言。深層学習の理論に興味がある場合は、言及されている関連研究を読むことができます。紙の中で。
以上が深層学習の汎化能力について簡単に説明した記事の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7548
7548
 15
15
 1382
1382
 52
52
 83
83
 11
11
 22
22
 90
90
 Python での感情分析に BERT を使用する方法と手順
Jan 22, 2024 pm 04:24 PM
Python での感情分析に BERT を使用する方法と手順
Jan 22, 2024 pm 04:24 PM
BERT は、2018 年に Google によって提案された事前トレーニング済みの深層学習言語モデルです。正式名は BidirectionEncoderRepresentationsfromTransformers で、Transformer アーキテクチャに基づいており、双方向エンコードの特性を備えています。従来の一方向コーディング モデルと比較して、BERT はテキストを処理するときにコンテキスト情報を同時に考慮できるため、自然言語処理タスクで優れたパフォーマンスを発揮します。その双方向性により、BERT は文内の意味関係をより深く理解できるようになり、それによってモデルの表現能力が向上します。事前トレーニングおよび微調整方法を通じて、BERT は感情分析、命名などのさまざまな自然言語処理タスクに使用できます。
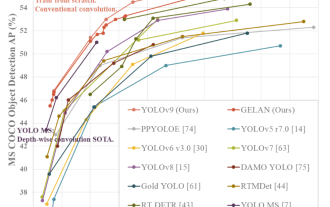 YOLOは不滅です! YOLOv9 がリリースされました: パフォーマンスとスピード SOTA~
Feb 26, 2024 am 11:31 AM
YOLOは不滅です! YOLOv9 がリリースされました: パフォーマンスとスピード SOTA~
Feb 26, 2024 am 11:31 AM
現在の深層学習手法は、モデルの予測結果が実際の状況に最も近くなるように、最適な目的関数を設計することに重点を置いています。同時に、予測に十分な情報を取得するには、適切なアーキテクチャを設計する必要があります。既存の方法は、入力データがレイヤーごとの特徴抽出と空間変換を受けると、大量の情報が失われるという事実を無視しています。この記事では、ディープネットワークを介してデータを送信する際の重要な問題、つまり情報のボトルネックと可逆機能について詳しく説明します。これに基づいて、深層ネットワークが複数の目的を達成するために必要なさまざまな変化に対処するために、プログラマブル勾配情報 (PGI) の概念が提案されています。 PGI は、目的関数を計算するためのターゲット タスクに完全な入力情報を提供することで、ネットワークの重みを更新するための信頼できる勾配情報を取得できます。さらに、新しい軽量ネットワーク フレームワークが設計されています。
 潜在空間の埋め込み: 説明とデモンストレーション
Jan 22, 2024 pm 05:30 PM
潜在空間の埋め込み: 説明とデモンストレーション
Jan 22, 2024 pm 05:30 PM
潜在空間埋め込み (LatentSpaceEmbedding) は、高次元データを低次元空間にマッピングするプロセスです。機械学習と深層学習の分野では、潜在空間埋め込みは通常、高次元の入力データを低次元のベクトル表現のセットにマッピングするニューラル ネットワーク モデルです。このベクトルのセットは、「潜在ベクトル」または「潜在ベクトル」と呼ばれることがよくあります。エンコーディング」。潜在空間埋め込みの目的は、データ内の重要な特徴をキャプチャし、それらをより簡潔でわかりやすい形式で表現することです。潜在空間埋め込みを通じて、低次元空間でデータの視覚化、分類、クラスタリングなどの操作を実行し、データをよりよく理解して活用できます。潜在空間埋め込みは、画像生成、特徴抽出、次元削減など、多くの分野で幅広い用途があります。潜在空間埋め込みがメイン
 ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
以前に書きましたが、今日は、深層学習テクノロジーが複雑な環境におけるビジョンベースの SLAM (同時ローカリゼーションとマッピング) のパフォーマンスをどのように向上させることができるかについて説明します。ここでは、深部特徴抽出と深度マッチング手法を組み合わせることで、低照度条件、動的照明、テクスチャの弱い領域、激しいセックスなどの困難なシナリオでの適応を改善するように設計された多用途のハイブリッド ビジュアル SLAM システムを紹介します。当社のシステムは、拡張単眼、ステレオ、単眼慣性、ステレオ慣性構成を含む複数のモードをサポートしています。さらに、他の研究にインスピレーションを与えるために、ビジュアル SLAM と深層学習手法を組み合わせる方法も分析します。公開データセットと自己サンプリングデータに関する広範な実験を通じて、測位精度と追跡堅牢性の点で SL-SLAM の優位性を実証しました。
 1 つの記事で理解: AI、機械学習、ディープラーニングのつながりと違い
Mar 02, 2024 am 11:19 AM
1 つの記事で理解: AI、機械学習、ディープラーニングのつながりと違い
Mar 02, 2024 am 11:19 AM
今日の急速な技術変化の波の中で、人工知能 (AI)、機械学習 (ML)、および深層学習 (DL) は輝かしい星のようなもので、情報技術の新しい波をリードしています。これら 3 つの単語は、さまざまな最先端の議論や実践で頻繁に登場しますが、この分野に慣れていない多くの探検家にとって、その具体的な意味や内部のつながりはまだ謎に包まれているかもしれません。そこで、まずはこの写真を見てみましょう。ディープラーニング、機械学習、人工知能の間には密接な相関関係があり、進歩的な関係があることがわかります。ディープラーニングは機械学習の特定の分野であり、機械学習
 超強い!深層学習アルゴリズムのトップ 10!
Mar 15, 2024 pm 03:46 PM
超強い!深層学習アルゴリズムのトップ 10!
Mar 15, 2024 pm 03:46 PM
2006 年にディープ ラーニングの概念が提案されてから、ほぼ 20 年が経過しました。ディープ ラーニングは、人工知能分野における革命として、多くの影響力のあるアルゴリズムを生み出してきました。では、ディープラーニングのトップ 10 アルゴリズムは何だと思いますか?私の考えでは、ディープ ラーニングのトップ アルゴリズムは次のとおりで、いずれもイノベーション、アプリケーションの価値、影響力の点で重要な位置を占めています。 1. ディープ ニューラル ネットワーク (DNN) の背景: ディープ ニューラル ネットワーク (DNN) は、多層パーセプトロンとも呼ばれ、最も一般的なディープ ラーニング アルゴリズムです。最初に発明されたときは、コンピューティング能力のボトルネックのため疑問視されていました。最近まで長年にわたる計算能力、データの爆発的な増加によって画期的な進歩がもたらされました。 DNN は、複数の隠れ層を含むニューラル ネットワーク モデルです。このモデルでは、各層が入力を次の層に渡し、
 1.3ミリ秒には1.3ミリ秒かかります。清華社の最新オープンソース モバイル ニューラル ネットワーク アーキテクチャ RepViT
Mar 11, 2024 pm 12:07 PM
1.3ミリ秒には1.3ミリ秒かかります。清華社の最新オープンソース モバイル ニューラル ネットワーク アーキテクチャ RepViT
Mar 11, 2024 pm 12:07 PM
論文のアドレス: https://arxiv.org/abs/2307.09283 コードのアドレス: https://github.com/THU-MIG/RepViTRepViT は、モバイル ViT アーキテクチャで優れたパフォーマンスを発揮し、大きな利点を示します。次に、この研究の貢献を検討します。記事では、主にモデルがグローバル表現を学習できるようにするマルチヘッド セルフ アテンション モジュール (MSHA) のおかげで、軽量 ViT は一般的に視覚タスクにおいて軽量 CNN よりも優れたパフォーマンスを発揮すると述べられています。ただし、軽量 ViT と軽量 CNN のアーキテクチャの違いは十分に研究されていません。この研究では、著者らは軽量の ViT を効果的なシステムに統合しました。
 AlphaFold 3 が発売され、タンパク質とすべての生体分子の相互作用と構造をこれまでよりもはるかに高い精度で包括的に予測します。
Jul 16, 2024 am 12:08 AM
AlphaFold 3 が発売され、タンパク質とすべての生体分子の相互作用と構造をこれまでよりもはるかに高い精度で包括的に予測します。
Jul 16, 2024 am 12:08 AM
エディター | Radish Skin 2021 年の強力な AlphaFold2 のリリース以来、科学者はタンパク質構造予測モデルを使用して、細胞内のさまざまなタンパク質構造をマッピングし、薬剤を発見し、既知のあらゆるタンパク質相互作用の「宇宙地図」を描いてきました。ちょうど今、Google DeepMind が AlphaFold3 モデルをリリースしました。このモデルは、タンパク質、核酸、小分子、イオン、修飾残基を含む複合体の結合構造予測を実行できます。 AlphaFold3 の精度は、これまでの多くの専用ツール (タンパク質-リガンド相互作用、タンパク質-核酸相互作用、抗体-抗原予測) と比較して大幅に向上しました。これは、単一の統合された深層学習フレームワーク内で、次のことを達成できることを示しています。