グラフ理論は実際に始めるのは難しくありません
長年のプログラミング経験を持つ開発者にとって、グラフの概念は馴染みのないものではありません。多くのトップ企業は技術面接でグラフ理論の理解をテストします。実際、開発者はこれらの概念を利用するために高度な問題に対処する必要はありません。これを理解するには、まずグラフが人気のデータ構造である理由と、それをコードに実装する方法を確認します。
リレーショナル モデル
コーディングの経験に関係なく、開発者は配列と辞書のデータ型をある程度理解している必要があります。これらのコレクションは、ほとんどの言語で使用される標準概念であり、リストベースのコンテンツをレンダリングするときにうまく機能します。

ほとんどの場合、リストはデータベースから取得されるか、データベースに基づいて取得されます。 REST クエリで情報を表示するための完璧なソリューション。ただし、場合によっては、相互に関連するコンテキストを持つレコードをリストで提供する必要があります。この時点で、データをグラフに整理すると便利になります。
図の主な目的は、情報をリストすることではなく (これは可能ですが)、オブジェクト間の関係を定義することです。オブジェクト間の関係を定義することがなぜ役立つのでしょうか?次の例を見てみましょう。

2 つの頂点と 1 つの辺を持つ無向グラフ
(1) マップ アプリケーション:
技術面接で質問されたら、マッピング サービス (Apple や Google マップなど) を再作成するためにデータをどのように整理しますか?データベース内のすべての既知の道路のリストを提供することに加えて、作成するモデルでは、時間帯、交通量、一方通行などの要因に基づいて、目的地に到達する最適な方法を決定する必要があります。この大量のデータを機能させるには、モデル内の道路と他のすべての道路との関係を知る必要があります。
(2) ソーシャルメディア :
ソーシャルメディアの価値は通常、ユーザーをフォローまたはフォローしているユーザーの数によって測定されます。 Twitter などのオンライン プラットフォームを使用すると、ユーザーは誰とでもつながり、最新情報を受け取ることができるため、多くのユーザーが集まります。
受信者がユーザーの接続リクエストを受け入れない限り、ユーザーはユーザーのネットワークにユーザーを追加できないため、LinkedIn モデルはより詳細です。この場合、LinkedIn 接続は双方向の関係を表します。これに沿って、ユーザーは自分のネットワークを検索して、希望する仕事の機会に関連する人がいるかどうかを確認することもできます。この文脈において、「ネットワーク」は直接的または間接的な接続を意味する場合があります。このような強力なモデルは、単純なリストに基づいているだけではなく、すべてのプロファイルがどのように関連しているかを判断するインテリジェンスが含まれています。
グラフィック コンポーネント
グラフが日常のアプリケーションでどのように使用されるかを理解したところで、グラフのコンポーネントを紹介しましょう。
グラフ内のノードは頂点と呼ばれます。グラフは単一の頂点として構築できますが、複数の頂点を含むモデルは現実世界のアプリケーションをより適切に表現します。
グラフ内のオブジェクトは、エッジと呼ばれる接続を通じて相互に関連しています。
ニーズに応じて、頂点をエッジを介して 1 つまたは複数のオブジェクトに接続することも、エッジのない頂点を作成することもできます。
最後に、スタックやキューなどの他の標準構造とは異なり、グラフには通常、指定された開始点や終了点がありません。グラフ構成の例をいくつか示します。

2 つの頂点と 1 つのエッジを持つ無向グラフ
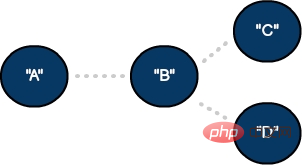
2 つの頂点と 1 つの辺を持つ無向グラフ
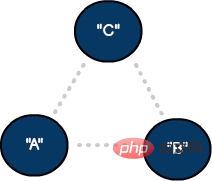
無向を使用した無向グラフ2 つの頂点と 1 つのエッジを持つグラフ
有向グラフと無向グラフ
無向グラフでは、ソース頂点と宛先間の接続は等しいです。これらのモデルは、地図アプリケーションにおける双方向道路と同様の、双方向接続を表します。
一方向の接続を定義するには、線と矢印を使用してモデルを有向グラフに更新します。
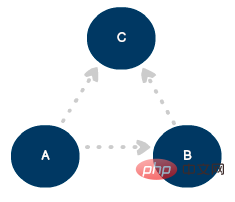
3 つの頂点と 3 つの頂点エッジの有向グラフ
接続レベル
グラフ内の頂点間の接続の程度を表現する必要がある場合があります。この手法は、ノード間の距離、時間、重大度を定量化する場合に有効です。 重みは通常エッジに関連しており、追跡に使用される比較変数です。 。
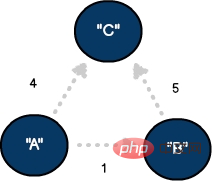
#3 つの頂点と 3 つのエッジを持ち、エッジに重みが付けられている有向グラフ
グラフの頂点
グラフ理論の基本を理解したところで、これらのモデルをコードで複製する方法を見てみましょう。以下では、カスタム ジェネリック オブジェクト (T) をサポートする頂点を作成します。 tvalue 変数は、単一の文字列、int、またはカスタム型 (たとえば、通りの名前やソーシャル メディア プロフィール) など、その型によって保持されるデータを表します。
また、型が一般的な Equatable プロトコル (Swift) に準拠するように注意してください。これにより、必要に応じて特定の頂点インスタンスが等しいかどうかを比較できるようになります。
public class Vertex <t> : Equatable {<br><br>var tvalue: T?<br>var neighbors = Array<edge>>()<br>let uuid = UUID()<br><br>public init(with name: T) {<br>self.tvalue = name<br>}<br><br>//equatable conformance<br>public static func == (lhs: Vertex, rhs: Vertex) -> Bool {<br> return lhs.uuid == rhs.uuid<br>}<br>}</edge></t>
隣接リスト
隣接リストは、他の頂点との接続を表します。前述したように、各頂点は 1 つ以上の隣接する頂点に接続できます。この関係のリストは「隣接リスト」と呼ばれることもあり、多くの高度な問題を解決するために使用できます。
var neighbors = Array<edge>>()</edge>
グラフ エッジ
頂点を作成するときに、カスタム エッジ タイプの配列を保存するための隣接プロパティを追加しました。下側のエッジは、後続の隣接する頂点とその潜在的なエッジの重みの参照を提供します。
public class Edge <t> {<br><br>var neighbor: Vertex<t><br>var weight: Int<br><br>init() {<br> weight = 0<br> self.neighbor = Vertex<t>()<br>}<br>}</t></t></t>キャンバスの構築
頂点オブジェクトとエッジ オブジェクトを用意したら、グラフィック キャンバスと呼ばれる中央の記憶構造にそれらを追加できます。私たちのキャンバスは技術的には配列ですが、私たちの目標は、コレクションを一連の関係として視覚化することです。 addVertex 関数を使用すると、単一の汎用頂点をキャンバスに追加できます。一方、addEdge メソッドはエッジに必要な参照情報を提供します。
最後に、エッジはソース頂点隣接リストに追加されるだけであるため、コードはグラフが方向付けられていることを前提としています。
rreeee要約すると、グラフに関する知識を紹介し、グラフを使用してオブジェクト間の関係を表現する方法を確認しました。また、グラフを構成するいくつかの方法と、さまざまなモデルを記述するために使用されるコンポーネントについても確認しました。
モデルを定義した後、グラフ ナビゲーションや幅優先検索などのトラバーサル アルゴリズムなど、より高度な機能の基礎を築きます。
翻訳者紹介
Kang Shaojing、51CTO コミュニティ編集者、現在通信業界で低レベルドライバー開発の職に従事し、データ構造と Python を勉強し、現在はオペレーティング システムに興味を持っています。データベースおよびその他の関連分野。
元のタイトル: グラフ理論の完全初心者ガイド、著者: Wayne Bishop
リンク:
https://stackoverflow.blog/2022/05/26/the -グラフ理論への完全初心者ガイド/
以上がグラフ理論は実際に始めるのは難しくありませんの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7536
7536
 15
15
 1379
1379
 52
52
 82
82
 11
11
 21
21
 86
86
 カーソルAIでバイブコーディングを試してみましたが、驚くべきことです!
Mar 20, 2025 pm 03:34 PM
カーソルAIでバイブコーディングを試してみましたが、驚くべきことです!
Mar 20, 2025 pm 03:34 PM
バイブコーディングは、無限のコード行の代わりに自然言語を使用してアプリケーションを作成できるようにすることにより、ソフトウェア開発の世界を再構築しています。 Andrej Karpathyのような先見の明に触発されて、この革新的なアプローチは開発を許可します
 2025年2月のトップ5 Genai発売:GPT-4.5、Grok-3など!
Mar 22, 2025 am 10:58 AM
2025年2月のトップ5 Genai発売:GPT-4.5、Grok-3など!
Mar 22, 2025 am 10:58 AM
2025年2月は、生成AIにとってさらにゲームを変える月であり、最も期待されるモデルのアップグレードと画期的な新機能のいくつかをもたらしました。 Xai’s Grok 3とAnthropic's Claude 3.7 SonnetからOpenaiのGまで
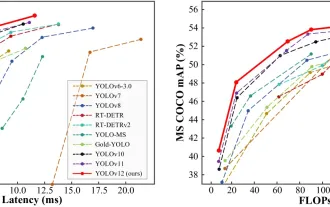 オブジェクト検出にYolo V12を使用する方法は?
Mar 22, 2025 am 11:07 AM
オブジェクト検出にYolo V12を使用する方法は?
Mar 22, 2025 am 11:07 AM
Yolo(あなたは一度だけ見ています)は、前のバージョンで各反復が改善され、主要なリアルタイムオブジェクト検出フレームワークでした。最新バージョンYolo V12は、精度を大幅に向上させる進歩を紹介します
 クリエイティブプロジェクトのための最高のAIアートジェネレーター(無料&amp;有料)
Apr 02, 2025 pm 06:10 PM
クリエイティブプロジェクトのための最高のAIアートジェネレーター(無料&amp;有料)
Apr 02, 2025 pm 06:10 PM
この記事では、トップAIアートジェネレーターをレビューし、その機能、創造的なプロジェクトへの適合性、価値について説明します。 Midjourneyを専門家にとって最高の価値として強調し、高品質でカスタマイズ可能なアートにDall-E 2を推奨しています。
 ChatGpt 4 oは利用できますか?
Mar 28, 2025 pm 05:29 PM
ChatGpt 4 oは利用できますか?
Mar 28, 2025 pm 05:29 PM
CHATGPT 4は現在利用可能で広く使用されており、CHATGPT 3.5のような前任者と比較して、コンテキストを理解し、一貫した応答を生成することに大幅な改善を示しています。将来の開発には、よりパーソナライズされたインターが含まれる場合があります
 chatgptよりも優れたAIはどれですか?
Mar 18, 2025 pm 06:05 PM
chatgptよりも優れたAIはどれですか?
Mar 18, 2025 pm 06:05 PM
この記事では、Lamda、Llama、GrokのようなChatGptを超えるAIモデルについて説明し、正確性、理解、業界への影響における利点を強調しています(159文字)
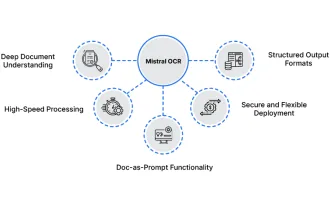 次のラグモデルにミストラルOCRを使用する方法
Mar 21, 2025 am 11:11 AM
次のラグモデルにミストラルOCRを使用する方法
Mar 21, 2025 am 11:11 AM
Mistral OCR:マルチモーダルドキュメントの理解により、検索された世代の革命を起こします 検索された生成(RAG)システムはAI機能を大幅に進めており、より多くの情報に基づいた応答のために膨大なデータストアにアクセスできるようになりました
 トップAIライティングアシスタントは、コンテンツの作成を後押しします
Apr 02, 2025 pm 06:11 PM
トップAIライティングアシスタントは、コンテンツの作成を後押しします
Apr 02, 2025 pm 06:11 PM
この記事では、Grammarly、Jasper、Copy.ai、Writesonic、RytrなどのトップAIライティングアシスタントについて説明し、コンテンツ作成のためのユニークな機能に焦点を当てています。 JasperがSEOの最適化に優れているのに対し、AIツールはトーンの維持に役立つと主張します




