Python を使用して RSA 暗号化と復号化を実装する

昨日、Python を使用して RSA アルゴリズムを実装する方法を示した英語の記事 [1] を見ました。コードのロジックは、前の記事「RSA アルゴリズムを理解する」と同じです。RSA に詳しくない友人でも読むことができます。記事「Understanding the RSA Algorithm.」は、RSA とは何か、RSA の数学的原理を説明し、簡単な例を示しており、Quanzhihu で RSA を理解するのに最も簡単な記事と言えます (これは読者のコメントから来ています)。

英語で提供されたコードを実行したところ、中国語を暗号化できないことが判明したため、中国語の暗号化と復号化をサポートするように暗号化と復号化の関数を修正しました。今日の記事では、Python を使用して RSA 暗号化および復号化プロセスを実装する方法を共有し、RSA を直感的に理解できるようにします。コード内のランダムな素数生成アルゴリズムも学ぶ価値があります。

0. 効果デモ

まずは効果を見てみましょう。

原文：「モグラがいます、取引を終了します」

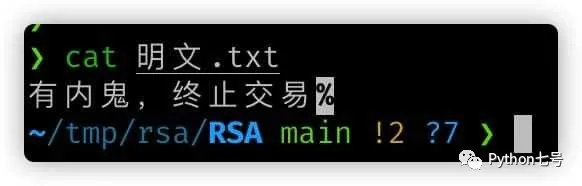
暗号文は全く解読できません：

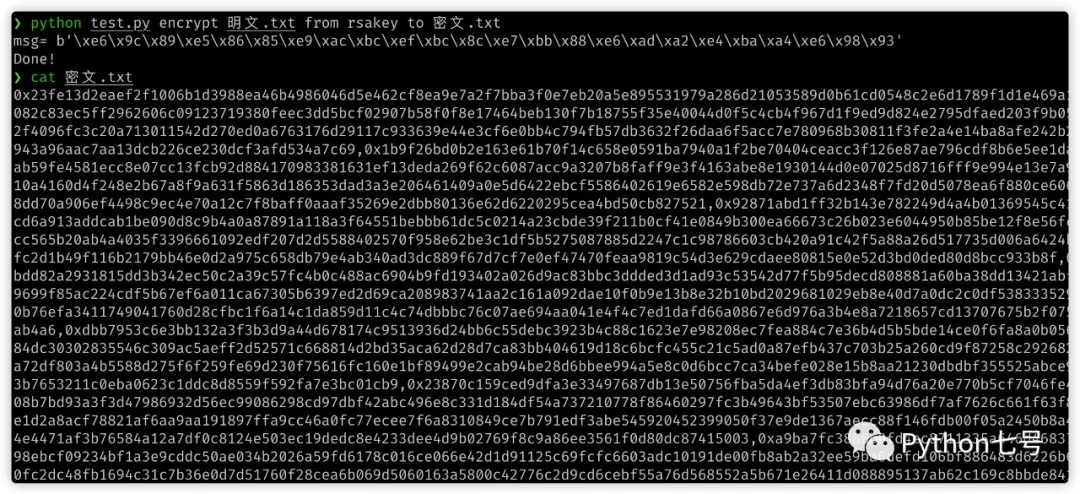
復号後:

完全なコード公開アカウント「Python No. 7」は、「rsa」と返信することで取得できます。

1. 鍵ペアの生成

アイデア:

1) ランダムに 2 つの素数 (素数) p と q を見つけます。p と q が大きいほど安全です。ここでは 1024 ビットの素数を選択します:

p = genprime(1024)
q = genprime(1024)

genprime() 関数の実装プロセスについては触れません。

2) それらの積 n = p * q とオイラー関数 lambda_n を計算します。

n = p * q
lambda_n = (p - 1) * (q - 1)

3) 整数 e をランダムに選択します。条件は 1 < e < lambda_n で、e と lambda_n は互いに素です。たとえば、35537 を選択した場合、35537 には 16 ビットしかなく、lambda_n より小さい必要があります。 < e < lambda_n，且 e 与 lambda_n 互质。比如选择 35537，35537 只有 16 位，必然小于 lambda_n。

e = 35537

4) e * d を lambda_n で割った余りが 1 になるような整数 d を見つけ、キー ペアを返します。

d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)

eucalg 関数の実装については後で説明します。

この時点で、キー ペア生成関数は次のとおりです:

def create_keys():
 p = genprime(1024)
 q = genprime(1024)
 n = p * q
 lambda_n = (p - 1) * (q - 1)
 e = 35537
 d = eucalg(e, lambda_n)[0]
 if d < 0: d += lambda_n
 return (d, n), (e, n)

2. 暗号化と復号化の実装

暗号化と復号化のプロセスは同じ、公開キーです。暗号化、秘密鍵暗号化、鍵復号、その逆の秘密鍵暗号、公開鍵復号がありますが、前者を暗号化、後者を署名と呼びます。

具体的な関数の実装は次のとおりです:

def encrypt_data(data,key):
e_data = []
for d in data:
 e = modpow(d, key[0], key[1]) 
 e_data.append(e)
return e_data

## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data

ここでは modpow 関数が使用されており、式 b^e % n = r を計算するために使用されます。

• 暗号化プロセスの場合、b は平文、(n,e) は公開鍵、r は暗号文です。
• これが復号化プロセスの場合、b は暗号文、(n, d) は秘密鍵、r は有名なテキストです。

modpow は次のように定義されます:

def modpow(b, e, n):
 # find length of e in bits
 tst = 1
 siz = 0
 while e >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the result
 r = 1
 for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
 return r

3. ランダムな素数の生成関数

行列乗算とフィボナッチ数列を使用したランダムな素数の生成関数アルゴリズムに対する数学の重要性を示しています。

# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
 mr = [[0 for j in range(w)] for i in range(w)]
 for i in range(w):
for j in range(w):
 for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
 return mr

# fibonacci calculator
def fib(x, mod):
 if x < 3: return 1
 x -= 2
 # find length of e in bits
 tst = 1
 siz = 0
 while x >= tst:
tst <<= 1
siz += 1
 siz -= 1
 # calculate the matrix
 fm = [
# function matrix
[0, 1],
[1, 1]
 ]
 rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
 ]
 for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
 rm = sqmatrixmul(rm, fm, 2, mod)

 # second row of resulting vector is result
 return (rm[1][0] + rm[1][1]) % mod

def genprime(siz):
 while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
 return num

4. eucalg 関数の実装

関数の本質は、次の 2 つの変数の線形方程式の解を見つけることです:

e * x - lambda_n * y =1

具体的なコード:

def eucalg(a, b):
 # make a the bigger one and b the lesser one
 swapped = False
 if a < b:
a, b = b, a
swapped = True
 # ca and cb store current a and b in form of
 # coefficients with initial a and b
 # a' = ca[0] * a + ca[1] * b
 # b' = cb[0] * a + cb[1] * b
 ca = (1, 0)
 cb = (0, 1)
 while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
 if swapped:
return (ca[1], ca[0])
 else:
return ca

5 、test

test.py スクリプトの使用方法:

1)、キーを生成

python test.py make-keys rsakey

公開キーは rsakey.pub に保存され、秘密キーは rsakey.priv 中

2 に保存されます)、ファイルの内容を暗号化します

プレーン テキスト .txt ファイルがある場合:

python test.py encrypt 明文.txt from rsakey to 密文.txt

は暗号文を生成します.txt

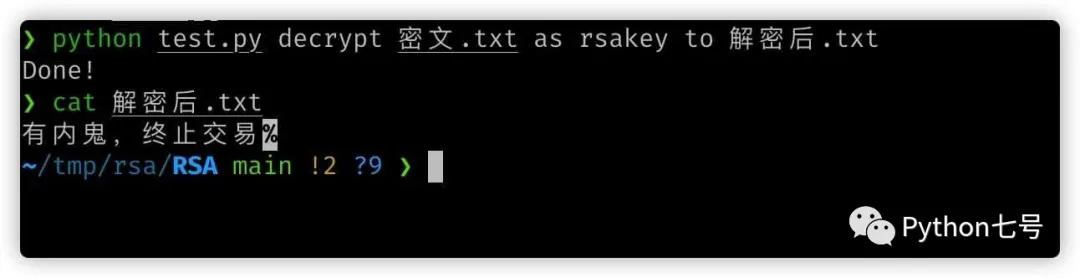
3. ファイルを暗号化します コンテンツの復号化

ファイル ciphertext.txt:

python test.py decrypt 密文.txt as rsakey to 解密后.txt

がある場合は、復号化された .txt

Final が生成されます。言葉

この記事では、RSA アルゴリズムの Python について説明します。簡単な実装は、RSA アルゴリズムを理解するのに役立ちます。

以上がPython を使用して RSA 暗号化と復号化を実装するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。