
この記事は、Byte Education-Adult and Innovation Front-end Team のメンバーによる記事であり、ELab によって公開が許可されています。
この記事では、機械学習やコサイン類似度判定法などを用いてマウスジェスチャ認識方式を設計・検証し、それを三次元空間へ拡張することを試みます。
端末テクノロジーの中核となる内容は、ユーザー インタラクションに直接応答することです。基本的なロジックは、特定のプラットフォームにはいくつかの事前定義されたインタラクション イベントがあり、ユーザーの特定のインタラクション アクションが対応するインタラクション イベントをトリガーするというものです。ユーザー製品のインタラクションデザイン全体もこれに基づいています。優れたユーザーエクスペリエンスを実現するには、便利なインタラクションが必要です。
PC シナリオでは、マウス (トラックパッド) はキーボードのほかに最も重要な入力デバイスです。一般的なマウス操作はマウスのボタンとホイールであるため、対応する一般的なインタラクション イベントはクリック、スクロールです。これらの操作にはオブジェクト (ボタンのクリック、コンテンツ領域またはビューポート全体のスクロール、画像のドラッグなど) が必要であり、ショートカット キーほど便利ではありません。ただし、特定のシナリオではショートカット キーはマウスほど便利ではないため、マウスにもショートカット操作があることが期待されます。マウスジェスチャーは比較的ニッチですが便利で使いやすいショートカット操作です。一般的なマウス ジェスチャには、直線を描く、ティックする、円を描くなどがあります。数百のブラウザが隆盛を極めた初期、国内の多くのブラウザは、競合優位性を差別化するために、便利なマウスジェスチャー操作を大きなセールスポイントとして利用していましたが、ジェスチャー操作は徐々に広く支持され、応用され、静かに市場を開拓してきました。そしてユーザーの習慣。
モバイル タッチ スクリーンのシナリオでは、ジェスチャー操作の利点がより明白です。ジェスチャー操作は、古典的な「左にスワイプして戻る」、「右にスワイプして進む」、「上にスワイプして戻る」に進化しました。ホームページ」、および「下にスワイプして更新」/通知の呼び出し/コントロール センターの呼び出し」。
近年のVR/AR/MRの台頭により、3次元空間でのジェスチャー操作がさらに促進・応用されています。
したがって、マウス ジェスチャの認識を実現するために PC 側を例として取り上げ、インタラクティブ ジェスチャのコア実装ロジックを明確にし、類推して、ソリューションをより多くの端末シナリオに拡張しようとします。
移動とズームは変形されません。つまり、ジェスチャ パスの全体的な位置とサイズは重要ではありません。
ユーザーの繰り返されるジェスチャに対して、ある程度の耐性があります。
この問題の特別な側面は、不確実性の処理にあり、ユーザーが描くマウス ジェスチャには不確実性があります。
標準パスが事前に設定されている場合、問題は「事前に設定された決定的なパス」と「ユーザー入力の不確実なパス」の間の類似性を検出することに変換されます。
ユーザー定義のパスの場合、問題は「ユーザーが設定した不確実なパス」と「ユーザーが入力した不確実なパス」の間の類似性を検出することに変換されます。
従来のプログラミング モデルに従う場合は、厳密なプログラム ロジックを要求し、条件判断のための明確なルールを設定し、この不確実性を正確に測定する必要があります。つまり、二つのパスを代入することで、似ているかどうかの結果が得られるという「魔法の操作」が必要なのです。
ジェスチャ自体に関しては、通常のラスター画像またはベクターグラフィックとして考えることができます。ラスター イメージの場合、画像の内容を理解していなくても、従来の機械学習手法を使用して画像の分類を決定できます。ベクトル グラフィックスの場合は、特別なデータ構造を定義し、グラフィックスの類似性の表現を詳しく調べる必要があります。次回の実装はこの 2 つのアイデアから始まります。
まずは考え方を変える必要があります。機械学習プログラミングは、従来のプログラミングの考え方とはまったく異なります。先ほども述べたように、従来のプログラミングでは条件判定やループなどのプログラムロジックを手作業で正確に指定してコーディングする必要がありました。機械学習プログラミングは、詳細な論理ルールを定式化して記述することにこだわるのではなく、ニューラル ネットワークを構築してコンピューターに機能を学習させます。
機械学習の鍵は、大規模で信頼性の高いデータ セットです。このラベル付け作業は非常に時間がかかります。実現可能性を検証するために、類似の手書き数字データ セット mnist を使用して実際のジェスチャ シーンを置き換えます。 。
したがって、次のステップは次のとおりです:
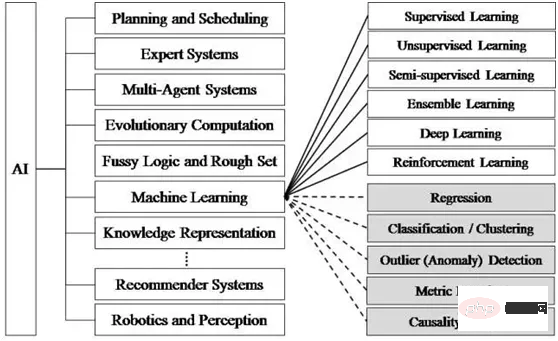
機械学習には多くのアルゴリズムとモデルがあり、さまざまな分野に応じて選択する必要があります。 Tensorflow.js は一連の事前トレーニング済みモデル [1] を公式に提供しており、直接使用することも、再トレーニングして使用することもできます。
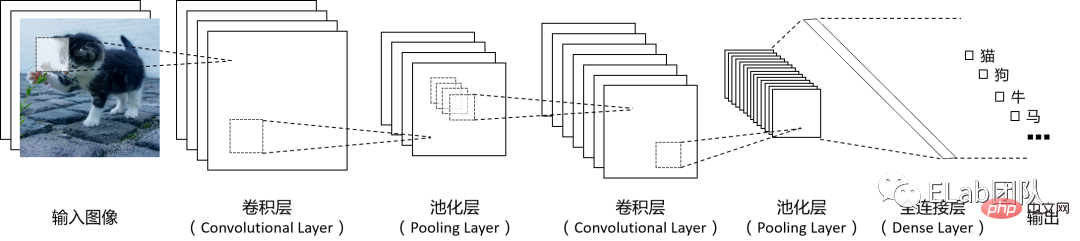
畳み込みニューラル ネットワーク (CNN) は、特にラスター特性を持つ画像やその他のデータを処理する場合に広く使用されている機械学習モデルです。情報処理中、CNN はピクセルの行と列の空間構造を入力として受け取り、複数の数学的計算レイヤーを通じて特徴を抽出し、信号を特徴ベクトルに変換して従来のニューラル ネットワークの構造に接続します。 、画像 従来のニューラル ネットワークに提供される場合、対応する特徴ベクトルは小さくなり、それに応じてトレーニングする必要があるパラメーターの数が減ります。畳み込みニューラル ネットワークの基本的な動作原理図は次のとおりです (図内の各層の数は必要に応じて設計できます):
Tensorflow.js フレームワーク これが私たちの推奨フレームワークとなる理由は、次の利点によるものです:
優れた移植性: Tensorflow.js は最も人気があり効率的な機械学習フレームワークではありませんが、ベースにしているためです。 JSとすぐに使えるAPIを使用しているため、JSをサポートするさまざまな端末で実行およびデプロイするのに便利です。
低遅延と高いプライバシー: 完全にエンド側で実行できるため、検証データをサーバーに送信してサーバーの応答を待つ必要がなく、低遅延という利点があります。遅延と高いセキュリティ。
学習/デバッグのコストが低い: WEB 開発者にとって開始コストが低く、ブラウザーでマシンのトレーニング プロセスを適切に視覚化できます。
TFJS [2] の環境設定は非常に簡単なのでここでは省略します。
この簡単な例を通じて機械学習プログラミングのアイデアを体験し、Tensorflow.js の API に慣れることができます。
データセット
/** * @license* Copyright 2018 Google LLC. All Rights Reserved. * Licensed under the Apache License, Version 2.0 (the "License"); * you may not use this file except in compliance with the License. * You may obtain a copy of the License at * * http://www.apache.org/licenses/LICENSE-2.0 * * Unless required by applicable law or agreed to in writing, software * distributed under the License is distributed on an "AS IS" BASIS, * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. * See the License for the specific language governing permissions and * limitations under the License. * ============================================================================= */
const IMAGE_SIZE = 784;
const NUM_CLASSES = 10;
const NUM_DATASET_ELEMENTS = 65000;
const NUM_TRAIN_ELEMENTS = 55000;
const NUM_TEST_ELEMENTS = NUM_DATASET_ELEMENTS - NUM_TRAIN_ELEMENTS;
const MNIST_IMAGES_SPRITE_PATH =
'https://storage.googleapis.com/learnjs-data/model-builder/mnist_images.png';
const MNIST_LABELS_PATH =
'https://storage.googleapis.com/learnjs-data/model-builder/mnist_labels_uint8';
/** * A class that fetches the sprited MNIST dataset and returns shuffled batches. * * NOTE: This will get much easier. For now, we do data fetching and * manipulation manually. */export class MnistData {
constructor() {
this.shuffledTrainIndex = 0;
this.shuffledTestIndex = 0;
}
async load() {
// Make a request for the MNIST sprited image.const img = new Image();
const canvas = document.createElement('canvas');
const ctx = canvas.getContext('2d');
const imgRequest = new Promise((resolve, reject) => {
img.crossOrigin = '';
img.onload = () => {
img.width = img.naturalWidth;
img.height = img.naturalHeight;
const datasetBytesBuffer =
new ArrayBuffer(NUM_DATASET_ELEMENTS * IMAGE_SIZE * 4);
const chunkSize = 5000;
canvas.width = img.width;
canvas.height = chunkSize;
for (let i = 0; i < NUM_DATASET_ELEMENTS / chunkSize; i++) {
const datasetBytesView = new Float32Array(
datasetBytesBuffer, i * IMAGE_SIZE * chunkSize * 4,
IMAGE_SIZE * chunkSize);
ctx.drawImage(
img, 0, i * chunkSize, img.width, chunkSize, 0, 0, img.width,
chunkSize);
const imageData = ctx.getImageData(0, 0, canvas.width, canvas.height);
for (let j = 0; j < imageData.data.length / 4; j++) {
// All channels hold an equal value since the image is grayscale, so// just read the red channel.datasetBytesView[j] = imageData.data[j * 4] / 255;
}
}
this.datasetImages = new Float32Array(datasetBytesBuffer);
resolve();
};
img.src = MNIST_IMAGES_SPRITE_PATH;
});
const labelsRequest = fetch(MNIST_LABELS_PATH);
const [imgResponse, labelsResponse] =
await Promise.all([imgRequest, labelsRequest]);
this.datasetLabels = new Uint8Array(await labelsResponse.arrayBuffer());
// Create shuffled indices into the train/test set for when we select a// random dataset element for training / validation.this.trainIndices = tf.util.createShuffledIndices(NUM_TRAIN_ELEMENTS);
this.testIndices = tf.util.createShuffledIndices(NUM_TEST_ELEMENTS);
// Slice the the images and labels into train and test sets.this.trainImages =
this.datasetImages.slice(0, IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
this.testImages = this.datasetImages.slice(IMAGE_SIZE * NUM_TRAIN_ELEMENTS);
this.trainLabels =
this.datasetLabels.slice(0, NUM_CLASSES * NUM_TRAIN_ELEMENTS);
this.testLabels =
this.datasetLabels.slice(NUM_CLASSES * NUM_TRAIN_ELEMENTS);
}
nextTrainBatch(batchSize) {
return this.nextBatch(
batchSize, [this.trainImages, this.trainLabels], () => {
this.shuffledTrainIndex =
(this.shuffledTrainIndex + 1) % this.trainIndices.length;
return this.trainIndices[this.shuffledTrainIndex];
});
}
nextTestBatch(batchSize) {
return this.nextBatch(batchSize, [this.testImages, this.testLabels], () => {
this.shuffledTestIndex =
(this.shuffledTestIndex + 1) % this.testIndices.length;
return this.testIndices[this.shuffledTestIndex];
});
}
nextBatch(batchSize, data, index) {
const batchImagesArray = new Float32Array(batchSize * IMAGE_SIZE);
const batchLabelsArray = new Uint8Array(batchSize * NUM_CLASSES);
for (let i = 0; i < batchSize; i++) {
const idx = index();
const image =
data[0].slice(idx * IMAGE_SIZE, idx * IMAGE_SIZE + IMAGE_SIZE);
batchImagesArray.set(image, i * IMAGE_SIZE);
const label =
data[1].slice(idx * NUM_CLASSES, idx * NUM_CLASSES + NUM_CLASSES);
batchLabelsArray.set(label, i * NUM_CLASSES);
}
const xs = tf.tensor2d(batchImagesArray, [batchSize, IMAGE_SIZE]);
const labels = tf.tensor2d(batchLabelsArray, [batchSize, NUM_CLASSES]);
return {xs, labels};
}
} // 我们直接使用mnist数据集这个经典的手写数字数据集,节约了收集手写数字的独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識集的时间
import {MnistData} from './data.js';
let cnnModel=null;
async function run() {
// 加载数据集 const data = new MnistData();
await data.load();
// 构造模型,设置模型参数 cnnModel = getModel();
// 训练模型 await train(cnnModel, data);
}
function getModel() {
const model = tf.sequential();
const IMAGE_WIDTH = 28;
const IMAGE_HEIGHT = 28;
const IMAGE_CHANNELS = 1;
// 在第一层,指定输入数据的形状,设置卷积参数 model.add(tf.layers.conv2d({
// 流入模型第一层的数据的形状。在本例中,我们的 MNIST 示例是 28x28 像素的黑白独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識。独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識数据的规范格式为 [row, column, depth] inputShape: [IMAGE_WIDTH, IMAGE_HEIGHT, IMAGE_CHANNELS],
// 要应用于输入数据的滑动卷积过滤器窗口的尺寸。在此示例中,我们将kernelSize设置成5,也就是指定 5x5 的卷积窗口。 kernelSize: 5,
// 尺寸为 kernelSize 的过滤器窗口数量 filters: 8,
// 滑动窗口的步长,即每次移动独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識时过滤器都会移动多少像素。我们指定步长为 1,表示过滤器将以 1 像素为步长在独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識上滑动。 strides: 1,
// 卷积完成后应用于数据的激活函数。在本例中,我们将应用修正线性单元 (ReLU) 函数,这是机器学习模型中非常常见的激活函数。 activation: 'relu',
// 通常使用 VarianceScaling作为随机初始化模型权重的方法 kernelInitializer: 'varianceScaling'
}));
// MaxPooling最大池化层使用区域最大值而不是平均值进行降采样 model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));
// 重复一遍conv2d + maxPooling // 注意这次卷积的过滤器窗口数量更多 model.add(tf.layers.conv2d({
kernelSize: 5,
filters: 16,
strides: 1,
activation: 'relu',
kernelInitializer: 'varianceScaling'
}));
model.add(tf.layers.maxPooling2d({poolSize: [2, 2], strides: [2, 2]}));
// 现在我们将2维滤波器的输出展平为1维向量,作为最后一层的输入。这是将高维数据输入给最后的分类输出层时的常见做法。 // 独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識是高维数据,而卷积运算往往会增大传入其中的数据的大小。在将数据传递到最终分类层之前,我们需要将数据展平为一个长数组。密集层(我们会用作最终层)只需要采用 tensor1d,因而此步骤在许多分类任务中很常见。 // 注意:展平层中没有权重。它只是将其输入展开为一个长数组。 model.add(tf.layers.flatten());
// 计算我们的最终概率分布,我们将使用密集层计算10个可能的类的概率分布,其中得分最高的类将是预测的数字。 const NUM_OUTPUT_CLASSES = 10;
model.add(tf.layers.dense({
units: NUM_OUTPUT_CLASSES,
kernelInitializer: 'varianceScaling',
activation: 'softmax'
}));
// 模型编译,选择优化器,损失函数categoricalCrossentropy,和精度指标accuracy(正确预测在所有预测中所占的百分比),然后编译并返回模型 const optimizer = tf.train.adam();
model.compile({
optimizer: optimizer,
loss: 'categoricalCrossentropy',
metrics: ['accuracy'],
});
return model;
}
// 我们的目标是训练一个模型,该模型会获取一张独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識,然后学习预测独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識可能所属的 10 个类中每个类的得分(数字 0-9)。 async function train(model, data) {
const metrics = ['loss', 'val_loss', 'acc', 'val_acc'];
const container = {
name: 'Model Training', tab: 'Model', styles: { height: '1000px' }
};
const fitCallbacks = tfvis.show.fitCallbacks(container, metrics);
const BATCH_SIZE = 512;
const TRAIN_DATA_SIZE = 5500;
const TEST_DATA_SIZE = 1000;
const [trainXs, trainYs] = tf.tidy(() => {
const d = data.nextTrainBatch(TRAIN_DATA_SIZE);
return [
d.xs.reshape([TRAIN_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
const [testXs, testYs] = tf.tidy(() => {
const d = data.nextTestBatch(TEST_DATA_SIZE);
return [
d.xs.reshape([TEST_DATA_SIZE, 28, 28, 1]),
d.labels
];
});
// 设置特征和标签 return model.fit(trainXs, trainYs, {
batchSize: BATCH_SIZE,
validationData: [testXs, testYs],
epochs: 10, //训练轮次 shuffle: true,
callbacks: fitCallbacks
});
} // 预测canvas上画的图形属于哪个分类 function predict(){
const input = tf.tidy(() => {
return tf.image
.resizeBilinear(tf.browser.fromPixels(canvas), [28, 28], true)
.slice([0, 0, 0], [28, 28, 1])
.toFloat()
.div(255)
.reshape([1, 28, 28, 1]);
});
const pred = cnnModel.predict(input).argMax(1);
console.log('预测结果为', pred.dataSync())
alert(`预测结果为 ${pred.dataSync()[0]}`);
};
document.getElementById('predict-btn').addEventListener('click', predict)
document.getElementById('clear-btn').addEventListener('click', clear)
document.addEventListener('DOMContentLoaded', run);
const canvas = document.querySelector('canvas');
canvas.addEventListener('mousemove', (e) => {
if (e.buttons === 1) {
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(255,255,255)';
ctx.fillRect(e.offsetX, e.offsetY, 10, 10);
}
});
function clear(){
const ctx = canvas.getContext('2d');
ctx.fillStyle = 'rgb(0,0,0)';
ctx.fillRect(0, 0, 300, 300);
};
clear();このプログラムの利点は、関連するデータがトレーニング セットが大きいほど、予測効果が高くなります。デメリットも明らかで、学習データセットや検証データセットの構築に膨大な作業がかかること、ブラウザを起動したまま学習を行うことも可能ですが、やはり時間がかかることが挙げられます。要約すると、このソリューションはいくつかの事前定義されたジェスチャを検出できますが、複数のユーザー ジェスチャ入力を通じてユーザーの特定のジェスチャを認識できるモデルをトレーニングするのは困難です。
手書き認識の OCR メソッドを使用して、ユーザー定義のジェスチャを認識できますか?
ユーザー入力は不確実であるため、ユーザーが入力したジェスチャは、事前に定義された特定のカテゴリに必ずしも対応するとは限りません。画像分類は「その他の」カテゴリを決定できますか?
tensorflow モデルの形式はフレームワーク言語に関連していますか?たとえば、Python でトレーニングされたモデルは tensorflow.js でも使用できますか?
マウスのインタラクションから得られるのが軌跡情報であり、この軌跡情報を通じて位置、形状、形状などを抽出することができます。より具体的な情報をお待ちください。したがって、マウスの時空間軌跡を記録し、ルールを使用してジェスチャ パスの特徴を要約し、高い確率でジェスチャを一意に識別できるパターンに固めて、それらの間の類似性を比較することができます。ジェスチャーパターンと通常のジェスチャー。パス データ構造を定義するときは、サイズやわずかな変形の影響を避けることを考慮する必要があることに注意してください。
まず、ユーザーが描いたジェスチャ パスを表現する必要があります。同じ形状で異なるサイズを持つオブジェクトは同じジェスチャと見なされるべきであるという基本原則を明確にします。ジェスチャ パスは、一連の単位ベクトルで表す必要があります。 Stroke では、ジェスチャ グラフィックを 128 個のベクトルに分割し、各ベクトルを単位ベクトルに変換します。このように、ジェスチャパスのサイズや長さが異なっていても、構造が同じであれば、それらを表すデータは同じになります。これにより、パスの大きさや微妙な変形による判定結果への影響が排除されます。
次に、測定されたパスの類似度を、測定されたベクトルデータの類似度に変換します。パス間の類似度は幾何学的量の特定の値によって決まるため、ベクトル類似度を計算する古典的な方法からコサイン類似度を求めました。
向量的相似度通常使用余弦相似度来度量,即计算向量夹角的余弦值。将两组数据两两对应,分成128组向量,每组2个,计算每组向量的余弦值并累加。最终得到的结果应该会在 [-128, 128] 之间,数值越大也就表示相似度越高。我们只需设置一个阈值,超过这个阈值的就认为匹配成功。
为了计算两个向量夹角的余弦值,引入向量的点乘,根据向量点乘公式(推导过程[3]):

这里|a|表示向量a的模(长度),θ表示两个向量之间的夹角。
两个互相垂直的向量的点积总是零。若向量a和b都是单位向量(长度为1),它们的点积就是它们的夹角的余弦。那么,给定两个向量,它们之间的夹角可以通过下列公式得到:

这个运算可以简单地理解为:在点积运算中,第一个向量投影到第二个向量上(这里,向量的顺序是不重要的,点积运算是可交换的),然后通过除以它们的标量长度来“标准化”。这样,这个分数一定是小于等于1的,可以简单地转化成一个角度值。
对于二维向量,我们用一个[number, number]元组来表示。
核心实现逻辑:
import { useEffect, useState, useRef, useMemo } from 'react'
import throttle from "lodash/throttle"
type Position = {x:number, y:number};
type Vector = [number, number];
// 预先定义特殊V字型的手势路径,便于调试。 const shapeVectors_v: Vector[] = [[5,16],[13,29],[4,9],[6,9],[8,8],[1,0],[1,0],[1,-2],[0,-3],[7,-11],[21,-34],[10,-19]];
const shapeVectors_l: Vector[] = [[0,15],[0,33],[0,19],[0,4],[0,3],[0,8],[2,6],[11,0],[28,0],[18,0],[5,0],[1,0]]
const shapeVectors_6: Vector[] = [[-41,18],[-40,33],[-30,39],[-24,62],[1,53],[40,27],[38,2],[30,-34],[7,-41],[-31,-21],[-38,-4],[-19,0]];
const shapeVectors: {[key:string]: Vector[]} = {
v: shapeVectors_v,
l: shapeVectors_l,
6: shapeVectors_6
}
function Gesture(){
const pointsRef = useRef<Position[]>([]);
const sparsedPointsRef = useRef<Position[]>([]);
const vectorsRef = useRef<Vector[]>([]);
const canvasContextRef = useRef<CanvasRenderingContext2D>()
const containerRef = useRef<HTMLDivElement>(null)
const [predictResults, setPredictResults] = useState<{label: string, similarity: number}[]>([])
// 按一定的时间间隔采集点 const handleMouseMoveThrottled = useMemo(()=>{return throttle(handleMouseMove, 16)}, [canvasContextRef.current])
useEffect(()=>{
const canvasEle = document.getElementById('canvas-ele') as HTMLCanvasElement;
const ctx = canvasEle.getContext('2d')!;
canvasContextRef.current=ctx;
handleClear();
}, [])
function handleMouseDown(){
containerRef?.current?.addEventListener('mousemove', handleMouseMoveThrottled);
}
function handleMouseUp(){
console.log('up')
containerRef?.current?.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
pointsRef.current=[]
}
// 为了方便示意,我们把鼠标路径可视化出来。 function drawPoint(x:number,y:number){
// console.log(x, y) // canvasContext?.arc(x, y, 5, 0, Math.PI*2); (canvasContextRef.current!).fillStyle = 'red';
canvasContextRef.current?.fillRect(x, y, 10,10)
}
// 鼠标滑过时,记录下一串间隔的点。 function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
drawPoint(x, y)
const newPoints = [...pointsRef.current, {x,y}];
pointsRef.current = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPointsRef.current=sparsedNewPoints;
const vectors = points2Vectors(sparsedNewPoints)
vectorsRef.current = vectors;
console.log('points', x, y)
// const angles = vectors.map(vector2PolarAngle) // console.log('angles', angles[angles.length-1]) }
// 如果点太多,处理起来性能不佳,除了节流之外,我们始终将点抽稀到13个(我们假设每个手势的持续时间都不低于200ms,能保证在节流16ms的情况下,至少收集到13个原始点,这样抽稀才有意义) // 抽稀的策略是以固定的间隔平均抽,这样有个潜在问题:如果用户划手势时速度不够均匀,比如在同一个手势路径中某段时间划的速度比较快(点会比较密集),在某段时间的速度比较慢(点会比较稀疏),那由抽稀后的点构造出的路径向量就会比较失真,影响最终判断的准确性。 // 优化的方案是在空间上采用分区抽稀的策略,避免用户手速不均匀导致的问题,但分区逻辑比较复杂,我们暂且按下不做深入研究。 // todo: 抽稀后,相邻的点不能重复,否则会有0向量、对运算和判断造成干扰。 function sparsePoints(points: Position[]){
const sparsedLength = 13;
if(points.length<=sparsedLength){
return points;
}else{
let sparsedPoints = [];
let step = points.length/sparsedLength;
for(let i=0; i<sparsedLength; i++){
const curIndex = Math.round(step*i);
sparsedPoints.push(points[curIndex])
}
return sparsedPoints;
}
}
// 对于非闭合的路径,手势方向会影响判断逻辑,相同的路径可能是由相反的手势方向画出来的。比如L形的手势。 // 对于闭合的路径,手势的方向和起止位置都会影响判断逻辑,相同的路径可能是由相反的手势方向画出来的,也可能是由不同起始位置画出来的。比如圆形的手势。 // 为了消除相同路径不同画法的影响,我们做如下处理
function normalizePoints(points:Position[]){
// if (是闭合路径) 将位置在最左上角的点作为数组的第一位,其余的依次排列,然后返回 // else 原样返回 return points;
}
// 相邻的两个点相连,生成一个向量。用这n个点的坐标生成n-1个向量,这n-1个向量组成一段路径,用来表示一个鼠标手势。 function points2Vectors(points: Position[]){
if(points.length<=1){
return []
}else{
return points.reduce((pre:Vector[], cur, curIdx)=>{
if(curIdx===0){return []}
const prePoint = points[curIdx-1];
const vec:Vector = [cur.x-prePoint.x, cur.y-prePoint.y];
return [...pre, vec];
}, [])
}
}
// 判断两条路径是否是相同,保证组成两条路径的向量数相同,然后计算两条路径对应向量的余弦相似度(取值在-1~1之间,越接近-1或者1,越相似)。最后再与定义的阈值比较,超过阈值就认为路径相同。 function judge(vec1:Vector[], vec2: Vector[], threshold?:number){
// 暂定阈值为0.5 const finalThreshold = threshold||0.5;
// 为消除路径方向的影响(一个向量与另一个反向相反的向量的余弦值是-1,应该认为它们形状相同),反转路径后再次判断 return cosineSimilarity(vec1, vec2)>=finalThreshold || cosineSimilarity(vec1, vec2.reverse())>=finalThreshold
}
// 两组向量的余弦相似度,保证组成两条路径的向量数相同,然后计算两条路径对应向量的余弦值,累加取均值.取值在-1~1之间,越接近-1或者1,越相似. function cosineSimilarity(vec1: Vector[], vec2: Vector[]){
if(vec1.length!==vec2.length){
console.warn('进行比较的两个路径长度(路径内的向量数)必须一致')
return 0;
}else{
let cosValueSum = 0;
vec1.forEach((v1, i)=>{
cosValueSum+=vectorsCos(v1, vec2[i])
})
// 取余弦值的绝对值,绝对值越接近1,相似度越高。 const cosValueRate = Math.abs(cosValueSum/vec1.length);
console.log('cosValueRate', cosValueRate)
return cosValueRate;
}
}
// 两个向量的余弦值 function vectorsCos(v1:Vector, v2:Vector){
// 特殊情况,0向量的余弦值我们认为是1 if(vectorLength(v1)*vectorLength(v2)===0){
return 1;
}
return vectorsDotProduct(v1, v2)/(vectorLength(v1)*vectorLength(v2));
}
// 向量的点乘 function vectorsDotProduct(v1:Vector, v2:Vector){
return v1[0]*v2[0]+v1[1]*v2[1];
}
// 向量的长度 function vectorLength(v:Vector){
return Math.sqrt(Math.pow(v[0], 2)+Math.pow(v[1], 2))
}
// 向量归一化,消除向量在长度上的差异,控制变量,方便训练机器学习模型(https://zhuanlan.zhihu.com/p/424518359) function normalizeVector(vec:Vector){
const length = Math.sqrt(Math.pow(vec[0],2)+Math.pow(vec[1], 2))
return [vec[0]/length, vec[1]/length]
}
function handlePredict(){
const results = Object.keys(shapeVectors).map(key=>({
label: key,
similarity: cosineSimilarity(shapeVectors[key], vectorsRef.current),
}))
setPredictResults(results);
console.log('results', results)
}
function handleClear(){
pointsRef.current=[];
sparsedPointsRef.current=[];
vectorsRef.current=[];
(canvasContextRef.current!).fillStyle = 'rgb(0,0,0)';
(canvasContextRef.current!).fillRect(0, 0, 500, 500);
setPredictResults([]);
}
// 工程化封装,为某个dom元素增加自定义手势事件 function addCustomEvent(ele: HTMLElement, eventName: string, eventLisener:(...args:any[])=>any){
let points = [], sparsedPoints=[],vecs:Vector[]=[];
const customEvent = new Event(eventName);
function handleMouseMove(e: any){
const x:number = e.offsetX, y:number = e.offsetY;
const newPoints = [...pointsRef.current, {x,y}];
points = newPoints;
const sparsedNewPoints = sparsePoints(newPoints);
sparsedPoints=sparsedNewPoints;
const newVectors = points2Vectors(sparsedNewPoints)
vecs = newVectors;
console.log('points', x, y)
}
const handleMouseMoveThrottled = throttle(handleMouseMove, 16)
function handleMouseDown(){
ele.addEventListener('mousemove', handleMouseMoveThrottled);
}
function handleMouseUp(){
console.log('up')
ele.removeEventListener('mousemove', handleMouseMoveThrottled);
console.log('points', sparsedPointsRef.current)
console.log('vectors', JSON.stringify(vectorsRef.current))
if(judge(vecs, shapeVectors['l'], 0.6)){
ele.dispatchEvent(customEvent)
}
points=[], sparsedPoints=[], vecs=[];
}
ele.addEventListener(eventName, eventLisener)
ele.addEventListener('mousedown', handleMouseDown);
ele.addEventListener('mouseup', handleMouseUp);
return function distroyEventListener(){
ele.removeEventListener(eventName, eventLisener)
}
}
return
<canvas width='500' height="500"></canvas>
<section>
<button notallow={handlePredict}>预测</button>
<button notallow={handleClear}>清空</button>
</section>
<ul>
{predictResults.map(e=>(
<li key={e.label}>
{`与 ${e.label}的相似度:${e.similarity}`}
</li>
))}
</ul>
}
export default Gesture点和向量的计算属于计算密集型任务,且其需要与主线程通信的数据量不大,考虑将其搬进webworker。此外,canvas的渲染性能也可以使用requestAnimationFrame和硬件加速来优化。属于常见的工程层面优化,此处略。
余弦相似度的方法,优势在于计算量不大,可以在运行时由用户自定义手势,且所需保存的数据量不大,也适合网络传输。劣势在于难以衡量复杂多笔画、没有严格笔顺的图形的相似度。
针对二维平面内的手势识别方案如何扩展到三维空间呢?比如在VR/MR场景内,手势路径会是一组三维向量,如果我们能将余弦相似度的适用范围扩展到三维向量,也就顺理成章地解决了这个问题。
基本思路就是分别分析两个三维向量在xoy平面上的投影之间的夹角以及在yoz平面上的投影之间的夹角的余弦相似度,将两者的乘积作为两个三维向量之间的余弦相似度。判断逻辑与二维向量的一致。
综合考虑机器学习的方案和几何分析方案的优劣势,我们做如下设计。对于预设的手势,我们构造数据集、离线训练模型,然后将模型内置在产品内。对于自定义的手势,我们采用几何分析方案,让用户连续输入3次,先计算每次输入的路径的两两之间的相似度,且选出相似度的最小值n,如果最小值n大于某个阈值m,且每次输入的路径与其他已有路径的相似度均小于m时,我们就将距离其余两条路径的相似度之和最小的那条路径作为用户自定义的新路径,n作为其相似度判断的阈值。
参考资料
[1]预训练好的模型: https://github.com/tensorflow/tfjs-models
[2]环境搭建: https://github.com/tensorflow/tfjs#getting-started
[3]推导过程: https://blog.csdn.net/dcrmg/article/details/52416832
[4]复杂鼠标手势的识别是如何实现的? - 知乎: https://www.zhihu.com/question/20607813
[5]点积相似度、余弦相似度、欧几里得相似度: https://zhuanlan.zhihu.com/p/159244903
[6]机器学习并没有那么深奥,它还很有趣(1)-36氪: https://m.36kr.com/p/1721248956417
[7]计算向量间相似度的常用方法: https://cloud.tencent.com/developer/article/1668762
[8]C#手势库的核心逻辑实现: https://github.com/poerin/Stroke/blob/master/Stroke/Gesture.cs
[9]什么是张量 (tensor)? - 知乎: https://www.zhihu.com/question/20695804
[10]使用 CNN 识别手写数字: https://codelabs.developers.google.com/codelabs/tfjs-training-classfication?hl=zh-cn#0
[11]机器学习: https://zh.m.wikipedia.org/zh/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0
[12]文字识别方法整理(2015~2019): https://zhuanlan.zhihu.com/p/65707543
以上が独自のインタラクティブなイベントを作成 - 画面ジェスチャー認識の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。