
最近、「羊」という話題がネット上で話題になっていて、2級の難易度や合格方法についての記事が増えていますが、ゲームの難易度については以下のような記事で議論されています。計算量の視点. まだ記事が存在していないかもしれないので、今回は試しに計算量についても記事を書いてみます。
ゲームの仕組みは比較的シンプルで、簡単に言うと、マップ上にいくつかの種類のブロックがあり、プレイヤーはブロックを選択して自分のスロットに入れることができます(スロットには上部があります)制限は定数です)、スロットに同じ種類のブロックが 3 つある場合、それらは削除されます。ゲームの目標は、すべてのブロックを削除することです。ゲームの難しさは、マップ上のブロックが積み重なっていることです。下に積み上げられたブロックは選択できません。上のブロックがスロットに置かれた後でのみ選択できます (つまり、ロックが解除されます)。場合によっては、下に積み上げられたブロックが隠蔽されているため種類は不明。
実際、羊の羊のメカニズムはいくつかのミニゲームのメカニズムと非常によく似ており、これらのミニゲームの多くは NP 完全であることが証明されています。私たちは、羊を飼うことが NP 完全であるという昇進も証明できると比較的自信を持っています。ここでは、促進された羊同士のゲームが NP 完全であることを示すために、比較的弱く単純な還元構造を示します。ここで話している一般化は、ブロック タイプの数が定数に限定されず、ブロックされたブロック タイプが決定されて既知であり、スロットの数が 3 に固定されていることを意味します (スロットの数が 3 であれば同様の方法を使用できます)。スロットは他の定数です, ゲームの開始時に, プレーヤーは特別なタイプのブロックを取ることを強制されます, ゲームの終了時にのみ削除できます. 全プロセス中, このブロックはスロットを占有します,これはスロットが欠落していることに相当します)。もちろん、ここではゲームの小道具の影響は考慮しません。
この記事の削減は主に、ゲームとパズルの計算の複雑さの Web ページから盗用したものであり、麻雀ゲーム (連聯館に似たゲーム、地域によっては麻雀とも呼ばれる) が、 ) は NP 完全還元です。
我々は依然として 3-SAT の古典的な NP 完全問題をリダクション問題として使用しています。 3-SAT 式の変数ごとに 3 つの正方形の山を設定します。1 つの正方形の山は変数 (TRUE または FALSE) の割り当てをシミュレートするために使用され、1 つの正方形の山は FALSE の割り当てに対応し、1 つの正方形の山は変数の割り当てに対応します。 TRUE の割り当て。シミュレートされた変数の代入ブロックのスタックには 2 つのレベルがあります。最初のレベルには、変数に対応する 4 つの同一のブロックが含まれます。2 番目のレベルには、それぞれ TRUE と FALSE に割り当てられた変数を含む 1 つのブロックと充填ブロックが含まれます。 FALSE に割り当てられた値に対応するブロックのヒープは通常多層です (1 層に減らすこともできます)。最上位層には、FALSE に割り当てられた変数に対応する 2 つのブロックが含まれます (以前に割り当てられたブロック ヒープで使用するため)。下層には、FALSE に割り当てられた変数に対応するブロック、節マス (変数が出現しない節に対応)、およびフィラーマスが含まれます。 TRUE が割り当てられたブロック ヒープに対応する構造も同様です。最後に、解を検証するためのブロックの山ですが、この山は多層構造になっており、上が文節に対応するブロック、真ん中が変数に対応するブロック、下が文節に対応するブロックとなっています。
3-SAT のインスタンスが 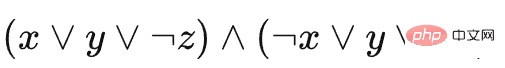 であると仮定して、この削減を説明するために特定の例を使用します。それでは、羊作りゲームの例は以下の通りです(各ブロックの種類や積み方を表現するため、横から見た図で表示しています)
であると仮定して、この削減を説明するために特定の例を使用します。それでは、羊作りゲームの例は以下の通りです(各ブロックの種類や積み方を表現するため、横から見た図で表示しています)
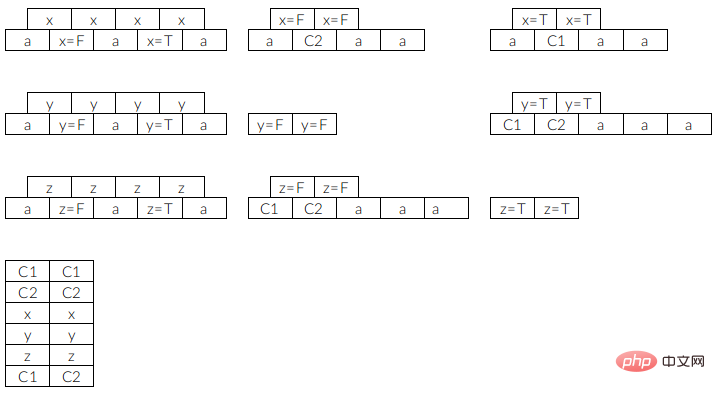
このうち、C1 は 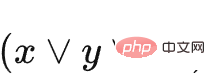 を表し、C2 は
を表し、C2 は 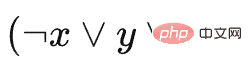 を表し、a は塗りつぶし四角形であり、四角形 a は四角形を抑制しません。 , そのため、最後まで残してすべて削除することができます。他のブロックには影響しません。ここで設定したスロットの数は 3 であることに注意してください。これは、特定のブロックを選択してスロットに配置した後、このタイプのブロックを削除する必要があることを意味します。削除しないと、ゲームは続行されません。
を表し、a は塗りつぶし四角形であり、四角形 a は四角形を抑制しません。 , そのため、最後まで残してすべて削除することができます。他のブロックには影響しません。ここで設定したスロットの数は 3 であることに注意してください。これは、特定のブロックを選択してスロットに配置した後、このタイプのブロックを削除する必要があることを意味します。削除しないと、ゲームは続行されません。
式が満たされる場合、満たされたときの各変数の割り当てに従ってブロックを削除できます。たとえば、xyz がすべて FALSE に割り当てられていると仮定すると、左端の 3 つの x、y、z が削除されます。このようにして、2 番目の層の正方形 x=F、y=F、および z=F のロックが解除されます。すべての x=F y=F z=F ブロック、その後 1 つの C1 ブロックと 2 つの C2 ブロックのロックが解除され、一番下の検証ブロックの山を使用して、検証パイルの上位 2 つの層を削除できます。 , すると、真ん中の変数xyzブロックもロックが解除され、すぐに削除することができ、最終的には制限がなく、すべてのブロックを削除することができます。
逆に、すべてのブロックを取り除くことができれば (つまり、レベルを通過できれば)、式は満たされます。検証ヒープ内の変数 xyz ブロックを削除したい場合は、上位の C1 C2 句ブロックを最初に削除する必要があり、句ブロックは代入ブロックに限定され、代入ブロックは変数ブロックに限定され、変数ブロックの配置 配置方法は、変数に値を割り当てるときに、各変数を FALSE または TRUE のいずれか 1 つにのみ割り当てることができることを決定します (具体的には、ゲーム開始時に 4 つの x マスのうち 3 つを任意に削除した後、正方形 x=F および x=T ロックが解除されていないものが存在する必要があります)。これは、ブロックが削除される順序が式を満たす割り当てを意味することを意味します。
これは、3-SAT 式が満たせる必要十分条件は、対応する羊の羊ゲーム インスタンスを通過できることであることを意味します。そして、羊の中の羊は明らかに NP に属します。演算シーケンスがすべてのブロックを除去できるかどうかは多項式時間で決定できるため、次の命題を証明しました。 all ブロックされたブロックの種類が確実で既知であるという条件の下で、昇格された羊-le-羊ゲームは NP 完全です。
人間以外の言葉で言うと、P が存在しない限り、一般化された羊間のレベルに解があるかどうかを判断する多項式時間計算量のアルゴリズムを設計する方法はありません。 =NP (この 4 文字の方程式は、土地の賞金と 100 万ドルの価値があるため、座って証明または反証しようとしないでください)。人間の言葉で言えば、たとえブロックされたブロックの種類が確実でわかっていたとしても、コンピューターは羊がそのレベルを通過できるかどうかを迅速に判断することが(ほとんど)できません。
以上がNPは完全に羊を割って羊を失いましたか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。