過去 10 年間で論文数が急増していますが、ディープラーニングはどのようにして数学的推論への扉をゆっくりと開いていくのでしょうか?
数学的推論は人間の知性の重要な現れであり、数値データと言語に基づいて理解し、意思決定を行うことを可能にします。数的推論は、科学、工学、金融、日常生活などのさまざまな分野に適用され、パターン認識や数値計算などの基本的なスキルから、問題解決、論理的推論、抽象的思考などの高度なスキルまで、幅広い能力を網羅します。
数学の問題を解決し、数学の定理を証明できる AI システムの開発は、機械学習と自然言語処理の分野で長い間研究の焦点となってきました。これも1960年代に遡ります。
# ディープラーニングの台頭以来、過去 10 年間で、この分野に対する人々の関心は大幅に高まりました。
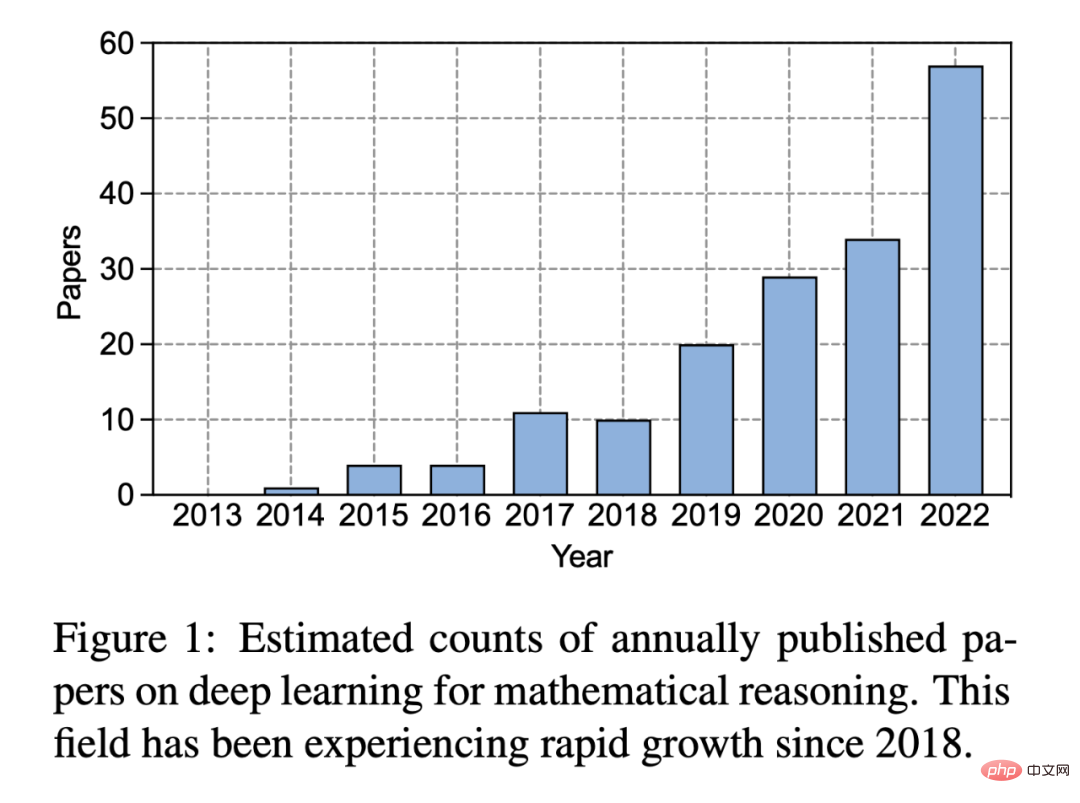
##図 1: 数学的推論に関して毎年出版される深層学習論文の推定数。 2018年以降、この地域は急速な成長を遂げています。
# ディープラーニングは、質問応答や機械翻訳など、さまざまな自然言語処理タスクで大きな成功を収めています。同様に、研究者は数学的推論のためのさまざまなニューラル ネットワーク手法を開発しており、文章問題、定理証明、幾何学的問題の解決などの複雑なタスクを処理するのに効果的であることが証明されています。たとえば、深層学習ベースのアプリケーション問題ソルバーは、シーケンスツーシーケンスのフレームワークを採用し、数式を生成するための中間ステップとしてアテンション メカニズムを使用します。さらに、大規模なコーパス モデルと Transformer モデルを使用すると、事前トレーニングされた言語モデルがさまざまな数学的タスクで有望な結果を達成しました。最近、GPT-3 のような大規模な言語モデルは、複雑な推論と文脈学習において優れた能力を実証することにより、数学的推論の分野をさらに進歩させました。
最近発表されたレポートでは、UCLA およびその他の機関の研究者が数学的推論における深層学習の進歩を体系的にレビューしました。

紙のリンク: https://arxiv.org/pdf/2212.10535.pdf
#プロジェクト アドレス: https://github.com/lupantech/dl4math具体的には、この記事ではさまざまなタスクとデータセットについて説明します (セクション 2) 、数学におけるニューラル ネットワーク (セクション 3) と事前学習済み言語モデル (セクション 4) の進歩を検証します。数学的推論における大規模言語モデルの文脈学習の急速な発展も調査されています (セクション 5)。この記事では、既存のベンチマークをさらに分析し、マルチモーダル環境や低リソース環境にはあまり注目が払われていないことがわかりました (セクション 6.1)。証拠に基づいた研究は、現在のコンピューティング能力の表現が不十分であり、深層学習手法が数学的推論に関して一貫性がないことを示しています (セクション 6.2)。その後、著者らは、一般化と堅牢性、信頼できる推論、フィードバックからの学習、およびマルチモーダルな数学的推論の観点から、現在の研究の改善を提案しています (セクション 7)。
タスクとデータセット
このセクションでは、深層学習手法を使用した数学的推論の研究に現在利用できるさまざまなタスクとデータセットを検討します。表 2 を参照してください。
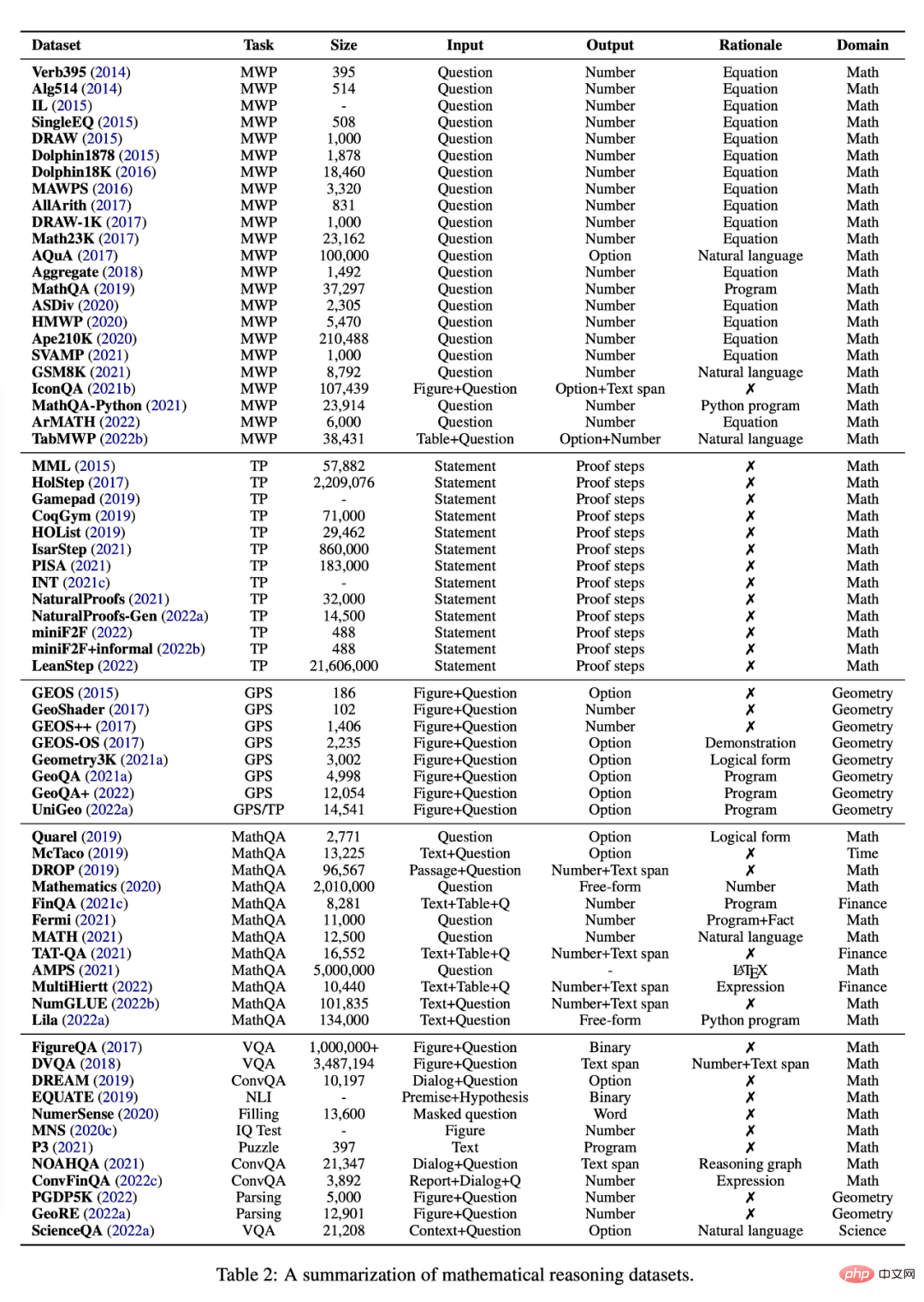
数学の文章問題には短い A が含まれています人々、実体、数量が関与する物語。それらの数学的関係は、一連の方程式によってモデル化でき、その解によって問題の最終的な答えが明らかになります。表 1 は代表的な例です。問題には、加算、減算、乗算、除算の 4 つの基本的な数学演算が 1 つまたは複数のステップで含まれます。 NLP システムへの応用問題の課題は、言語理解、意味分析、およびさまざまな数学的推論能力の需要にあります。
既存の文章題データセットは、オンライン学習 Web サイトから収集したり、教科書から収集したり、人間が手動で注釈を付けたりした小学校レベルの問題をカバーしています。初期の文章問題のデータ セットは比較的小さいか、少数のステップに限定されていました。最近のデータセットの中には、問題の多様性と難易度を高めることを目的としたものもあります。たとえば、現在最大の公開問題セットである Ape210K は、210,000 個の小学校の文章問題で構成されていますが、GSM8K の問題には最大 8 ステップの解決策が含まれています。 SVAMP は、単純なバリエーションの文章問題に対する深層学習モデルの堅牢性をテストするベンチマークです。最近確立されたデータセットの中には、テキスト以外のモダリティを含むものもあります。たとえば、IconQA は視覚的な背景として抽象的な図を提供し、TabMWP は各質問に表形式の背景を提供します。
ほとんどの文章題データ セットは、注釈付きの方程式が解として正当化される理由を提供します (表 1 を参照)。学習されたソルバーのパフォーマンスと解釈可能性を向上させるために、MathQA には正確な計算手順の注釈が付けられ、MathQA-Python は具体的な Python プロシージャを提供します。他のデータセットは、人間が読むのにより適していると考えられる複数のステップの自然言語ソリューションで質問に注釈を付けます。 Lila は、Python プログラミングの原理を使用して、前述の文章題データ セットの多くに注釈を付けました。
理論的証明
自動化された定理証明は、AI の分野における長期的な課題です。この問題には通常、一連の論理的議論を通じて数学の定理が真実であることを証明することが含まれます。定理の証明には、効率的な複数ステップの戦略の選択、背景知識の使用、算術や導出などの記号演算の実行など、さまざまなスキルが必要です。
最近、正式な対話型定理証明器 (ITP) での定理証明に言語モデルを使用することへの関心が高まっています。定理は ITP のプログラミング言語で記述され、既知の事実になるまで「証明ステップ」を生成することで簡略化されます。その結果、検証された証明を構成する一連のステップが得られます。
非公式定理証明は、定理証明の代替手段、つまり、自然言語と「標準」数学表記 (LATEX など) を組み合わせてステートメントと証明を記述することを提案します。人間によって正しいかどうかチェックされます。
新興の研究分野は、非公式の定理証明と形式的な定理証明の要素を組み合わせることを目的としています。たとえば、Wu et al. (2022b) は、非公式なステートメントを正式なステートメントに変換することを検討しており、Jiang et al. (2022b) は、miniF2F非公式と呼ばれる、非公式なステートメントと証明を追加した新しいバージョンの miniF2F ベンチマークをリリースしました。 Jiang et al. (2022b) は、提供された (または生成された) 非公式の証明を正式な証明に変換することを検討しています。
幾何問題
幾何問題の自動解決 (GPS) も、数学分野で長年使用されている人工知能です。推論研究の使命を担っており、近年広く注目を集めています。文章問題とは異なり、幾何学問題は自然言語によるテキスト記述と幾何学図形で構成されます。図 2 に示すように、マルチモーダル入力は幾何学的要素のエンティティ、プロパティ、および関係を記述しますが、その目的は未知の変数に対する数値解を見つけることです。 GPS は複雑なスキルが必要なため、ディープ ラーニング手法にとっては困難なタスクです。これには、マルチモーダルな情報を解析し、象徴的な抽象化を行い、定理の知識を利用し、定量的推論を行う能力が含まれます。
初期のデータ セットはこの分野の研究を促進しましたが、これらのデータ セットは比較的小さいか、一般に公開されていなかったため、深層学習手法の開発が制限されました。この制限に対処するために、Lu らは、マルチモーダル入力に対して統一された論理形式で注釈が付けられた 3002 個の多肢選択ジオメトリの質問で構成される Geometry3K データセットを作成しました。最近では、GeoQA、GeoQA、UniGeo などの大規模なデータセットが導入され、最終的な答えを得るためにニューラル ソルバーによって学習および実行できるプログラムで注釈が付けられています。
数学 Q&A
最近の研究では、SOTA 数学的推論システムは推論において「脆弱」である可能性があることが示されています。つまり、モデルは「満足のいく」パフォーマンスを達成するために、特定のデータセットからの誤った信号とプラグアンドプレイ計算に依存しています。この問題を解決するために、さまざまな側面から新しいベンチマークが提案されています。 Mathematics (Saxton et al., 2020) データセットには、算術、代数、確率、微積分にわたるさまざまなタイプの数学問題が含まれています。このデータセットは、モデルの代数一般化能力を測定できます。同様に、MATH (Hendrycks et al.、2021) は、複雑な状況におけるモデルの問題解決能力を測定するための、挑戦的な競争数学で構成されています。
一部の作業では、質問の入力にテーブルの背景を追加しました。たとえば、FinQA、TAT-QA、および MultiHiertt は、回答するために表の理解と数的推論を必要とする質問を収集します。いくつかの研究では、大規模な数値推論のための統一ベンチマークを提案しています。 NumGLUE (Mishra et al.、2022b) は、8 つの異なるタスクでモデルのパフォーマンスを評価することを目的としたマルチタスク ベンチマークです。 Mishra et al. 2022a は、広範囲の数学的トピック、言語の複雑さ、質問形式、および背景知識の要件に及ぶ 23 の数値推論タスクで構成される Lila を提案することで、この方向性をさらに推し進めました。
AI は他の種類の定量的問題でも成果を上げています。たとえば、数字、グラフ、図は、大量の情報を簡潔に伝えるために不可欠なメディアです。 FigureQA、DVQA、MNS、PGDP5K、GeoRE はすべて、グラフベースのエンティティ間の定量的な関係を推論するモデルの能力を研究するために導入されました。 NumerSense は、既存の事前トレーニング済み言語モデルが数値的な常識知識を感知できるかどうか、またどの程度まで感知できるかを調査します。 EQUATE は、量的推論のさまざまな側面を自然言語推論フレームワークで形式化します。定量的推論は、金融、科学、プログラミングなどの特定の分野でも頻繁に使用されます。たとえば、ConvFinQA は財務報告書に対して会話型の質疑応答の形式で数値推論を実行します。ScienceQA は科学分野での数値推論に関係し、P3 は深層学習モデルの関数推論能力を研究して、特定のプログラムが返す有効な入力を見つけます。真実。
数学的推論のためのニューラル ネットワーク
この記事の著者は、数学的推論に使用されるいくつかの一般的なニューラル ネットワークについても要約しています。
Seq2Seq Network
Seq2Seq ニューラル ネットワークは、アプリケーション問題や定理証明などの数学的推論タスクにうまく適用されています。 、幾何学の問題と数学の問題の答え。 Seq2Seq モデルは、通常、数学的推論をシーケンス生成タスクとして形式化するエンコーダー/デコーダー アーキテクチャを使用します。このメソッドの基本的な考え方は、入力シーケンス (数学の問題など) を出力シーケンス (方程式、プログラム、証明など) にマッピングすることです。一般的なエンコーダおよびデコーダには、長期短期記憶ネットワーク (LSTM) およびゲート反復ユニット (GRU) が含まれます。広範な研究により、Seq2Seq モデルは、双方向バリアントである BiLSTM や BiGRU を含む、以前の統計学習方法に比べてパフォーマンス上の利点があることが示されています。 DNS は、Seq2Seq モデルを使用して文章問題から数式に文章を変換した最初の作品です。
グラフベースのネットワーク
Seq2Seq メソッドには、手作業に依存せずに数式を生成できるという利点があります。細工された機能。数式は、式内の構造化情報を記述する抽象構文ツリー (AST) やグラフベースの構造などのツリーベースの構造に変換できます。ただし、この重要な情報は Seq2Seq アプローチでは明示的にモデル化されていません。この問題を解決するために、研究者は式の構造を明示的にモデル化するグラフベースのニューラル ネットワークを開発しました。
Sequence-to-tree (Seq2Tree) モデルは、出力シーケンスをエンコードするときにツリー構造を明示的にモデル化します。たとえば、Liu らは、方程式の AST 情報をより有効に活用するために Seq2Tree モデルを設計しました。対照的に、Seq2DAG は、グラフ デコーダが複数の変数間の複雑な関係を抽出できるため、方程式を生成するときにシーケンス グラフ (Seq2Graph) フレームワークを適用します。入力数学的シーケンスをエンコードするときに、グラフベースの情報を埋め込むこともできます。たとえば、ASTactic は AST に TreeLSTM を適用して、定理証明の入力目標と前提を表します。
アテンションベースのネットワーク
アテンション メカニズムは、デコード プロセス中に入力隠れベクトルを考慮に入れて、自然言語処理とコンピューター ビジョンの問題にうまく適用されています。研究者たちは、数学的概念間の最も重要な関係を特定するために使用できるため、数学的推論タスクにおけるその役割を研究してきました。たとえば、MATH-EN は、自己注意を通じて学習した長距離の依存関係情報を利用する文章問題ソルバーです。注意ベースの方法は、幾何学問題や定理証明など、他の数学的推論タスクにも適用されています。より良い表現を抽出するために、さまざまなマルチヘッド アテンションを使用してさまざまなタイプの MWP 特徴を抽出する Group-ATT や、知識認識情報の抽出に適用されるグラフ アテンションなど、さまざまなアテンション メカニズムが研究されています。
その他のニューラル ネットワーク
数学的推論タスクの深層学習手法では、次のような他のニューラル ネットワークも利用できます。畳み込みとして ニューラル ネットワークとマルチモーダル ネットワーク。一部の作品では、畳み込みニューラル ネットワーク アーキテクチャを使用して入力テキストをエンコードし、モデルに入力内のシンボル間の長期的な関係を捕捉する機能を与えています。たとえば、Irving et al. は、大規模理論における前提選択に畳み込みネットワークに依存する、定理証明におけるディープ ニューラル ネットワークの最初の応用を提案しました。
幾何学的な問題解決やグラフベースの数学的推論など、マルチモーダルな数学的推論タスクは、ビジュアル質問応答 (VQA) 質問として形式化されます。このドメインでは、ビジュアル入力は ResNet または Faster-RCNN を使用してエンコードされ、テキスト表現は GRU または LTSM を通じて取得されます。続いて、BAN、FiLM、DAFA などのマルチモーダル融合モデルを使用して関節表現を学習します。
他のディープ ニューラル ネットワーク構造も数学的推論に使用できます。 Zhang らは、空間推論におけるグラフ ニューラル ネットワーク (GNN) の成功を利用し、それを幾何学的問題に適用しました。 WaveNet は、縦方向の時系列データを解決できるため、定理証明に適用されます。さらに、Transformer は、DDT での数式の生成において GRU よりも優れていることがわかりました。また、MathDQN は、主にその強力な検索機能を活用して、数学的な文章題を解くための強化学習を探求した最初の作品です。
数学的推論のための事前トレーニング済み言語モデル
事前トレーニング済み言語モデルは、数学にも適用される幅広い NLP タスクで大幅なパフォーマンスの向上を示しています 関連する問題、以前の研究では、事前トレーニングされた言語モデルが文章問題を解決し、定理証明やその他の数学的タスクを支援する際にうまく機能することが示されています。ただし、これを数学的推論に使用すると、いくつかの課題が生じます。
まず第一に、事前トレーニング済み言語モデルは、数学的データに基づいて特別にトレーニングされていません。そのため、自然言語タスクよりも数学関連タスクの習熟度が低くなる可能性があります。また、大規模な事前トレーニングに利用できる数学的または科学的データは、テキスト データに比べて少ないです。
第 2 に、事前トレーニングされたモデルのサイズは増大し続けており、特定の下流タスクのためにモデル全体を最初からトレーニングするのはコストがかかります。
さらに、ダウンストリーム タスクは、構造化されたテーブルやグラフなど、さまざまな入力形式やモダリティを処理する場合があります。これらの課題に対処するには、研究者は事前トレーニングされたモデルを微調整するか、下流のタスクでニューラル アーキテクチャを調整する必要があります。
最後に、事前トレーニングされた言語モデルは大量の言語情報をエンコードできますが、言語モデリングの目標だけを見ると、モデルが数値表現や数値表現を学習するのは難しいかもしれません。高度な推理力。これを念頭に置いて、最近の研究では、基礎から始まるコースで数学関連のスキルを注入することが調査されています。
数学の自己教師あり学習
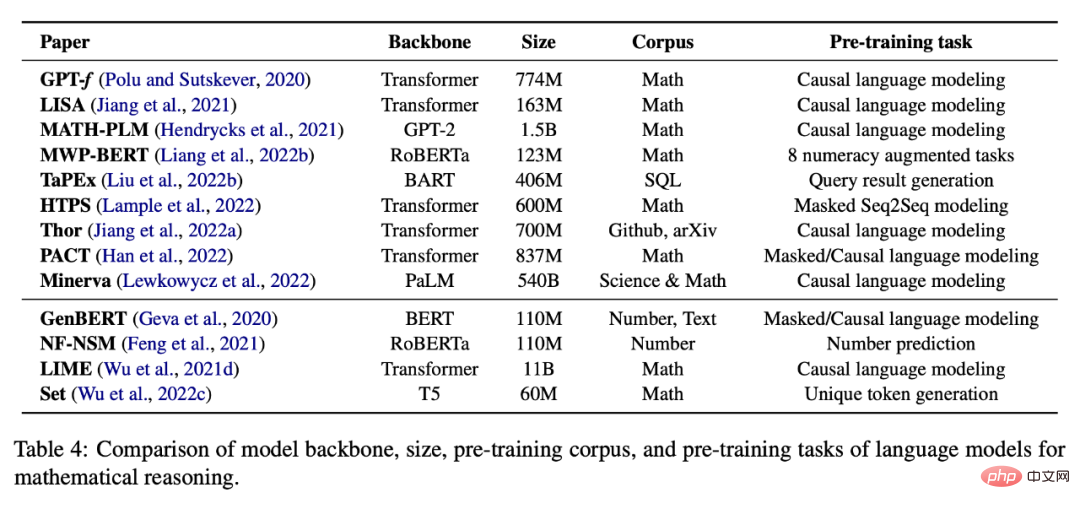
以下の表 4 は、数学の事前トレーニング済み自己教師ありタスクを示しています。推論 言語モデルのリスト。
#タスク固有の数学的微調整
存在しない場合タスク固有の微調整に十分なデータを使用することも、大規模なモデルを最初からトレーニングする場合の一般的な方法です。表 5 に示すように、既存の研究では、さまざまな下流タスクで事前トレーニングされた言語モデルを微調整することが試みられています。
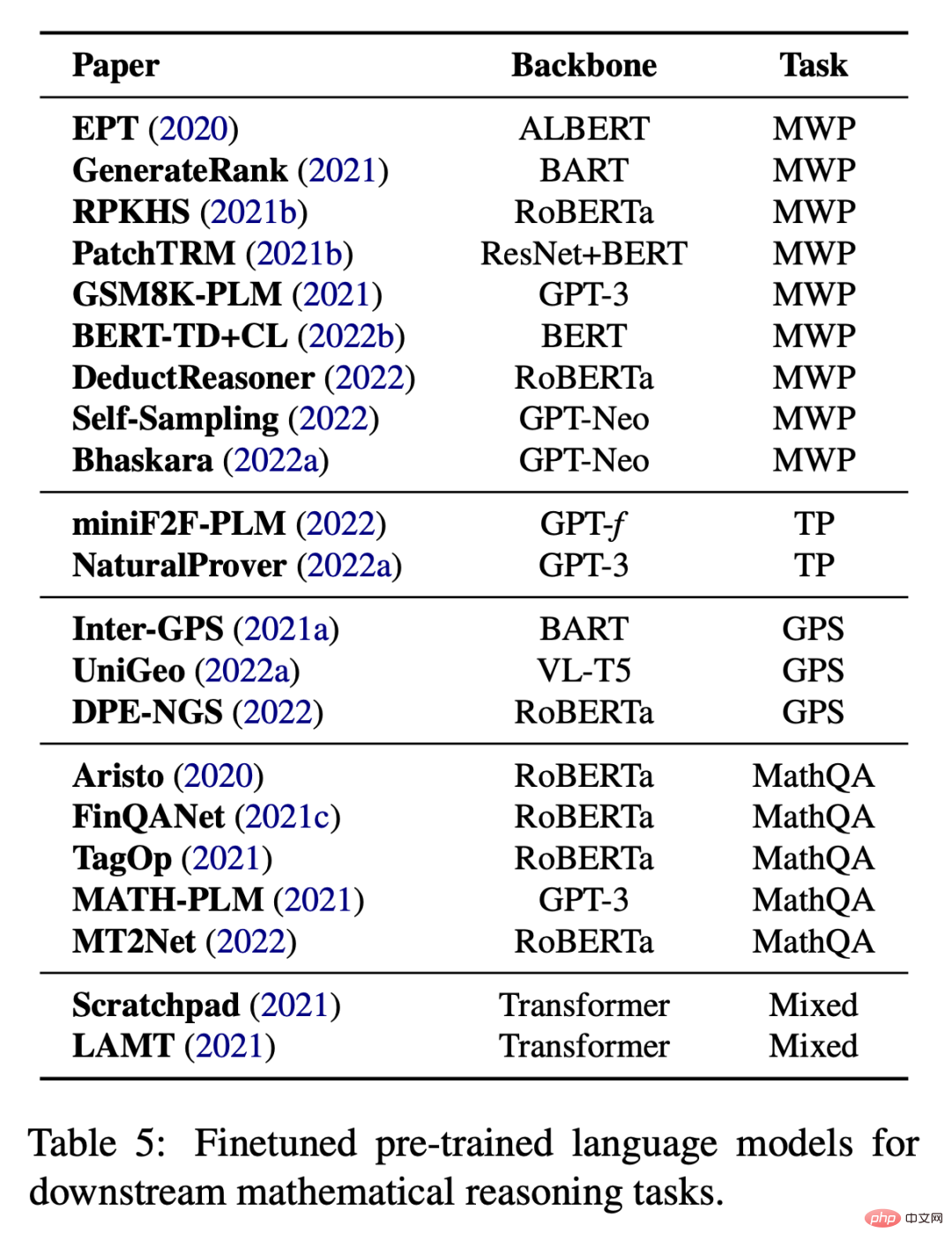
除了對模型參數進行微調,許多工作還使用預訓練語言模型作為編碼器,將其與其他模組組合起來完成下游任務,例如,IconQA 提出將ResNet 和BERT 分別用於圖表識別和文本理解。
數學推理中的上下文學習
一個上下文的樣本通常包含一個輸入- 輸出對和一些prompt 詞,例如,請從列表中選擇最大的數字。
輸入:[2, 4, 1, 5, 8]
輸出:8。
少樣本學習會給出多個樣本,然後模型在最後一個輸入樣本時預測輸出。然而這種標準的少樣本 prompting,即在 test-time 樣本前給大型語言模型提供輸入 - 輸出對的上下文樣本,還沒有被證明足以在數學推理等挑戰性任務上取得良好表現。
思考鏈(Chain-of-thought prompting,CoT)利用中間的自然語言解釋作為 prompt,使大型語言模型首先產生推理鏈,然後預測一個輸入問題的答案。例如,一個解決應用問題的CoT prompt 可以是

Kojima et al.(2022)提出,為模型提供「讓我們一步一步地思考!(Let's think step by step!)」的prompt 會讓大型語言模型成為良好的零樣本推理器。除此之外,近期的大部分工作都集中在如何在零樣本推理的設定下改進思維鏈推理。這類工作主要分為兩部分:(i)選擇更好的上下文樣本和(ii)創造更好的推理鏈。
上下文樣本選擇
#早期的思維鏈工作是隨機或啟發式地選擇上下文樣本。最近的研究表明,在不同的情境例子選擇中,這種類型的少樣本學習可能是非常不穩定的。因此,哪些上下文的推理樣本能做出最有效率的 prompt,在學術上仍是一個未知的問題。
為了解決這個限制,最近的一些工作研究了各種方法來優化上下文樣本的選擇過程。例如,Rubin et al.(2022)試圖透過檢索語意相似的樣本來解決這個問題。然而,這種方法在數學推理問題上效果不佳,而且如果包含結構化資訊(如表格)就很難衡量相似性。此外,Fu et al.(2022)提出了基於複雜性的 prompt,選擇具有複雜推理鏈的樣本(即具有更多推理步驟的鏈)作為 prompt。 Lu et al.(2022b)提出了一種透過強化學習來選擇情境樣本的方法。具體來說,智能體學習從候選池中找到最佳的上下文樣本,目的是在與 GPT-3 環境互動時,使給定的訓練樣本的預測獎勵最大化。此外,Zhang et al.(2022b)發現範例問題的多樣化也可以提高模型效能。他們提出了一個兩步驟法來建構上下文中的範例問題:首先,將給定資料集的問題劃分為幾個群組;其次,從每個群組中選擇一個有代表性的問題,並使用具有簡單啟發式的零樣本思考鏈產生其推理鏈。
高品質推理鏈
#早期的思維鏈工作主要依靠單一的人類註釋推理鏈作為prompt 。然而,人工創建推理鏈有兩個缺點:首先,隨著任務變得越來越複雜,目前的模型可能不足以學會執行所有必要的推理步驟,而且不能輕易推廣到不同的任務;其次,單一的解碼過程很容易受到錯誤推理步驟的影響,導致最終的答案是不正確的預測。為了解決這個限制,最近的研究主要集中在兩個方面:(i)手工製作更複雜的範例,稱為基於過程的方法;(ii)利用類似集合的方法,稱為基於結果的方法。
在評估現有的基準和方法之後,作者也討論了這一領域的未來研究方向。更多研究細節,可參考原論文。
以上が過去 10 年間で論文数が急増していますが、ディープラーニングはどのようにして数学的推論への扉をゆっくりと開いていくのでしょうか?の詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7442
7442
 15
15
 1371
1371
 52
52
 76
76
 11
11
 9
9
 6
6
 Python での感情分析に BERT を使用する方法と手順
Jan 22, 2024 pm 04:24 PM
Python での感情分析に BERT を使用する方法と手順
Jan 22, 2024 pm 04:24 PM
BERT は、2018 年に Google によって提案された事前トレーニング済みの深層学習言語モデルです。正式名は BidirectionEncoderRepresentationsfromTransformers で、Transformer アーキテクチャに基づいており、双方向エンコードの特性を備えています。従来の一方向コーディング モデルと比較して、BERT はテキストを処理するときにコンテキスト情報を同時に考慮できるため、自然言語処理タスクで優れたパフォーマンスを発揮します。その双方向性により、BERT は文内の意味関係をより深く理解できるようになり、それによってモデルの表現能力が向上します。事前トレーニングおよび微調整方法を通じて、BERT は感情分析、命名などのさまざまな自然言語処理タスクに使用できます。
 一般的に使用される AI 活性化関数の分析: Sigmoid、Tanh、ReLU、Softmax のディープラーニングの実践
Dec 28, 2023 pm 11:35 PM
一般的に使用される AI 活性化関数の分析: Sigmoid、Tanh、ReLU、Softmax のディープラーニングの実践
Dec 28, 2023 pm 11:35 PM
活性化関数は深層学習において重要な役割を果たしており、ニューラル ネットワークに非線形特性を導入することで、ネットワークが複雑な入出力関係をより適切に学習し、シミュレートできるようになります。活性化関数の正しい選択と使用は、ニューラル ネットワークのパフォーマンスとトレーニング結果に重要な影響を与えます。この記事では、よく使用される 4 つの活性化関数 (Sigmoid、Tanh、ReLU、Softmax) について、導入、使用シナリオ、利点、欠点と最適化ソリューション アクティベーション関数を包括的に理解できるように、次元について説明します。 1. シグモイド関数 シグモイド関数の公式の概要: シグモイド関数は、任意の実数を 0 と 1 の間にマッピングできる一般的に使用される非線形関数です。通常は統一するために使用されます。
 ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
ORB-SLAM3を超えて! SL-SLAM: 低照度、重度のジッター、弱いテクスチャのシーンはすべて処理されます。
May 30, 2024 am 09:35 AM
以前に書きましたが、今日は、深層学習テクノロジーが複雑な環境におけるビジョンベースの SLAM (同時ローカリゼーションとマッピング) のパフォーマンスをどのように向上させることができるかについて説明します。ここでは、深部特徴抽出と深度マッチング手法を組み合わせることで、低照度条件、動的照明、テクスチャの弱い領域、激しいセックスなどの困難なシナリオでの適応を改善するように設計された多用途のハイブリッド ビジュアル SLAM システムを紹介します。当社のシステムは、拡張単眼、ステレオ、単眼慣性、ステレオ慣性構成を含む複数のモードをサポートしています。さらに、他の研究にインスピレーションを与えるために、ビジュアル SLAM と深層学習手法を組み合わせる方法も分析します。公開データセットと自己サンプリングデータに関する広範な実験を通じて、測位精度と追跡堅牢性の点で SL-SLAM の優位性を実証しました。
 Stable Diffusion 3 の論文がついに公開され、アーキテクチャの詳細が明らかになりましたが、Sora の再現に役立つでしょうか?
Mar 06, 2024 pm 05:34 PM
Stable Diffusion 3 の論文がついに公開され、アーキテクチャの詳細が明らかになりましたが、Sora の再現に役立つでしょうか?
Mar 06, 2024 pm 05:34 PM
StableDiffusion3 の論文がついに登場しました!このモデルは2週間前にリリースされ、Soraと同じDiT(DiffusionTransformer)アーキテクチャを採用しており、リリースされると大きな話題を呼びました。前バージョンと比較して、StableDiffusion3で生成される画像の品質が大幅に向上し、マルチテーマプロンプトに対応したほか、テキスト書き込み効果も向上し、文字化けが発生しなくなりました。 StabilityAI は、StableDiffusion3 はパラメータ サイズが 800M から 8B までの一連のモデルであると指摘しました。このパラメーター範囲は、モデルを多くのポータブル デバイス上で直接実行できることを意味し、AI の使用を大幅に削減します。
 潜在空間の埋め込み: 説明とデモンストレーション
Jan 22, 2024 pm 05:30 PM
潜在空間の埋め込み: 説明とデモンストレーション
Jan 22, 2024 pm 05:30 PM
潜在空間埋め込み (LatentSpaceEmbedding) は、高次元データを低次元空間にマッピングするプロセスです。機械学習と深層学習の分野では、潜在空間埋め込みは通常、高次元の入力データを低次元のベクトル表現のセットにマッピングするニューラル ネットワーク モデルです。このベクトルのセットは、「潜在ベクトル」または「潜在ベクトル」と呼ばれることがよくあります。エンコーディング」。潜在空間埋め込みの目的は、データ内の重要な特徴をキャプチャし、それらをより簡潔でわかりやすい形式で表現することです。潜在空間埋め込みを通じて、低次元空間でデータの視覚化、分類、クラスタリングなどの操作を実行し、データをよりよく理解して活用できます。潜在空間埋め込みは、画像生成、特徴抽出、次元削減など、多くの分野で幅広い用途があります。潜在空間埋め込みがメイン
 1 つの記事で理解: AI、機械学習、ディープラーニングのつながりと違い
Mar 02, 2024 am 11:19 AM
1 つの記事で理解: AI、機械学習、ディープラーニングのつながりと違い
Mar 02, 2024 am 11:19 AM
今日の急速な技術変化の波の中で、人工知能 (AI)、機械学習 (ML)、および深層学習 (DL) は輝かしい星のようなもので、情報技術の新しい波をリードしています。これら 3 つの単語は、さまざまな最先端の議論や実践で頻繁に登場しますが、この分野に慣れていない多くの探検家にとって、その具体的な意味や内部のつながりはまだ謎に包まれているかもしれません。そこで、まずはこの写真を見てみましょう。ディープラーニング、機械学習、人工知能の間には密接な相関関係があり、進歩的な関係があることがわかります。ディープラーニングは機械学習の特定の分野であり、機械学習
 超強い!深層学習アルゴリズムのトップ 10!
Mar 15, 2024 pm 03:46 PM
超強い!深層学習アルゴリズムのトップ 10!
Mar 15, 2024 pm 03:46 PM
2006 年にディープ ラーニングの概念が提案されてから、ほぼ 20 年が経過しました。ディープ ラーニングは、人工知能分野における革命として、多くの影響力のあるアルゴリズムを生み出してきました。では、ディープラーニングのトップ 10 アルゴリズムは何だと思いますか?私の考えでは、ディープ ラーニングのトップ アルゴリズムは次のとおりで、いずれもイノベーション、アプリケーションの価値、影響力の点で重要な位置を占めています。 1. ディープ ニューラル ネットワーク (DNN) の背景: ディープ ニューラル ネットワーク (DNN) は、多層パーセプトロンとも呼ばれ、最も一般的なディープ ラーニング アルゴリズムです。最初に発明されたときは、コンピューティング能力のボトルネックのため疑問視されていました。最近まで長年にわたる計算能力、データの爆発的な増加によって画期的な進歩がもたらされました。 DNN は、複数の隠れ層を含むニューラル ネットワーク モデルです。このモデルでは、各層が入力を次の層に渡し、
 NeRFと自動運転の過去と現在、10本近くの論文をまとめました!
Nov 14, 2023 pm 03:09 PM
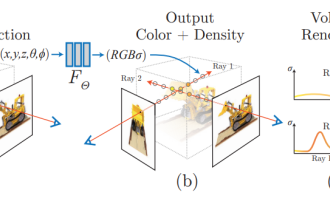
NeRFと自動運転の過去と現在、10本近くの論文をまとめました!
Nov 14, 2023 pm 03:09 PM
Neural Radiance Fieldsは2020年に提案されて以来、関連論文の数が飛躍的に増加し、3次元再構成の重要な分野となっただけでなく、自動運転の重要なツールとして研究の最前線でも徐々に活発になってきています。 NeRF は、過去 2 年間で突然出現しました。その主な理由は、特徴点の抽出とマッチング、エピポーラ幾何学と三角形分割、PnP とバンドル調整、および従来の CV 再構成パイプラインのその他のステップをスキップし、メッシュ再構成、マッピング、ライト トレースさえもスキップするためです。 、2D から直接入力画像を使用して放射線野を学習し、実際の写真に近いレンダリング画像が放射線野から出力されます。言い換えれば、ニューラル ネットワークに基づく暗黙的な 3 次元モデルを指定されたパースペクティブに適合させます。




