Python を使用してトップ 10 の古典的な並べ替えアルゴリズムを実装する

10 の古典的なソート アルゴリズムには、バブル ソート、選択ソート、クイック ソート、マージ ソート、ヒープ ソート、挿入ソート、ヒル ソート、カウンティング ソート、バケット ソート、基数ソートなどが含まれます。
もちろん、他にもいくつかの並べ替えアルゴリズムがあるので、引き続き学習することができます。
01バブル ソート
バブル ソートは比較的単純な並べ替えアルゴリズムです。並べ替え対象の要素を繰り返し訪問し、隣接する 2 つの要素を順番に比較します。順序が間違っている場合は、それらを入れ替えます。要素を交換する必要がなくなり、並べ替えが完了するまで。
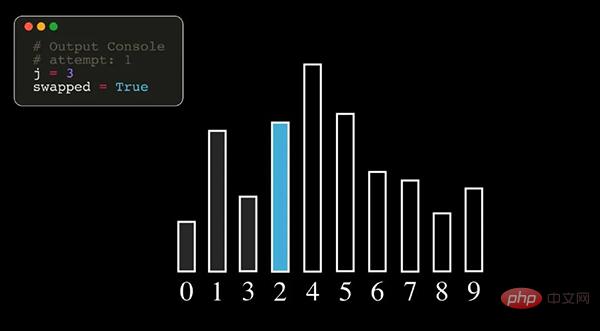
注: 上の図では、数字はデータ シーケンスの元のインデックス番号を表します。
アルゴリズム処理
- 隣接する要素を比較し、前者の方が後者の要素より大きい場合は、位置を入れ替えます。
- すべてが完了するまで、並べ替えられた配列内の隣接する要素の各ペアに対して同じ作業を行います。この時点で、最後の要素がこの並べ替えラウンドの最大の数になります。
- 比較する必要のある要素がなくなるまで、残りの要素に対して上記の手順を繰り返します。
バブル ソートでは毎回最大の要素が見つかるため、n-1 回スキャンする必要があります (n はデータ シーケンスの長さです)。
アルゴリズム機能
最も速い場合 (最良のケース): 入力データがすでに正の順序になっている場合。
最も遅い場合 (最悪のケース): 入力データが逆の順序である場合。
Python コード
def bubble_sort(lst): n = len(lst) for i in range(n): for j in range(1, n - i): if lst[j - 1] > lst[j]: lst[j - 1], lst[j] = lst[j], lst[j - 1] return lst
02 選択ソート
選択ソートの原則
選択ソートの原則、各ラウンドはソート対象のレコードから始まります。シーケンスから最小の要素を取り出してシーケンスの先頭に格納し、その後、ソートされていない残りの要素から最小の要素を見つけて、ソートされたシーケンスの最後に置きます。ソートされるすべてのデータ要素の数がゼロになるまで、同様に続きます。到着値の小さい順にソートしたデータ列を取得します。
各ラウンドで最大値を持つ要素を見つけることもできます。この場合、ソートされた配列は最終的に大きいものから小さいものの順に並べられます。
選択ソートでは毎回最小 (最大) 要素が選択されるため、n-1 回スキャンする必要があります。
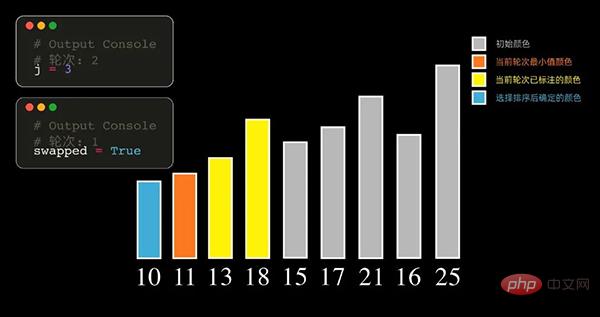
Python コード
def selection_sort(lst): for i in range(len(lst) - 1): min_index = i for j in range(i + 1, len(lst)): if lst[j] < lst[min_index]: min_index = j lst[i], lst[min_index] = lst[min_index], lst[i] return lst
03Quick Sort
Quick Sort (クイック ソート) は、1960 年代にアメリカ人によって開発されたソート手法です。トニー・ホール。このソート方法は、当時すでに非常に高速なソート方法でした。したがって、ネーミング的には「クイックソート」と呼ばれます。
アルゴリズム プロセス
- まず、データ シーケンスからベースライン番号として数値を取得します (ベースライン。最初の数値を取得するのが一般的です)。
- 分割プロセス中、基数より小さいすべての数値が左側に配置され、基数以上のすべての数値が右側に配置されます。
- 各間隔に数値が 1 つだけになるまで、左右の間隔に対して 2 番目のステップを再帰的に繰り返します。
データシーケンス間の順序は固定されているためです。最後に、これらの部分列を一度に結合して、全体の並べ替えが完了します。
下図のように、データ列は最初のデータ15を基数として、15より小さい数値を左側、15より大きい数値(以上)を配置します。 to) on the right
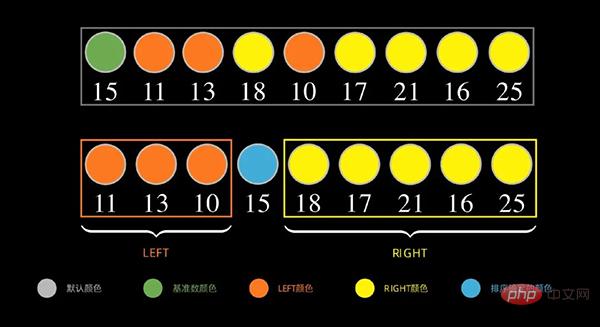
次に、左側の部分について、上記の手順を繰り返します。以下に示すように、左側のシーケンスの最初のデータ 11 をベースとして使用します。 11 より小さい数字は左側に、11 より大きい(以上)数字は右側に配置されます。
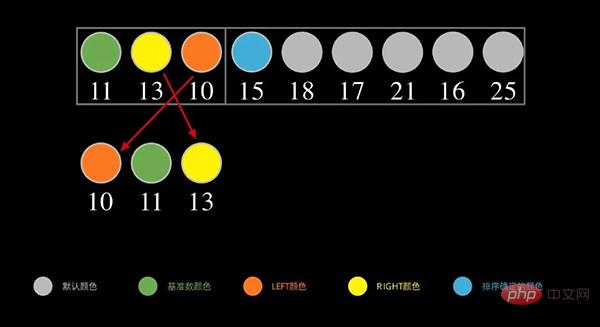
各間隔に数値が 1 つだけになるまで、上記のプロセスを再帰的に繰り返します。これで並べ替えが完了します。
Python コード
def quick_sort(lst): n = len(lst) if n <= 1: return lst baseline = lst[0] left = [lst[i] for i in range(1, len(lst)) if lst[i] < baseline] right = [lst[i] for i in range(1, len(lst)) if lst[i] >= baseline] return quick_sort(left) + [baseline] + quick_sort(right)
04マージ ソート
アルゴリズムのアイデア
マージ ソート (マージ ソート) はマージ操作に基づいています。ソートアルゴリズム。このアルゴリズムは、分割統治法の非常に典型的な応用例であり、マージ ソートは、既に順序付けされた 2 つのサブシーケンスを順序付けられたシーケンスにマージします。
アルゴリズム プロセス
主な 2 つのステップ (分割、マージ)
- ステップ 1: 要素が 1 つだけになるまでシーケンスを分割します。
- ステップ 2: 分割が完了したら、再帰的マージを開始します。
アイデア: ソートされていないシーケンスがあると仮定します。次に、最初に分割メソッドを使用して、シーケンスをソートされたサブシーケンスに分割します (要素が 1 つ残るまで)。次に、merge メソッドを使用して、順序付けされたサブシーケンスを順序付けられたシーケンスにマージします。
グラフィック アルゴリズム
分割
データ シーケンス [15,11,13,18,10] については、まずデータ シーケンスの中間位置から分割を開始します。中間位置は
に設定され、最初の分割は次のようになります:
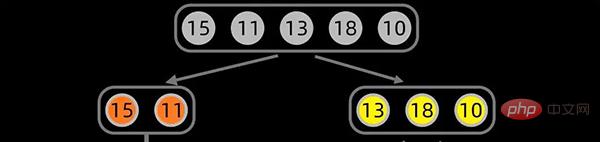
第一次拆分后,依次对子序列进行拆分,拆分过程如下:
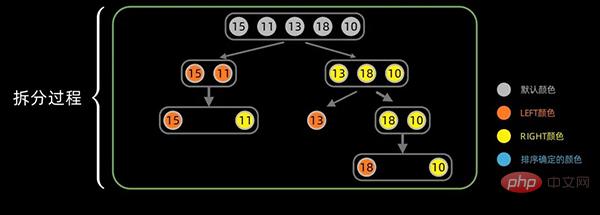
合并
合并过程中,对于左右分区以及其子区间,递归使用合并方法。先从左边最小的子区间开始,对于每个区间,依次将最小的数据放在最左边,然后对右边区间也执行同样的操作。
合并过程的完整图示如下:
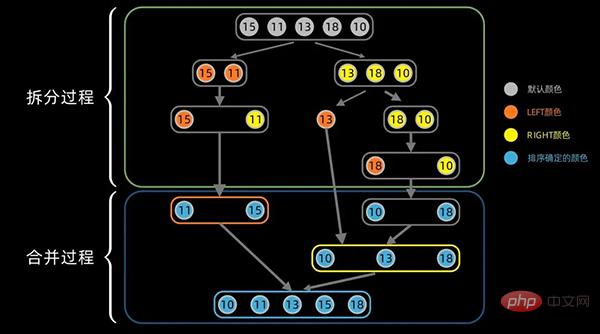
Python代码
def merge_sort(lst): def merge(left,right): i = 0 j = 0 result = [] while i < len(left) and j < len(right): if left[i] <= right[j]: result.append(left[i]) i += 1 else: result.append(right[j]) j += 1 result = result + left[i:] + right[j:] return result n = len(lst) if n <= 1: return lst mid = n // 2 left = merge_sort(lst[:mid]) right = merge_sort(lst[mid:]) return merge(left,right)
05堆排序
要理解堆排序(Heap Sort)算法,首先要知道什么是“堆”。
堆的定义
对于 n 个元素的数据序列
,当且仅当满足下列情形之一时,才称之为 堆:
情形1:
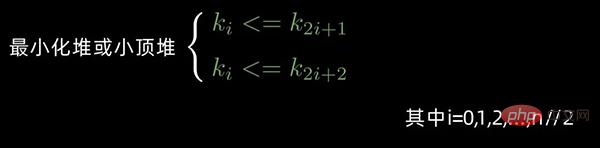
情形2:
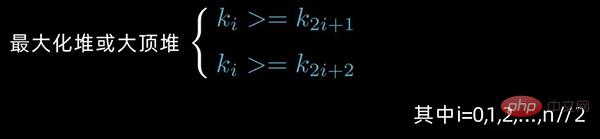
若序列
是堆,则堆顶元素必为序列中n个元素的最小值或最大值。
小顶堆如下图所示:
小顶堆
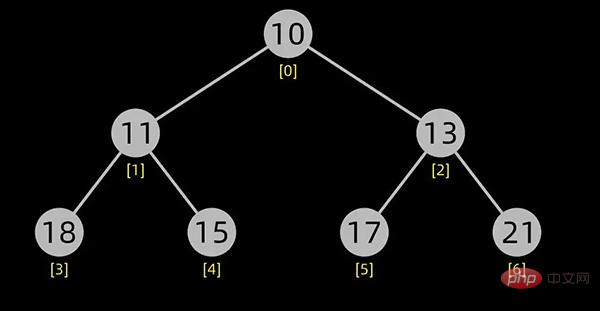
大顶堆如下图所示:
大顶堆
若在输出堆顶的最小值(或最大值)之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素的次小值(或次大值)。如此反复执行,便能得到一个有序序列,这个过程称之为 堆排序。
堆的存储
一般用数组来表示堆,若根结点存在序号 0 处, i 结点的父结点下标就为 (i-1)/2。i 结点的左右子结点下标分别为 2*i+1和 2*i+2 。
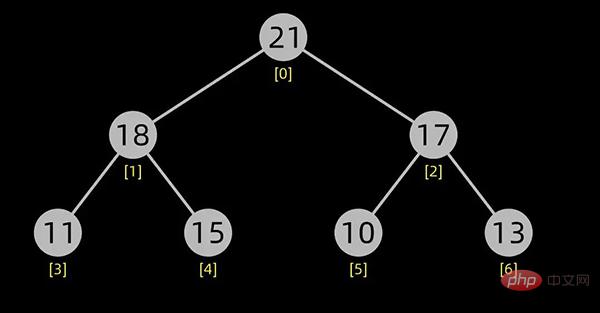
对于上面提到的小顶堆和大顶堆,其数据存储情况如下:
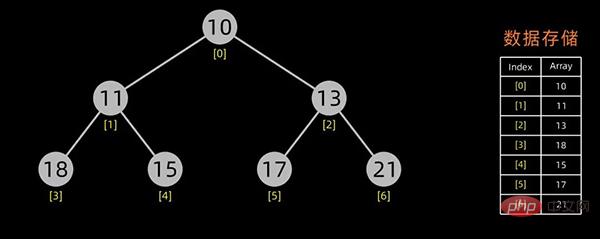
小顶堆
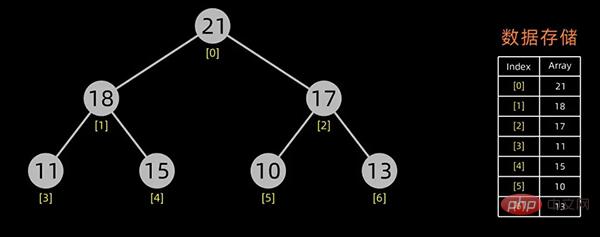
大顶堆
每幅图的右边为其数据存储结构,左边为其逻辑结构。
堆排序
实现堆排序需要解决两个问题:
- 如何由一个无序序列建成一个堆?
- 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
堆的初始化
第一个问题实际上就是堆的初始化,下面来阐述下如何构造初始堆,假设初始的数据序列如下:

咱们首先需要将其以树形结构来展示,如下:
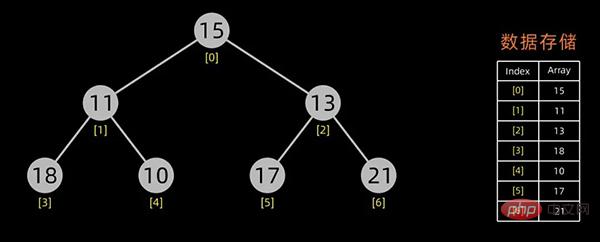
初始化堆的时候是对所有的非叶子结点进行筛选。
最后一个非终端元素的下标是 [n/2] 向下取整,所以筛选只需要从第 [n/2] 向下取整个元素开始,从后往前进行调整。
从最后一个非叶子结点开始,每次都是从父结点、左边子节点、右边子节点中进行比较交换,交换可能会引起子结点不满足堆的性质,所以每次交换之后需要重新对被交换的子结点进行调整。
以小顶堆为例,构造初始堆的过程如下:
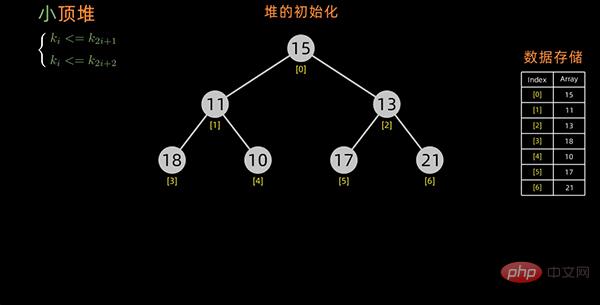
进行堆排序
有了初始堆之后就可以进行排序了。
堆排序是一种选择排序。建立的初始堆为初始的无序区。
排序开始,首先输出堆顶元素(因为它是最值),将堆顶元素和最后一个元素交换,这样,第n个位置(即最后一个位置)作为有序区,前n-1个位置仍是无序区,对无序区进行调整,得到堆之后,再交换堆顶和最后一个元素,这样有序区长度变为2。。。
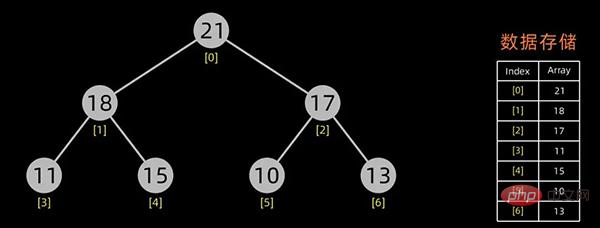
大顶堆
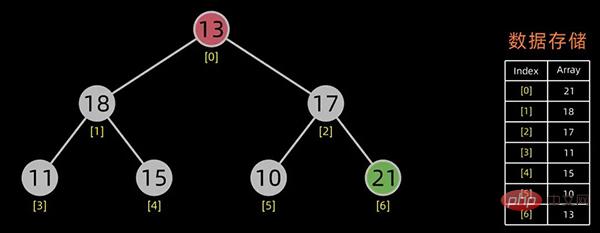
交换堆顶元素和最后的元素
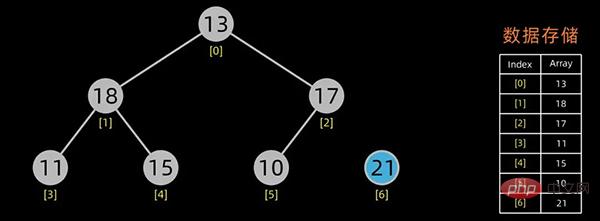
无序区-1,有序区+1
不断进行此操作,将剩下的元素重新调整为堆,然后输出堆顶元素到有序区。每次交换都导致无序区-1,有序区+1。不断重复此过程直到有序区长度增长为n-1,排序完成。
Python代码
def heap_sort(lst): def adjust_heap(lst, i, size): left_index = 2 * i + 1 right_index = 2 * i + 2 largest_index = i if left_index < size and lst[left_index] > lst[largest_index]: largest_index = left_index if right_index < size and lst[right_index] > lst[largest_index]: largest_index = right_index if largest_index != i: lst[largest_index], lst[i] = lst[i], lst[largest_index] adjust_heap(lst, largest_index, size) def built_heap(lst, size): for i in range(len(lst)//2)[::-1]: adjust_heap(lst, i, size) size = len(lst) built_heap(lst, size) for i in range(len(lst))[::-1]: lst[0], lst[i] = lst[i], lst[0] adjust_heap(lst, 0, i) return lst
06插入排序
插入排序(Insertion Sort)就是每一步都将一个需要排序的数据按其大小插入到已经排序的数据序列中的适当位置,直到全部插入完毕。
插入排序如同打扑克牌一样,每次将后面的牌插到前面已经排好序的牌中。

Python代码
def insertion_sort(lst): for i in range(len(lst) - 1): cur_num, pre_index = lst[i+1], i while pre_index >= 0 and cur_num < lst[pre_index]: lst[pre_index + 1] = lst[pre_index] pre_index -= 1 lst[pre_index + 1] = cur_num return lst
07希尔排序
基本原理
希尔排序(Shell Sort)是插入排序的一种更高效率的实现。
希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列,也可以动态的定义间隔序列。
这里以动态间隔序列为例来描述。初始间隔(gap值)为数据序列长度除以2取整,后续间隔以 前一个间隔数值除以2取整为循环,直到最后一个间隔值为 1 。
对于下面这个数据序列,初始间隔数值为5
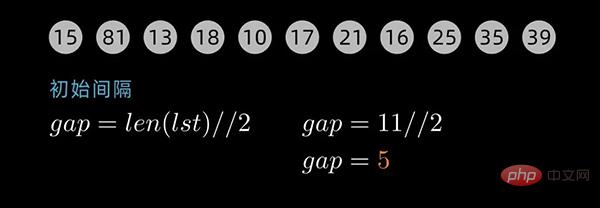
先将数据序列按间隔进行子序列分组,第一个子序列的索引为[0,5,10],这里分成了5组。

为方便大家区分不同的子序列,对同一个子序列标注相同的颜色,分组情况如下:
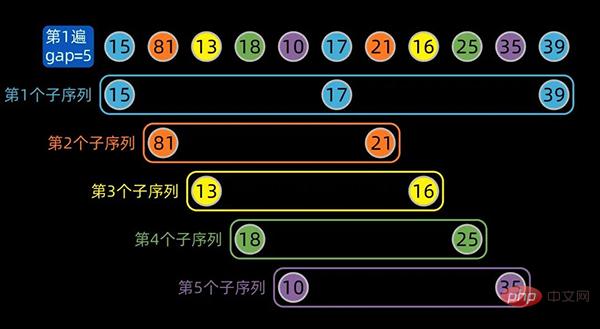
分组结束后,子序列内部进行插入排序,gap为5的子序列内部排序后如下:
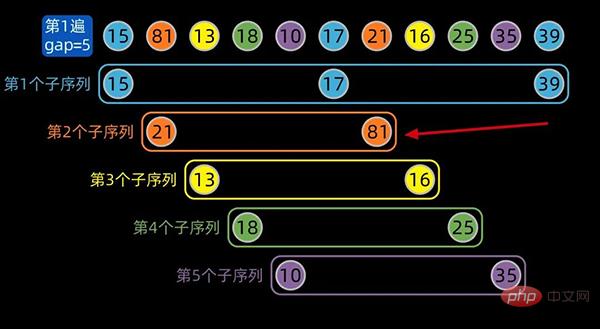

注:红色箭头标注的地方,是子序列内部排序后的状态
接下来选取第二个间隔值,按照间隔值进行子序列分组,同样地,子序列内部分别进行插入排序;
如果数据序列比较长,则会选取第3个、第4个或者更多个间隔值,重复上述的步骤。
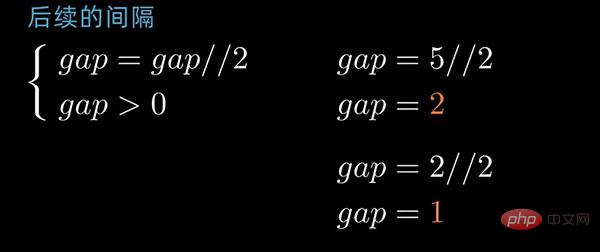
gap为2的排序情况前后对照如下:

最后一个间隔值为1,这一次相当于简单的插入排序。但是经过前几次排序,序列已经基本有序,因此最后一次排序时间效率就提高了很多。

Python代码
def shell_sort(lst): n = len(lst) gap = n // 2 while gap > 0: for i in range(gap, n): for j in range(i, gap - 1, -gap): if lst[j] < lst[j - gap]: lst[j], lst[j - gap] = lst[j - gap], lst[j] else: break gap //= 2 return lst
08计数排序
基本原理
计数排序(Counting Sort)的核心在于将输入的数据值转化为键,存储在额外开辟的数组空间中。计数排序要求输入的数据必须是有确定范围的整数。
算法的步骤如下:
先找出待排序的数组中最大和最小的元素,新开辟一个长度为 最大值-最小值+1 的数组;
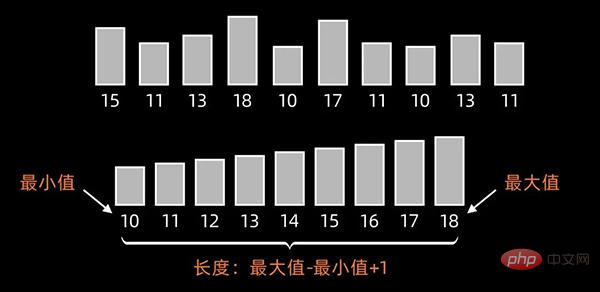
然后,统计原数组中每个元素出现的次数,存入到新开辟的数组中;
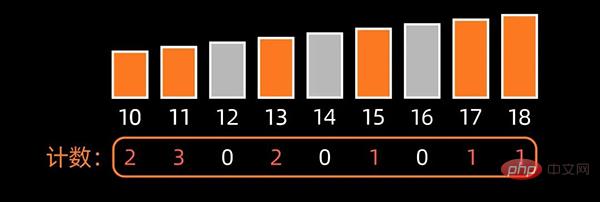
接下来,根据每个元素出现的次数,按照新开辟数组中从小到大的秩序,依次填充到原来待排序的数组中,完成排序。
Python代码
def counting_sort(lst): nums_min = min(lst) bucket = [0] * (max(lst) + 1 - nums_min) for num in lst: bucket[num - nums_min] += 1 i = 0 for j in range(len(bucket)): while bucket[j] > 0: lst[i] = j + nums_min bucket[j] -= 1 i += 1 return lst
09桶排序
基本思想
简单来说,桶排序(Bucket Sort)就是把数据分组,放在一个个的桶中,对每个桶里面的数据进行排序,然后将桶进行数据合并,完成桶排序。
该算法分为四步,包括划分桶、数据入桶、桶内排序、数据合并。
桶的划分过程
这里详细介绍下桶的划分过程。
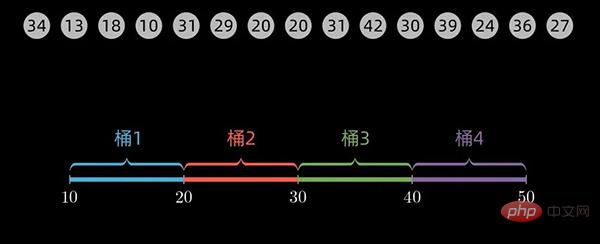
对于一个数值范围在10到 49范围内的数组,我们取桶的大小为10 (defaultBucketSize = 10),则第一个桶的范围为 10到20,第二个桶的数据范围是20到30,依次类推。最后,我们一共需要4个桶来放入数据。

排序过程
对于下面这个数据序列,初始设定桶的大小为 20 (defaultBucketSize = 20),经计算,一共需要4个桶来放入数据。
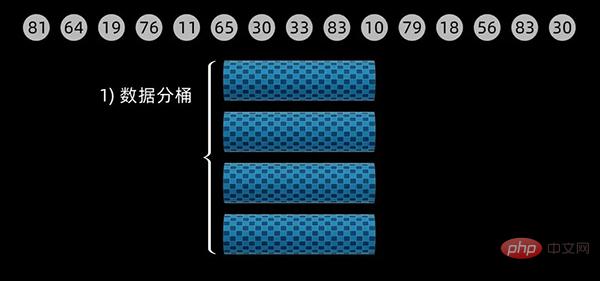
然后将原始数组按数值大小放入到对应的桶中,完成数据分组。
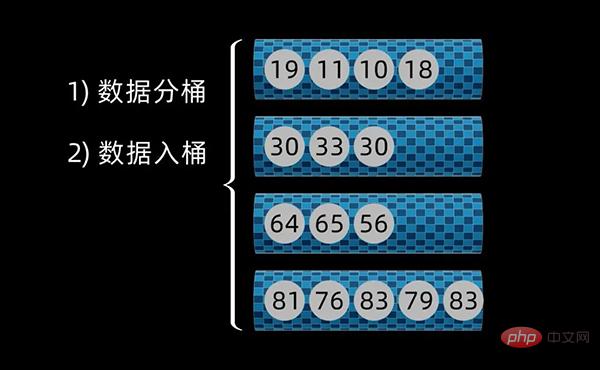
对于桶内的数据序列,这时可以用冒泡排序、选择排序等多种排序算法来对数据进行排序。这些算法,在之前的视频里已有介绍,大家可以去了解下。
这里,我选用 冒泡排序 来对桶内数据进行排序。
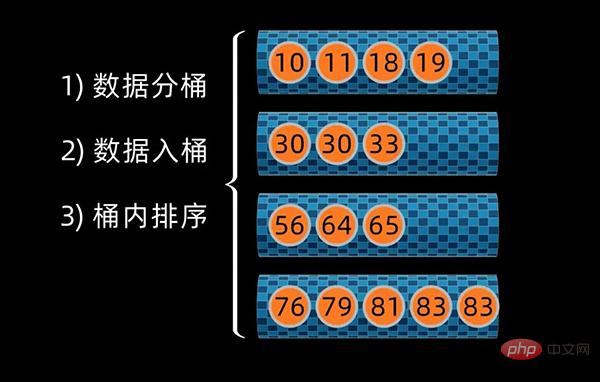
桶内排序完成后,将数据按桶的顺序进行合并,这样就得到所有数值排好序的数据序列了

Python代码
def bucket_sort(lst, defaultBucketSize=4): maxVal, minVal = max(lst), min(lst) bucketSize = defaultBucketSize bucketCount = (maxVal - minVal) // bucketSize + 1 buckets = [[] for i in range(bucketCount)] for num in lst: buckets[(num - minVal) // bucketSize].append(num) lst.clear() for bucket in buckets: bubble_sort(bucket) lst.extend(bucket) return lst
10基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),它是透过键值的部份信息,将要排序的元素分配至某些“桶”中,以达到排序的作用。
基数排序适用于所有元素均为正整数的数组。
基本思想
排序过程分为“分配”和“收集”。
排序过程中,将元素分层为多个关键码进行排序(一般按照数值的个位、十位、百位、…… 进行区分),多关键码排序按照从最主位关键码到最次位关键码或从最次位到最主位关键码的顺序逐次排序。
基数排序的方式可以采用最低位优先LSD(Least sgnificant digital)法或最高位优先MSD(Most sgnificant digital)法,LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好,MSD的方式恰与LSD相反,是由高位数为基底开始进行分配,其他的演算方式则都相同。
算法流程
这里以最低位优先LSD为例。
先根据个位数的数值,在扫描数值时将它们分配至编号0到9的桶中,然后将桶子中的数值串接起来。
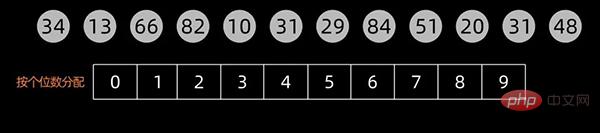
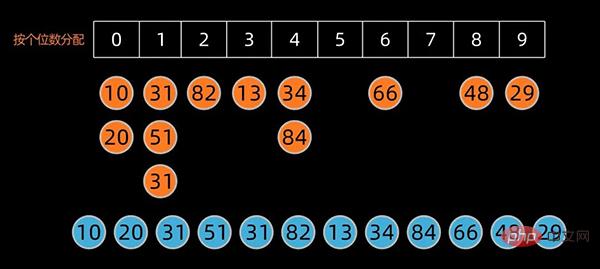
将这些桶子中的数值重新串接起来,成为新的序列,接着再进行一次分配,这次是根据十位数来分配。

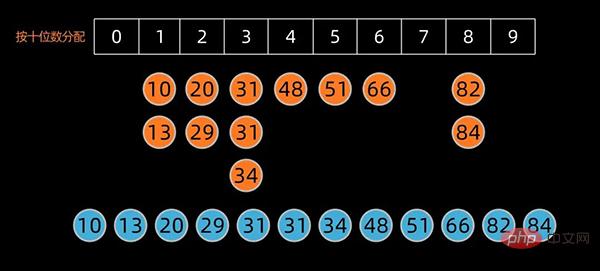
如果排序的对象有三位数以上,则持续进行以上的动作直至最高位数为止。
Python代码
# LSD Radix Sort def radix_sort(lst): mod = 10 div = 1 mostBit = len(str(max(lst))) buckets = [[] for row in range(mod)] while mostBit: for num in lst: buckets[num // div % mod].append(num) i = 0 for bucket in buckets: while bucket: lst[i] = bucket.pop(0) i += 1 div *= 10 mostBit -= 1 return lst
11小结
以上就是用 Python 来实现10种经典排序算法的相关内容。
对于这些排序算法的实现,代码其实并不是最主要的,重要的是需要去理解各种算法的基本思想、基本原理以及其内部的实现过程。
对于每种算法,用其他编程语言同样是可以去实现的。
并且,对于同一种算法,即使只用 Python 语言,也有多种不同的代码方式可以来实现,但其基本原理是一致的。
以上がPython を使用してトップ 10 の古典的な並べ替えアルゴリズムを実装するの詳細内容です。詳細については、PHP 中国語 Web サイトの他の関連記事を参照してください。

ホットAIツール

Undresser.AI Undress
リアルなヌード写真を作成する AI 搭載アプリ

AI Clothes Remover
写真から衣服を削除するオンライン AI ツール。

Undress AI Tool
脱衣画像を無料で

Clothoff.io
AI衣類リムーバー

AI Hentai Generator
AIヘンタイを無料で生成します。

人気の記事

ホットツール

メモ帳++7.3.1
使いやすく無料のコードエディター

SublimeText3 中国語版
中国語版、とても使いやすい

ゼンドスタジオ 13.0.1
強力な PHP 統合開発環境

ドリームウィーバー CS6
ビジュアル Web 開発ツール

SublimeText3 Mac版
神レベルのコード編集ソフト(SublimeText3)

ホットトピック
 7563
7563
 15
15
 1385
1385
 52
52
 84
84
 11
11
 28
28
 99
99
 PHPおよびPython:コードの例と比較
Apr 15, 2025 am 12:07 AM
PHPおよびPython:コードの例と比較
Apr 15, 2025 am 12:07 AM
PHPとPythonには独自の利点と短所があり、選択はプロジェクトのニーズと個人的な好みに依存します。 1.PHPは、大規模なWebアプリケーションの迅速な開発とメンテナンスに適しています。 2。Pythonは、データサイエンスと機械学習の分野を支配しています。
 Python vs. JavaScript:コミュニティ、ライブラリ、リソース
Apr 15, 2025 am 12:16 AM
Python vs. JavaScript:コミュニティ、ライブラリ、リソース
Apr 15, 2025 am 12:16 AM
PythonとJavaScriptには、コミュニティ、ライブラリ、リソースの観点から、独自の利点と短所があります。 1)Pythonコミュニティはフレンドリーで初心者に適していますが、フロントエンドの開発リソースはJavaScriptほど豊富ではありません。 2)Pythonはデータサイエンスおよび機械学習ライブラリで強力ですが、JavaScriptはフロントエンド開発ライブラリとフレームワークで優れています。 3)どちらも豊富な学習リソースを持っていますが、Pythonは公式文書から始めるのに適していますが、JavaScriptはMDNWebDocsにより優れています。選択は、プロジェクトのニーズと個人的な関心に基づいている必要があります。
 Dockerの原則の詳細な説明
Apr 14, 2025 pm 11:57 PM
Dockerの原則の詳細な説明
Apr 14, 2025 pm 11:57 PM
DockerはLinuxカーネル機能を使用して、効率的で孤立したアプリケーションランニング環境を提供します。その作業原則は次のとおりです。1。ミラーは、アプリケーションを実行するために必要なすべてを含む読み取り専用テンプレートとして使用されます。 2。ユニオンファイルシステム(UnionFS)は、違いを保存するだけで、スペースを節約し、高速化する複数のファイルシステムをスタックします。 3.デーモンはミラーとコンテナを管理し、クライアントはそれらをインタラクションに使用します。 4。名前空間とcgroupsは、コンテナの分離とリソースの制限を実装します。 5.複数のネットワークモードは、コンテナの相互接続をサポートします。これらのコア概念を理解することによってのみ、Dockerをよりよく利用できます。
 ターミナルVSCODEでプログラムを実行する方法
Apr 15, 2025 pm 06:42 PM
ターミナルVSCODEでプログラムを実行する方法
Apr 15, 2025 pm 06:42 PM
VSコードでは、次の手順を通じて端末でプログラムを実行できます。コードを準備し、統合端子を開き、コードディレクトリが端末作業ディレクトリと一致していることを確認します。プログラミング言語(pythonのpython your_file_name.pyなど)に従って実行コマンドを選択して、それが正常に実行されるかどうかを確認し、エラーを解決します。デバッガーを使用して、デバッグ効率を向上させます。
 Python:自動化、スクリプト、およびタスク管理
Apr 16, 2025 am 12:14 AM
Python:自動化、スクリプト、およびタスク管理
Apr 16, 2025 am 12:14 AM
Pythonは、自動化、スクリプト、およびタスク管理に優れています。 1)自動化:OSやShutilなどの標準ライブラリを介してファイルバックアップが実現されます。 2)スクリプトの書き込み:Psutilライブラリを使用してシステムリソースを監視します。 3)タスク管理:スケジュールライブラリを使用してタスクをスケジュールします。 Pythonの使いやすさと豊富なライブラリサポートにより、これらの分野で優先ツールになります。
 VSCODE拡張機能は悪意がありますか?
Apr 15, 2025 pm 07:57 PM
VSCODE拡張機能は悪意がありますか?
Apr 15, 2025 pm 07:57 PM
VSコード拡張機能は、悪意のあるコードの隠れ、脆弱性の活用、合法的な拡張機能としての自慰行為など、悪意のあるリスクを引き起こします。悪意のある拡張機能を識別する方法には、パブリッシャーのチェック、コメントの読み取り、コードのチェック、およびインストールに注意してください。セキュリティ対策には、セキュリティ認識、良好な習慣、定期的な更新、ウイルス対策ソフトウェアも含まれます。
 vscodeとは何ですか?vscodeとは何ですか?
Apr 15, 2025 pm 06:45 PM
vscodeとは何ですか?vscodeとは何ですか?
Apr 15, 2025 pm 06:45 PM
VSコードは、Microsoftが開発した無料のオープンソースクロスプラットフォームコードエディターと開発環境であるフルネームVisual Studioコードです。幅広いプログラミング言語をサポートし、構文の強調表示、コード自動完了、コードスニペット、および開発効率を向上させるスマートプロンプトを提供します。リッチな拡張エコシステムを通じて、ユーザーは、デバッガー、コードフォーマットツール、GIT統合など、特定のニーズや言語に拡張機能を追加できます。 VSコードには、コードのバグをすばやく見つけて解決するのに役立つ直感的なデバッガーも含まれています。
 NginxをCentosにインストールする方法
Apr 14, 2025 pm 08:06 PM
NginxをCentosにインストールする方法
Apr 14, 2025 pm 08:06 PM
NGINXのインストールをインストールするには、次の手順に従う必要があります。開発ツール、PCRE-Devel、OpenSSL-Develなどの依存関係のインストール。 nginxソースコードパッケージをダウンロードし、それを解凍してコンパイルしてインストールし、/usr/local/nginxとしてインストールパスを指定します。 nginxユーザーとユーザーグループを作成し、アクセス許可を設定します。構成ファイルnginx.confを変更し、リスニングポートとドメイン名/IPアドレスを構成します。 nginxサービスを開始します。依存関係の問題、ポート競合、構成ファイルエラーなど、一般的なエラーに注意する必要があります。パフォーマンスの最適化は、キャッシュをオンにしたり、ワーカープロセスの数を調整するなど、特定の状況に応じて調整する必要があります。




